模型化解题研究
2022-03-16广西南宁市三美学校530021
广西南宁市三美学校(530021) 甘 磊
初三学生数学知识的积累已经比较丰富,且经过三年的解题训练,解题能力也有明显提高。但是,在解答一些知识点比较多,考查综合能力,尤其是函数与几何结合的题目时,他们依然觉得有困难。有的教师为讲解这种“大型”题目,在课堂上耗费时间。更糟糕的是,学生重复训练此类题目,教师也多次重复讲解,教学效果却并不尽如人意。
为了解决这一问题,笔者站在学生“学”的角度去思考,总结出解答此类题目的策略,归纳出此类题目的数学模型。这样,学生在遇到类似的问题时,就可以遵循一定的规律去解决,从而提高解题的效率。
[例1]如图1,在平面直角坐标系中,抛物线与x轴相交于点A(4,0)、B(-2,0),与y轴交于点C(0,-4),AC与抛物线的对称轴相交于点D。
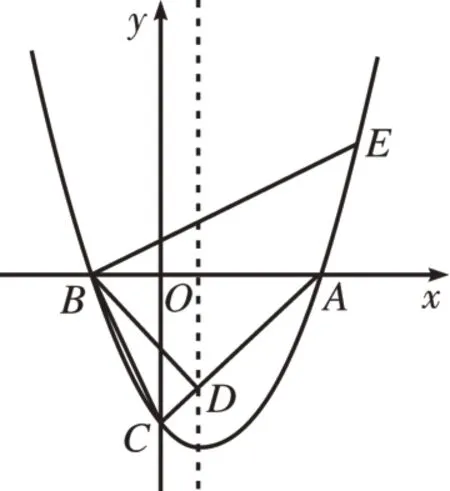
图1
(1)求该抛物线的表达式,并写出点D的坐标;
(2)过点B作BE⊥BC交抛物线于点E,求点E的坐标;
(3)在(2)的条件下,点F在射线BE上,若△ABC∽△DFB,求点F的坐标。
解析:
(1)此问考查二次函数的解析式求法,通过联立方程组可得抛物线的表达式为y=得D(1,-3)。因为这不是本文的重点,所以具体过程省略。
(2)此问增加的条件是两条线的垂直关系,而题目要求点坐标的值,从而易联想到点坐标的值可转换成垂线段长度。而转换的关键是通过三角形相似或者三角函数。过程如下:
如图2,过点E作EH⊥x轴,垂足为H。设E(x,y),

图2

相关解题思路和基本模型可以通过如下示意图来体现。

(3)增加的条件是点的坐标以及相似三角形,依然是求点的坐标,同样容易联想到通过求点与x轴(或y轴)的垂线段长度,从而转换成点坐标的值。解题思路跟(2)差不多,但是比(2)难的地方是,反过来利用了点坐标的值,转换成垂线段长度,再用三角函数得到角度,从而确定F点的位置。过程如下:
如图3,∵△ABC∽△DFB,

图3
∴∠BDF=∠BAC=45°,
∴点F在抛物线的对称轴上。

∵抛物线的对称轴为x=1,

相关解题思路和基本模型可以通过如下示意图来体现。

解题总结:
已知点的坐标,可以通过把坐标值转换成线段长度,从而可以运用几何图形的性质,并通过三角函数或者相似三角形将线段的数量关系找出来,用解方程来求出线段的长度,从而得到点的坐标。也就是说,解决此类问题,可以遵循以下思考步骤。
(1)确定已知了哪些点坐标,它们可以转换成哪些线段的长度;
(2)明确有什么样的几何图形,这些图形有什么特性;
(3)利用相似三角形或者三角函数得到“数与形”的关系;
(4)建立求解的方程;
(5)把线段长度转换成点坐标。
[例2]如图4,已知抛物线y=+bx+c经过A,B,C三个点,其中点A(9,10),点B(0,1),BC∥x轴,点P是直线BC下方抛物线上的动点。

图4
(1)求抛物线的解析式;
(2)过点P且与y轴平行的直线l与直线AB、BC分别交于点E、F,当四边形BECP的面积最大时,求点P的坐标和四边形BECP的最大面积;
(3)当点P为抛物线的顶点时,在直线BC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由。
本题的第(3)小问与本文阐述的观点相关,所以笔者重点讲解第(3)小问。解题的思路基本遵循文中阐述的解答此类题目的规律:通过点坐标转换成线段长度,并利用三角函数找到相等的角,从而确定相似三角形的对应关系,建立方程,得到线段长度再转换成点的坐标。
解:(1)∵点A(9,10),B(0,1)在抛物线上,

(2)∵BC∥x轴,B(0,1),∴-2x+1=1,解得x1=6,x2=0(舍去),∴点C的坐标(6,1),∵点A(9,10),B(0,1),∴直线AB的解析式为y=x+1。

[例3]如图5,在平面直角坐标系xOy中,已知抛物线y=+bx+c与x轴 交于点B(-2,0)和点A,与y轴交于点C(0,-3),经过点B的射线与y轴相交于点E,与抛物线的另一个交点为F,且。
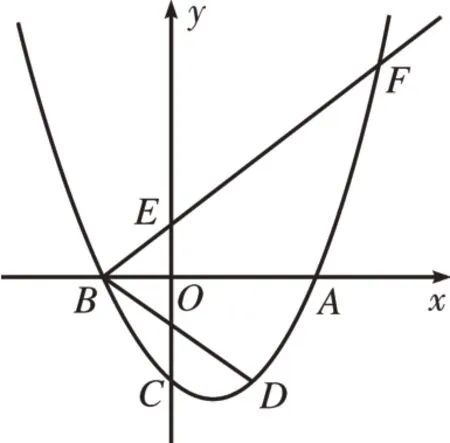
图5
(1)求这条抛物线的解析式,并写出抛物线的对称轴;
(2)求∠FBA的余切值;
(3)点D是点C关于抛物线对称轴的对称点,点P是y轴上一点,且∠BFP=∠DBA,求点P的坐标。
解:(1)把C(0,-3)代入得c=-3,∴抛物线的解析式为y=

(2)如图6,过点F作FM⊥x轴,垂足为M。


图6

(3)∵抛物线的对称轴为x=1,C(0,-3),点D是点C关于抛物线对称轴的对称点,
∴D(2,-3),∴cot∠DBA=,∴∠FBA=∠DBA。
如图7 所示,当点P在BF的上方时,∠PFB=∠DBA=∠FBA,∴PF∥AB,∴yp=yF=6。

图7
由(2)可知F(6,4k),∴F(6,6),点P的坐标为(0,6)。
如图8所示,当点P在BF的下方时,

图8
设FP与x轴的交点为G(h,0),则∠PFB=∠FBA,可得到FG=BG,∴(6-h)2+62=(h+2)2,解 得。
设PF的解析式为y=kx+b,将点F和点G的坐标代入得

综上所述,点P的坐标为(0,6)或。
[例4]如图9,在直角坐标平面内,直线y=分别与x轴、y轴交于点B、C。抛物线bx+c过点C,与x轴交点为点A、B。点D在该抛物线上,且位于直线BC的上方。

图9
(1)求上述抛物线的表达式;
(2)连接AC、AD,且AD交BC于点E,如果△ABE的面积与△ABC的面积之比为4∶5,求∠DBA的余切值;
(3)过点D作DF⊥BC,垂足为点F,连接CD。若△CFD与△AOC相似,求点D的坐标。

∴抛物线的解析式为y=
(2)过点E作EH⊥AB于点H,如图10所示,

图10
当y=0时,-2=0,解得x1=-4(舍去),x2=1,则A(1,0)。


在Rt△AHE中,cot∠EAH=即。
(3)∠BOC=∠DFC=90°。若∠DCF=∠BCO,△DCF∽△BCO,如图11,过点D作DG⊥y轴于点G,过点C作CQ⊥DC交x轴于点Q,∵∠DCQ=∠BOC=90°,∴∠DCF+∠BCQ=90°,即∠BCO+∠BCQ=90°,而∠BCO+∠CBO=90°,∴∠BCQ=∠CBO,∴QB=QC,

图11
设Q(t,0),则t+4=,解得,


整理得8k2-3k=0,解得k1=0(舍去),k2=
如图12,若∠DCF=∠CBO,△DCF∽△CBO,则CD∥BO,∴点D的纵坐标为2,

图12
把y=2 代入y=--得+2=2,解得x1=-3,x2=0(舍去),∴D(-3,2)。
综上所述,点D的坐标为或(-3,2)。
综上可知,题目是千变万化的,我们在讲解题目的过程中,要引导学生去寻找数学模型,并进行归类,使学生慢慢会总结出解题的基本思路,进而顺利解决问题。
