打造“探究和分享”数学课堂——以“与二次函数模型有关的最值问题”教学为例

江苏苏州市平江中学校（215000） 范月娥

培养学生的创新意识，促进学生形成主动探究知识的能力，是初中数学课堂教学改革的重要任务。为此，教师要积极创造宽松的教学环境，以数学问题为载体，引导学生独立思考、主动探究与交流分享，努力把数学课堂打造成“探究和分享”空间。

本文通过“与二次函数模型有关的最值问题”这一课例，阐明培养学生的创新意识，需要教师精心选择教学素材，给学生设置诸如“开放型问题”“变式题”等富有挑战性和探究价值的数学问题，让学生从多个角度探究和解决问题，深刻认识数学知识之间的逻辑关系，积累数学活动经验，掌握数学思想方法，发展发散性思维。

一、基本情况

“与二次函数模型有关的最值问题”一课安排在初三下学期第一轮总复习，是二次函数复习课的第四课时。

授课班级学生数学功底较为扎实，学习主动性强，乐于研究数学问题，乐于分享自己的研究成果。在解决问题时，学生喜欢从不同的角度进行思考，经常会有多种不同的解法产生，学生的发散性思维能力和创新意识较强。

二、教学过程

教学环节一：题目引入

1.用一根长度为20 m 的绳子围成一个矩形，则这个矩形面积的最大值为________。

【变式】若矩形一边靠墙，墙长8 m，则长度为20 m的绳子可以围成的矩形的面积最大值是多少？

2.如图1，在平面直角坐标系中，点A从点M(0,5)出发向原点O匀速运动，与此同时，点B从点N(3,0)出发，在x轴正半轴上以相同的速度向右运动，当点A到达原点O时，两点同时停止运动。连接AB，以线段AB为一边在第一象限内作正方形ABCD，则正方形ABCD面积的最小值为_________。

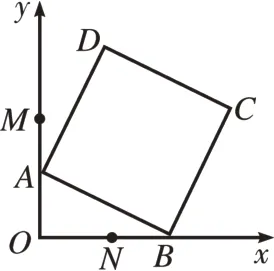
图1

3.如图2，已知半径为2 的⊙O与直线l相切于点A，点P是直径AB左侧半圆上的动点，过点P作直线l的垂线，垂足为C，PC与⊙O交于点D，连接PA、PB，设PC的长为x(2 ＜x＜4)。当x为______时，PD·CD的值最大？

图2

4.如图3，直线l与半径为4 的⊙O相切于点A，P是⊙O上的一个动点（不与点A重合），过点P作PB⊥l，垂足为B，连接PA。设PA=x，PB=y，则(x-y)的最大值是 。

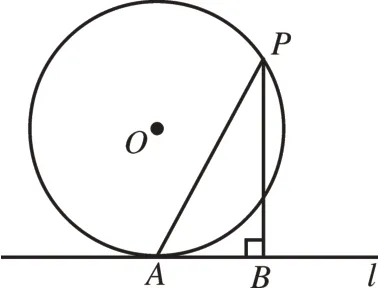
图3

设计意图：通过上述4 道题目，分别引出解决与二次函数模型有关的最值问题的几种常用方法，即公式（面积）、勾股定理、直接表示（构造矩形、全等、坐标等）以及相似三角形（三角函数）。其中第1 题承上启下，回顾了之前复习的二次函数在区间范围内的最值问题，引出了本节课的内容；第2、第3、第4 题分别从需要引入变量、有一个变量和有两个变量这三个角度出发引出本节课的内容。借助这4 道题目，学生可以回忆常用方法，为后续例题的研究奠定良好的基础。

课堂概况：学生对区间范围内的二次函数最值问题非常熟悉，解决起来驾轻就熟，同时对需要引入变量及通过寻找两个变量之间的关系进行消元的思想方法也掌握较好。特别是第3 题引起了学生极大的兴趣，他们分别从以下几个角度展开思考。①看到要表示弦PD，想到添加弦心距，利用垂径定理；②看到两个垂直，想到构造矩形，不仅可以过O作垂线，还可以过P作垂线；③看到PC和AB平行，想到圆中自带等腰，会有角平分线，于是连接PO并延长交圆于一点，构造三角形全等；④通过两对三角形分别相似寻找线段之间的关系，因为是相似直角三角形，所以也可以用三角函数来解答此题。

课后思考：这个环节用时过长，需要进一步精选题目，为后面的教学环节留足时间。学生已经完全掌握且可以轻松解决的第1 题是不是可以省略不讲？题目中没有变量的时候，需要“无中生有”引入变量的思想和题目中有多个变量需要消元减少变量的思想是否一定要在这个环节中复习到位？还是可以通过一道题目引入变式，不仅渗透这两个思想，而且从多个角度引出与二次函数模型有关的最值问题的几种常用方法？

教学环节二：精讲精练

［例1］如图4，已知∠MON=90°，OT是∠MON的平分线，A是射线OM上的一点，OA=8 cm。动点P从点A出发，以1 cm/s 的速度沿AO水平向左做匀速运动，与此同时，动点Q从点O出发，也以1 cm/s的速度沿ON竖直向上做匀速运动。连接PQ，交OT于点B。经过O、P、Q三点作圆，交OT于点C，连接PC、QC。设运动时间为t(s)，其中0 ＜t＜8。

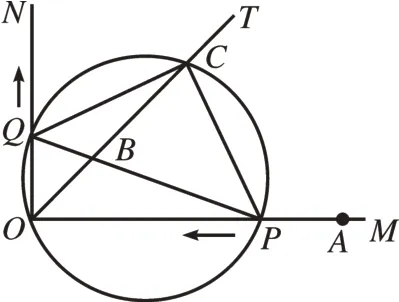
图4

（1）求OP+OQ的值；

（2）是否存在实数t，使得线段OB的长度最大？若存在，求出t的值；若不存在，请说明理由。

设计意图：本题是2020 年苏州市中考题的节选，删去了和本节课主题关系不密切的第（3）小题。本题是一道几何动态型试题，P和Q两点的运动带来了以线段PQ为直径的圆的变化。变化的过程中蕴含着一些不变的量，学生可以从多个角度研究、解决问题。

课堂概况：教师引导学生梳理题目中的条件，形成相关的知识链接，分析后得出解决问题的策略，最终写出解答过程。学生思维活跃，积极探究，先后得出了以下几种解决方案。①看到角平分线的条件，想到角平分线的性质，再过点B分别作OM、ON两边的垂线段，进一步由垂线段想到面积，最后用等积法建立函数关系；②看到45°角想到等腰直角三角形，于是过点B作OM的垂线段，构造一对“A”字相似来建立函数关系；③看到点B是射线OT和线段PQ的交点，且射线OT是直角MON的平分线，想到以O为原点，分别以射线OM和ON所在直线为x轴和y轴建立平面直角坐标系，用求OT和PQ所在直线的交点来解决问题；④把OB放在△OBP中，可以证明△OBP∽△OQC，同时由OQ=TA想到连接CA得△OQC≌△APC，从而通过相似来建立函数关系。

课后思考：整个过程学生思维活跃，参与度很高，能够从多个角度来解决问题，说明以下几个方面都做得不错。①前面的知识内容积累得很充分；②例题选择很恰当；③课堂引导很顺利。不足之处：对于多种不同的解法，教师没有引导学生分析对比，没有尝试思考哪种或者哪几种方法对学生而言比较容易想到。对大部分学生而言，最容易想到的方法往往就是最好的方法。

教学环节三：学情评价

［检测题］已知矩形ABCD中，AB=5 cm，点P为对角线AC上的一点，且AP=cm。如图5，动点M从点A出发，在矩形边上沿着A→B→C的方向匀速运动（不包含点C）。设动点M的运动时间为t(s)，△APM的面积为S（cm2），S与t的函数关系如图6所示。

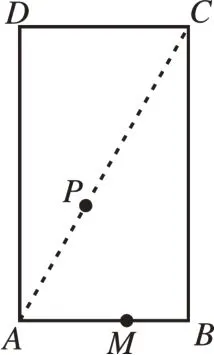
图5

图6

（1）直接写出动点M的运动速度为______cm/s，BC的长度为______cm；

（2）如图7，动点M重新从点A出发，在矩形边上按原来的速度和方向匀速运动，另一个动点N从点D出发，在矩形边上沿着D→C→B的方向匀速运动。设动点N的运动速度为v（cm/s）。已知两动点M，N经过时间x（s）在线段BC上相遇（不包含点C），动点M，N相遇后立即同时停止运动，记此时△APM与△DPN的面积分别为S1（cm2），S2（cm2），①求动点N运动速度v（cm/s）的取值范围；②试探究S1+S2是否存在最大值，若存在，求出S1+S2的最大值并确定运动时间x的值；若不存在，请说明理由。

图7

设计意图：本题是2019 年苏州市中考题。这是一道结合函数图像的几何动态型题目，这一类题目学生往往不是特别擅长。和例1 相比较，这道题在以下两个方面对学生的能力要求更高。①如果没有仔细读题，对“已知两动点M，N经过时间x（s）在线段BC上相遇（不包含点C），动点M，N相遇后立即同时停止运动，记此时△APM与△DPN的面积分别为S1（cm2），S2（cm2）”这段话理解不透，就不会弄清是要研究在两动点M和N相遇后的两个三角形的面积问题，那么问题就很难解决；②如果不能发现S1+S2为定值，而分别去求S1、S2的面积，解答此题会相对麻烦。把这样一道富有挑战性的题目作为检测题，既可以巩固这节课的研究成果，又可以让学生体会到一题多解（求解S1的过程既可以用几何图形的方法，又可以用函数解析式的方法）带来的快乐。

课堂概况：只有5 分钟的练习时间，有些学生一开始就遇到问题，觉得很复杂，原因是他们没有认清两个三角形的面积；有的学生一开始就分别求两个三角形的面积，计算很复杂；也有少数学生想到了比较好的解决方法，但来不及仔细计算。

课后思考：教师除了要给学生留足练习时间，对这一类结合函数图像的几何动态型问题，还要和学生进行深入研究，把这一类问题的共性研究透。另外，教师要进一步培养学生的阅读能力，进而使学生能够更准确、完整地梳理题目中的条件。

三、总结与改进

（一）精心选择例题和练习题

从本质上讲，数学教学就是数学活动的教学。而数学活动又是学生自主建构知识、积累活动经验和发展思维能力的过程。因而，教师必须精心选择教学素材，精心设计教学活动。唯有这样，学生才能更加充分地利用课堂时间探究和分享有价值的数学问题，学会多角度思考问题和解决问题，并在此过程中体会“什么样的方法才是最好的方法”，积累一定的数学活动经验。

（二）强化课堂的开放性

教师要创造更加宽松的学习环境。如果学生的点滴进步被肯定，每一次的思维灵动被赞赏，那么就有利于培养学生的数学学习兴趣，增强学生学习数学的信心，激发学生的探究欲望，由此形成一个良性循环。这对学生形成良好的意志品质、思维品质以及激发学生的创新灵感也十分有利。

当学生探究问题的热情被点燃后，教师要顺势引导他们从不同的角度思考问题，从不同的角度探索解决问题的途径和方法。同时，教师要积极鼓励学生在课堂上分享自己的想法。无论思路和方法如何，教师都应予以肯定，并在此基础上通过师生活动、生生互动，探索出最佳的解题方法。

教师要依据学情适度增设一些开放性问题和变式题让学生探究。学生在探究这类问题的过程中往往会感觉自己是一名探索者，会产生“登高望远”之乐趣，激起进一步学习的兴趣。当然，在探究问题的过程中，教师需要适当引导，鼓励学生大胆猜测、勇于质疑。在解决问题的过程中，教师要引导学生多角度、全方位地思考问题，激活学生的发散性思维和创新思维。

为了更好地打造“探究和分享”数学课堂，教师不仅要积极转变教学观念，不断地学习和研究，还要掌握学科知识体系，把握学生的能力发展目标和认知规律。同时，对于每一项要求学生探究的内容，教师必须先探究，这更有利于教师参与学生的探究活动并给予必要的指导。