砂布页轮表面形貌测量与建模*
2022-03-16吕晓军路丹尼
陈 振,闫 蕊,李 锋,吕晓军,路丹尼,康 超,刘 赞
(1.西安航空学院,西安 710077;2.西北工业大学航空发动机高性能制造工业和信息化部重点实验室,西安 710072;3.江苏科技大学,镇江 212100)
整体叶盘表面质量对航空发动机质量和性能有直接影响。抛光加工作为整体叶盘精密加工的最后一步,其加工表面纹理特征和表面属性主要由磨具表面形貌和加工参数所决定。磨具表面的磨粒切削刃和工件周而复始的相互作用形成了工件表面形貌,磨具表面的磨粒分布情况,如磨粒大小、出刃高度分布、磨粒密度等,直接影响工件材料去除,进而对抛光过程的抛光力、抛光温度、工件表面形貌的形成和磨具的磨损产生重要影响。因此,准确获取磨具表面形貌信息对预测抛光加工表面形貌、磨具磨损等具有重要的作用。
目前磨具表面形貌的测量方法包括触针测量法、复刻法、显微镜法等,在可操作性、测量精度、测量分辨率、数据处理等方面都各有一定的优越性和局限性。Xie 等[1]利用三坐标测量机对#180 粒度的金刚石砂轮进行接触式测量,通过获取的纳米级砂轮表面凸起形貌高度信息,量化分析磨具表面的磨粒出刃高度、磨粒前角和后角等特征参数。由于触针测量法有一定的缺陷,如触针易磨损、测量速度慢等,因此,目前最常用的磨具表面形貌测量方法为非接触式光学测量法。Chen 等[2]利用Zeiss Axio(蔡司)LSM 700 激光扫描共聚焦显微镜(CLSM),通过50 倍光学透镜观测了氧化铝砂轮的3D 形貌,并使用高斯滤波器获得更真实的形貌数据样本。Kapłonek 等[3]利用变焦显微镜对CubitronTMII 和TrizactTM两种磨粒的砂带进行表面测量,通过使用Quanta 200 Mark II 高分辨率扫描电镜获取了3M 237AA 系列4 种粒度的金字塔砂带SEM 显微图像,并对测量区域磨粒的基本几何参数进行表征[4]。
Arunachalam 等[5]在磨具表面形貌建模方面,对棱柱形磨粒涂附抛光盘表面形貌进行激光轮廓仪扫描分析,结果表明,涂附抛光盘中棱柱形磨粒的高度变化主要由磨粒的随机取向而引起。Chakrabarti 等[6]将磨粒形状建模设计为具有120°夹角的方形金字塔,使磨粒高度根据正态分布变化,并且依据磨粒高度重新调整基部直径,将磨粒随机放置在一定半径的砂轮上,最终实现CBN 砂轮表面形貌的仿真。Wang 等[7]对锆刚玉砂带形貌进行观测、分析,结果表明,磨粒突起高度、磨粒间距和磨粒锥角的数学概率分布模型符合高斯分布,而磨粒尖端半径服从Gamma分布。何喆等[8]建立了磨粒随机多面体模型,采用多重叠加随机位移法实现了磨具表面磨料的随机排列,得到了砂带的虚拟形貌。刘月明[9]和Liu[10]等利用球状磨粒在空间的振动模型,并将球体替换为不规则六面体仿真砂轮表面形貌,提出一种计算效率更高的二维切削刃轮廓砂轮模型,并使用3 种不同形状磨粒(球形、截头圆锥形和圆锥形)替代砂轮模型中球形磨粒生成新的砂轮表面形貌。
柱状类柔性磨具结构简单,使用灵活性高且具有一定的柔性,适合对整体叶盘叶片型面进行抛光。砂布页轮是将一定数量的矩形砂布页片呈中心散射状紧密排列,并固结在塑料芯轴上的一类柱状异型涂附磨具。其中心塑料芯轴开有螺纹孔,采用砂布页轮进行抛光加工时,螺纹连杆连接砂布页轮和机床主轴,通过机床主轴带动砂布页轮高速旋转,并利用砂布页片表面的磨粒在工件表面的切削作用实现对工件表面的材料去除[11]。对于砂布页轮柔性磨具而言,抛光过程中砂布页片的卷曲状态随磨具转速和受压缩程度而变化,其表面磨粒参与抛光的状态具有动态变化的特点。
在上述对磨具形貌测量与建模的研究中,主要针对磨具表面形貌进行测量并对形貌参数进行量化评价,再通过粗糙表面仿真技术进行磨具表面形貌的建模。然而,抛光过程中砂布页片的卷曲状态随磨具转速和受压缩程度而变化,其表面磨粒分布状态在抛光过程中具有动态变化的特点,目前鲜有动态磨具形貌模型相关研究。因此,本研究针对砂布页轮柔性磨具,对抛光加工中的砂布页片状态进行分析,并结合粗糙表面仿真技术,建立动态砂布页轮表面形貌模型。
1 磨具表面形貌测量
1.1 测量设置及测量结果
磨具表面形貌测量是在Alicona光学成像公司生产的Infinite Focus G4自动变焦三维表面测量仪上进行[3]。其最大垂直分辨率为10nm,最大水平分辨率为0.44μm,平面扫描范围为540mm×682mm,抗震频率≥35Hz。选取浙江温岭科盈磨具公司生产的P240、P320 两种粒度的黑色碳化硅砂布页轮为研究对象。砂布页轮稳态磨损试验在QMK020 整体叶盘特种抛光机上进行,加工工件材料为TC4钛合金,抛光工艺参数为:主轴转速8000r/min,压缩量0.5mm,进给速度300mm/min。抛光完成后,将表面清理过的采样砂布页片放置于Infinite Focus G4 自动变焦三维表面测量仪10 倍物镜下进行表面形貌扫描。依次扫描4 个区域并拼接,拼接后采样面积为2.85mm×2.16mm。测量结果如图1所示。
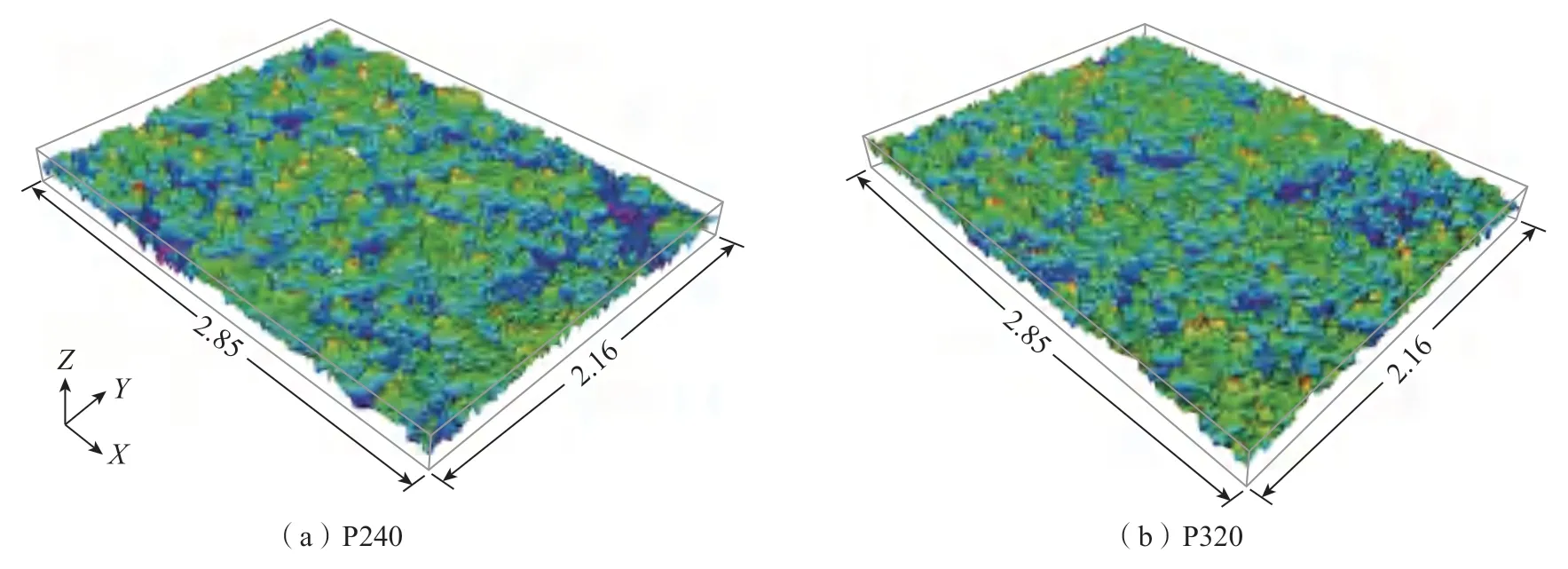
图1 采样砂带页片表面形貌测量结果(mm)Fig.1 Measurement results of sampled belt surface topography (mm)
1.2 测量数据处理
利用Alicona Infinite Focus G4 测量仪配套软件的形貌数据导出功能,将形貌数据存储为一系列的三维点云数据,并利用Matlab 的三维网格绘图功能,导入数据文件后进行数据处理。三维形貌点云数据文件导入Matlab 的显示效果如图2所示。
采用自动变焦三维表面测量仪测得的表面形貌数据含有大量的高频干扰信号,无法直接用于评价磨具表面形貌,为准确反映磨具表面的轮廓特征、磨粒分布以及孔隙特征等信息,本研究采用功率谱密度(Power spectral density,PSD)分析法进行降噪处理[12]。
功率谱密度是原始采样砂布页轮形貌数据进行傅立叶变换模值的平方,其数学表达式为
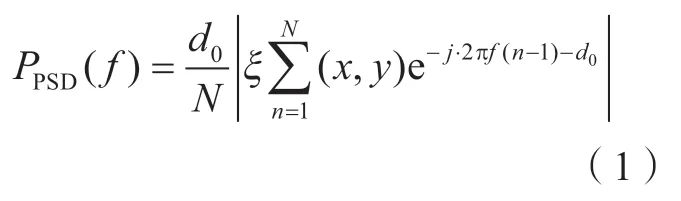
式中,d0为采样长度;N为采样点总数;j为虚数单位;f为信号空间频率;ξ(x,y)为标准化后的幅函数;n为频率离散自变量。
分析可得功率谱密度值整体上随着空间频率的增加呈递减趋势,且在某一临界空间频率fc后持续保持为0 值,可见采样表面形貌的纹理特征主要表现在低频和中频区域。同时,P240、P320 两种粒度砂布页片的临界空间频率fc分别为21.7mm-1、16.2mm-1。对滤波后的数据再进行傅立叶逆变换,可重构磨具表面形貌特征,重构后的形貌特征如图3所示。对比图2,滤波后的磨具表面形貌变化过渡更为自然。

图2 Matlab 显示效果(mm)Fig.2 Matlab display effect (mm)

图3 滤波后的采样砂布页片表面形貌(mm)Fig.3 Surface morphology of sampled belt after filtering (mm)
2 磨具表面磨粒分布特征评价
2.1 磨粒分布密度
在三维形貌的评价中,识别波峰是重要的一步。为了准确识别波峰,本研究根据GB/T 9258.3—2000 涂附磨具用磨料-粒度分析[13]中的粒径数据,P240、P320 两种粒度砂布页片的采样间距取值范围分别为0.0195~0.146mm、0.0154~0.116mm。同时,对磨粒顶点采用八点原则识别磨粒顶点[14],即某点周围8 个点的高度值均小于该点高度,则视其为波峰。识别磨粒顶点如图4所示,可以看出,砂布页片采样区域的磨粒顶点均被识别,无遗漏、无明显的多余。识别磨粒后,可对峰值密度进行统计,即单位面积内的磨粒个数。统计P240、P320 砂布页片的磨粒分布密度分别为35.05/mm2、51.27/mm2。可以看出,磨粒越细则磨粒分布密度越大。

图4 采样砂布页片形貌磨粒识别(mm)Fig.4 Abrasive grain recognition in sampled belt morphology (mm)
2.2 磨粒出刃高度
磨粒出刃高度反映了磨粒的突出高度与磨具表面的位置关系,是十分重要的磨具参数。磨具的磨损速度、抛光后的工件表面粗糙度、残余应力、显微硬度等均与磨粒出刃高度有密切的关系。
磨具表面磨粒出刃高度分布一般为正态分布或非正态分布。高度频率分布直方图通过计算数据频率分布,可直观地体现高度数据是否服从正态分布。P240、P320 采样砂布页片磨粒出刃高度频率分布直方图如图5所示。从高度频率分布直方图可观察到,磨粒出刃高度的概率分布均具有正态分布特征,且磨粒粒度越细,磨粒整体高度越低,磨粒数量越多。
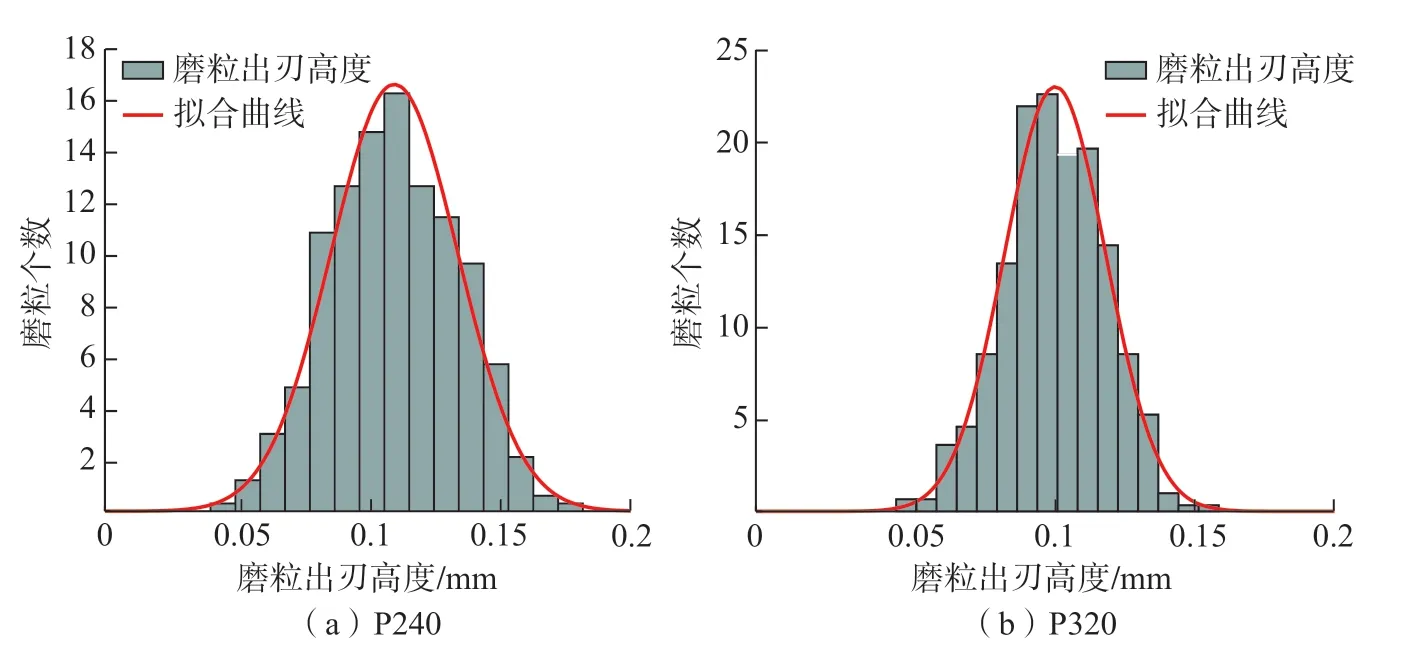
图5 采样砂布页片形貌磨粒出刃高度分布直方图Fig.5 Histogram of height distribution of abrasive grains of sampled belt
3 磨具表面形貌生成算法
3.1 磨具表面三维形貌表征参数
为了对磨具表面形貌进行仿真,首先应对采样区域三维形貌的高度方向分布特征和水平方向纹理特征进行统计分析。其中三维形貌高度方向分布特征参数包括均值μ、标准差σ、偏度Ssk和峰度Sku,而水平方向纹理特征则以自相关函数表达。
(1)偏度Ssk、峰度Sku。
偏度Ssk表征的是轮廓高度概率分布曲线的对称程度。与正态分布相比较,绝对值越大表示其形态的偏斜程度越大。定义上偏度是样本的标准三阶中心矩,其数学表达式为

其中,i、j分别为采样点在x、y方向的第i、j个数值;z(i,j)为采样点高度值;M、N为x、y方向采样数量。
峰度Sku表征的是轮廓高度概率分布曲线变化的尖锐程度。其绝对值越大表示与正态分布相比较,其分布曲线的陡缓程度越大。定义上峰度是样本的标准四阶中心矩,为

对于正态分布表面,分布特征参数中均值为0,偏度值为0,峰度值为3。对P240、P320 两种粒度砂布页片采样区域形貌减去基准面高度值后,三维形貌的高度方向分布特征参数统计如表1所示。从分布特征参数统计结果中(均值接近于0)可以看出磨具表面形貌高度近似呈正态分布。

表1 采样砂布页片表面形貌高度分布特征统计Table 1 Statistics of height distribution characteristics of surface morphology of sampled belt
(2)自相关函数。
磨具表面形貌可视为空间域内的离散信号,自相关函数用于反映形貌不同位置点的空间关系,是偏移的形貌轮廓和原始形貌轮廓之间相似性的定量尺度。对于轮廓变化剧烈的表面形貌,较小的偏移量也会引起较大的轮廓差异,其自相关函数将立即衰减;而对于轮廓变化相对平缓的表面形貌,即使较大的偏移量也不会引起较大的轮廓差异,其自相关函数则不易衰减。三维表面的自协方差函数形式[15]为
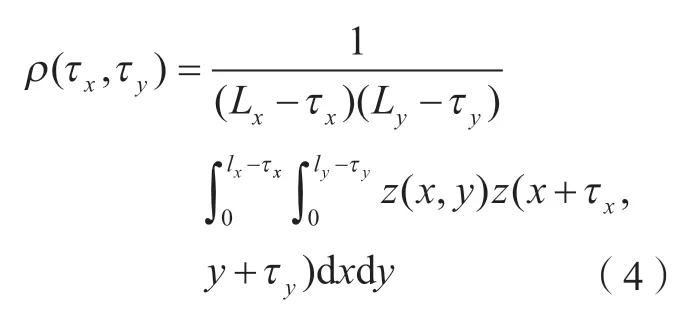
其中,τx、τy分别为x、y方向上的位移差;lx、ly分别为x、y方向的自相关长度。
式(4)的自相关函数为
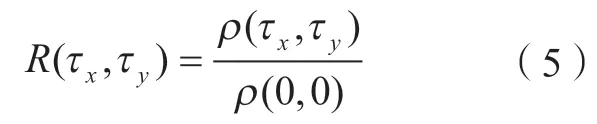
其中,规范化因子ρ(0,0)是表面高度分布的方差。
将自相关函数R进行傅立叶变换可得其功率谱密度函数,即
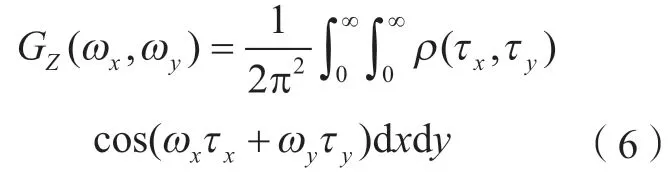
砂布页片表面形貌经过数字采样后成为离散化的随机过程,即z(x,y)取离散化数值,其对应的空间型离散自相关函数形式为
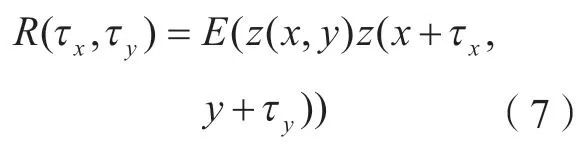
分析得采样砂布页片形貌自相关函数整体呈指数分布。自相关函数图像的指数形式表达式为

式中,σ为均方根粗糙度;lx为x方向自相关长度,ly为y方向自相关长度。自相关长度lx、ly表示形貌轮廓沿着x或y方向衰减到临界值的水平距离。通过空间形貌轮廓在x方向和y方向的自相关长度对比,可判断纹理特征为各向同性还是各向异性。对P240、P320 两种粒度砂布页片采样区域三维形貌的x、y方向相关长度统计如表2所示。
从表2可以看出,砂布页片采样表面纹理在x、y方向上不具有明显的方向性,仅有的微弱纹理方向可以看成是在静电植砂过程中,磨粒排列在传送带上依次进入电场,使得磨粒在传送带运动方向上表现出轻微的方向性。因此,从整体上看砂布页片表面形貌的自相关性质可视为各向同性。

表2 采样页片表面形貌自相关长度Table 2 Autocorrelation length of surface morphology of sampled belt
3.2 磨具表面形貌生成算法
基于AR 模型的二维数字滤波技术[15],可模拟生成具有指定自相关函数的粗糙表面,任意的随机过程η(x,y)通过二维滤波器,即得到随机过程z(x,y),为
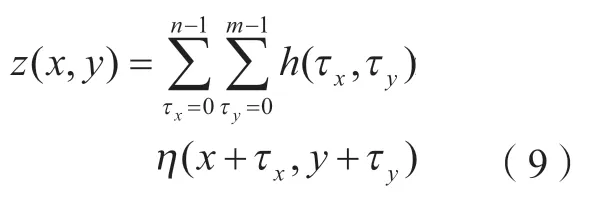
式中,τx=1,2,…,N;τy=1,2,…,M;n=N/2;m=M/2;h(τx,τy)为二维滤波器的冲击响应函数。
式(9)经过傅立叶变换可得函数关系,为
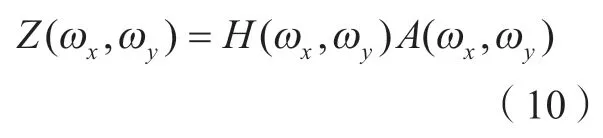
式中,Z(ωx,ωy)为输出序列z(x,y)的傅立叶变换;H(ωx,ωy)为滤波函数h(Δx,Δy)的傅立叶变换;A(ωx,ωy)为输入序列η(x,y)的傅立叶变换,根据传递函数有

式中,C为输入序列的功率谱密度,对于服从正态分布的随机序列,C为常数。
3.3 形貌仿真结果及验证
根据上述表面形貌生成方法,以及采样砂布页片表面三维形貌表征参数,利用Matlab 编写形貌生成程序,得到正态分布的砂布页片表面仿真形貌,如图6所示。

图6 仿真砂布页片形貌磨粒识别Fig.6 Abrasive grain recognition in simulated belt morphology
按前述采样间距统计P240、P320砂布页片仿真形貌的磨粒密度分别为36.03/mm2、51.84/mm2。磨粒出刃高度频率分布直方图如图7所示,可观察到,磨粒出刃高度的概率分布均具有正态分布特征。

图7 仿真砂布页片形貌磨粒出刃高度统计Fig.7 Histogram of height distribution of abrasive grains of simulated belt
仿真表面三维形貌高度分布特征参数统计如表3所示,P240 的仿真页片表面形貌自相关长度x方向和y方向分别为0.187mm 和0.267mm,P320 的仿真页片表面形貌自相关长度x方向和y方向分别为0.182mm和0.239mm。可以看出,仿真得到表面形貌与测量得到的采样砂布页片表面形貌在三维形貌特征上具有相当程度的一致性。

表3 仿真砂布页片表面形貌高度分布特征统计Table 3 Statistics of height distribution characteristics of surface morphology of simulated belt
4 砂布页轮柔性特征
对于砂布页轮柔性磨具而言,抛光过程中砂布页片的卷曲状态随磨具转速和受压缩程度而变化,其表面磨粒参与抛光的状态具有动态变化的特点。因此,在建立砂布页轮表面形貌之前,需要对砂布页轮的柔性特点进行研究,并对抛光加工中的砂布页片状态进行分析。
4.1 砂布页轮运动半径模型
砂布页轮通过一定长度的刀杆与机床主轴相连,工作时随机床主轴做旋转运动,原本相互遮掩的卷曲砂布页片受离心力影响,砂布页片之间的间隙逐渐扩大,卷曲的砂布页片逐渐展开,砂布页轮的运动半径Rn也逐渐增大。在复杂曲面薄壁叶片的抛光过程中,由于砂布页轮具有一定柔性,促使其与叶片表面接触的柔性磨具产生自适应变形,在曲面与磨具之间形成包络面,实现微面切触,从而增加切触宽度,提高抛光效率。
砂布页轮的运动半径Rn随主轴转速n逐渐增大,当主轴转速n超过某一数值,卷曲砂布页片呈近乎直立状态,此时砂布页轮的运动半径Rn几乎不再具有明显的增加趋势。砂布页轮运动半径Rn随主轴转速n的变化趋势,可通过试验获得。对于公称直径12mm(半径r0=6mm)的P240、P320 的碳化硅砂布页轮,通过试验获得的运动半径与主轴转速的关系如图8所示。

图8 砂布页轮运动半径随转速的变化Fig.8 Variation of movement radius of belt flapwheel with spindle speed
对试验数据进行拟合,可得砂布页轮运动半径Rn与主轴转速n的关系为

4.2 砂布页轮柔性模型
不同于砂轮类硬质磨具的磨削加工,柔性磨具在抛光过程中与工件干涉会产生一定程度的柔性变形。涂附磨具的柔性,除了受自身布基材料和涂附胶体的柔性影响之外,主要受其他因素影响。如砂带抛光工艺中,磨具系统的柔性变形主要由接触轮的变形决定,砂带磨具系统的可控范围主要取决于接触轮的尺寸及材料属性;而砂布页轮的柔性是可变的,在工程应用中可以通过控制主轴转速n来影响页轮所受到的离心力,进而实现对磨具的主动柔性控制。
通过砂布页轮的运动半径模型可以观察到,主轴转速n越高,则砂布页轮的运动半径Rn越大。但砂布页轮的柔性可控范围并不随主轴转速n的增加而一直增大。卷曲砂布页片状态随主轴转速的变化如图9所示,主轴转速n较小时,卷曲的砂布页片得不到伸展,砂布页轮运动半径Rn几乎无变化。所以在利用低转速砂布页轮对工件进行抛光时,需要设置较小的压缩量,可以认为低转速下的砂布页轮柔性较小。随着主轴转速n的提高,受离心力的影响,卷曲的砂布页片逐渐得到伸展,砂布页轮运动半径Rn增幅也较大,对工件进行抛光时可调整的压缩量范围也较大,可以认为该转速下的砂布页轮柔性较大。卷曲的砂布页片随着转速的提高而逐渐伸展,并呈直立状态,后续即使主轴转速n继续增大,砂布页轮运动半径Rn的增幅也有限。尽管理论上在高转速状态下砂布页轮运动半径大则可调整的压缩量范围也较大,但由于砂布页片材质限制且砂布页片受到极大的离心力作用,高转速下对其施加较大压缩量易出现飞片现象,所以可认为高转速下的砂布页轮柔性较小。由于较低转速下砂布页轮表面磨粒的切削能力有限,而转速过高的砂布页轮不再具有良好的自适应变形能力,在工程应用中,砂布页轮的转速需控制在一定范围内。
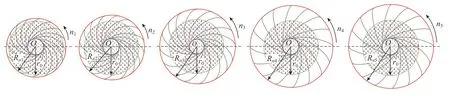
图9 卷曲砂布页片状态随主轴转速的变化(n1<n2<n3<n4<n5)Fig.9 State of curled belt changes with spindle speed (n1<n2<n3<n4<n5)
观察砂布页轮柔性与主轴转速n、运动半径Rn之间的关系,可以看出,柔性较小时,砂布页轮运动半径Rn随主轴转速n的增幅较小;而柔性较大时,砂布页轮运动半径Rn随主轴转速n的增幅较大。为了方便量化砂布页轮的柔性,定义砂布页轮的柔性为运动半径模型的一阶导数。由运动半径式(12)和(13)可得,P240、P320 的柔性模型为
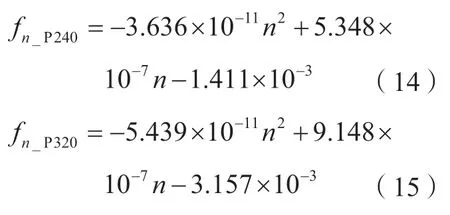
5 砂布页轮表面形貌建模
通过粗糙表面仿真算法可生成与砂布页片测量区域尺寸一致且三维形貌特征一致的表面形貌,但实际应用中的砂布页轮由数十个砂布页片组成且砂布页片间相互遮掩,每个砂布页片仅有末端部分的狭长区域参与抛光过程。因此,后文将重新建立砂布页轮表面形貌。
5.1 静态砂布页轮表面形貌
对于未工作的砂布页轮,可忽略砂布页片之间交接区域的间隙,首先将砂布页轮简化为等直径的砂圈磨具,如图10(a)所示,可根据粗糙表面仿真算法生成与砂圈磨具展开尺寸一致的表面形貌。假设砂布页轮中的所有砂布页片尺寸均相同,且砂布页片为等间距均匀分布,则可根据砂布页片数量和单页片参与抛光的区域尺寸(设此区域宽度为w0),对模拟的砂圈形貌中的非参与抛光区域进行删减,将非参与抛光区域的磨粒出刃高度分布设置为0,即为展开的静态砂布页轮表面形貌,如图10(b)所示。
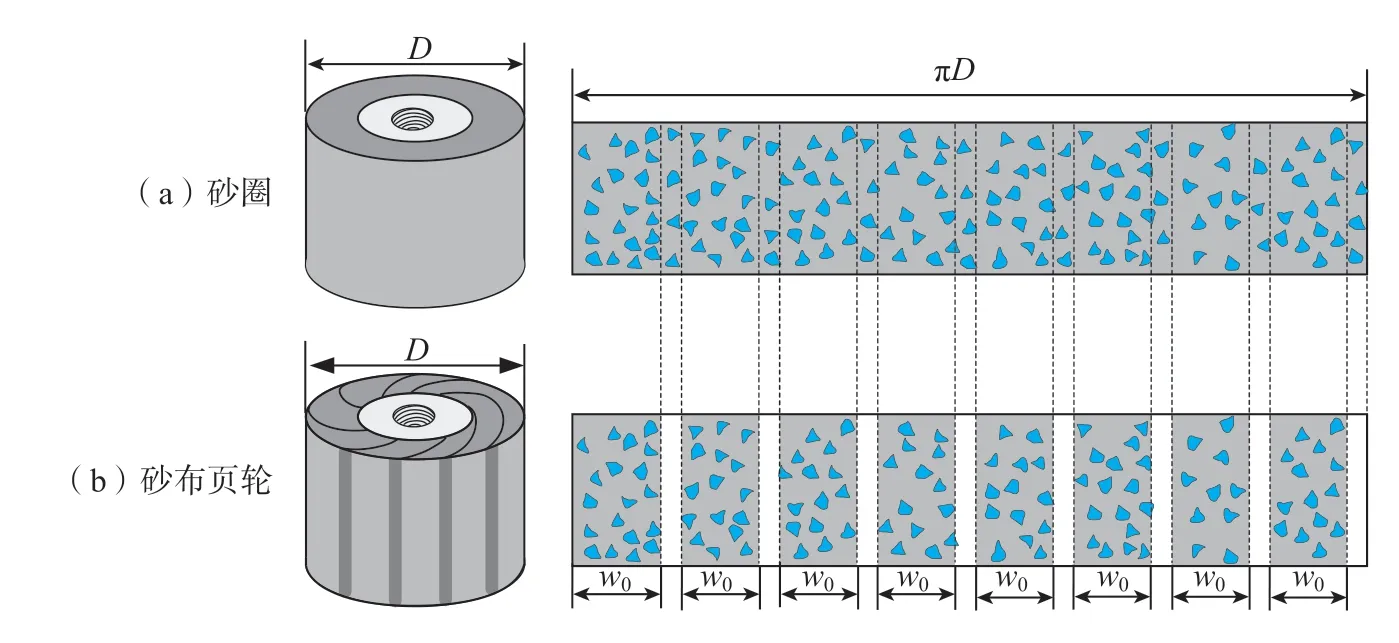
图10 静态砂布页轮表面形貌生成方法Fig.10 Surface morphology generation method of static belt flapwheel
工程中常用的公称直径12mm、宽度12mm 的砂布页轮表面形貌的展开如图11所示。

图11 砂布页轮静态表面形貌模拟结果Fig.11 Simulation results of static surface morphology of belt flapwheel
5.2 动态砂布页轮表面形貌
如图12所示,工作状态下的砂布页轮在主轴转速n时运动半径为Rn;某时刻t,因受到磨具表面磨粒的材料去除作用,工件表面高度由初始位置hw0下降为hwt,砂布页轮在最低点时的运动半径由Rn变为Rt。砂布页轮受到一定程度的挤压,与工件接触时的砂布页片表面磨粒运动轨迹发生变化。由于对工件表面的材料去除起主要作用的磨粒主要为切削最深处的磨粒,因此,可以将t时刻的砂布页轮近似等效为运动半径为Rt的砂布页轮。

图12 砂布页轮等效工作半径Rt 示意图Fig.12 Equivalent working radius of blet flapwheel Rt
抛光过程中砂布页轮与工件的接触,可分为如图13所示1~4 个状态。

图13 砂布页轮与工件的接触状态Fig.13 Contact state of belt flapwheel and workpiece
(1)状态1。旋转砂布页轮的卷曲页片逐渐展开,自工件表面上方垂直向下运动,在未与工件接触时,砂布页轮主轴高度位置haxis与工件初始表面高度hw0的位置关系,有

此状态的砂布页轮表面无磨粒参与抛光过程,则砂布页轮运动半径Rn即为等效运动半径Rt,有

(2)状态2。当旋转的砂布页轮与工件初始接触时,砂布页轮主轴高度位置haxis与工件初始表面高度hw0的位置关系为

此状态即为临界状态,此后砂布页片表面边缘区域的磨粒开始参与抛光过程。
(3)状态3。砂布页轮继续垂直向下运动,随着砂布页轮主轴位置haxis与工件表面的距离逐渐减小,砂布页轮受压缩程度逐渐增大,参与抛光的磨粒运动半径逐渐减小,砂布页轮等效运动半径Rt与运动半径Rn的关系为
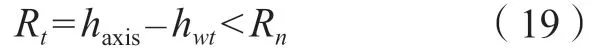
此状态下,随着砂布页轮等效运动半径Rt的减小,表面参与抛光的区域面积逐渐增加,同时工件表面材料被去除。砂布页轮受压缩程度达到极限时,磨粒运动半径与静态砂布页轮半径r0相等,即

受压缩程度达到极限状态时,砂布页片表面参与抛光的区域面积也达到极限,其砂布页片表面形貌等同于静态砂布页轮表面形貌。在工程应用中,一般在机床中设置压缩量ap,与砂布页轮运动半径Rn、静态砂布页轮半径r0的关系为

为避免砂布页轮受压缩程度达到极限状态,加剧磨具磨损以及烧伤工件表面,定义磨粒参与率pt为动态砂布页轮表面参与抛光区域面积与静态砂布页轮表面参与抛光区域面积之比,任意时刻,磨粒参与率pt与砂布页轮等效运动半径Rt成反比,磨粒参与率pt计算方法为
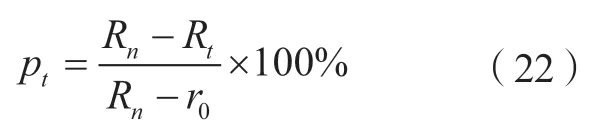
则动态砂布页轮单页片接触区域宽度wt计算方法为

(4)状态4。砂布页轮沿着工件表面以匀速vf直线进给,工件表面材料逐渐被去除,进给一段距离后材料去除深度达到恒定值。设此时工件表面高度为h′wt,则砂布页轮等效运动半径Rt与砂布页轮主轴高度位置haxis、工件表面高度为h′wt的位置关系为

如果进给速度vf足够小,工件表面材料持续被磨粒切除,使得工件表面高度h′wt与工件初始表面高度hw0、压缩量ap的关系为

此时,砂布页轮等效运动半径Rt与运动半径Rn的关系为

结合前述粗糙表面生成算法,砂布页轮表面形貌建模流程如图14所示。
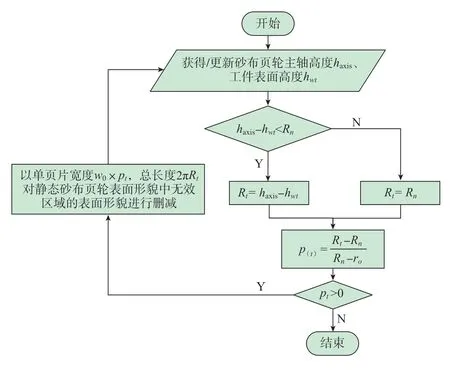
图14 砂布页轮表面形貌的生成过程Fig.14 Formation process of surface morphology of belt flapwheel
综上,可得到各粒度砂布页轮在不同主轴转速n、不同压缩量ap下的等效砂布页轮表面形貌模型,如图15所示。

图15 纱布页轮在不同参数条件下的动态表面形貌(mm)Fig.15 Surface morphology of dynamic belt flapwheel under different parameters (mm)
6 结论
(1)通过自动变焦三维表面测量仪扫描P240、P320 两种粒度采样砂布页片的表面形貌,并通过功率谱密度分析法对形貌扫描数据进行降噪处理,获得可以准确反映磨具表面的轮廓特征、磨粒分布的磨具表面形貌。
(2)通过识别磨粒特征,对磨粒出刃高度进行统计,从高度频率分布直方图可观察到,磨粒出刃高度的概率分布均具有正态分布特征,且磨粒粒度越细,则磨粒整体高度越低,而磨粒数量越多。
(3)基于AR 模型的二维数字滤波技术生成具有指定自相关函数的粗糙表面,并结合砂布页轮磨具柔性特性获得静态和动态砂布页轮表面形貌模型,为砂布页轮抛光过程优化、抛光过程建模,以及砂布页轮光表面形貌形成建立基础。
