基于涡致振动的压电能量收集阵列的仿真与实验

于慧慧，李 莉,2，王永耀，马雄飞，陈 鹏

(1．沈阳化工大学 计算机科学与技术学院，辽宁 沈阳 110142；2.辽宁省化工过程工业智能化技术重点实验室，辽宁 沈阳 110142)

0 引言

近年来，无线传感器等微电子设备已广泛应用于国防、环境监测及灾难预防等领域，依赖传统的化学电池为其供电，对环境有一定污染，频繁更换繁琐，因此亟需解决微电子设备稳定持续供能的问题[1]。涡致振动是自然界中常见的现象，利用涡致振动产生的漩涡作用在压电材料上，使压电材料产生机械振动后将机械能转化为电能，是振动能量收集较常用的方式，现已备受关注[2]。当传感器等设备的供电需求较大时，单一的压电能量收集结构无法满足供电需求，而压电能量收集阵列更易实现能量收集的规模化，为不同供能需求的传感器提供电能。

目前，国内外学者对单圆柱涡激振动问题已有较成熟的研究成果，与单圆柱涡激振动相比，影响多柱体阵列涡激振动的因素较多，主要探索柱体的不同直径比和中心间距比对尾流影响的规律[3-5]。Zrav-kovich等[6-7]将串列圆柱在不同间距下的流动状态分为3类：

1) 当两串列圆柱间距很小时，为近体扰动。

2) 当下游圆柱部分或完全处于上游圆柱的尾流中，为尾流扰动。

3) 当两圆柱间距处于以上两者之间时，流态呈现近体扰动和尾流扰动结合后的状态。

胡彬等[8]基于大涡模拟方法对不等直径的串列双圆柱进行了仿真，分析了雷诺数Re=1 000时不同直径比和间距比情况下流场中涡脱落形态，得到了平均阻力系数、升力系数随直径比(d/D)和间距比(G/D)(d，D分别为下、上游圆柱直径)的变化规律。白旭等[9]在Re=300的条件下探索了d/D和G/D对串列不等直径双圆柱涡激振动特性的影响。研究结果表明，下游小直径圆柱的升力系数和阻力系数均随d/D的增大而增大，两圆柱间的作用力随G/D的增大而减小，当G/D=2，d/D=0.2时，下游圆柱的振幅比(振幅的均方根Yrms与直径的比值)最大可达3.2d。Bernitsas 等[10-12]提出了从流体流动中产生可再生清洁能源的新概念，制作了涡激振动水生能源换能器，首次成功地将海洋能转换为一种可用的能源形式，将其阵列型布置于水中可进行大规模发电。但该结构带有两级传动机制，不适合小型化。Hobbs等[13]设计了一种将圆柱结构通过弹性支撑梁与压电悬臂梁相连接的涡激振动能量收集结构。圆柱因风吹产生的涡激振动现象发生振动，压电材料在弹性支撑梁的带动下产生稳定的振动。将4个相同的俘能结构串列放置进行能量收集。研究结果表明，当fs/fn=1.6 时(fs为旋涡脱落频率，fn为固有频率)，能量收集装置输出功率为96 μW。Shan等[14]分析了串列式压电俘能结构在不同G/D下的输出特性，研究结果表明，与单个压电俘能结构相比，串列式压电俘能结构的输出电压和输出功率较高，有效地输出流速范围得到了显著的改善。

对多柱体阵列的涡激振动研究大多只是流固耦合的实验与仿真探索，对阵列式压电俘能结构的研究较少，但其研究成果中d/D、G/D等参数对两圆柱运动特性的影响为阵列式压电俘能结构的研究提供了参考。因此，本文对压电能量收集阵列进行研究，通过仿真和实验验证了其优越性。

1 数学建模

图1为并联双晶片压电悬臂梁结构示意图。压电悬臂梁的机电耦合可等效为弹簧-质量-阻尼的单自由度系统，圆柱体装配在具有线性刚度和阻尼的弹性基座上[15]。设x方向为来流方向，圆管在y方向自由振动，则弹性支承的单自由度圆管在y方向振动的线性振子方程为

(1)

式中：D为圆管直径；ms为圆管质量；ky为支撑结构的弹性刚度；Ry为压电梁的等效电阻；Cy,v为横向力系数；cy为支撑结构等效阻尼；mf为流体附加质量；Y为方向位移；t为时间；θy为机电耦合常数；ρ为流体密度；U∞为流体速度；Lc为圆柱的长度。

图1 并联双晶片压电悬臂梁结构示意图

涡致振动圆柱尾流的波动特性可用满足范德波尔方程的非线性振子来模拟：

(2)

(3)

式中：ωf= 2πStU∞/D为涡流的脱涡频率，St为斯特劳哈尔数；qy为尾流变量；Ay为尾流振荡器模型的参数；y为尾流振子模型的参数;Cp,y为压电梁的等效电容。

当式(2)右侧为0(指振动频率等于脱涡频率)的情况下时，得到振幅的极限环周期解。静水中的固有频率为

(4)

定义一系列无量纲量为

(5)

(6)

(7)

(8)

τ=ωn,yt

(9)

(10)

(11)

(12)

(13)

(14)

根据式(5)～(14)，则式(1)～(3)可改写为

(15)

(16)

(17)

在俘能结构振动发电过程中，压电悬臂梁自身的损耗与电容值相比极小，可忽略，则电路可等效为一个交流电源与一个等效电容并联，等效电路如图2所示。

图2 等效电路图

电功率为

(18)

对于压电俘能结构上的压电耦合使用无量纲电功率进行计算，可得压电能量收集效率为

(19)

2 仿真及实验设计

2.1 数值仿真设计

利用ANSYS软件对压电能量收集阵列进行流-固-电耦合有限元仿真。压电能量收集阵列的耦合模型图及间距示意图如图3～5所示。图中，L、H分别为纵、横中心距。各阵型的仿真模型原点均位于阻流体的中心处，x轴为流体来流方向，阻流体与入口处的距离均为0.1 m，y轴沿阻流体垂直向上，z轴垂直于x-y面，压电俘能结构主平面均平行于来流方向，放置于阻流体后，阻流体与压电俘能结构均为底端固定，上端自由。为了提高计算精度，阻流体及俘能结构周围的网格划分较密集。

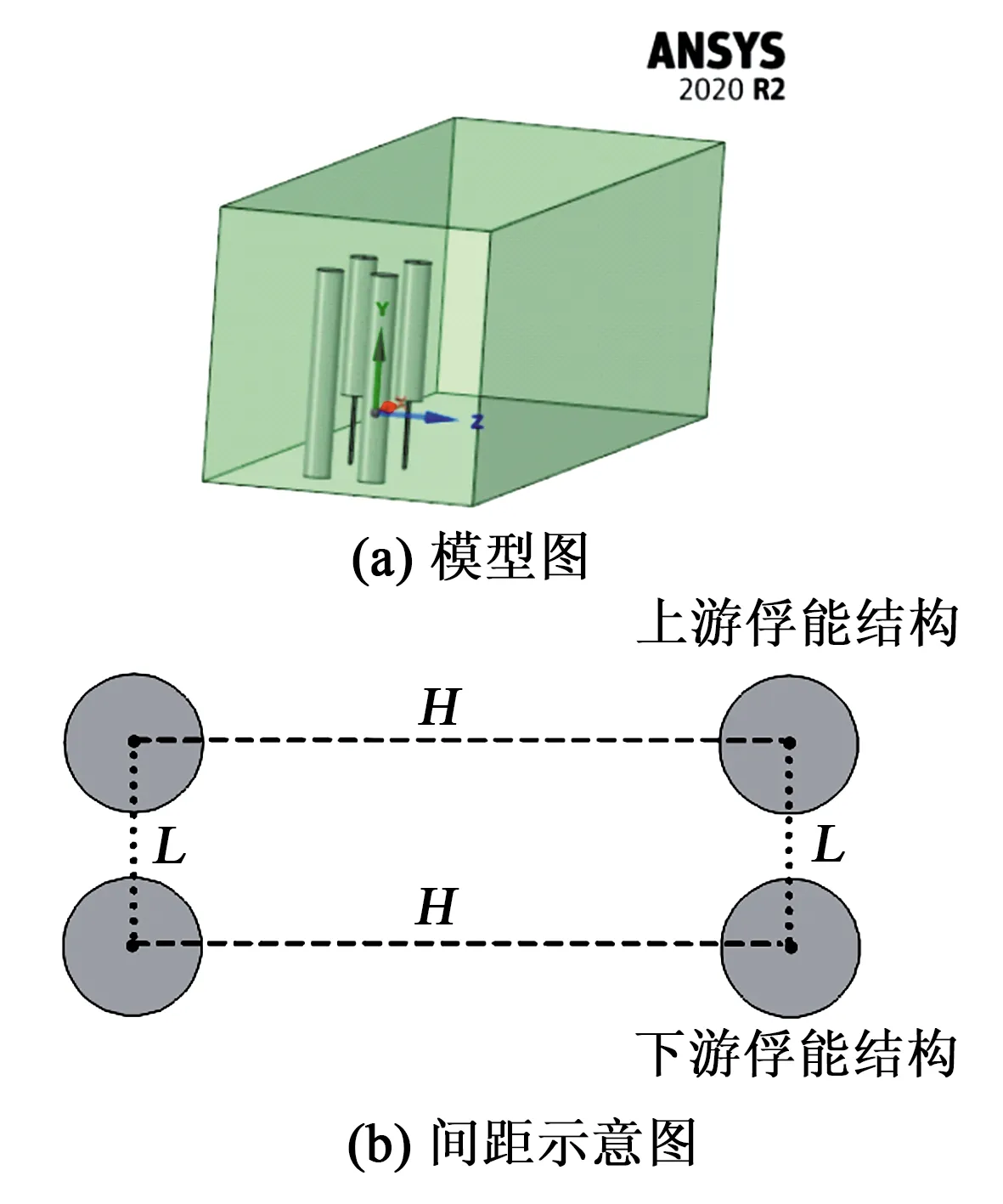
图3 并列模型图

图4 错列耦合模型

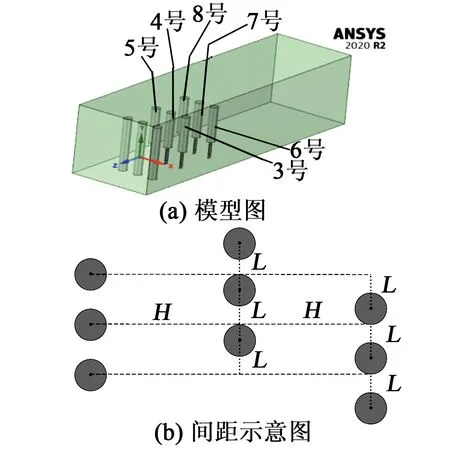
图5 长方阵型耦合模型

2.2 实验系统设计

图6为基于涡致振动的压电能量收集阵列的实验装置图。风洞为直径∅0.315 m的圆筒形，主体管道总长2 m，其圆筒结构可缓冲气流，消除气流涡旋，达到均匀稳定风速的效果，风机选用轴流式风机。实验平台主要包括风洞管道、风速调节器、风速测量仪、虚拟示波器、亚克力板、压电俘能结构及计算机等。实验过程：将固定有圆柱阻流体与压电俘能结构的亚克力板置于风洞管道中，开机后，风机鼓风，将空气吸入，使用风速调节器对风速进行调节，在风洞出口处设置风速仪实时监测风洞中风速的变化情况，数字示波器与计算机连接，实时观测输出电压。并联双晶片压电悬臂梁结构参数如表1所示。

图6实验装置图

表1 并联双晶片压电悬臂梁结构参数

续表

3 结果与分析

3.1 前置阻流体的压电俘能结构的研究

本文首先对前置阻流体的压电俘能结构进行测试。选取风速的测试范围为0～7 m/s，阻流体与阻流圆管均为D=0.02 m的圆柱，阻流体与压电俘能结构间的中心距离不同时，流体流经阻流体后，对后方的压电俘能结构的作用力也不同。为了测试最佳中心距离，两者中心距L分别取3D、4D、5D、6D，得到的振幅响应随风速和中心距的变化如图7所示。

图7 不同中心距的振幅响应随风速的变化

由图7可知，压电结构的振幅响应均随着风速的增加而增加。流速为1～3 m/s时，流速较小，在阻流体后方形成一条较长的低速带区，能量密度较低，此时俘能结构由于流体作用而产生的能量大多用于自身阻尼的消耗，因此产生的振幅较小；流速为3～6 m/s时，随着来流速度的增大，能量密度逐渐增大，俘能结构在阻流体尾部流场的作用下，输入能量远大于自身结构阻尼消耗的能量，此时俘能结构由于流体作用产生的能量大部分表现为振动的形式，振幅较大；在流速为6 m/s时，响应振幅达到最大值后随着流速的增大开始略微减小，说明在流速为6 m/s时达到共振，此时俘能结构处于锁频的稳定振动状态。当L=3D、4D时，阻流体与压电结构的间距较近，流体流经阻流体后，在产生周期脱落的漩涡前便开始绕过压电结构，对压电结构的振幅影响较小；当L=5D时，流体流经阻流体后，产生周期脱落的漩涡，间距适中，脱落的漩涡正好作用在下游的压电结构上，使压电结构产生往复变形，其振幅响应为2.47×10-4m。当L=6D时，阻流体与压电结构距离较远，脱落的漩涡对压电结构作用较小，其振幅响应明显减小。

测试得到最佳中心距L=5D，电压时程曲线如图8所示。由图可知，电压时程曲线呈稳定的正弦函数图像，说明俘能结构受到稳定的力，发生了规律性的往复运动，可收集到稳定的能量。电压随风速的变化折线图如图9所示。俘能结构的输出电压整体上均随着风速的增大呈上升趋势，风速为1.5～3.5 m/s时，电压变化不大；风速为3.5～6.5 m/s时，电压逐渐上升，仿真电压峰值为4.35 V，实验电压峰值为3.08 V，其误差的产生是受仿真过程理想化及实验过程中不可控因素的影响，在可接受范围内。

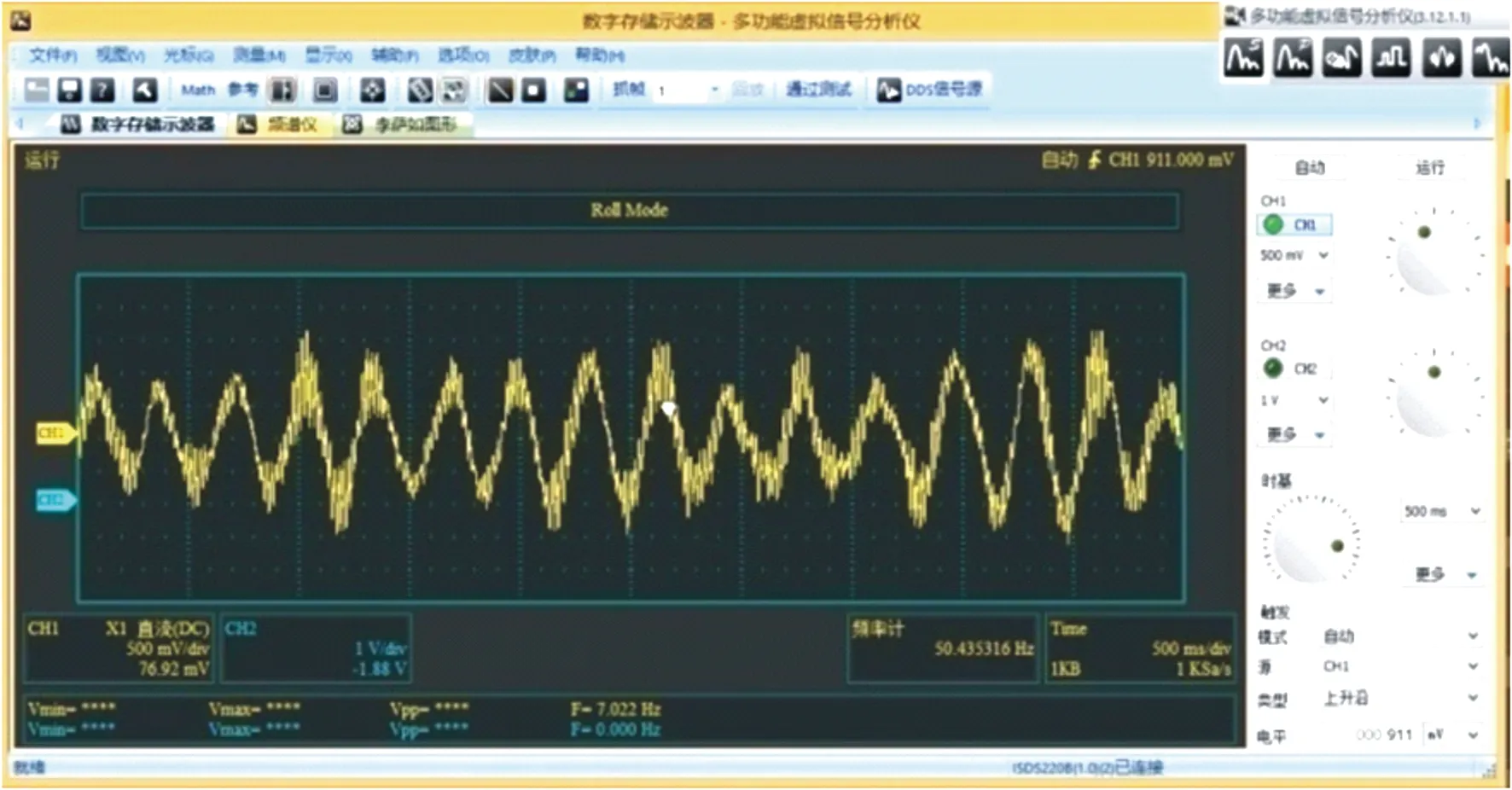
图8 电压时程曲线

3.2 压电俘能结构并列的研究

选取参数完全相同的两个俘能结构(上、下游俘能结构)并列置于流体域中。由前置阻流体的俘能结构研究结果可知，最佳中心距为5D，因此，阻流体与俘能结构之间的横向中心距H=5D保持不变，两个俘能结构间的L/D分别为1.5 m、2 m、2.5 m，风速为0.5～7 m/s，间隔为0.5 m/s，探究两个俘能结构的发电性能。

以来流速度为6.5 m/s，分析流场随L/D的变化情况，如图10所示。两个俘能结构的L/D较小时，两者间流体域的面积较小，阻流体脱落的漩涡边界层基本混在一起，组成一个涡脱落，如图10(a)所示 。随着两个俘能结构的L/D增大，产生双漩涡脱落形态，漩涡之间有交叉，如图10(b)所示。两个俘能结构的L/D较大时，两者之间流体域的面积增大，俘能结构运动状态近似于前置阻流体的单俘能结构，脱落漩涡间无碰撞，如图10(c)所示。

图10 并列俘能结构流场状态图

进一步分析并列双俘能结构的俘能特性，下游俘能结构的输出电压高于上游俘能结构的输出电压，其仿真与实验中输出电压的变化规律如图11所示。在测试范围内，俘能结构的输出电压均随着风速的增大呈先逐步增大后略微下降的趋势，这是由于在风速增大的过程中发生边界层分离的速度逐渐增大，使产生的涡激力和压差较大，形变程度变大，输出电压也随之升高。俘能结构产生的电压均随L/D的增大呈现先增大后减小的趋势，结合流场运动状态，当L/D=2，风速为6.5 m/s时，俘能结构输出电压达到峰值，仿真和实验结果分别为7.39 V、6.09 V。

图11 不同间距下电压随风速的变化图

3.3 压电俘能结构错列的研究

将参数相同的两个俘能结构错列放置于流体域中，阻流体后俘能结构依次称为上游俘能结构和下游俘能结构。阻流体与上游俘能结构的横向中心距及上下游俘能结构之间的横向中心距相等，同为H，同样参考前置阻流体的俘能结构仿真结果，最佳行间距为5D，因此，H=5D。阻流体与上游俘能结构的纵向中心距及上、下游俘能结构之间的纵向中心距相等，同为L，改变L/D，L/D=0.5～2，间隔为0.25。探究错列俘能结构的发电性能。

首先分析两个俘能结构的振动状态，以来流速度为6.5 m/s，L/D=0.5、1、1.5、2为例得到上、下游俘能结构的振动随时间的变化如图12所示。由图可知，上、下游俘能结构均产生了规律的周期性振动，下游俘能结构的振动位移大于上游俘能结构的振动位移，L/D=0.5时，位移较小，上、下游的振动位移分别为4.05×10-5m和5.737×10-5m；随着距离的增大，上、下游俘能结构耦合作用增强，振动位移逐渐增大，L/D=1.5时，形变程度最高，振动位移最大，此时上、下游俘能结构振动位移分别为7.59×10-4m和8.3×10-4m；L/D=2时，振动位移回落，与间距比为0.5时相差不大，上、下游俘能结构振动位移分别为7.7×10-5m和1.16×10-4m。

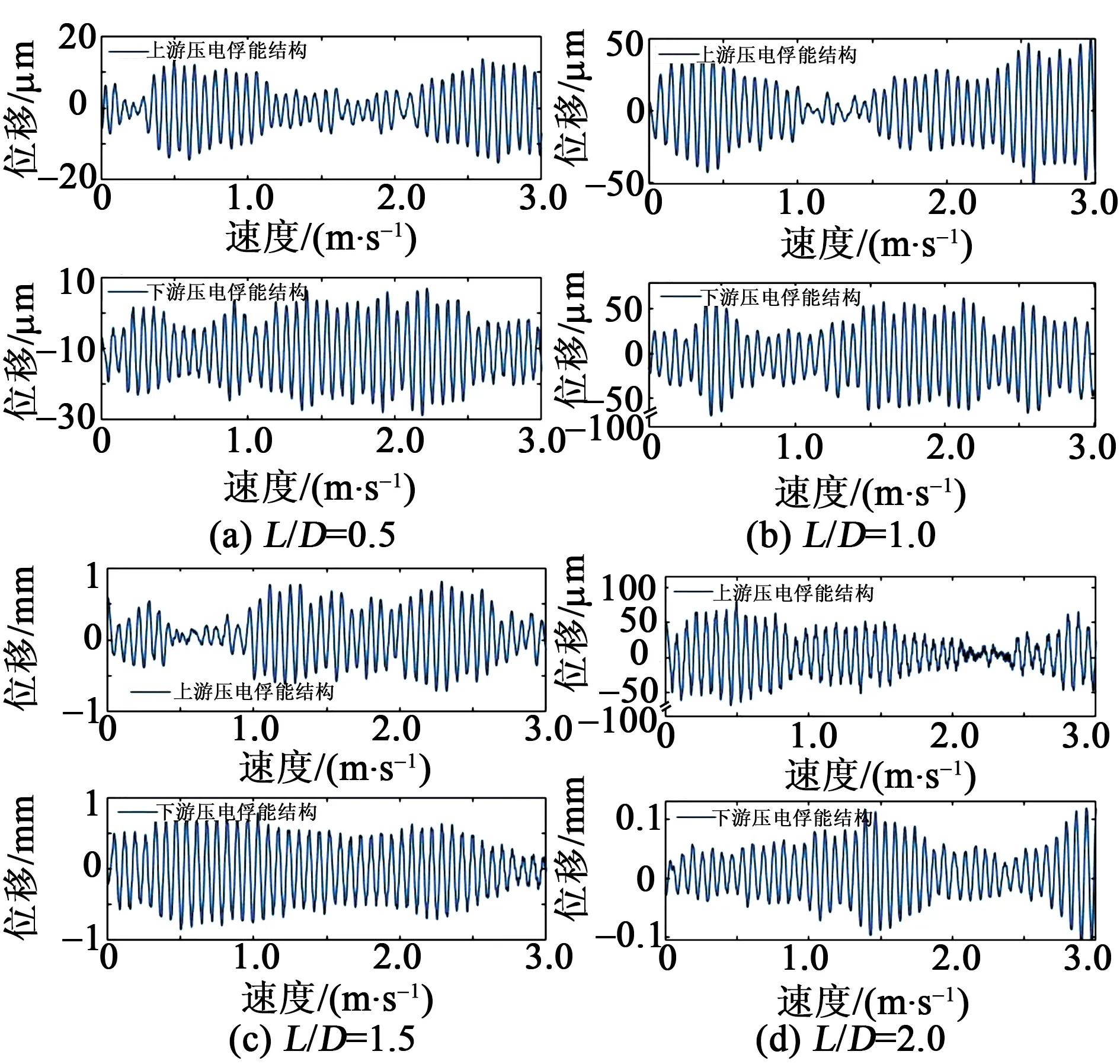
图12 错列俘能结构振动位移曲线图

进一步分析两个俘能结构的振动特性，来流速度为6.5 m/s，以L/D=0.5、1、1.5、2为例，流场的变化情况如图13所示。间距过小或过大时，上、下游俘能结构运动状态类似于单俘能结构，脱落的漩涡不对后方俘能结构产生影响，如图13(a)、(d)所示。当间距适中时，阻流体及上游俘能结构脱落的漩涡作用到后方俘能结构，俘能结构受到自身涡激力及脱落漩涡的作用力，如图13(c)、(d)所示。由图可知，俘能结构的振动位移曲线与流场状态一致。

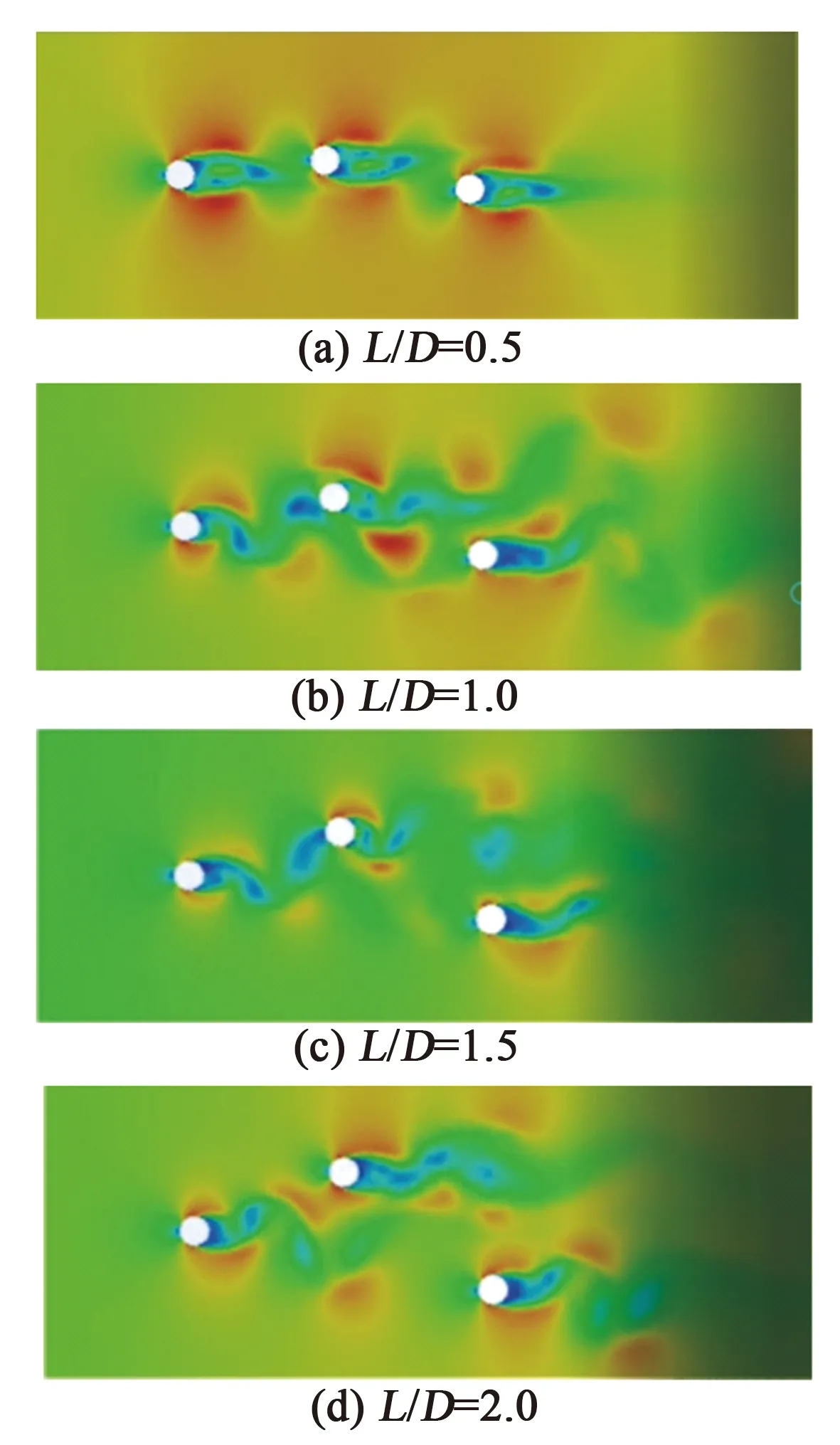
图13 错列俘能结构流场状态图

最后分析了错列阵型上、下游俘能结构输出电压随间距的变化情况，如图14所示。由图可知，上、下游俘能结构的输出电压均随着间距的变化呈先增大后减小的变化趋势，下游俘能结构输出电压大于上游俘能结构。仿真结果中，当L/D=1.5时，输出电压最大，此时上、下游俘能结构的输出电压分别为7.13 V和7.81 V。实验结果中，当L/D=1.25时，上、下游俘能结构的输出电压分别为6.6 V和6.91 V。圆柱直径D=0.02 m，间距比误差仅为0.005 m。

图14 俘能结构错列阵型间距-电压曲线图

3.4 压电俘能结构长方阵型的研究

长方阵型中首行为阻流体，后两行为参数相同的6个俘能结构，为了准确分析每个俘能结构的输出电压，从右到左按3～8号(见图5)的顺序依次对阵型中的每个俘能结构进行编号。仿真过程中阻流体位置不变，相邻行与行之间的H相等且不变，H=5D，即阻流体与俘能结构间的最佳中心距。每行俘能结构间相对位置保持不变，第二、三行俘能结构与阻流体的L向相反方向改变，调整阻流体与俘能结构间的L，使L/D=0、0.5、1、1.5、2、2.5，在风速6.5 m/s下，探究长方阵型下俘能结构的发电性能。

图15为3～8号各个俘能结构输出电压随间距的变化情况。由图可看出，输出电压的变化随间距的增大呈先增大后减小的变化趋势，当L/D=1.5时，各俘能结构的输出电压达到最大，其中6号俘能结构的输出电压大于其他俘能结构，输出电压峰值为10.65 V。俘能结构的长方阵型较特殊，当L/D=0时，长方阵型中包含了串列阵型与并列阵型，此时，阵型中峰值电压为4.8 V；随着间距的增大，长方阵型中出现错列阵型，输出电压均增大，这与仿真中错列阵型的输出电压优于串、并列的规律一致。

图15 俘能结构长方阵型间距-电压曲线图

综上所述，针对压电俘能结构前置阻流体、并列、错列阵型的流体仿真研究发现，由于前置阻流体是单俘能结构，压电俘能结构阵列发电性能较优，其中长方阵型的发电性能最优。发电性能与长方阵型的排列方式有关，长方阵型中既有串、并列阵型的相关特性，又随着间距的改变具有错列阵型的特性，受复杂的尾流作用，表现出更良好的俘能特性。

4 结束语

本文对并联双晶片压电悬臂梁结构进行了数学建模，利用ANSYS仿真软件对压电能量收集阵列进行了数值仿真，并与风洞实验进行了对比，分析了压电俘能结构前置阻流体、并列、错列、长方阵型下的发电性能。研究结果表明，前置阻流体的俘能结构直径为∅0.02 m，在风速为6 m/s，中心距L=5D时，输出电压峰值为4.35 V，验证了结构的可行性。压电能量收集阵列的俘能特性比前置阻流体的单俘能结构优，其输出电压随风速的增大呈整体增大趋势，在最佳风速下，输出电压随间距的增大呈先增大后减小的变化趋势。长方阵型是最优阵型，6号俘能结构在中心距L=1.5D时，输出电压峰值为10.65 V。对比实验和仿真的结果，其变化趋势一致，但仿真环境较理想，实验过程存在不可控因素，导致实验数据在一定程度上小于仿真结果，但基本相符，误差在可接受范围。