弹性振幅放大器对参数激励压电俘能器的影响
2022-03-16秦承武刘景阳孙德华
秦承武,刘景阳,孙德华,杨 磊,谢 进
(西南交通大学 机械工程学院,四川 成都 610031)
0 引言
将环境中振动能量转换为电能的俘能器研究在近20年中已成为研究热点[1-3]。压电式俘能器因具有能量输出密度大,无须启动电源及结构简单等优点而受到广泛关注[4]。
根据外界激励方向的不同,可以将压电式俘能器分为直接激励与参数激励。直接激励的外激励方向垂直于压电梁的梁长方向,而参数激励的外激励方向平行于压电梁的梁长方向。
在直接激励方式下,Zamani等[5]提出了带有弹性振幅放大器的双稳态压电俘能器的二自由度非线性分布参数模型,结果表明,通过调节放大器和俘能器的质量和刚度比可以显著强化外激励,在更宽的频率带宽下提供更高的输出;Galbier等[6]将线性弹性振幅放大器引入非线性俘能器中,数值模拟和实验结果均表明,该组合系统在某些输入频率下能产生更大的输出功率,且有更宽的频率响应带宽。张宇等[7]采用调和平衡法,获得了双稳态压电俘能器与弹性振幅放大器组合系统的位移、输出电压和功率的解析表达式,并讨论了扩大能量俘获频率范围和提高能量俘获效率的机理。
Jia等[8]和Mam等[9]的研究均表明,在外激励的幅值大于激励阈值,当系统发生共振的情况,参数激励压电俘能器的性能优于直接激励压电俘能器。
为了降低参数激励阈值并产生内共振,人们采用了多种增加系统自由度的措施。这些措施在某种程度上也起到了振幅放大器的作用。Yang等[10]提出了一种具有低阈值激励的参数共振俘能器,通过在系统中引入磁力非线性来降低参数共振的激励阈值。研究结果表明,由于垂直梁的参数共振结合了硬化和软化行为,俘能器表现出平坦且较宽的频率响应带宽。Jia等[11]在压电梁底部增加了一个两端固支的水平梁,当水平梁和压电梁的固有频率之比为1∶2时,能够降低激励阈值并增加俘能器工作带宽。Xie等[12]提出了一种T型压电俘能器,当外界激励频率接近俘能器的第一谐振频率时将发生1∶3内部共振现象,此时的能量转换效率和频率响应带宽明显增加。
本文直接将弹性振幅放大器以质量-弹簧-阻尼引入到参数激励压电俘能器中,分析弹性振幅放大器在参数激励压电俘能器中的主要作用,重点研究弹性振幅放大器的刚度系数选取对参数激励压电俘能器的激励阈值及工作带宽的影响,以建立分析弹性振幅放大器各个参数对俘能器性能影响的方法,为弹性振幅放大器的设计提供依据。
1 带弹性振幅放大器的压电俘能器结构及动力学模型建立
1.1 带弹性振幅放大器的压电俘能器的物理结构
带弹性振幅放大器的压电俘能器的物理结构如图1所示。压电梁的梁长方向与振动体的振动方向z(t)一致。压电梁的上末端装有质量为M2的质量块,梁长为La,厚度为ta,宽度为ba。压电片贴在梁的下末端,压电片长度为Lp,宽为bp,厚度为tp。压电梁的下末端通过质量为M1的质量块与弹性振幅放大器连接。

图1 带弹性振幅放大器的压电俘能器结构示意图
弹性振幅放大器主要参数有质量ms、刚度系数ks和阻尼比ξ。
设在外部谐波激励z(t)的作用下,压电梁产生的横向和轴向位移分别为w(x,t)和u(x,t),弹性振幅放大器的输出位移为s(t)。
1.2 带弹性振幅放大器的压电俘能器动力学方程
本文采用扩展哈密顿原理[13]建立系统的动力学方程,扩展哈密顿原理可表示为
(1)
式中:q为压电悬臂梁的广义位移;t为时间;s为弹性振幅放大器的广义位移;V为系统产生的电压;L=T-U为拉格朗日函数,T为系统的总动能,U为系统的总势能;δW为非保守力所做虚功的变分。
T包括梁、M1、M2及ms的动能,则T为
(2)
式中:ma为压电梁单位长度的质量[14];IM2为M2的转动惯量;ψ为压电梁的转角,其转角与梁的横向位移和轴向位移的关系为
sinψ=w′
(3)
cosψ=1+u′
(4)
(5)
假设梁足够细长且不可伸展,根据文献[15],其横向位移和轴向位移的关系为
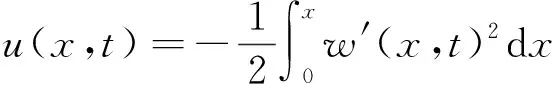
(6)
U包括梁的应变势能和重力势能、质量块的重力势能、弹性振幅放大器的重力势能和弹性势能及压电片的电势能,则有:
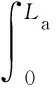
(7)
式中:EI为梁的抗弯刚度,E为梁的杨氏模量;θe为机电耦合系数;Cp为压电电容。其表达式见文献[16]。
非保守力所做虚功的变分为
(8)
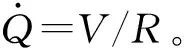
假设梁在振动过程中一阶振型占主导作用,则压电梁的w(x,t)为
w(x,t)=φ(x)q(t)
(9)
式中:φ(x)为梁的一阶振型函数;q(t)为只与时间相关的广义位移函数。
根据文献[12],φ(x)为
(10)
将式(2)、(7)、(8)代入式(1)可得压电俘能器的动力学方程为
(11)
其中:
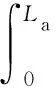
IM2φ′2(La)
(12)
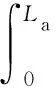
(13)
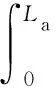
(14)
(15)
(16)
(17)
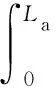
(18)
g1=M1+ms
(19)
g2=ks
(20)
(21)
g4=M1+M2+ms+ma
(22)
g5=(M1+M2+ms+ma)g
(23)
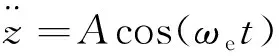
将式(11)无量纲化并转换成状态方程的形式,引入无量纲变换,则有:
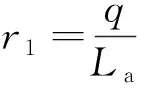
(24)
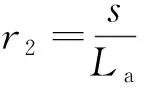
(25)
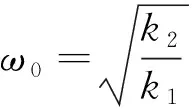
(26)
τ=ω0t
(27)
(28)
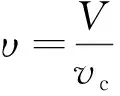
(29)
将式(11)改写成无量纲的动力学方程:
(30)
式中:r1,r2分别为梁和弹性振幅放大器的无量纲位移;β1,β2分别为无量纲的机电耦合系数;υ为无量纲电压;ω=ωe/ω0为无量纲频率;其余参数a,b,c,d,e,f,h,j,c1,λ,ε分别对应无量纲化后的参数k3,k4,k5,k6,g2,g3,g4,g5,C1,Cp,α2。
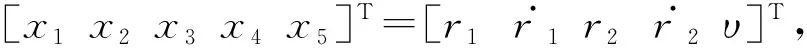
(31)
式中:x1,x2分别为梁的无量纲位移和速度;x3,x4分别为弹性振幅放大器的无量纲位移和速度;x5为无量纲输出电压。
2 带弹性振幅放大器的压电俘能器的特性分析
2.1 压电俘能器系统参数及动力学性能
本文选取的压电俘能器的系统参数及几何尺寸如表1所示。表中,Ep为压电片的杨氏模量,ρa为梁的密度,ρp为压电片密度,d31为压电常数,ε33为介电常数。
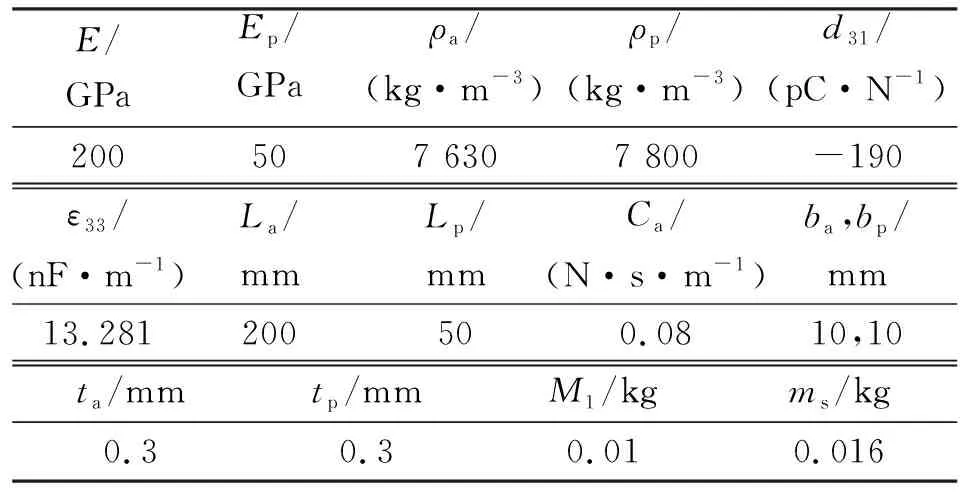
表1 压电俘能器系统参数及几何尺寸
在本文提出的俘能器结构中,M2的大小会影响压电梁的固有频率和系统的平衡点qe。
(32)
当k2>0时,式(32)只有1个解(0,0),即系统只有1个稳定的平衡点(0,0),压电梁未发生屈曲,其固有频率为
(33)
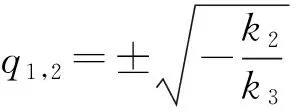
(34)
k2=0是压电梁是否发生屈曲现象的分界点,称此时的末端质量为临界质量(M2c)。由式(13)中k2可得:
(35)
将表1中的参数代入式(35)可以得到M2c=0.062 56 kg。若以M2为变量,则f1及系统平衡点随M2的变化曲线如图2所示。
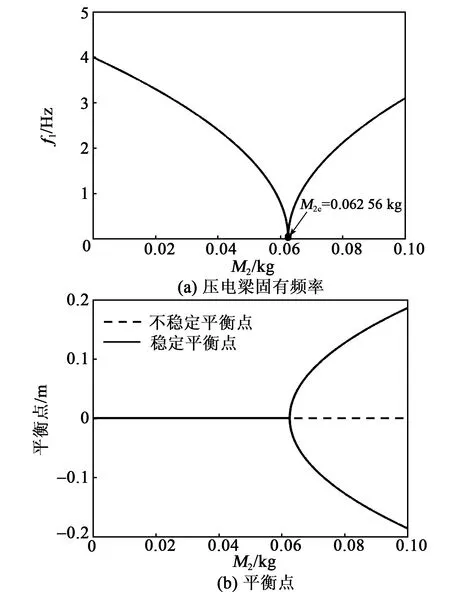
图2 压电梁的固有频率和平衡点
由图2(a)可知,当M2
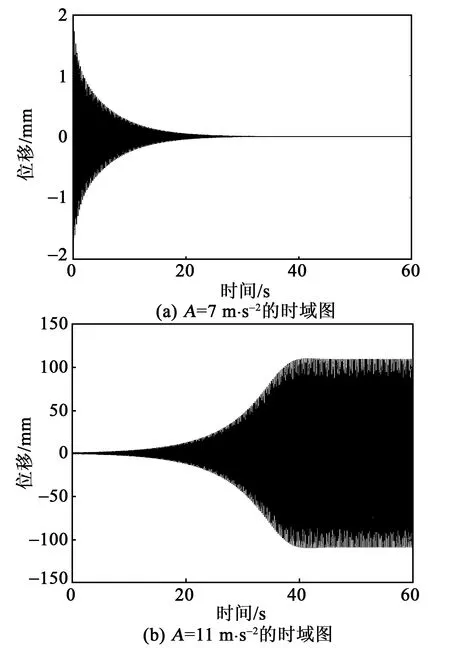
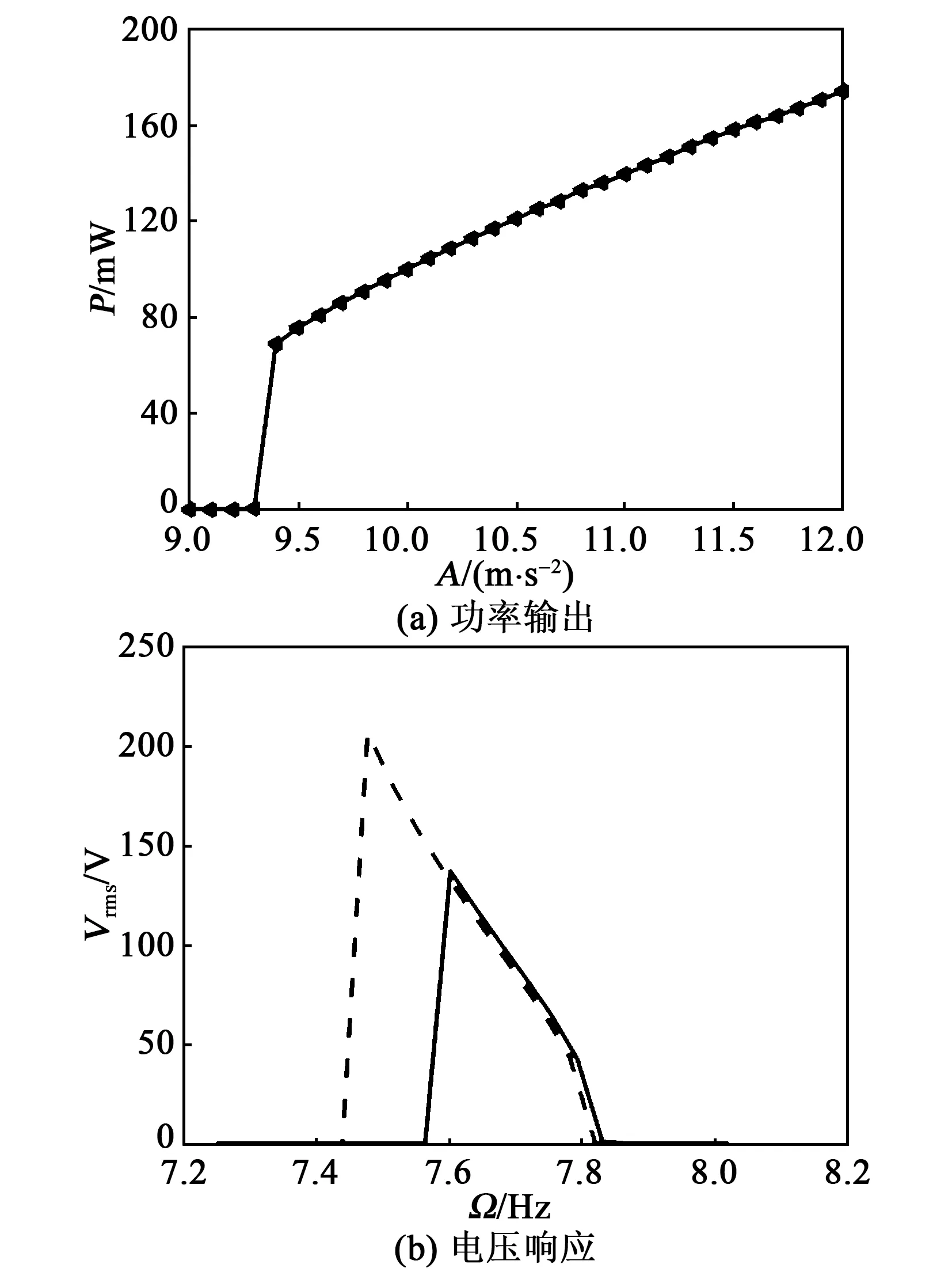
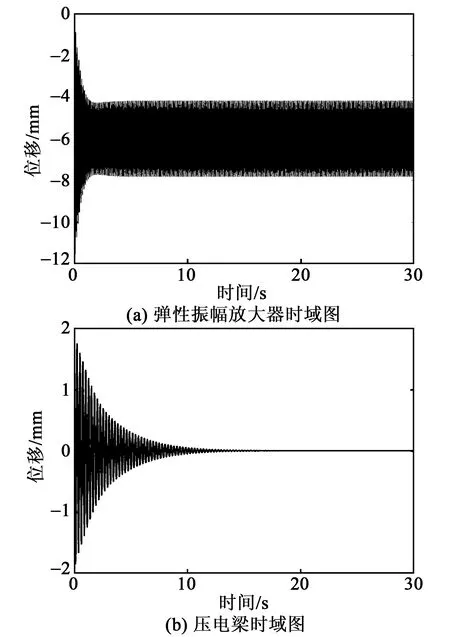
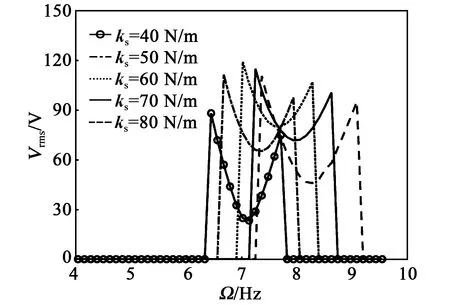
本文主要研究压电梁在未发生屈曲时的动态响应,故在后续的分析中取M2=0.005 kg 为了对比分析弹性振幅放大器在参数激励俘能器中的作用,本节研究无弹性振幅放大器参数共振时俘能器的运动及俘能特性。 将式(11)中涉及到的弹性振幅放大器广义位移s的耦合项舍去,则可以得到无弹性振幅放大器参数激励压电俘能器的动力学方程: (36) 式中qt,Vt分别为未附加弹性振幅放大器时梁的位移响应和输出电压。 本文采用数值仿真法进行分析,为使系统具有一定的初始形变能,取无量纲初始位移值为0.01,其余仿真初始值均取0,R=0.1 MΩ。为使系统产生共振,取Ω为压电梁固有频率的2倍,即Ω=7.64 Hz。在后续的分析中,若未加特别说明,仿真时均取相同的初始值和参数。 图3为无弹性振幅放大器在不同外界激励幅值下的运动特性。由图3(a)可知,当A=7 m·s-2时,压电梁的位移响应最终趋于0,稳定的动态响应输出;由图3(b)可知,当A=11 m·s-2时,压电梁最终具有稳定的动态响应输出。由此可看出,只有当A大于某一特定值时,参数激励俘能器才能有稳定的动态响应输出,将此特定值称为激励阈值。 图3 参数激励无弹性振幅放大器动态响应特性 图4为无弹性振幅放大器参数共振时俘能器俘能特性。 图4 参数激励无弹性振幅放大器的俘能特性 图4(a)是P随着A的变化曲线。由图4(a)可知,当A>9.3 m·s-2时,P从0突然增大,有明显的功率输出,即系统的激励阈值为9.3 m·s-2;随着A继续增大,P与A表现为近似的线性关系。 图4(b)是A=11 m·s-2时,Vrms随Ω的变化曲线。由图4(b)可知,频率响应曲线的左侧出现了明显的突变,表现出软弹簧特性,且压电梁在其固有频率的2倍处,即Ω=7.64 Hz时,发生主参数共振,反向扫频带宽略宽于正向扫频,此时压电梁的频率响应带宽,即俘能器的俘能带宽约为7.82-7.44=0.38(Hz)。 2.3.1 带弹性振幅放大器的压电俘能器发生参数共振时的运动及特性分析 弹性振幅放大器的固有频率为 (37) 当M2 (38) 由第2.1节分析可知f1=3.82 Hz。欲使系统产生参数共振现象,则f2=7.64 Hz。 图5为由式(37)得到的f2随着弹性振幅放大器刚度系数ks的变化曲线。由图5可知,欲使f2=7.64 Hz,则取ks=60 N/m。 图5 f2与ks之间的关系 本文重点研究ks对俘能器性能的影响,分析仿真中取弹性振幅放大器参数ξ=0.1,ms=0.016 kg。 图6为A=0.15 m·s-2时压电梁和弹性振幅放大器的时域图。由图可知,当A=0.15 m·s-2时,弹性振幅放大器的输出位移能够达到稳定,而压电梁的动态响应最终趋于0,说明在A较小时,压电梁不能产生参数共振现象。 图6 A=0.15 m·s-2时压电俘能器的动态响应 图7为A=1.6 m·s-2时压电梁和弹性振幅放大器的时域图。由图7(a)可知,当A=1.6 m·s-2时,在0~4 s,弹性振幅放大器的位移迅速增大;在4~10 s,弹性振幅放大器经过短暂调制后,位移输出迅速减小,10 s后,弹性振幅放大器能够产生稳定的动态响应。从能量的角度来看,前一阶段弹性振幅放大器不断吸收外部能量并产生位移输出,随后弹性振幅放大器将自身能量的一部分转移给压电梁,最终达到稳定运动。由图7(b)可知,在0~4 s,压电梁几乎无位移响应;在4~10 s,由于压电梁吸收了弹性振幅放大器的一部分能量,压电梁的位移迅速增大,随后经过短暂调制,位移输出稍微减小,在这个过程中,相当于弹性振幅放大器“放大”外界激励幅值,促使梁发生参数共振,而在10 s后,压电梁能产生稳定的动态响应。综上所述,激励阈值为0.15~1.6 m·s-2。 图7 A=1.6 m·s-2时压电俘能器的动态响应 图8为带弹性振幅放大器参数共振时的俘能器俘能特性。 由图8(a)可知,系统的激励阈值为0.3 m·s-2,比无弹性振幅放大器的激励阈值(9.3 m·s-2)小,说明引入弹性振幅放大器后,系统的激励阈值会大幅度降低。图8(b)为A=1.6 m·s-2时,带弹性振幅放大器的压电俘能器的Vrms随Ω变化的关系。由图8(b)可知,当A=1.6 m·s-2,即A大于激励阈值时,频率响应曲线左右两侧均出现突变,既有软弹簧特性,也有硬弹簧特性,表现出双跳跃现象[18],正、反向扫频的频率响应略有差异,但梁的电压响应带宽约为8.2-7.05=1.15(Hz),比参数激励单梁俘能器电压响应带宽(0.38 Hz)提高了203%。 图9为A不同时,带弹性振幅放大器的压电俘能器Vrms随Ω变化曲线。由图可知,A越大,Vrms越大,频率响应带宽也越大,并且频率响应曲线向右弯曲的部分更多,表现出更强的硬弹簧特性。当A=8 m·s-2时,频率响应带宽可增加到2.3 Hz。 图9 激励幅值对系统频率响应的影响 2.3.2 刚度系数对带弹性振幅放大器俘能器俘能特性的影响 本文重点研究ks对系统激励阈值和系统俘能特性的影响,对其余两个参数的分析,可仿照本文方法进行。 取ksr=7.64 Hz,图10为ks对系统激励阈值的关系曲线图。由图10可知,带有弹性振幅放大器的激励阈值变化曲线整体呈现下凹趋势,即随着ks的增大,俘能器的激励阈值具有非对称先减小后增大的趋势。取ks=40 N/m,50 N/m,60 N/m,70 N/m,80 N/m时,对应的激励阈值分别为2.8 m·s-2,1.3 m·s-2,0.3 m·s-2,1.0 m·s-2,1.7 m·s-2。ks=60 N/m时激励阈值最小,由第2.3.1节的分析和图5可知,此值恰好为使系统产生内共振的刚度系数,称为共振刚度系数ksr。由图还可知,在ks 图10 刚度系数ks对系统俘能特性的影响 ks对P的影响如图11所示。由图可知,ks=ksr=60 N/m时,激励阈值最小,但是P并不总是最大。当A<3 m/s2,ks=60 N/m时的P始终大于其余ks的P,而当A<3 m/s2,ks=70 N/m时的P比ks=60 N/m时的大。ks=60 N/m,70 N/m和80 N/m时,随着A的增大,P的曲线趋于重合;而ks=40 N/m,50 N/m时,ks越大,则P越大,并且这种规律并不随A的变化而发生变化。总之,在ks>ksr时,ks对P的影响不大,即只有在A较高时,ks对P的影响才不明显;而在ks 图11 ks对系统激励阈值的影响 图12 ks对系统频率响应的影响 由图12可知,随着ks的增加,频率响应曲线整体逐渐向右移动。另外,ks对频率响应带宽及均方根电压峰值均有影响。表2为ks与频率响应带宽之间的对应关系。表3为ks与均方根电压峰值之间的对应关系。 表2 不同ks对应的频率带宽 表3 不同ks对应的均方根电压峰值 从表2、3可看出,频率响应带宽随着ks的增加而增大,均方根电压峰值随着ks的增加而先增大后减少,在ks=60 N/m,即为共振刚度系数ksr时达到最大值。这说明只有f2越接近主参数共振频率,弹性振幅放大器的放大效应越明显,均方根电压峰值越大。但此时频率响应带宽却不是最大的。 本文对弹性振幅放大器在参数激励压电俘能器中的作用进行了仿真分析。研究表明,弹性振幅放大器的加入可使压电梁发生参数共振。当系统发生共振时,系统结合软、硬弹簧特性,不仅能大幅度降低系统发生参数共振的激励阈值,且扩宽了系统的频率响应带宽。 弹性振幅放大器的刚度系数对系统性能的影响较复杂。共振刚度系数ksr可以根据系统产生共振的条件由系统的动力学方程得出。在此刚度系数下,弹性振幅放大器的放大效应较明显。但当刚度系数偏离了ksr时,系统的俘能性能的变化却不同。当刚度系数小于ksr时,平均输出功率、频率响应带宽及均方根电压峰值均随着刚度系数的增大而增大;而当刚度系数大于ksr时,频率响应带宽随着刚度系数的增大而增大,均方根电压峰值随着刚度系数的增大而减小,而平均输出功率会趋于相同。 鉴于弹性振幅放大器的参数对参数激励压电俘能器的影响较复杂,本文后续工作将根据俘能器的应用场景,提出确定各个参数的策略和方法,以使俘能器获得最佳性能。2.2 无弹性振幅放大器参数共振时俘能器运动及俘能特性

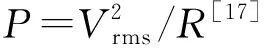
2.3 带弹性振幅放大器参数共振时俘能器运动及俘能特性

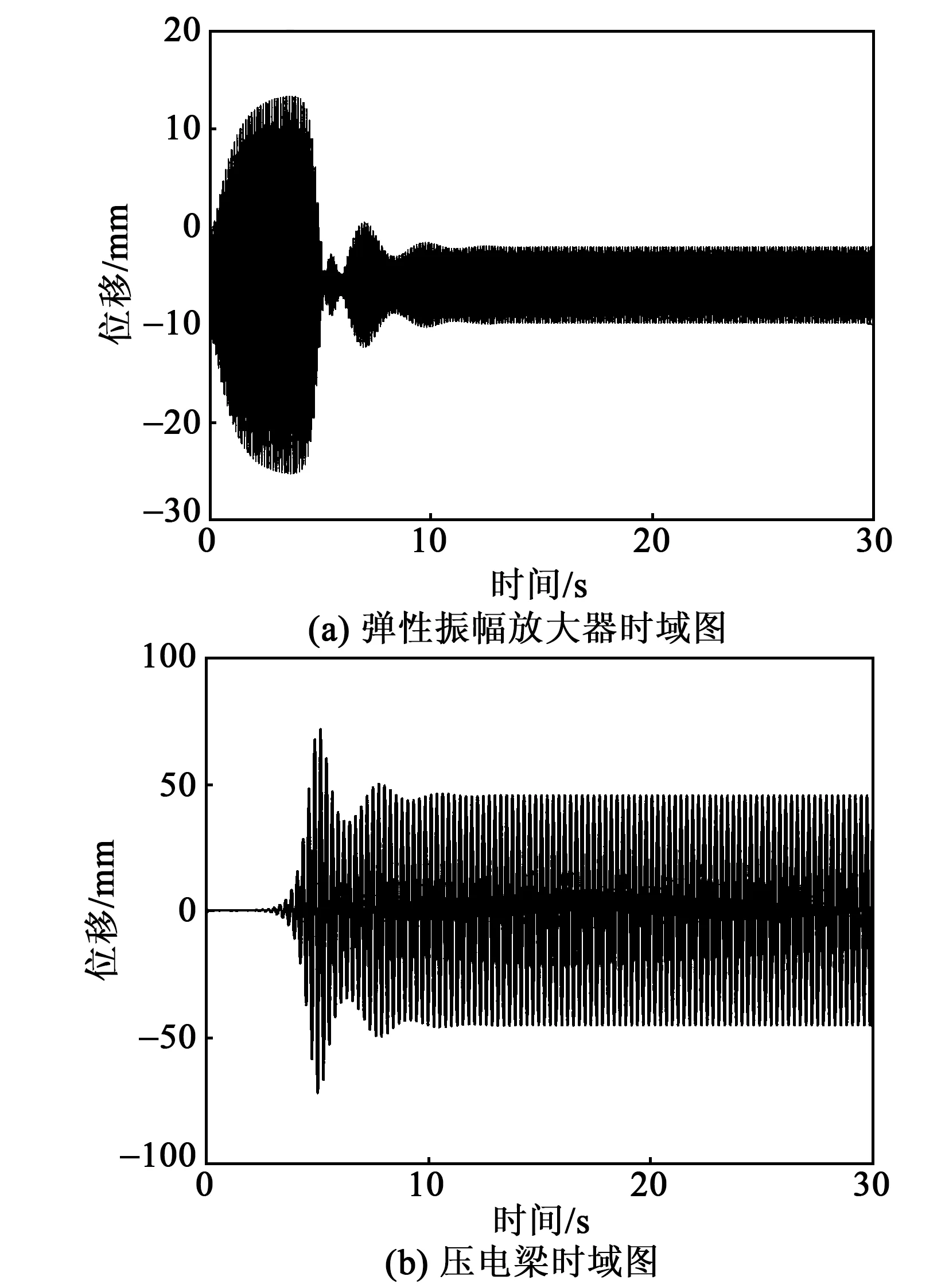
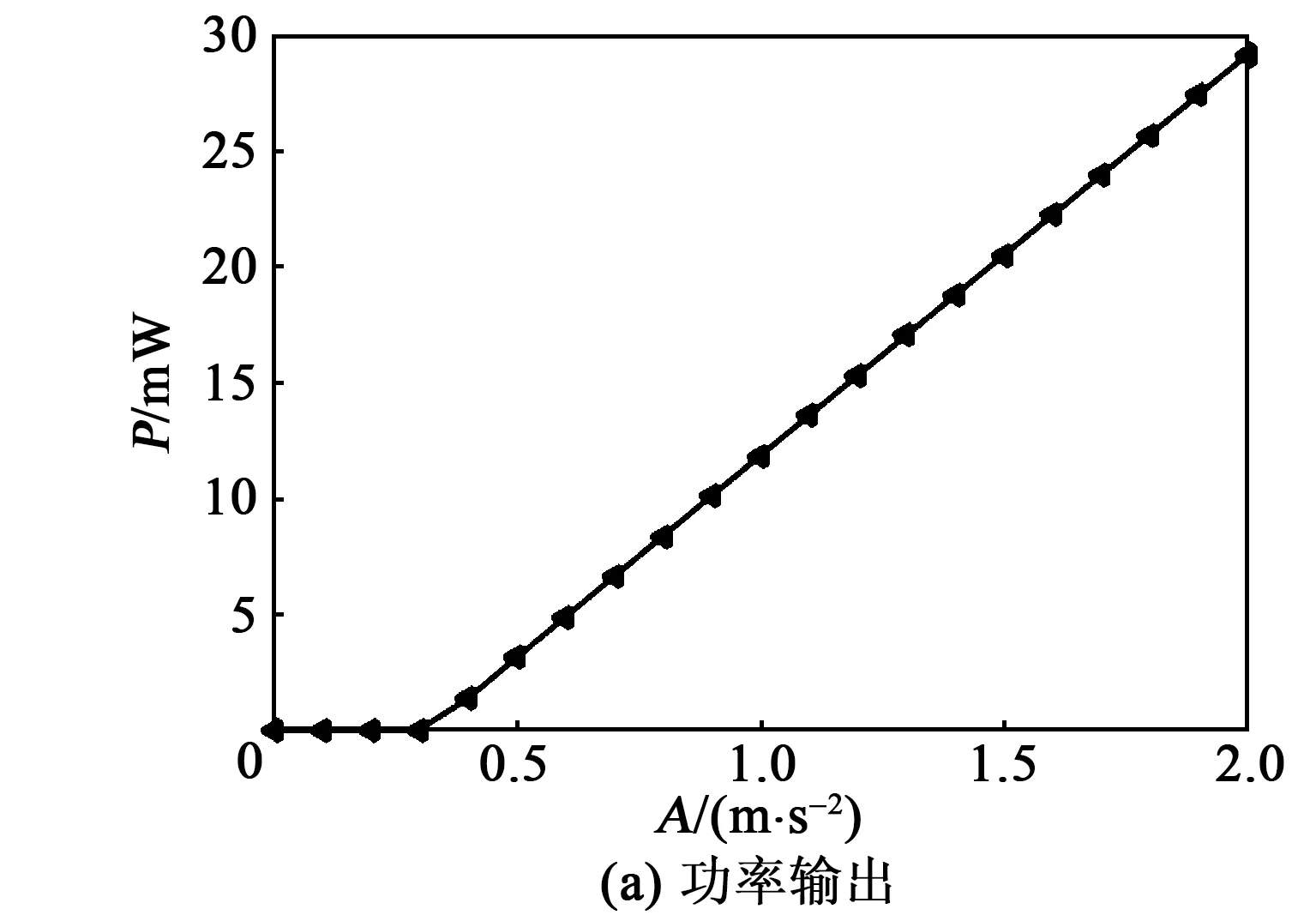

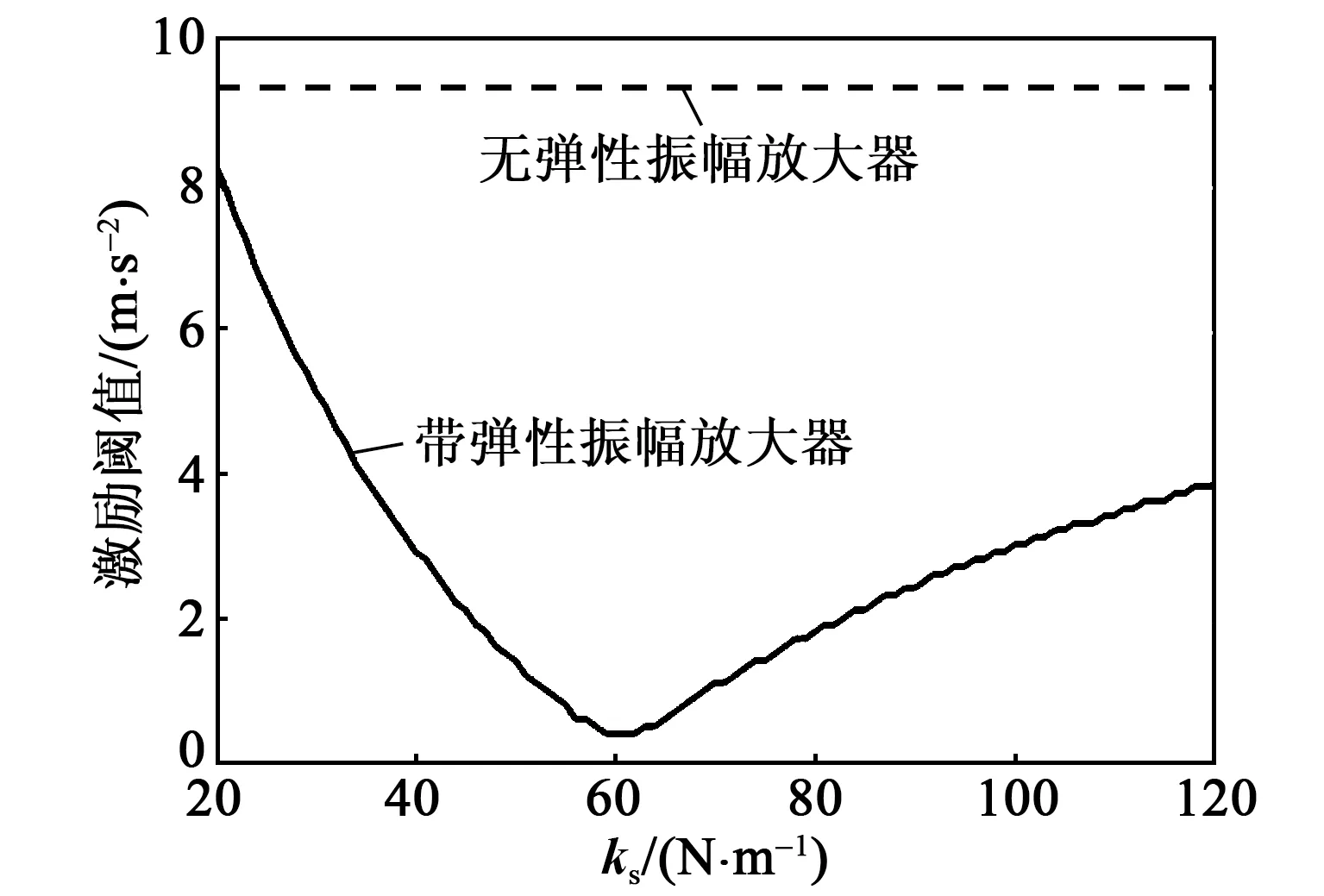
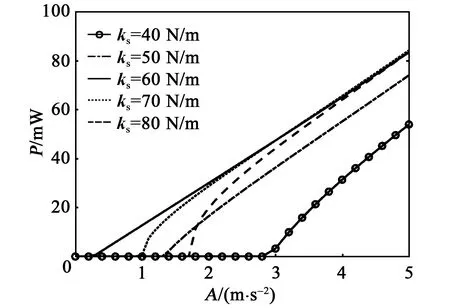


3 结束语
