Kuramoto-Tsuzuki方程一阶线性向后欧拉有限元方法的最优误差估计
2022-03-16崔雪微
崔雪微
Kuramoto-Tsuzuki方程一阶线性向后欧拉有限元方法的最优误差估计
崔雪微
(温州大学数理学院,浙江温州 325035)
对于高维非线性Kuramoto-Tsuzuki方程,给出了一阶向后欧拉有限元全离散格式,并对非线性项采用半隐格式,从理论上证明了离散解的稳定性以及离散解与精确解的无条件最优误差估计.
一阶线性向后欧拉有限元方法;无条件最优化误差估计;Kuramoto-Tsuzuki方程;高维非线性问题
Kuramoto-Tsuzuki方程用于描述分叉点附近的两个系统的行为[1-2],它也可以看作是复杂的Ginzburg-Landua方程的一个特例,该方程被广泛用于描述从非线性波到二阶相变,从超导和玻色-爱因斯坦凝聚到场论中的液晶和弦的大量现象①Feb. 2022 Kuramoto Y. Chemical Oscillations, Waves, and Turbulence [M]. Berlin: Springer Verlag, 1984.等.
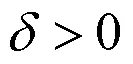
本文主要考虑如下的高维Kuramoto-Tsuzuki方程:
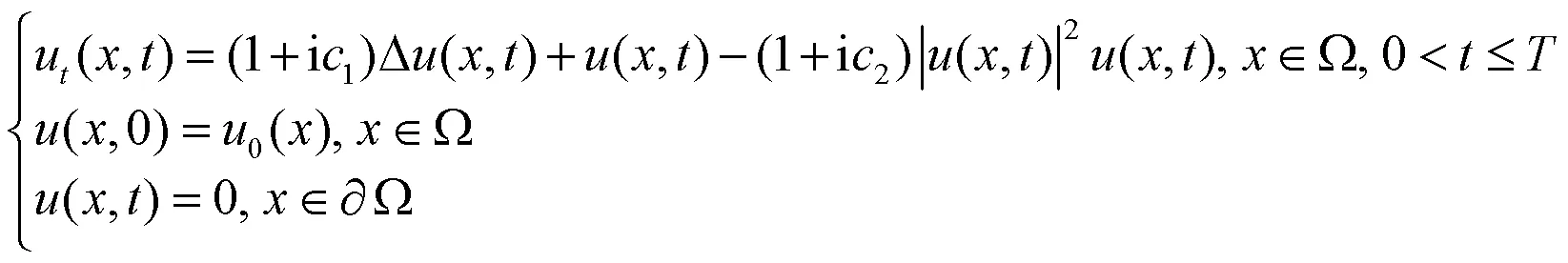
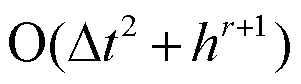
本文建立Kuramoto-Tsuzuki方程的一阶向后欧拉有限元全离散格式,以此证明离散解与精确解的无条件最优误差估计.
1 预备知识
由经典有限元理论可知有:
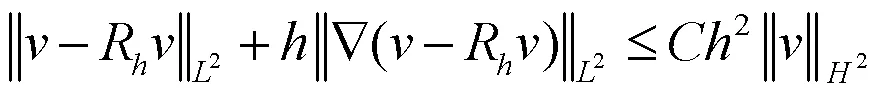
和
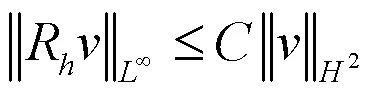
成立.
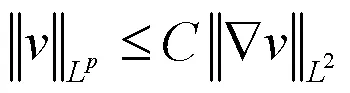
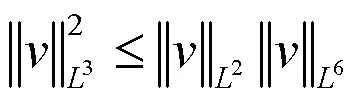
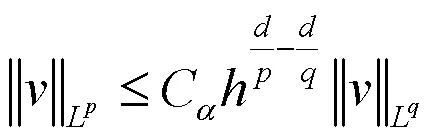
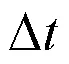
2 主要结果

对于一阶线性向后欧拉有限元解,有如下的稳定性结论.
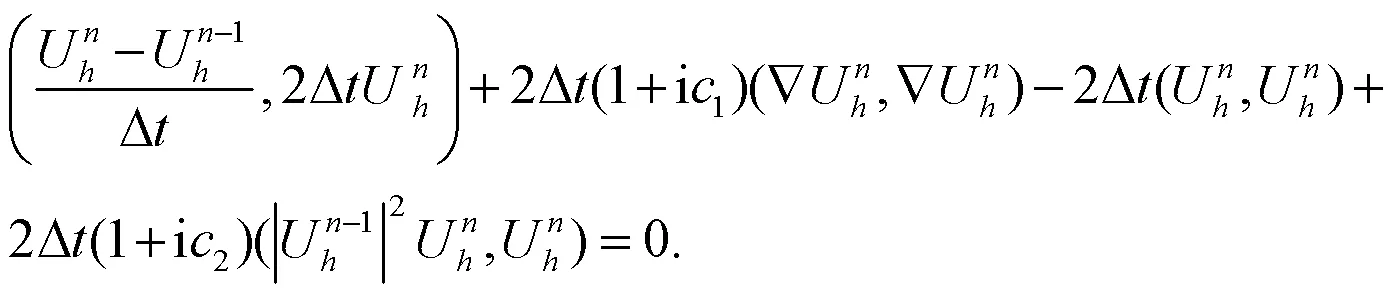
考虑方程(8)的实部,有:
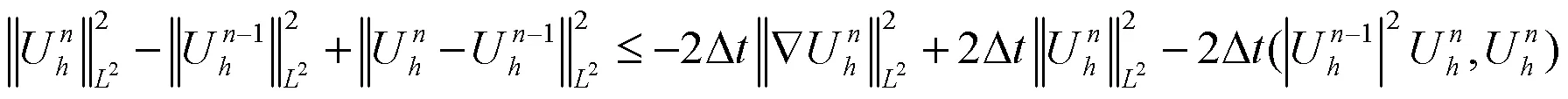
即有:
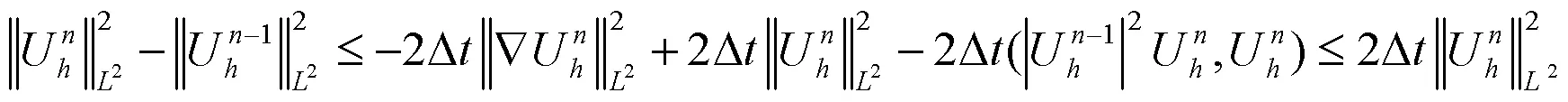
因此有:
引理2得证.
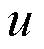
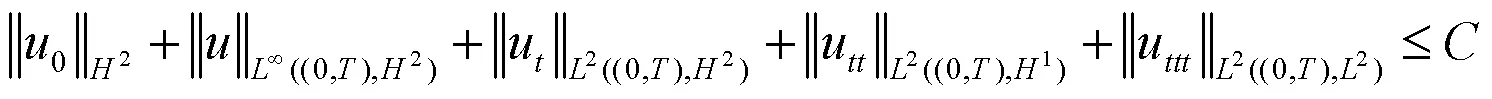
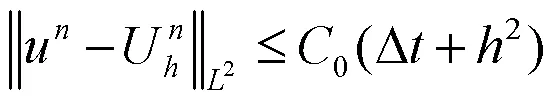
3 主要结果的证明
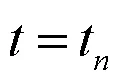
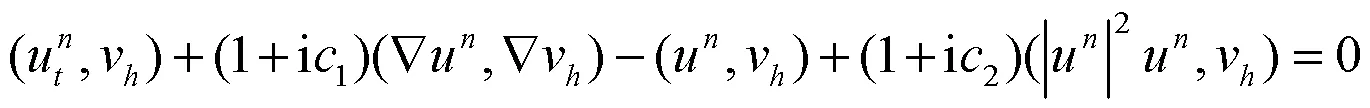

用(11)式减去(7)式,并应用Ritz投影定义,可得:
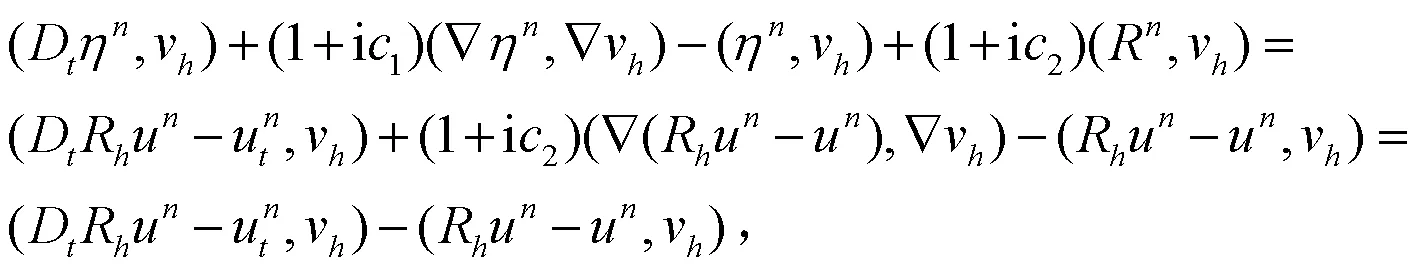
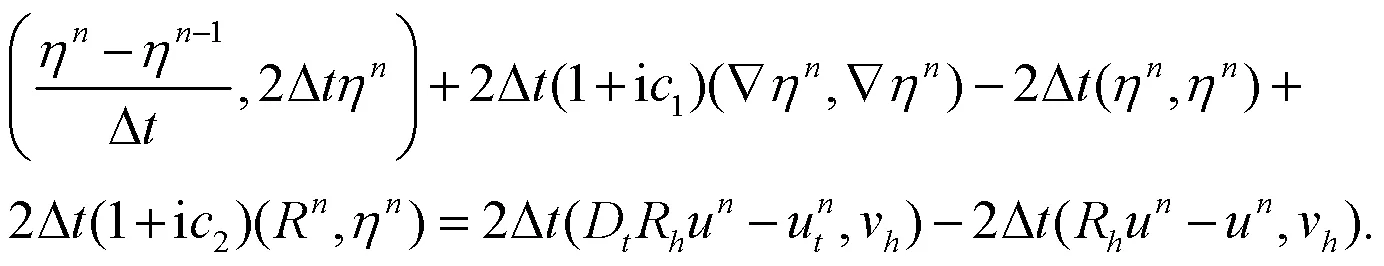
考虑方程(13)的实部,并应用Cauchy-Schwarz不等式可得:
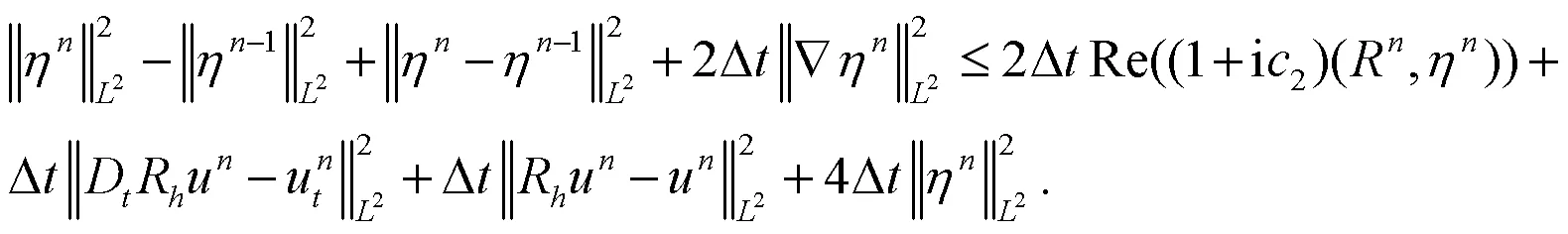
由(2)式及Taylor展式可得:
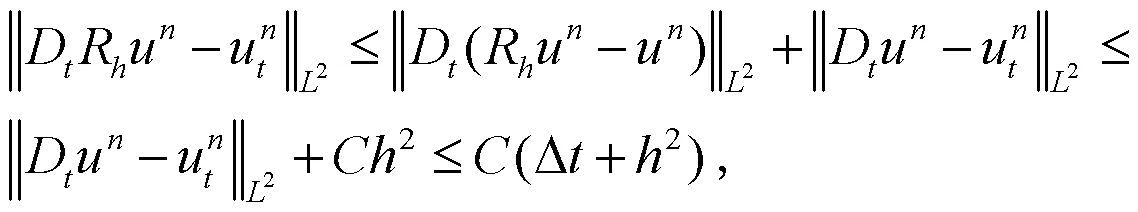
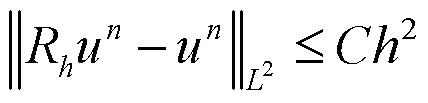
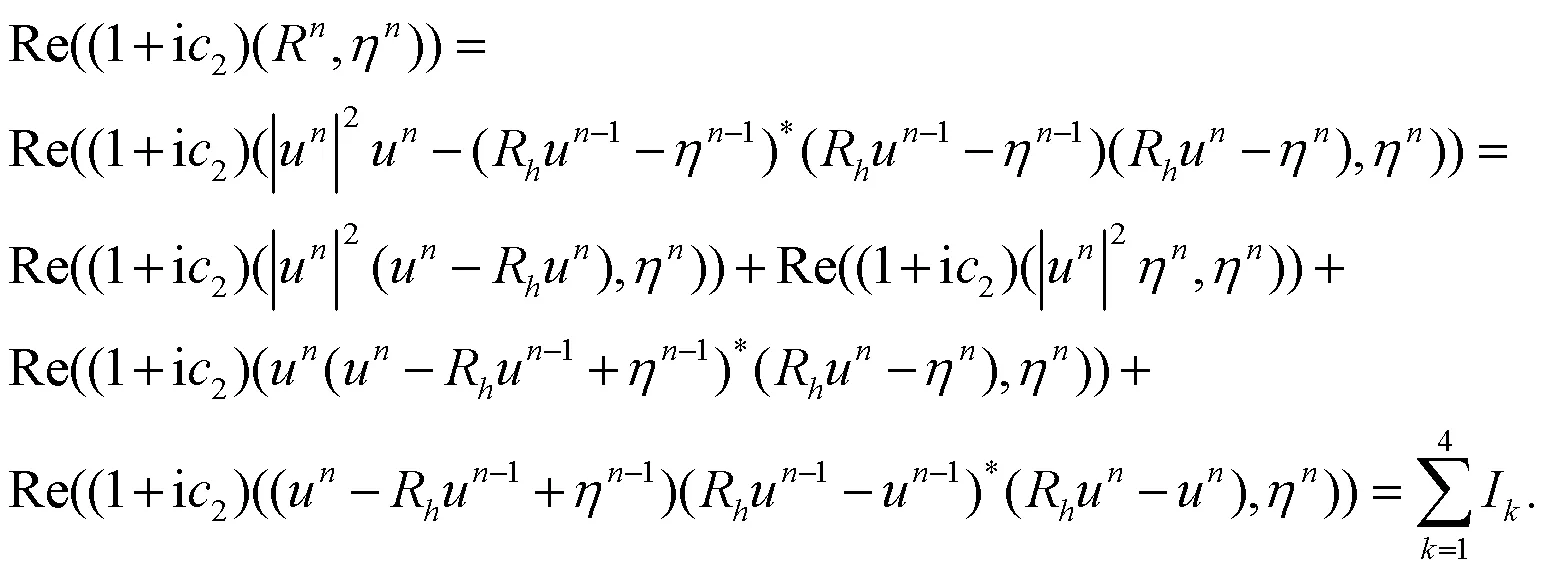
由Young不等式及(2)式可得:
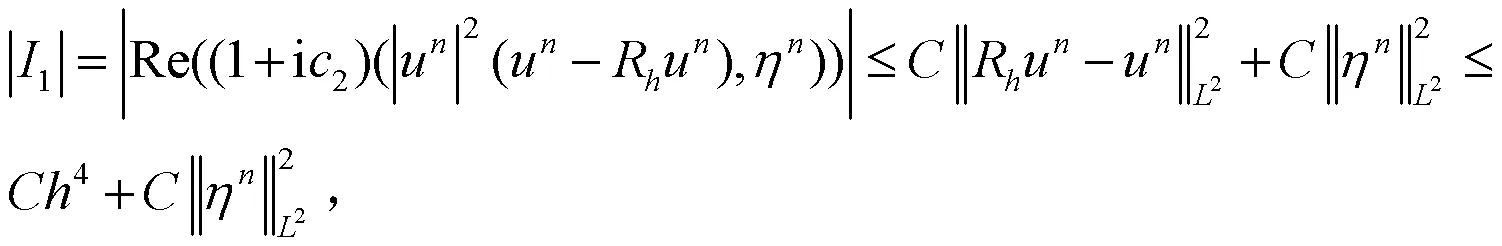

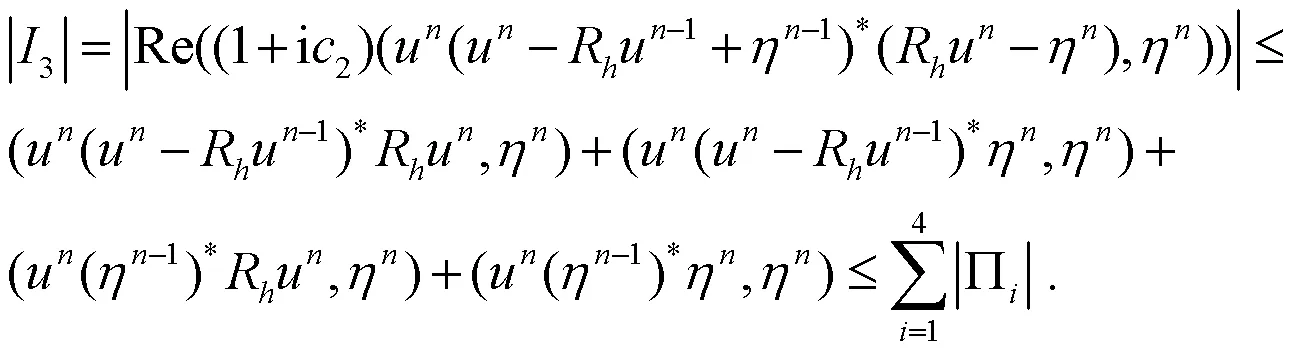
由逆不等式及Young不等式可得:
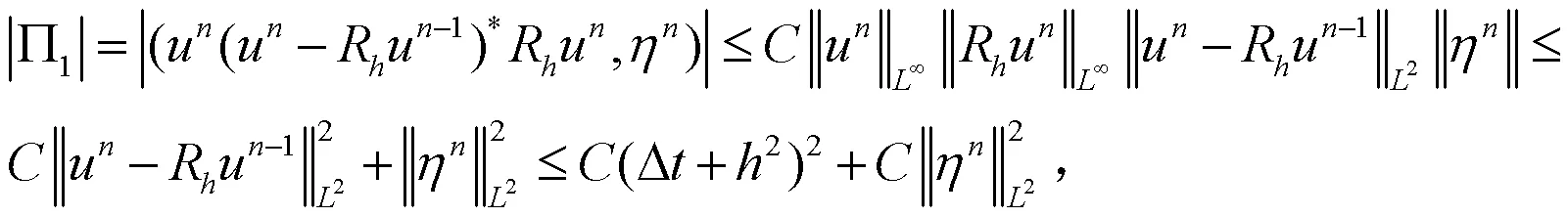
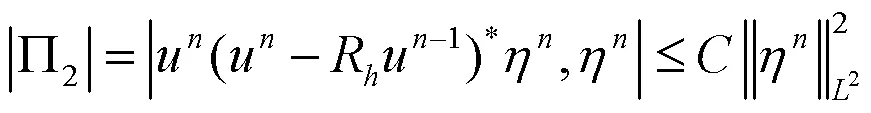
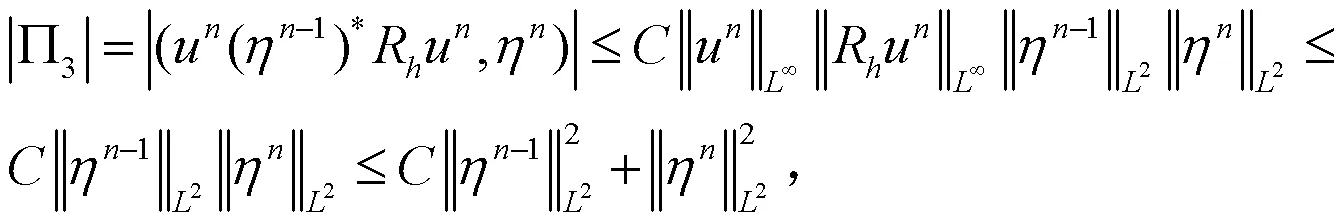
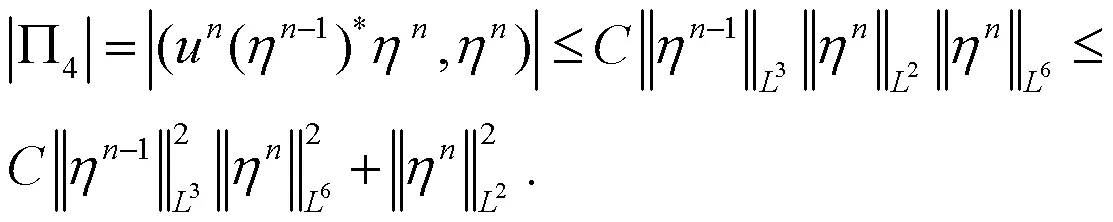
把(21)―(24)式代入(20)式,可得:
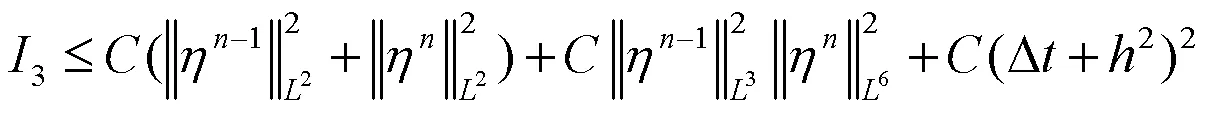
同理可得:
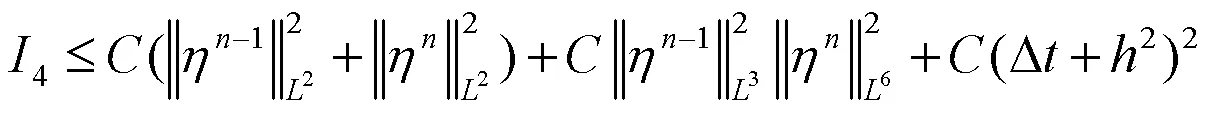
把(18)式、(19)式、(25)式和(26)式代入(17)式中可得:
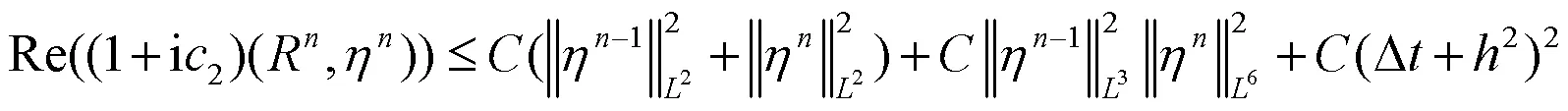
把(15)式、(16)式和(27)式代入(11)式中,可得:
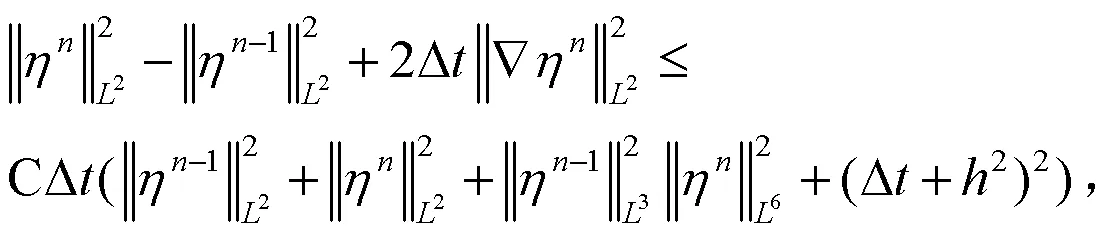
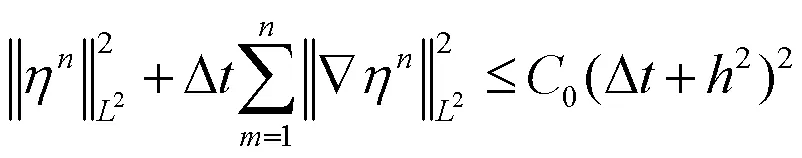
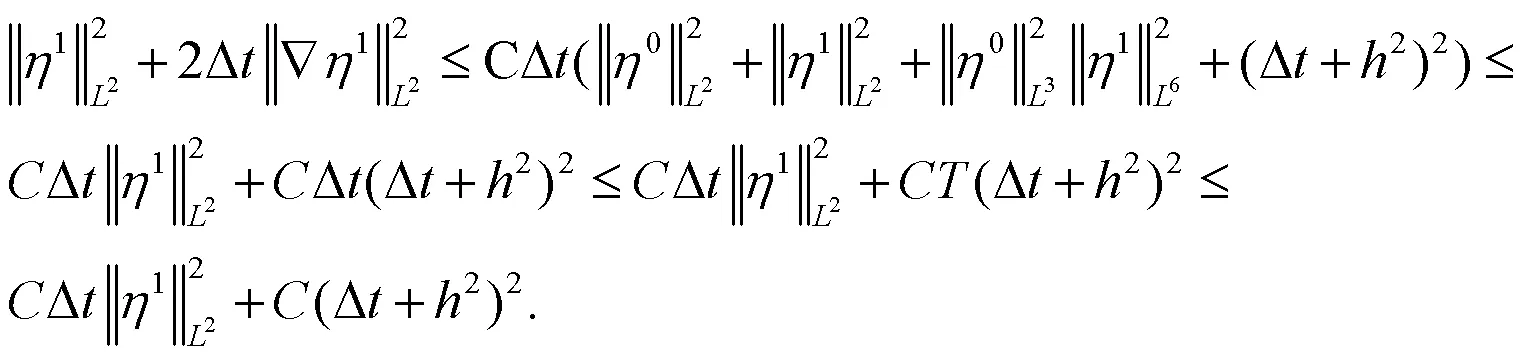
由逆不等式(6)和Sobolev嵌入定理(4)可得:

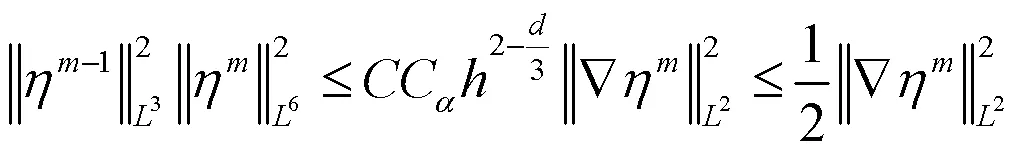
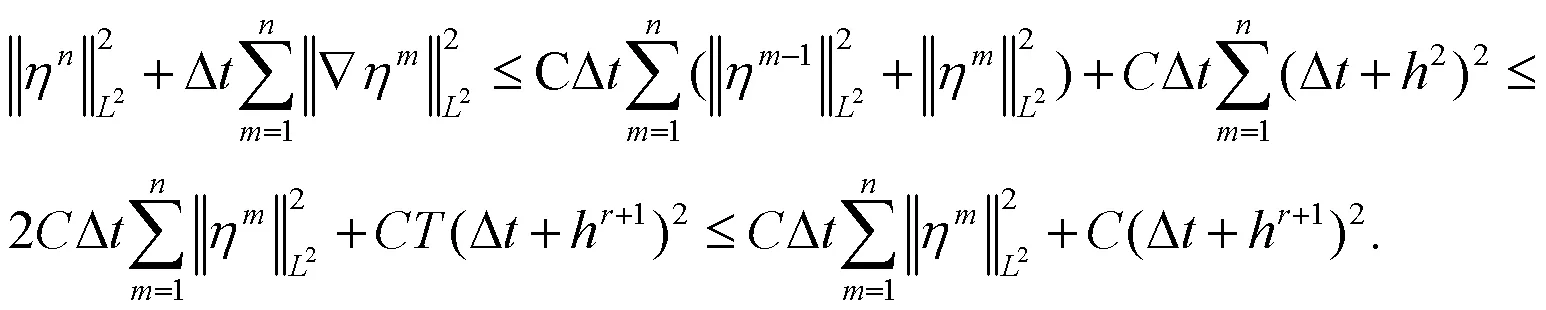
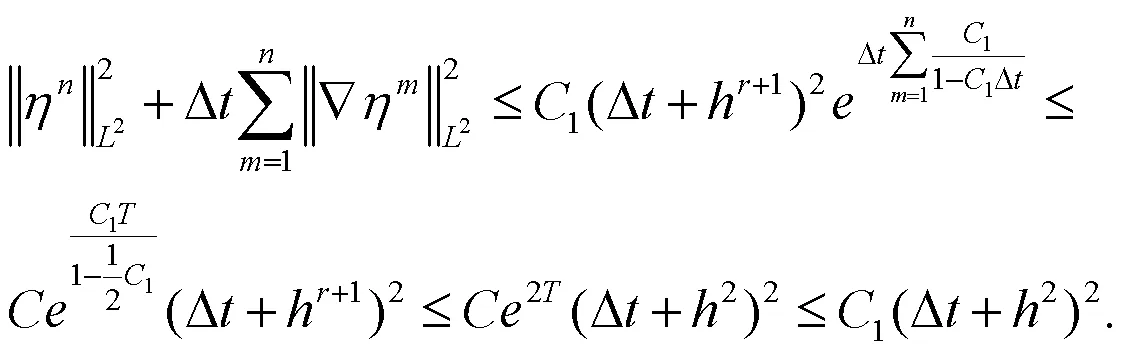
由(4)式和(5)式可得:
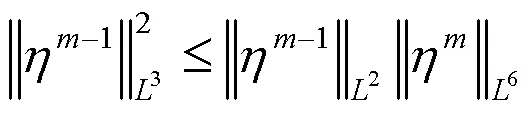
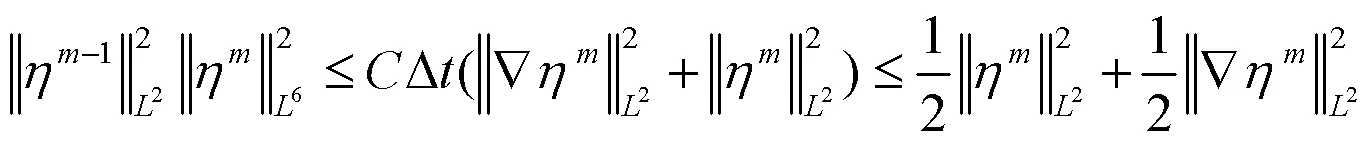
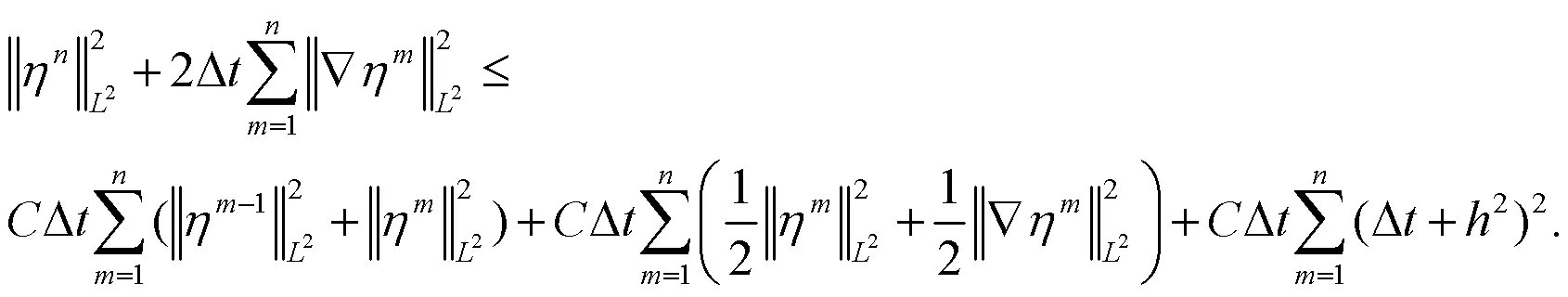
整理后可得:
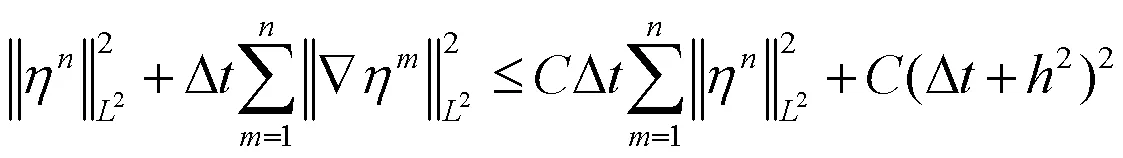
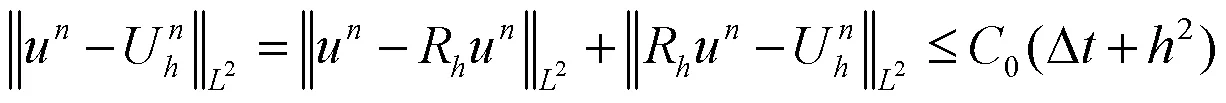
定理1得证.
[1] Kuramoto Y, Tsuzuki T. On the Formation of Dissipative Structures in Reaction-diffusion Systems [J]. Progress of Theoretical Physics, 1975, 54(3): 678-699.
[2] Akhromeeva T S, Kurdyumov S P, Malinetskii G G, et al. Classification of Solutions of a System of Nonlinear Diffusion Equations in a Neighborhood of a Bifurcation Point [J]. Journal of Soviet Mathematics, 1988, 41(5): 1292-1356.
[3] Tsertsvadze G Z. On the Convergence of Difference Schemes for the Kuramoto-Tsuzuki Equation and Reaction- diffusion Type Systems [J]. Computational Mathematics & Mathematical Physics, 1992, 31(5): 40-47.
[4] Sun Z Z. On Tsertsvadze’s Difference Scheme for the Kuramoto-Tsuzuki Equation [J]. Journal of Computational Applied Mathematics, 1998, 98(2): 289-304.
[5] Omrani K. Convergence of Galerkin Approximations for the Kuramoto-Tsuzuki Equation [J]. Numerical Methods for Partial Differential Equations, 2005, 21(5): 961-975.
[6] Wang S, Wang T, Zhang L, et al. Convergence of a Nonlinear Finite Difference Scheme for the Kuramoto-Tsuzuki Equation [J]. Communications in Nonlinear Science Numerical Simulation, 2011, 16(6): 2620-2627.
[7] Sun Z Z. A Linear Difference Scheme for the Kuramoto-Tsuzuki Equation [J]. Journal of Computational Mathematics, 1996, 14(1): 1-7.
[8] 孙志忠. 数值求解Kuramoto-Tsuzuki方程的广义Box格式[J]. 东南大学学报, 1996, 26(1): 87-92.
[9] Wang T, Guo B. A Robust Semi-explicit Difference Scheme for the Kuramoto-Tsuzuki Equation [J]. Journal of Computational and Applied Mathematics, 2009, 233(4): 878-888.
[10] Hu X, Chen S, Chang Q. Fourth-order Compact Difference Scheme for 1D Nonlinear Kuramoto-Tsuzuki Equation [J]. Numerical Methods for Partial Differential Equations, 2015, 31(6): 2080-2109.
[11] Leonaviciene T, Bugajev A, Jankeviciute G, et al. On Stability Analysis of Finite Difference Schemes for Generalized Kuramoto-Tsuzuki Equation with Nonlocal Boundary Conditions [J]. Mathematical Modelling and Analysis, 2016, 21(5): 630-643.
[12] Li B, Sun W. Error Analysis of Linearized Semi-implicit Galerkin Finite Element Methods for Nonlinear Parabolic Equations [J]. International Journal of Numerical Analysis Modeling, 2013, 10(3): 622-633.
[13] Li B, Sun W. Unconditional Convergence and Optimal Error Estimates of a Galerkin-mixed FEM for Incompressible Miscible Flow in Porous Media [J]. SIAM Journal on Numerical Analysis, 2013, 51(4): 1959-1977.
[14] Li D F. Optimal Error Estimates of a Linearized Crank-Nicolson Galerkin FEM for the Kuramoto-Tsuzuki Equations [J]. Communications in Computational Physics, 2019, 26(3): 838-854.
Optimal Error Estimates of a First-order Linearized Backward Euler FEM for the Kuramoto-Tsuzuki Equations
CUI Xuewei
(College of Mathematics and Physics, Wenzhou University, Wenzhou, China 325035)
For the high-dimensional nonlinear Kuramo-Tsuzuki equations, a first-order backward Euler finite factor is given in a fully discrete format. The semi-hidden format of nonlinear terms is used, which theoretically proves the stability of discrete solution and the unconditional optimal error estimates of discrete solution and precise solution.
First-order Backward Euler FEM; Unconditional Optimal Error Estimates; Kuramo-Tsuzuki Equation; High Dimensional Nonlinear Problem
O241.82
A
1674-3563(2022)01-0017-08
10.3875/j.issn.1674-3563.2022.01.003
本文的PDF文件可以从www.wzu.edu.cn/wzdxxb.htm获得
2020-11-26
崔雪微(1993―),女,黑龙江绥化人,硕士研究生,研究方向:偏微分方程数值解
(编辑:封毅)
(英文审校:黄璐)
