广义Birnbaum-Saunders分布
2022-03-16何慧姿
何慧姿
广义Birnbaum-Saunders分布
何慧姿
(温州大学数理学院,浙江温州 325035)
提出了广义Birnbaum-Saunders分布,完善了Birnbaum-Saunders分布.Birnbaum-Saunders分布是逆高斯分布和互补倒数的等权混合,通过将Birnbaum-Saunders分布中的逆高斯部分推广到广义逆高斯分布得到了广义Birnbaum-Saunders分布,并给出了广义Birnbaum-Saunders分布的参数的基本统计性质和极大似然估计,最后通过实际数据集说明了模型的有效性.
Birnbaum-Saunders分布;广义逆高斯分布;极大似然估计
Birnbaum-Saunders(BS)分布最初是由Birnbaum和Saunders于1969年提出的一种疲劳寿命分布[1],可用于模拟金属在周期性应力作用下的疲劳寿命.BS分布是可靠性数据分析中最常用的寿命分布之一.一个双参数BS随机变量的累积分布函数(CDF)为:
一般的推导.文献[3]于1986年研究了BS分布与逆高斯分布之间的关系,作者还证明了BS分布是逆高斯分布和互补倒数的等权混合,因此其概率密度函数(Probability Densinity Function,PDF)可以表示为:
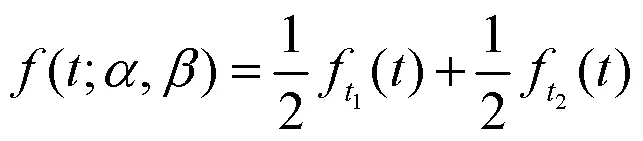
Diáz-Garciá和Leiva-Sánchez用Cauchy分布、Pearson type VII 分布、Bessel分布、Laplace分布和logistic分布等对称分布代替正态核来推广BS分布[4],Balakrishnan等对于预先确定的截断时间的寿命试验,给出了这种广义BS(Generalized Birnbaum-Saunders,GBS)分布的抽样方法[5],Leiva等讨论了这类分布的各种性质,并提出了一些推论方法[6].Kundu等提出了BS分布的双变量模型[7-8],Kundu等研究了GBS分布的多元形式[9],而Caro-Lopera等提出了矩阵变量GBS分布[10].本文主要利用BS分布的性质(1)来推广BS分布.
1953年,Good通过增加一个额外的参数(顺序)提出了逆高斯分布的推广,即广义逆高斯分布[11].Barndorff-Nielsen等于1977年首次提出了广义逆高斯分布的概念[12].广义逆高斯分布的概率密度函数为[13]:
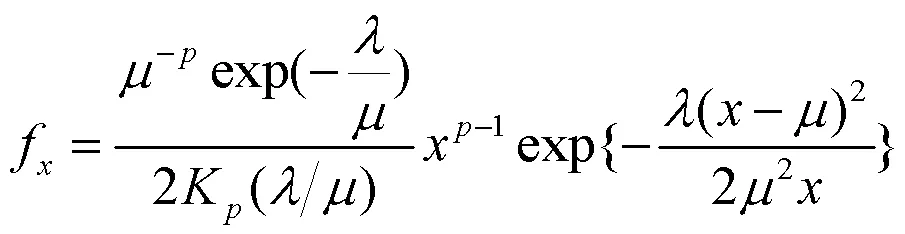
本文研究的是Birnbaum-Saunders分布的推广.由于BS分布是逆高斯分布和互补倒数的等权混合,因此我们将其中的逆高斯分布变为广义逆高斯分布,就得到了一个新的三参数的广义Birnbaum-Saunders(GBS)分布.本文介绍了GBS分布,也给出了GBS分布的分布函数、基本统计性质以及极大似然估计,并进行了数值模拟,最后,通过实际数据集说明了所给模型的有效性.
1 广义Birnbaum-Saunders分布
1.1 概率密度函数
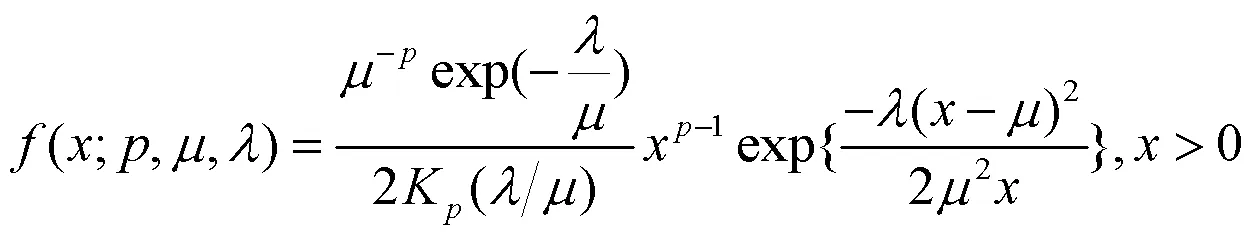
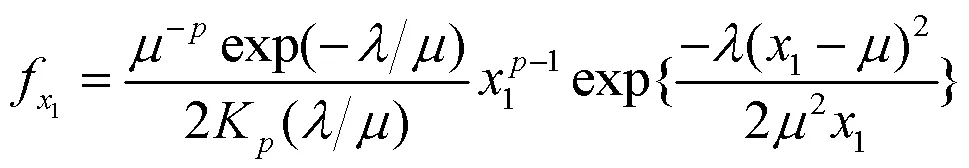
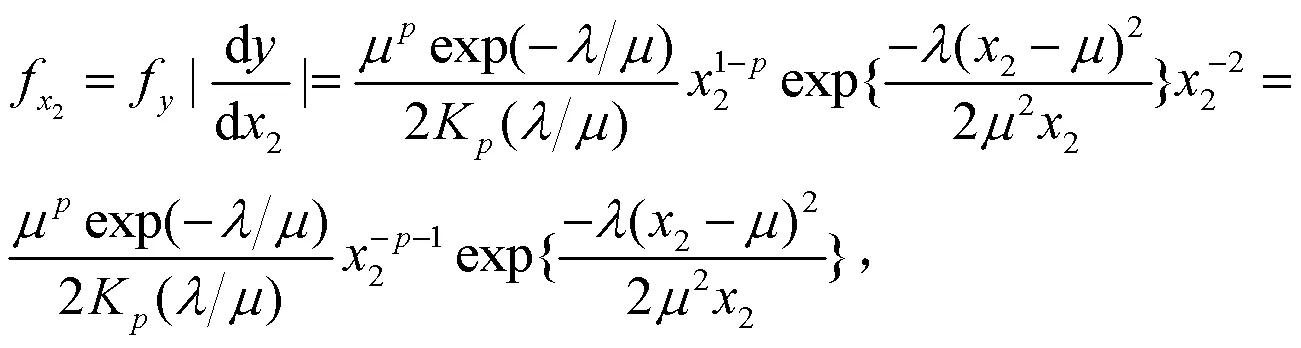
则新分布为:
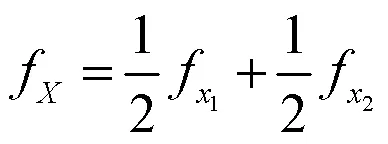
其中
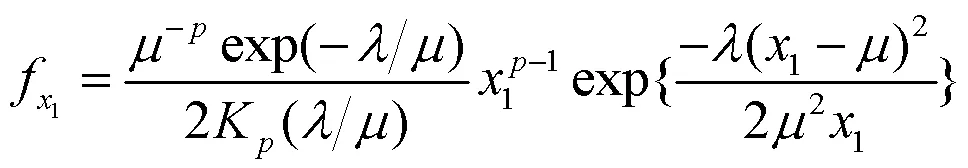
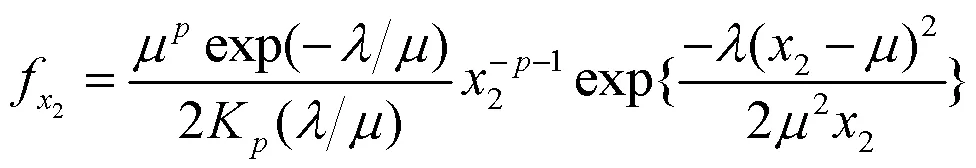
因此GBS分布的概率密度函数为:
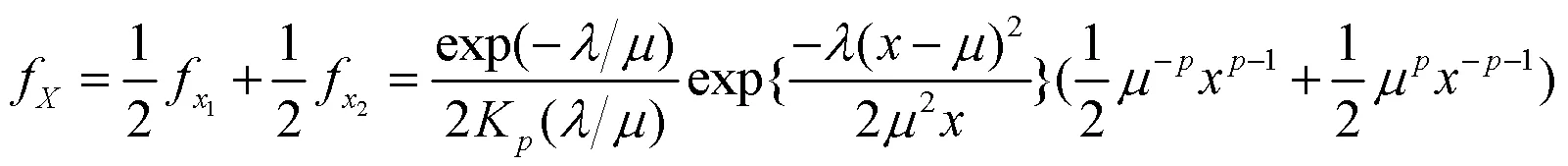
图1 GBS分布的概率密度函数
1.2 分布函数
Lemonte和Cordeiro[15]给出了广义逆高斯分布的分布函数为:
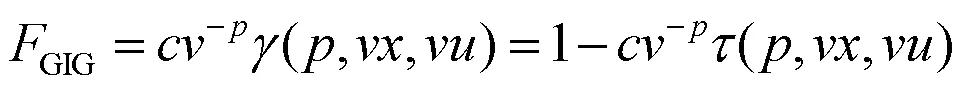
其中,
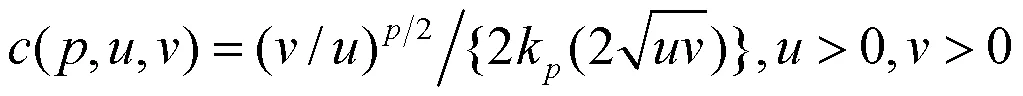
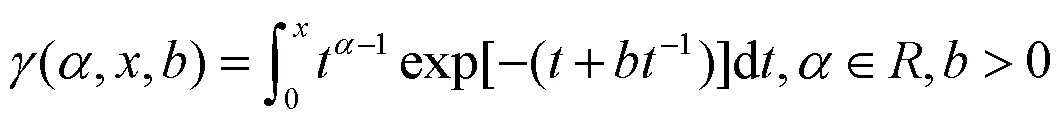
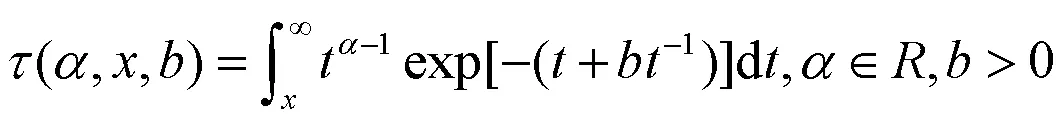
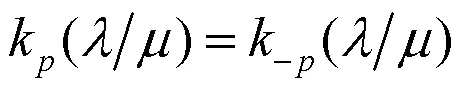
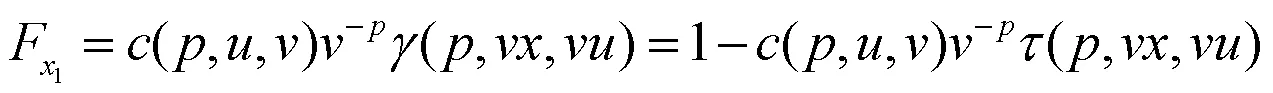
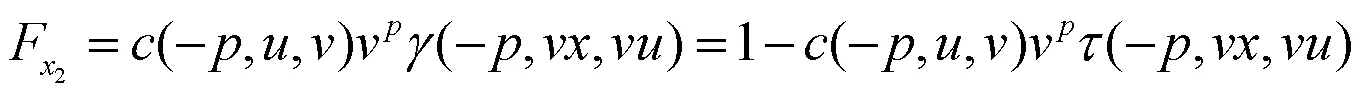
因此,此混合分布的分布函数为:
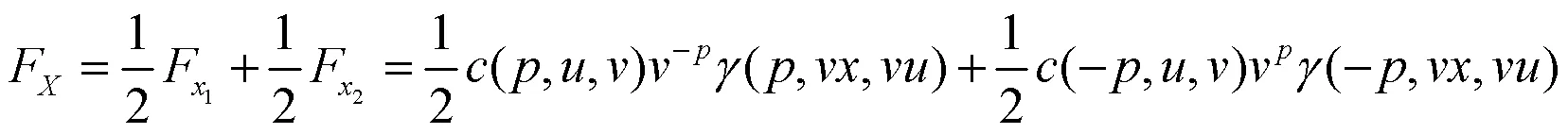
1.3 失效率函数
前文已经给出了GBS分布的概率密度函数和分布函数.根据失效率函数的定义,我们可以直接写出GBS分布的失效率函数:
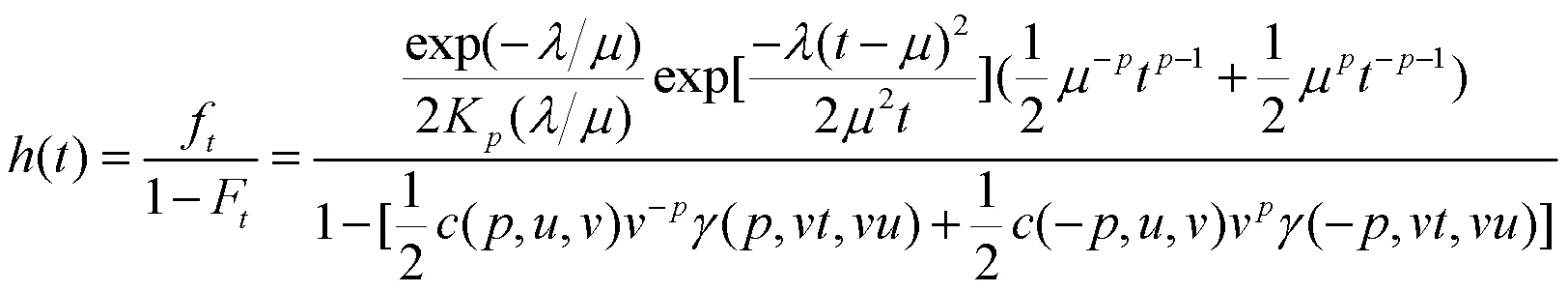
1.4 矩
计算GBS分布的矩,需要先得到广义逆高斯函数的矩,这里首先引入了第三类修正贝塞尔函数[13]:
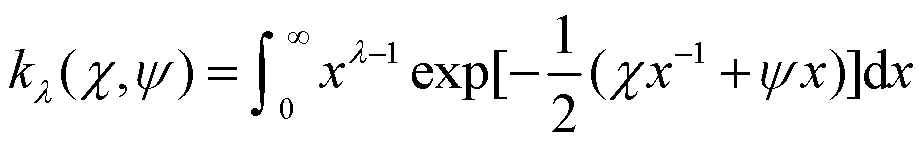
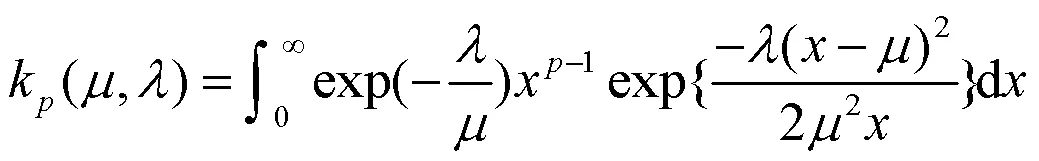

期望和方差分别为:

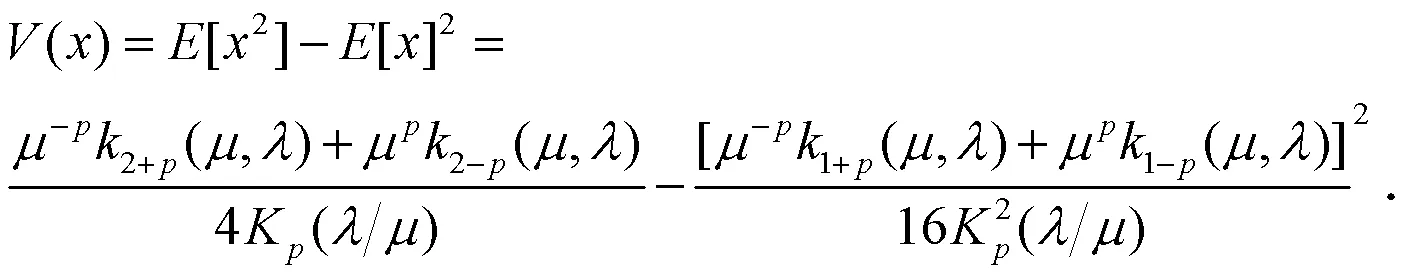
2 极大似然估计
2.1 参数点估计
同理,(5)式变为:
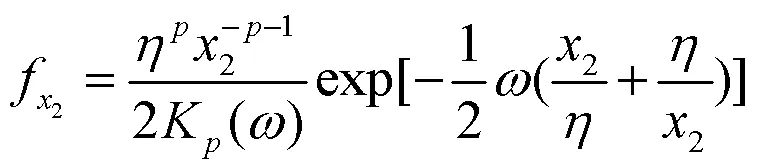
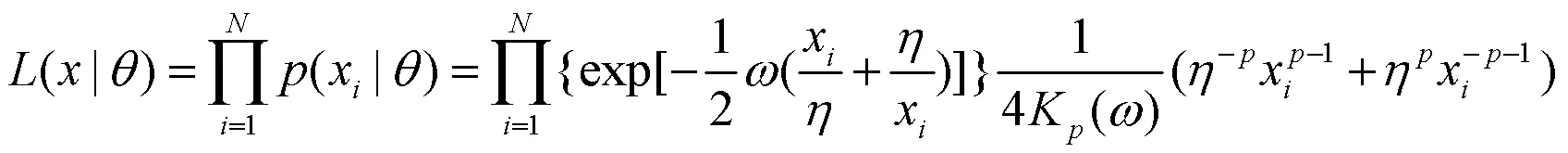
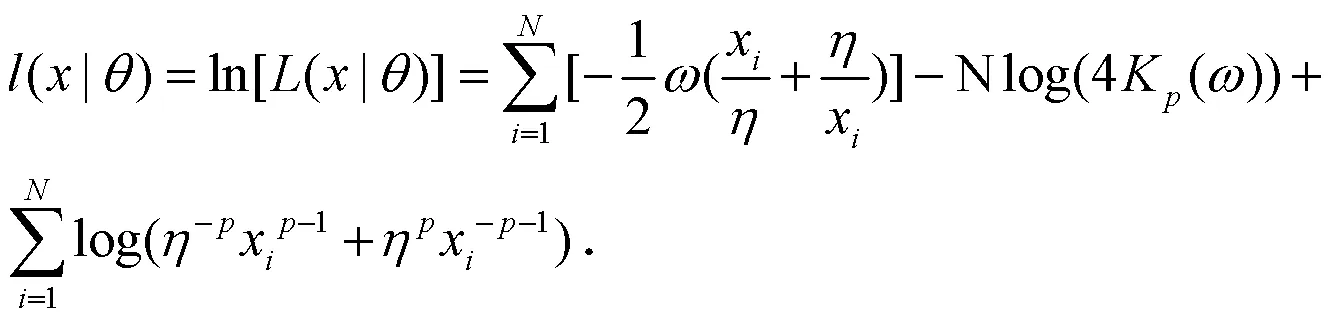
对(15)式求偏导,得各参数的偏导数分别为:
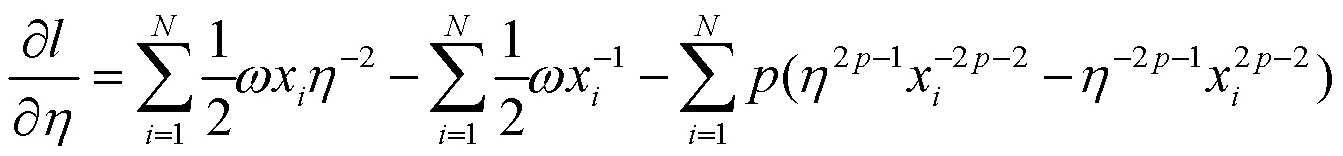
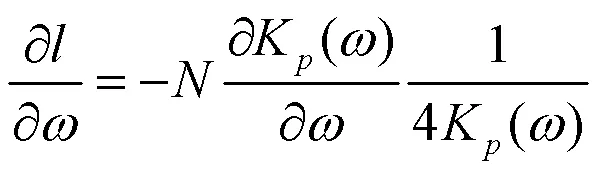
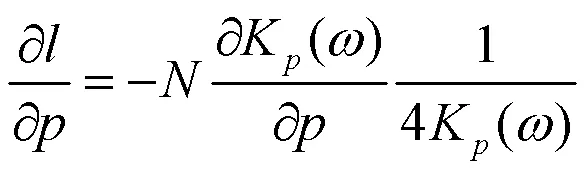
上面已经得到各参数的偏导数,令偏导数为零,便可得到3个参数的重估计公式,这里参数的重估计公式没有显示解.
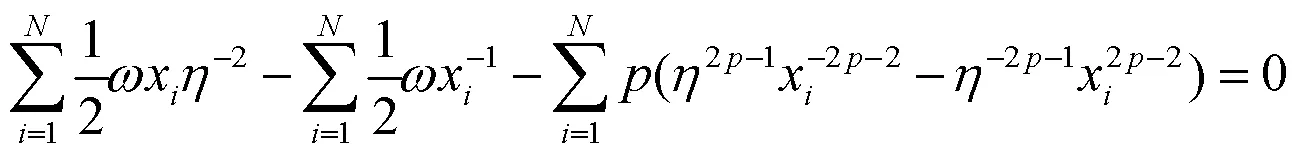
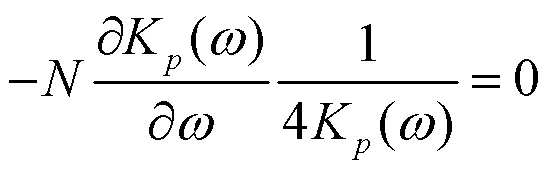
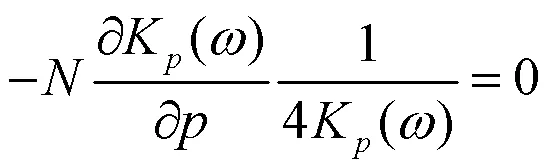
2.2 区间估计
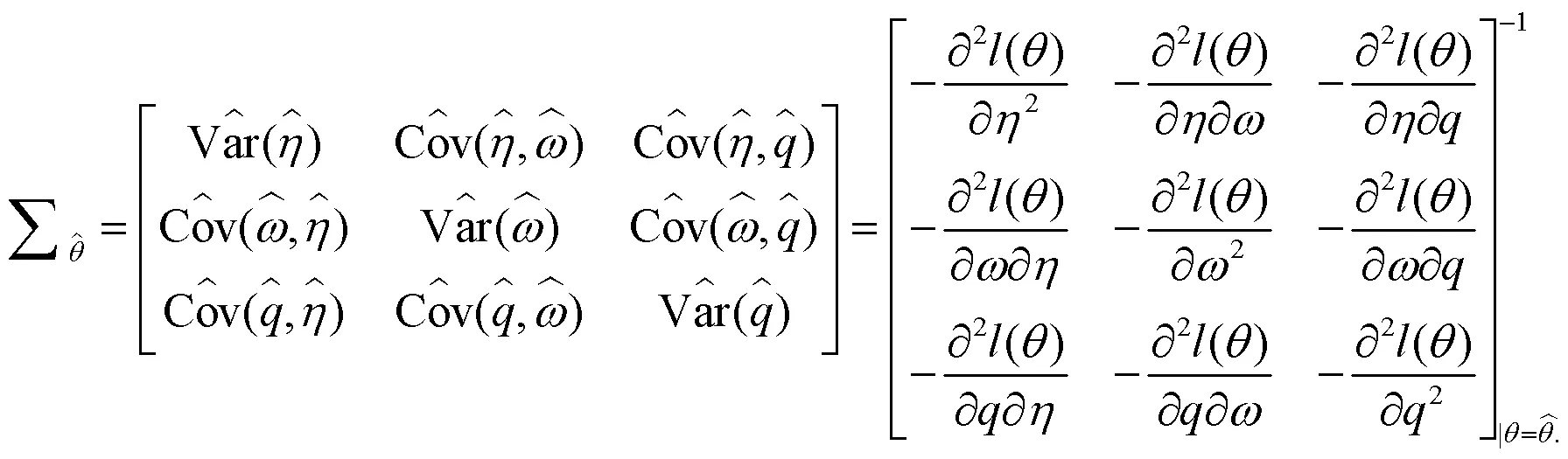
3 数值模拟

表 1 GBS分布的模拟数据参数统计描述
4 实例分析
本节将用真实数据集进行拟合,并对比GBS分布和BS分布的拟合效果.由于BS分布的起源,我们知道对于疲劳寿命数据BS分布是个很好的模型,因此本节用广义BS分布和BS分布来拟合这类数据是恰当的.首先,给出一个数据集,此数据集为空调系统连续故障的次数[15],完整的数据为:194,413,90,74,55,23,97,50,359,50,130,487,57,102,15,14,10,57,320,261,51,44,9,254,493,33,18,209,41,58,60,48,56,87,11,102,12,5,14,14,29,37,186,29,104,7,4,72,270,283,7,61,100,61,502,220,120,141,22,603,35,98,54,100,11,181,65,49,12,239,14,18,39,3,12,5,32,9,438,43,134,184,20,386,182,71,80,188,230,152,5,36,79,59,33,246,1,79,3,27,201,84,27,156,21,16,88,130,14,118,44,15,42,106,46,230,26,59,153,104,20,206,5,66,34,29,26,35,5,82,31,118,326,12,54,36,34,18,25,120,31,22,18,216,139,67,310,3,46,210,57,76,14,111,97,62,39,30,7,44,11,63,23,22,23,14,18,13,34,16,18,130,90,163,208,1,24,70,16,101,52,208,95,62,11,191,14,71.
为了将GBS分布和BS分布的拟合进行对比,这里给出了Akaike信息准则(AIC),其一般定义为:
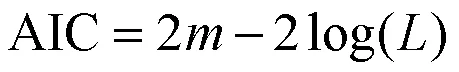

表2 GBS分布的模型参数估计和AIC

表3 BS分布的模型参数估计和AIC
图2是GBS分布和BS分布拟合的分布函数(Cumulative Density Function,CDF)图,其中黑色散点代表真实数据的经验分布函数,紫色实线和红色虚线分别代表GBS分布和BS分布拟合的CDF.
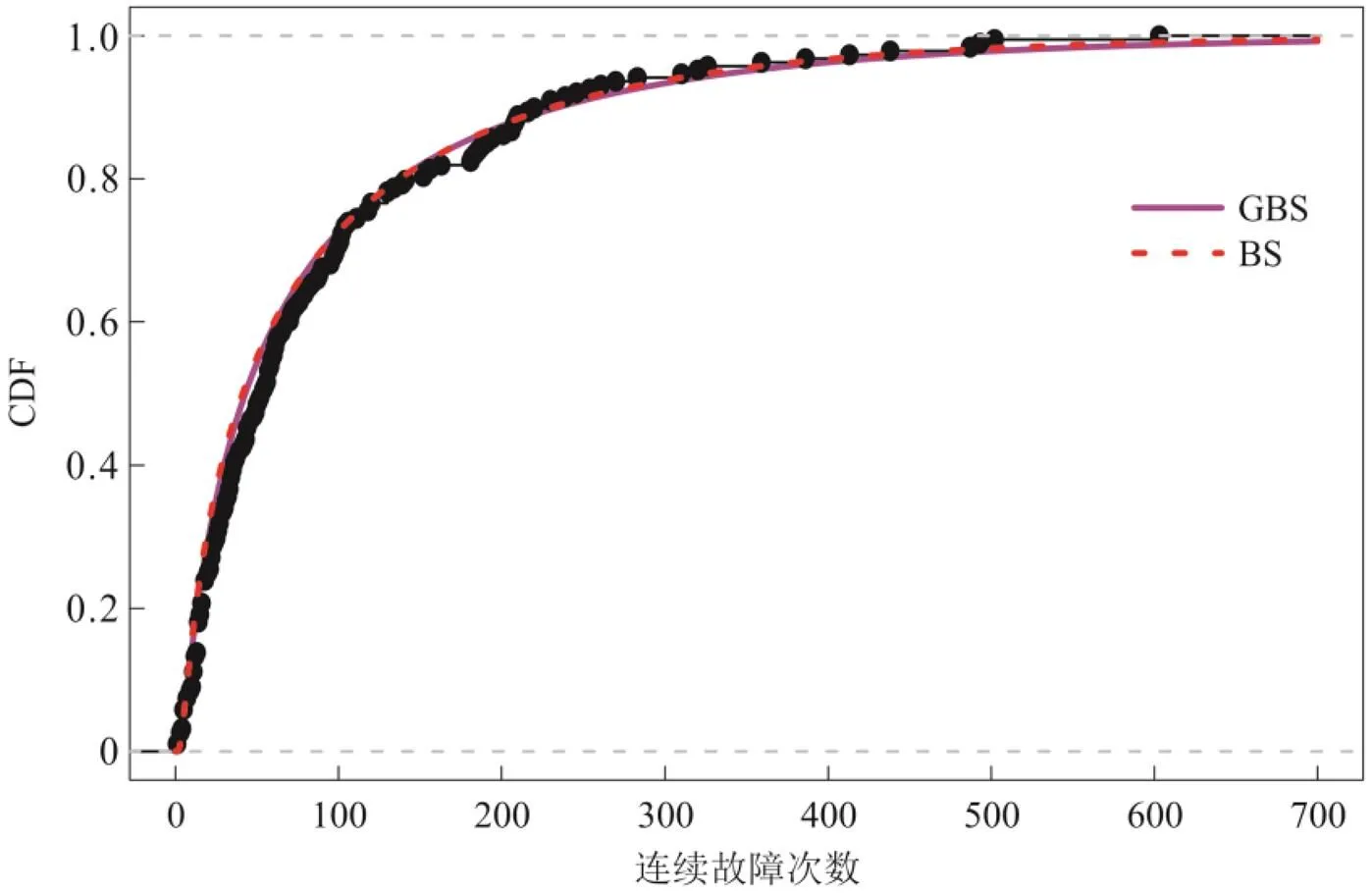
图2 GBS分布和 BS分布拟合CDF图
5 结 论
本文提出了新的广义Birnbaum-Saunders分布,完善了BS分布,给出了新分布的概率密度函数、分布函数、失效率函数、矩,也研究了模型参数的极大似然估计,并对其进行了数值模拟,最后,将新分布应用于实际数据集中,证明了该方法可以提供更好的拟合效果.
[1] Birnbaum Z W, Saunders S C. A New Family of Life Distributions [J]. Journal of Applied Probability, 1969, 6(2): 319-327.
[2] Desmond A. Stochastic Models of Failure in Random Environments [J]. Canadian Journal of Stats, 1985, 13(3): 171-183.
[3] Desmond A F. On the Relationship between Two Fatigue-life Models [J]. IEEE Transactions on Reliability, 1986, 35(2): 167-169.
[4] Diáz-Garciá J A, Leiva-Sánchez V. A New Family of Life Distributions Based on the Elliptically Contoured Distributions [J]. Journal of Statistical Planning and Inference, 2005, 128(2): 445-457.
[5] Balakrishnan N, Leiva V, Lopez J. Acceptance Sampling Plans From Truncated Life Tests Based on the Generalized Birnbaum-Saunders Distribution [J]. Communications in Statistics-Simulation and Computation, 2007, 36(3): 643-656.
[6] Leiva V, Riquelme M, Balakrishnan N, et al. Lifetime Analysis Based on the Generalized Birnbaum-Saunders Distribution [J]. Computational Statistics and Data Analysis, 2008, 52(4): 2079-2097.
[7] Kundu D, Balakrishnan N, Jamalizadeh A. Bivariate Birnbaum-Saunders Distribution and Associated Inference [J]. Journal of Multivariate Analysis, 2010, 101(1): 113-125.
[8] Vilca F, Balakrishnan N, Zeller C B. A Robust Extension of the Bivariate Birnbaum-Saunders Distribution and Associated Inference [J]. Journal of Multivariate Analysis, 2014, 124: 418-435.
[9] Kundu D, Balakrishnan N, Jamalizadeh A. Generalized Multivariate Birnbaum-Saunders Distributions and Related Inferential Issues [J]. Journal of Multivariate Analysis, 2013, 116: 230-244.
[10] Caro-Lopera F J, Leiva V, Balakrishnan N. Connection between the Hadamard and Matrix Products with an Application to Matrix-variate Birnbaum-Saunders Distributions [J]. Journal of Multivariate Analysis, 2012, 104(1): 126-139.
[11] Good I J. The Population Frequencies of Species and the Estimation of Population Parameters [J]. Biometrika, 1953, 40: 237-260.
[12] Barndorff-Nielsen O, Halgreen C. Infinite Divisibility of the Hyperbolic and Generalized Inverse Gaussian Distributions [J]. Probability Theory and Related Fields, 1977, 38(4): 309-311.
[13] Paolella M S. Intermediate Probability: A Computational Approach [M]. New Jersey: John Wiley and Sons, Ltd, 2007: 300-301.
[14] Barndorff-Nielsen O. First Hitting Time Models for the Generalized Inverse Gaussian Distribution [J]. Stochastic Processes and Their Applications, 1978, 7(1): 49-54.
[15] Lemonte A J, Cordeiro G M. The Exponentiated Generalized Inverse Gaussian Distribution [J]. Stats and Probability Letters, 2011, 81( 4): 506-517.
[16] Chaudhry M A, Zubair S M. Generalized Incomplete Gamma Functions with Applications [J]. Journal of Computational and Applied Mathematics, 1994, 55(1): 99-123.
[17] Meeker W Q, Escobar L A. Statistical Methods for Reliability Data [M]. New York: John Wiley and Sons, 1998: 186-187.
Generalized Birnbaum-Saunders Distribution
HE Huizi
(College of Mathematics and Physics, Wenzhou University, Wenzhou, China 325035)
The paper proposes the generalized Birnbaum-Saunders(GBS) distribution to extend the Birnbaum- Saunders (BS) distribution which is an equal weight mixture of the inverse Gaussian distribution and the complementary reciprocal. The GBS distribution is obtained by extending the inverse Gaussian distribution part of the BS distribution to the generalized inverse Gaussian distribution. The basic statistical properties and maximum likelihood estimation of its parameters are given and its usefulness is illustrated by means of a real data set.
Birnbaum-Saunders Distribution; Generalized Inverse Gaussian Distribution; Maximum Likelihood Estimation
O211
A
1674-3563(2022)01-0008-09
10.3875/j.issn.1674-3563.2022.01.002
本文的PDF文件可以从www.wzu.edu.cn/wzdxxb.htm获得
2020-07-27
何慧姿(1992― ),女,江西上饶人,硕士研究生,研究方向:应用统计与数理金融
(编辑:王一芳)
(英文审校:黄璐)
