输入受限下欠驱动AUV轨迹跟踪滑模控制

李鑫滨, 王 鹏, 骆 曦, 潘洪涛

输入受限下欠驱动AUV轨迹跟踪滑模控制

李鑫滨, 王 鹏, 骆 曦, 潘洪涛

(燕山大学 智能控制系统与智能装备教育部工程研究中心, 河北 秦皇岛, 066004)

针对欠驱动自主水下航行器(AUV)在外界干扰和输入受限下水平面轨迹跟踪问题, 提出了基于非线性干扰观测器和径向基函数(RBF)神经网络的滑模控制器。首先, 将欠驱动AUV运动学模型通过坐标变换转换为误差运动学模型镇定位置误差; 其次, 利用反步法设计艏摇角虚速度控制律, 镇定姿态误差; 然后采用非线性干扰观测器对时变海流扰动进行估计, 并通过滤波器估计虚拟控制律的导数, 避免了虚拟控制律求导引起的“微分爆炸”; 最后, 设计自适应RBF神经网络对欠驱动AUV实际输入进行补偿, 通过李雅普诺夫稳定性证明闭环跟踪误差所用信号一致有界。仿真验证了所设计控制器的有效性。

欠驱动自主水下航行器; 输入受限; 轨迹跟踪; 滑模控制

0 引言

随着人类科学技术的不断进步, 人们对海洋资源的开发和投入也随之增大。欠驱动自主水下航行器(autonomous undersea vehicle, AUV)由于具有更高的机动性和系统可靠性, 在海洋科学调查、水下勘探和海洋目标探查等领域中起到了重要作用[1-2]。实现AUV控制系统稳定的轨迹跟踪是确保其在水下平稳可靠工作的关键。但在实现精确而鲁棒的动态控制时, 通常会遇到2个问题: 一是如何在复杂未知外部干扰的情况下提高系统的鲁棒性[3], 这些外部干扰会严重降低闭环系统的性能; 二是如何解决执行器幅值问题导致控制效果下降甚至不稳定的问题[4]。

近年来, 模糊控制方法、滑模控制方法、反步控制方法、自适应控制方法和神经网络法等鲁棒控制方法被广泛用于AUV的运动控制中。Liang等[5]针对AUV在模型不确定性和时变干扰等复杂未知条件下轨迹跟踪问题, 提出一种自适应模糊动态面控制器(dynamic surface control, DSC)。邓非等[6]针对AUV存在洋流干扰、非线性等问题, 提出了一种基于高增益观测器的反步控制。Wang等[7]针对AUV复杂非线性问题, 提出了一种基于神经网络的自适应控制器, 但未考虑能耗和续航问题。Che等[8]考虑到在舵机故障和洋流干扰下的AUV控制问题, 提出了基于神经网络估计器的容错控制, 使闭环系统具有良好性能。Cho等[9]针对AUV跟踪控制问题, 提出了基于误差动力学的反步控制, 但是未考虑虚拟控制律“微分爆炸”问题。

此外, 由于AUV机载执行器的物理限制, 几乎所有的执行器都会受到输入非线性的影响, 控制输入受限是实际姿态控制系统的主要控制问题之一, 这可能导致控制效果下降甚至不稳定。Xia 等[10]针对AUV执行器饱和问题, 提出了基于抗饱和补偿器的滑模控制。Sarhadi等[11]提出了基于积分状态反馈的自适应控制器, 通过在积分状态反馈基础上加入抗饱和(anti-windup)补偿器解决AUV执行器受限中的饱和问题, 但设计过程复杂且未考虑外界扰动对系统稳定性的影响。Yu等[12]提出了自适应模糊控制的方法, 主要思想是将深度跟踪误差转化为仰角跟踪误差, 解决了升沉时的欠驱动结构问题。在控制回路中, 采用直接自适应模糊控制来补偿执行器受限的影响。江梦洁等[13]提出了一种基于观测器的控制器, 在轨迹跟踪误差方程基础上, 设计了一种误差信号观测器对原有跟踪误差进行近似, 通过引入一种光滑有界函数作为输入饱和条件的近似, 以及一种Nussbaum型偶函数, 设计了饱和动力学控制器实现执行器受限下AUV稳定控制。杨立平等[14]针对AUV推力饱和时控制器控制性能下降问题, 设计了一种基于抗积分饱和控制的主动容错控制方法。

基于上述文献分析, 文中进一步研究了在执行器幅值受限下欠驱动AUV的鲁棒控制。首先, 通过坐标变换, 将欠驱动AUV的模型转换为极坐标系下的误差模型, 将位置误差的镇定转换为视线误差的镇定。进一步, 针对动力学控制系统, 引入非线性干扰观测器对时变海流扰动进行估计。同时, 通过滤波器估计由反步法设计速度虚拟控制律的导数, 防止“微分爆炸”。针对执行器幅值未知设计自适应径向基函数(radial basis function, RBF)神经网络进行补偿, 通过Lyapunov稳定性理论分析闭环系统的稳定性, 证明跟踪误差的有界稳定, 通过仿真对比验证所提控制器的有效性。

该文的主要贡献体现在以下几方面:

1) 通过采用非线性干扰观测器对时变海流扰动进行估计, 降低了由扰动引起的滑模控制器抖振;

2) 利用反步法设计艏摇角速度虚拟控制律, 并采用滤波器求解虚拟控制律的导数, 避免了虚拟控制律求导引起的“微分爆炸”;

3) 设计自适应RBF神经网络滑模控制器, 基于稳定性理论构建自适应律并通过反馈回路对执行器实际输入偏差进行补偿, 解决了输入受限问题。

1 欠驱动AUV模型

欠驱动系统是指独立控制输入少于系统自由度的一类非线性系统。欠驱动AUV因其质量轻、惯性小、系统成本低且其驱动受多驱动装置协同作用具有较高容错率等优点受到国内外广泛关注[15]。欠驱动系统往往伴随着高度耦合和非线性等问题, 使得对欠驱动AUV的轨迹跟踪具有一定难度和局限性。欠驱动AUV在水平面不能完成水平横移和横滚运动[16]。

使用体坐标系和惯性坐标系描述欠驱动AUV水平面轨迹跟踪(见图1), 可将其描述为运动学模型和动力学模型。

图1 水平面轨迹跟踪示意图

根据牛顿-欧拉方程和拉格朗日方程推导, 欠驱动AUV动力学模型可以描述[10]为

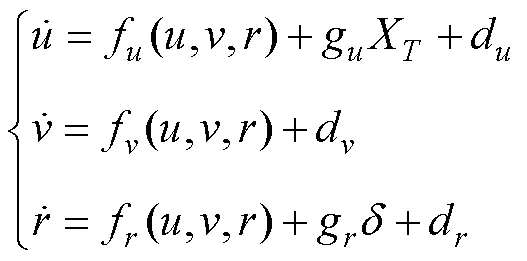
为了便于控制器设计, 做出如下假设:

1) 所有给定参考信号有界且可导, 并且其导数也有界。

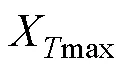
2 欠驱动AUV跟踪控制器设计

在控制器设计中充分考虑洋流扰动和执行器输入受限对系统稳定的影响, 分别针对运动学模型和动力学模型设计控制器, 控制器的设计如图2所示。采用基于视线制导律和虚速度的控制策略, 首先, 通过惯性坐标系下位置和姿态误差转换为体坐标系下的位置和姿态误差, 设计视线制导律镇定位置误差, 虚速度镇定欠驱动AUV的姿态误差, 并用虚速度作为AUV的期望速度设计控制器, 采用滤波器对设计的虚速度进行滤波处理, 解决“微分爆炸”; 再设计干扰观测器对时变的洋流扰动进行估计, 然后基于RBF神经网络和积分滑模控制方法设计动力学控制律, 使AUV的速度达到期望值, 最后, 使欠驱动AUV跟踪上期望轨迹, 并且满足系统稳定。

图2 欠驱动AUV仿真控制系统框图

2.1 运动学控制律设计

构造Lyapunov函数

设计虚拟控制律

将所设计的制导律代入式(8)可得

定义艏摇角度误差为

构造Lyapunov函数

式中,2为大于0的待设计参数。

2.2 动力学控制律设计

在运动学控制中, 由艏摇角制导律和艏摇角虚速度控制律通过镇定位置误差和姿态误差, 使欠驱动AUV跟踪期望轨迹。但是速度变量不能直接控制, 需要动力学控制器驱动AUV才能跟踪上期望速度, 因此, 将分别针对洋流和输入受限下动力模型设计艏摇角速度跟踪控制器和浪涌速度跟踪控制器, 通过引入干扰观测器对外界干扰进行估计, 针对执行器幅值未知设计自适应神经网络滑模控制器。

1) 艏摇角速度跟踪控制

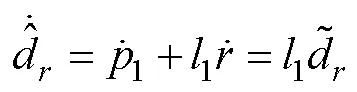
考虑到AUV易受到水下温度、压力等环境因素的影响, 会使系统某些参数改变而出现幅值未知的情况, 致使未知。通过设计自适应神经网络滑模控制器, 实现对执行器输入受限下的欠驱动AUV控制。其闭环示意图如图3所示。

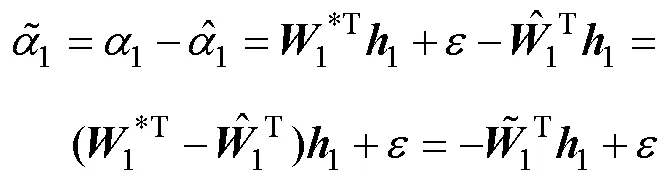
定义艏摇角速度跟踪误差为

定义滤波误差的导数为

由式(31)可知, 偏航舵角等效控制律中包含艏摇角虚速度控制律的导数、执行器幅值受限项和洋流扰动项。文中设计了干扰观测器以降低洋流扰动对欠驱动AUV控制系统稳定的影响, 采用滤波器降低了艏摇角虚速度直接求导计算的复杂度, 并且针对执行器输入受限设计了自适应神经网络的滑模控制器。此外, 为降低滑模控制的抖振, 采用饱和函数代替符号函数sgn()。

选取Lyapunov函数

设计基于滑模面的自适应律为

选取Lyapunov函数

根据Young’s不等式, 可得

则有

2) 浪涌速度跟踪控制

同样, 通过神经网络RBF估计为

定义浪涌速度误差为

设计如下滤波器估计

同样设计神经网络权值自适应律为

选取Lyapunov函数

根据Young’s不等式, 可得

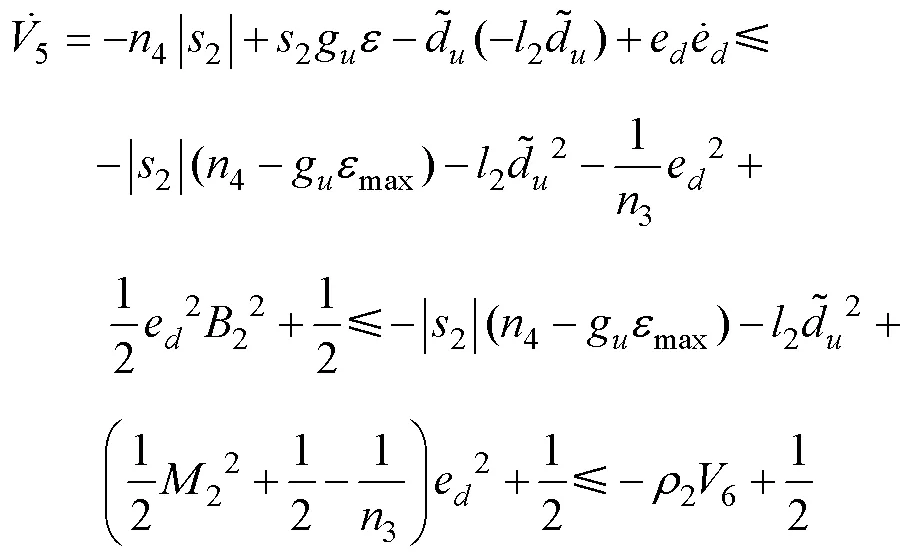
3 仿真验证

为了更好地体现文中设计控制器的有效性, 采用仿真验证所提轨迹跟踪控制器的有效性和鲁棒性。在著名的REMUS AUV上进行了数值仿真, AUV模型的参数如表1所示。

表1 AUV模型参数

在仿真验证过程中, 选取了直线轨迹跟踪和曲线轨迹跟踪。

直线轨迹为

图4 坐标跟踪曲线

图5 位置跟踪误差曲线

图6 欠驱动AUV速度跟踪曲线

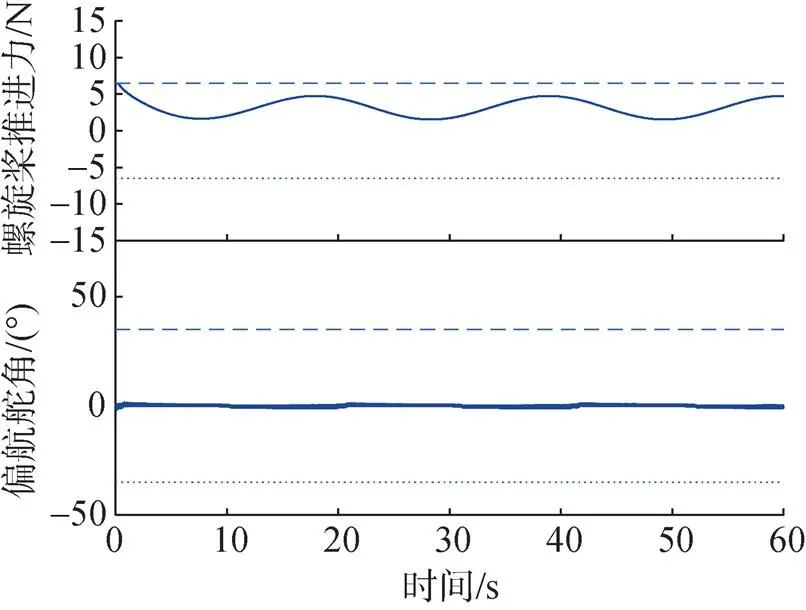
图7 推进力和偏航舵角曲线

曲线跟踪轨迹设定为

图8和图9分别为欠驱动AUV坐标的跟踪曲线和正弦轨迹跟踪曲线, 由仿真结果可以明显看出, 未考虑输入受限的控制器和考虑输入受限所设计的控制器都能完成实现欠驱动AUV正弦轨迹的跟踪, 但是在曲率较大的地方, 未考虑输入受限的控制器跟踪误差较大。

图8 正弦轨迹跟踪曲线

图10中欠驱动AUV的位置和艏摇角跟踪误差能很快收敛到零点附近, 达到渐近稳定, 但是由于扰动和输入受限的影响, 文中设计的控制器收敛速度更快且位姿误差更小。

图11给出了欠驱动AUV速度误差曲线。由仿真结果可以看出, 未考虑输入受限的控制器和考虑输入受限所设计的控制器都能收敛到理想速度, 但是文中设计的控制器的浪涌速度能更快收敛到理想速度且更为平缓, 艏摇角速度抖动幅度小且跟踪精度高。

图9 坐标跟踪曲线

图10 位置跟踪误差曲线

图11 欠驱动AUV速度误差跟踪曲线

图12和图13为控制输入的推进力、偏航舵角和神经网络补偿的曲线以及局部放大图。从图12仿真结果可以看出, 考虑输入受限下的推进力和偏航舵角能够稳定在预定范围并且具有更平滑更快的响应速度。从图13的仿真的结果可以看出, 文中所设计的自适应神经网络有较好的补偿效果, 从而有效的解决了控制输入受限的问题。

图12 推进力和偏航舵角曲线

图13 神经网络逼近曲线

4 结束语

针对AUV存在外界干扰和输出受限影响下的控制问题, 提出了基于干扰观测器和神经网络的滑模控制器。该控制器通过神经网络补偿控制输入受限, 使得AUV控制器的输入保持在既定的边界内, 提高了跟踪精度, 得到了理想的跟踪效果。仿真结果表明, 所设计的控制器能够实现AUV在水平面上的稳定跟踪控制。下一步的工作将针对欠驱动AUV在三维空间中的跟踪控制, 并对所设计的控制器进行相应的实验验证, 从而更好地说明所设计控制器的有效性和鲁棒性。

[1] Johnsen G, Ludvigsen M, Sørensen A, et al.The Use of Underwater Hyperspectral Imaging Deployed on Remotely Operated Vehicles-methods and Applications[J].IFAC Papers Online, 2016, 49(23): 476-481.

[2] Li Z, Yang C, Ding N, et al.Robust Adaptive Motion Control for Underwater Remotely Operated Vehicles with Velocity Constraints[J].International Journal of Control Automation & Systems, 2012, 10(2): 421-429.

[3] Zhang G C, Huang H, Qing H D, et al.A Novel Adaptive Second Order Sliding Mode Path Following Control for a Portable AUV[J].Ocean Engineering, 2018, 151: 82-92.

[4] 熊华胜, 边信黔, 施小成.积分变结构控制原理在AUV航向控制中的应用仿真[J].船舶工程, 2005(5): 30-33.

[5] Liang X, Qu X, Wang N, et al.Three-Dimensional Trajectory Tracking of an Underactuated AUV Based on Fuzzy Dynamic Surface Control[J].IET Intelligent Transport Systems, 2019, 14(5): 364-370.

[6] 邓非, 尹洪东, 段梦兰.基于AUV轨迹追踪的优化UKF算法[J].船舶工程, 2018, 40 (S1): 206-211, 229.

[7] Wang L L, Pan L X.Adaptive Variable Structure Control with Neuron for Path Tracking of Beaver AUV[J].IEEE Access, 2020, 8: 48566-48575.

[8] Che G, Zhen Yu.Neural-network Estimators Based Fault- tolerant Tracking Control for AUV via ADP with Rudders Faults and Ocean Current Disturbance[J].Neurocomputing, 2020, 411: 442-454.

[9] Cho G R, Park D G, Kang H, et al.Horizontal Trajectory Tracking of Underactuated AUV Using Backstepping Approach[J].IFAC-Papers Online, 2019, 52(16): 174-179.

[10] Xia Y, Xu K, Li Y, et al.Improved Line-of-sight Trajectory Tracking Control of Under-actuated AUV Subjects to Ocean Currents and Input Saturation[J].Ocean Engineering, 2019, 174(15): 14-30.

[11] Sarhadi P, Noei A R, Khosravi A.Adaptive Integral Feedback Controller for Pitch and Yaw Channels of an AUV with Actuator Saturations[J].Isa Transactions, 2016, 65: 284-295.

[12] Yu C, Xiang X, Zhang Q, et al.Adaptive Fuzzy Trajectory Tracking Control of an Under-Actuated Autonomous Underwater Vehicle Subject to Actuator Saturation[J].International Journal of Fuzzy Systems, 2018, 20(1): 269-279.

[13] 江梦洁, 李家旺, 吕艳芳, 等.饱和输入限制下欠驱动自主水下航行器水平面轨迹跟踪控制[J].兵工学报, 2017, 38(11): 2207-2213.

Jiang Meng-jie, Li Jia-wang, Lü Yan-fang, et al.Path Tracking Control of Underactuated Autonomous Underwater Vehicles on Horizontal Plane within Input Saturation Limit[J].Acta Armamentarii, 2017, 38(11): 2207- 2213.

[14] 杨立平, 张铭钧, 褚振忠, 等.水下机器人抗积分饱和控制及主动容错控制方法[J].哈尔滨工程大学学报, 2010, 31(6): 755-761.

Yang Li-ping, Zhang Ming-jun, Chu Zhen-zhong, et al.Anti-windup Control and Active Fault Tolerant Control Methods for Autonomous Underwater Vehicles[J].Journal of Harbin Engineering University, 2010, 31(6): 755-761.

[15] 王芳, 万磊, 李晔, 等.欠驱动AUV的运动控制技术综述[J].中国造船, 2010, 51(2): 227-241.

Wang Fang, Wan Lei, Li Ye, et al.A Survey on Development of Motion Control for Underactuated AUV[J].Shipbuilding of China, 2010, 51(2): 227-241.

[16] Sarhadi P, Noei A R, Khosravi A.Adaptive Integral Feedback Controller for Pitch and Yaw Channels of an AUV with Actuator Saturations[J].ISA Trans, 2016, 65: 284-295.

[17] Fossen T I.Guidance and Control of Ocean Vehicles[M].New York: John Wiley & Sons Inc, 1994.

Underactuated AUV Trajectory Tracking Sliding Mode Control with Input Limitation

LI Xin-bin, WANG Peng, LUO Xi, PANG Hong-tao

(Engineering Research Center of the Ministry of Education for Intelligent Control System and Intelligent Equipment, Yanshan University, Qinhuangdao 066004, China)

Aiming at the horizontal plane trajectory tracking problem of the underactuated autonomous undersea vehicle (AUV) under external interferences and limited inputs, a sliding mode controller based on a nonlinear disturbance observer and radial basis function(RBF) neural network was proposed in this study.Firstly, the underactuated AUV kinematics model was transformed into an error kinematics model to stabilize the position error through a coordinate transformation.Secondly, the backward step method was used to design the bow-rocking angle virtual velocity control law to stabilize the attitude error.Subsequently, a nonlinear disturbance observer was used to estimate the disturbance of a time-varying ocean current, and the derivative of the virtual control law was estimated through a filter to avoid the “differential explosion” caused by the derivative of the virtual control law.Finally, an adaptive RBF neural network was designed to compensate the actual input of the underactuated AUV, and the Lyapunov stability proved that the signal used for the closed-loop tracking error was uniformly bounded.The simulation verified the effectiveness of the designed controller.

underactuated autonomous undersea vehicle; input limitation; trajectory tracking; sliding mode

李鑫滨, 王鹏, 骆曦, 等.输入受限下欠驱动AUV轨迹跟踪滑模控制[J].水下无人系统学报, 2022, 30(1): 44-53.

TJ630.1; TB71.2

A

2096-3920(2022)01-0044-10

10.11993/j.issn.2096-3920.2022.01.006

2021-03-29;

2021-06-04.

国家自然科学基金项目资助(61873224); 河北省省级科技计划项目资助(F2020203037).

李鑫滨(1969-), 男, 博士, 教授, 主要研究方向为水下机器人智能控制.

(责任编辑: 许 妍)