可变抽样区间和样本容量的非正态EWMA控制图经济设计
2022-03-15李聪凯贾元忠
薛 丽, 李聪凯, 贾元忠
(1.郑州航空工业管理学院 管理工程学院,河南 郑州 450046; 2.天津大学 管理与经济学部,天津 300072)
0 引言
在生产制造过程中,统计过程控制是提高产品过程质量的一种有效方法,控制图作为过程控制的一种重要工具在生产实践中得到广泛应用。为了提高控制图的监控效率,许多学者研究了抽样区间变化(VSI)、样本容量变化(VSS)以及抽样区间和样本容量均变化(VSSI)的动态控制图,研究结果表明动态控制的监控效果均优于静态控制图。当监控过程中的较小波动时,Saccucci[1]设计了正态分布情形下抽样区间变化的EWMA控制图,利用马尔科夫链方法得到了双边VSI EWMA控制图的平均报警时间;吉明明等[2]研究了质量特性值服从非正态分布时的可变抽样区间EWMA均值控制图。薛丽[3]研究了过程不合格品率服从二项分布时,可变抽样区间EWMA控制图。Tang[4]等研究了监控过程均值变化时,可变抽样区间的自适应EWMA控制图。Tran[5]等研究了考虑测量误差下的可变抽样区间EWMA控制图。上面研究聚焦于可变抽样区间EWMA控制图的设计,当抽样区间和样本容量同时变化时, Reynolds[6]等研究了VSSI EWMA控制图的监控性能。他们的研究是建立在观测值服从正态分布的假设背景下,然而在实际中这一假设可能得不到满足,有时观测值会呈现偏态性[7]。当过程观测值不满足正态性假设时,一些学者[2,8]利用Burr分布近似不同情况的非正态分布进行研究。
上述研究是基于控制图的统计特性,没有考虑控制图在监控过程时产生的费用成本。为了降低过程控制时的费用成本, Lorenzen & Vance 于1986年[9]提出了控制图经济设计的统一方法。随后许多学者对动态控制图进行了经济设计。Chou等[10]针对质量特性值服从正态分布的情况下,研究了可变抽样区间EWMA控制图的经济设计。Chen[8]对可变抽样区间非正态均值控制图进行了经济设计。薛丽[12,13]分别研究了可变抽样区间几何EWMA控制图的经济设计以及监控均值标准差的VSI EWMA图经济设计。上面对于动态EWMA控制图的经济设计多集中在可变抽样区间控制图,较少考虑到非正态分布情形下可变抽样区间和样本容量的EWMA控制图。为了提高监控过程效率的同时使过程控制成本降低,本文利用Burr分布近似不同情况下的非正态分布,对可变抽样区间和样本容量的非正态EWMA控制图进行经济设计研究。
1 VSSI非正态EWMA控制图
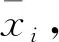
(1)
其中,λ为平滑系数,Z0=μ0。
控制图的上下控制限分别为:
(2)
其中,k是控制限系数。
控制图的上下警戒限分别为:
(3)
其中,w是警戒限系数。
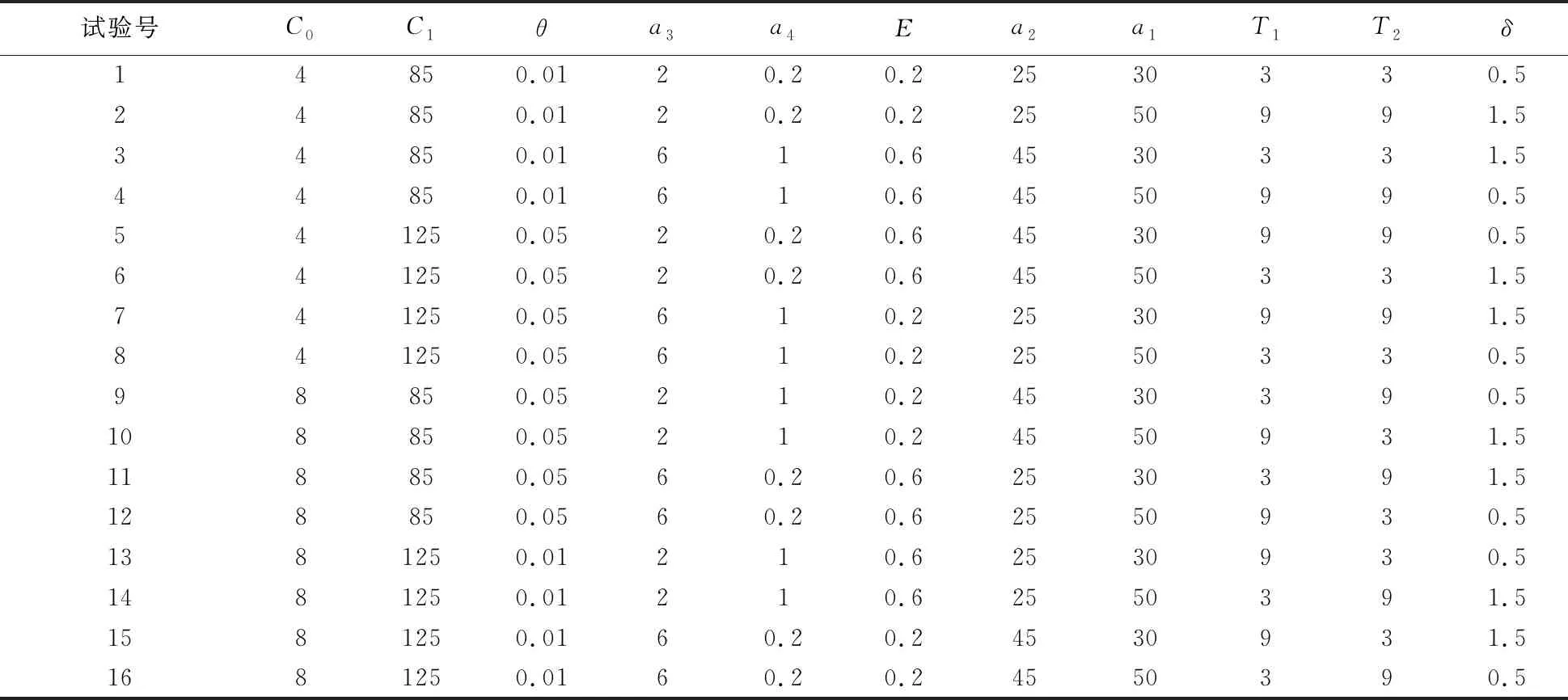
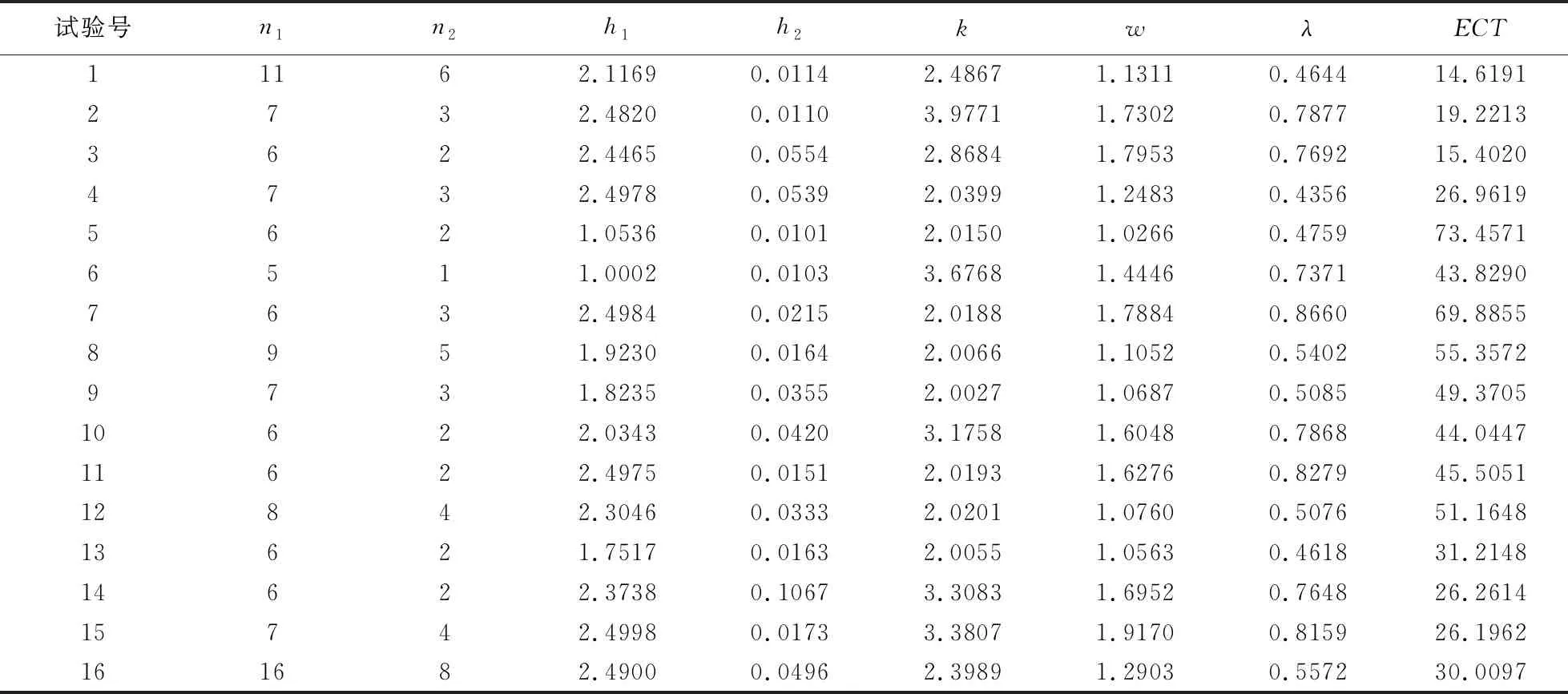
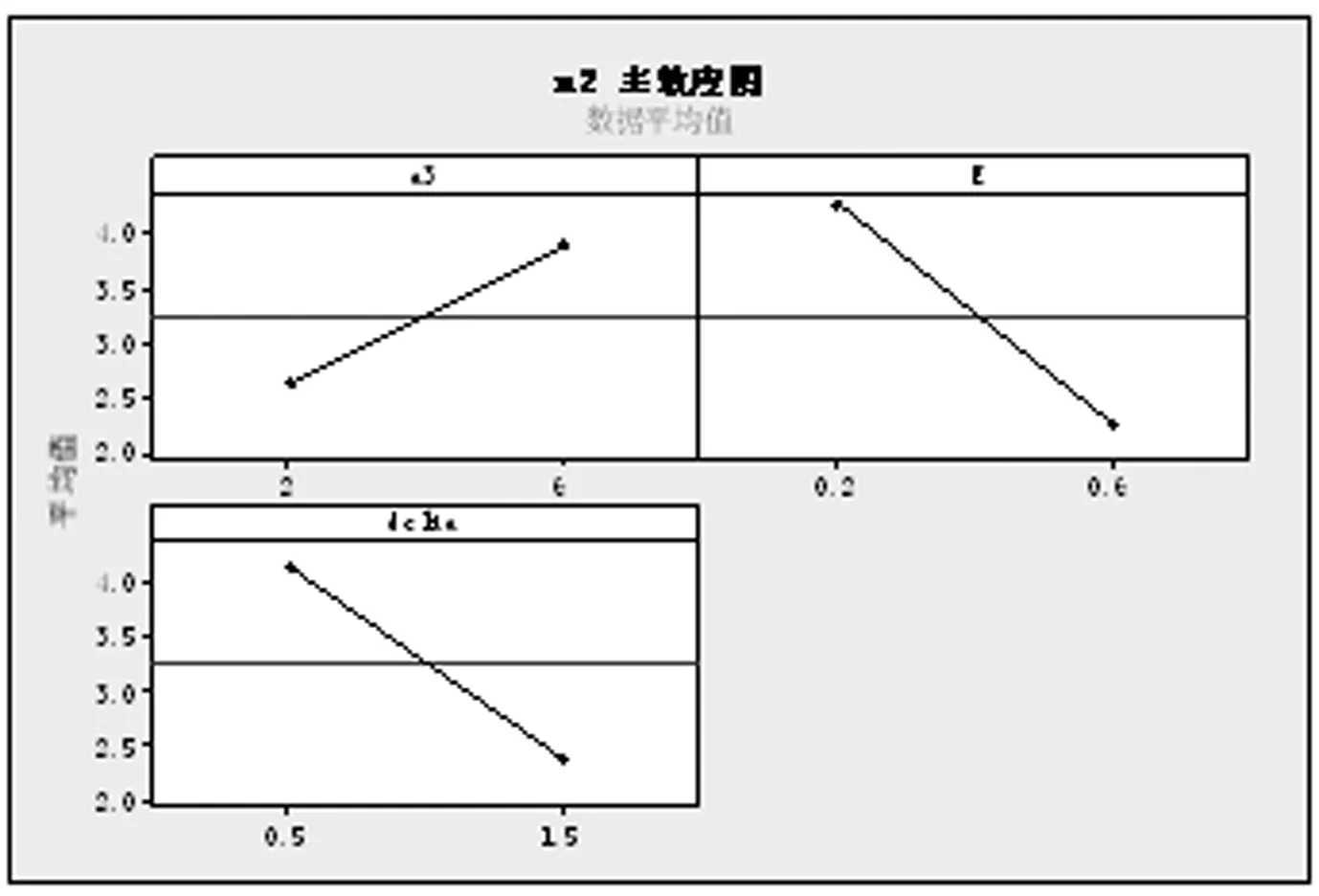
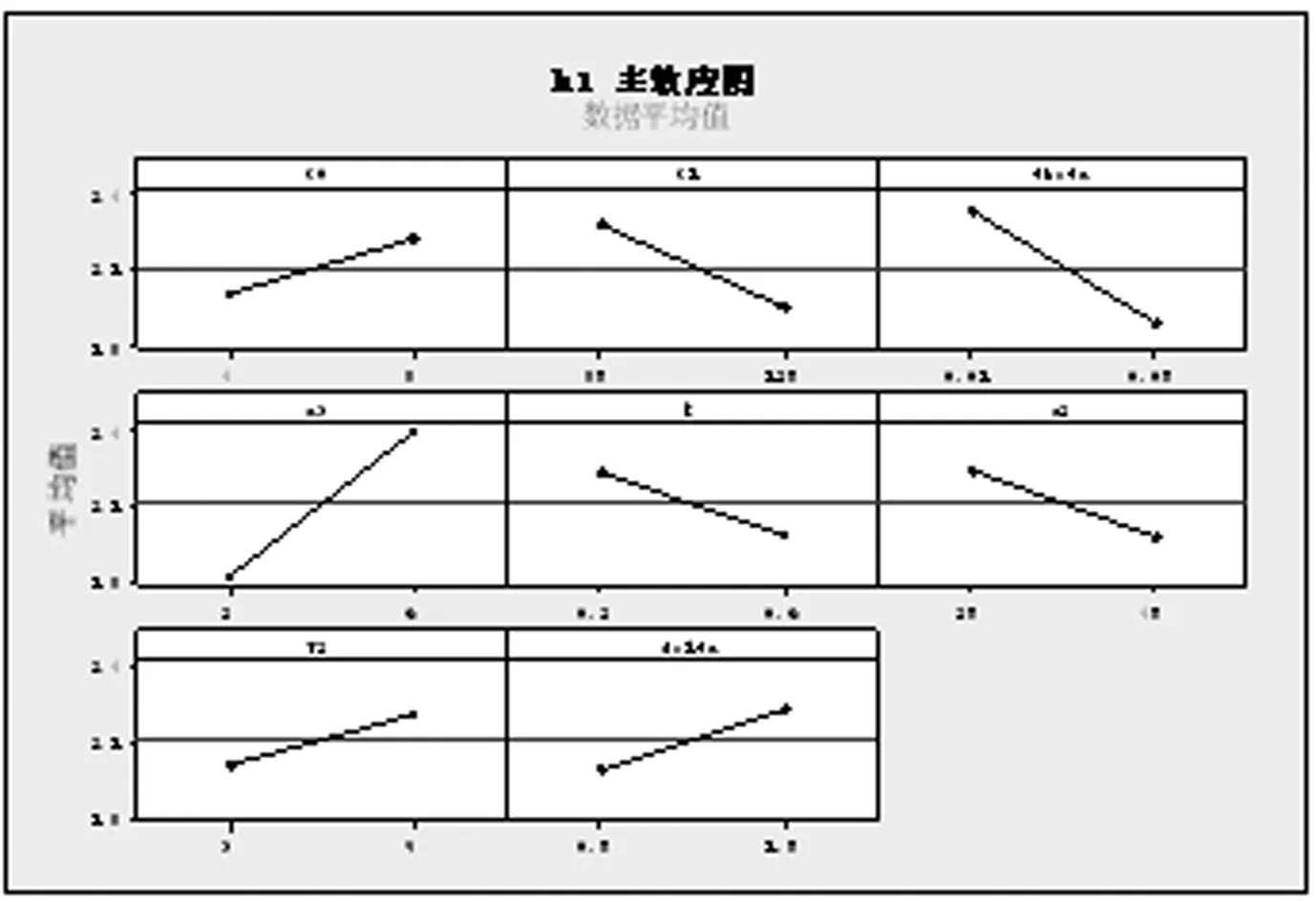
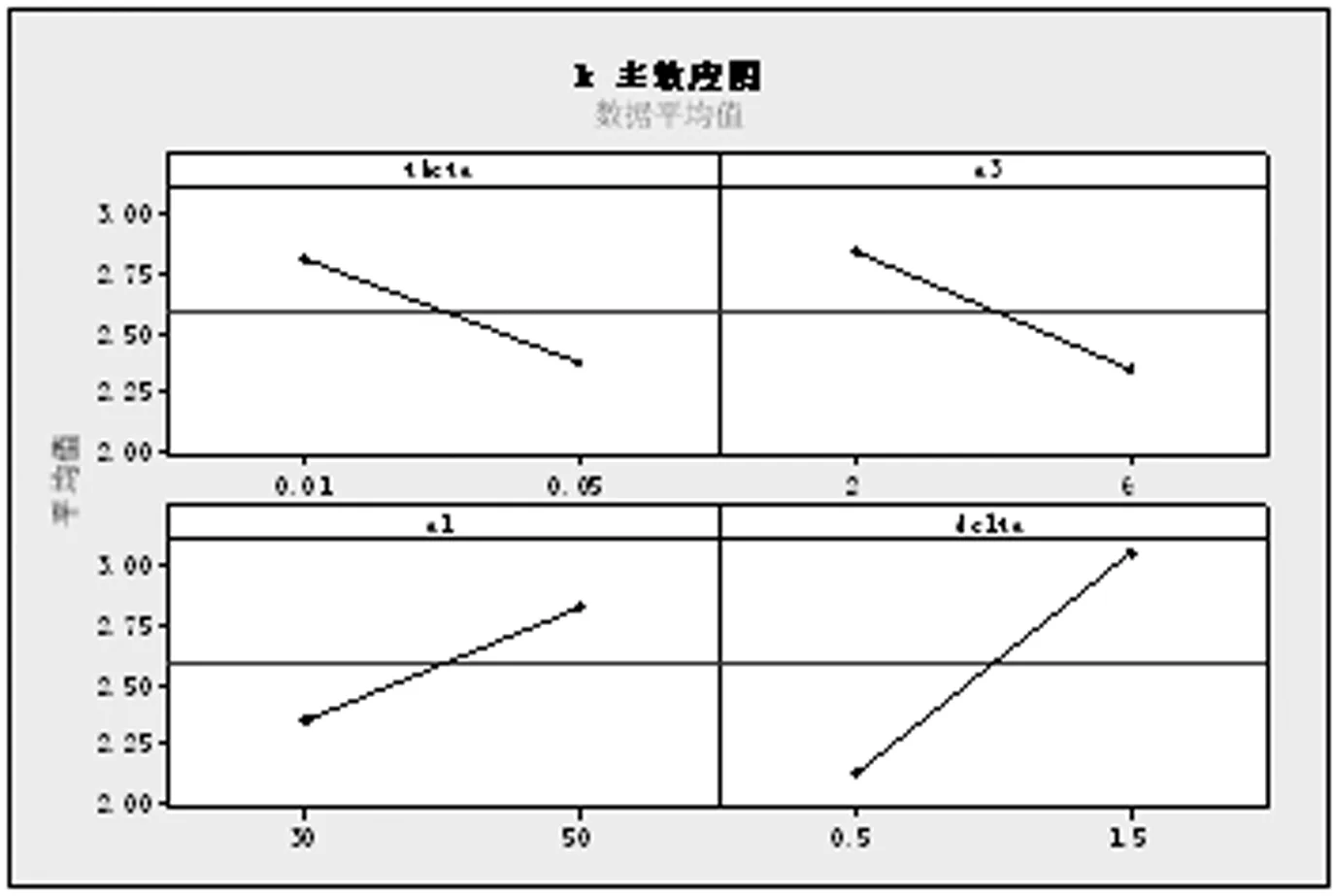
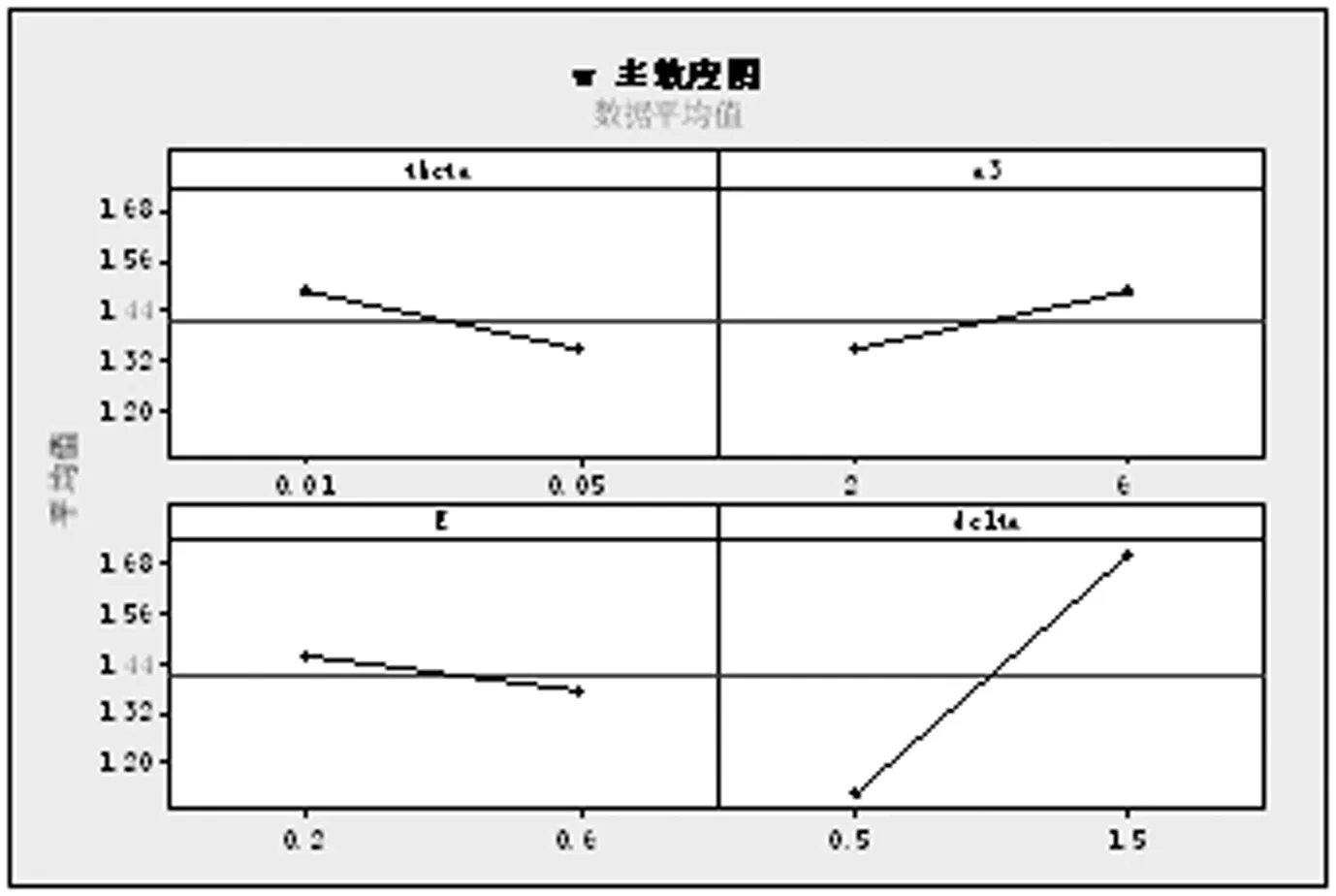
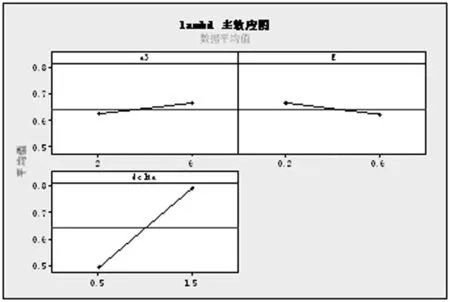
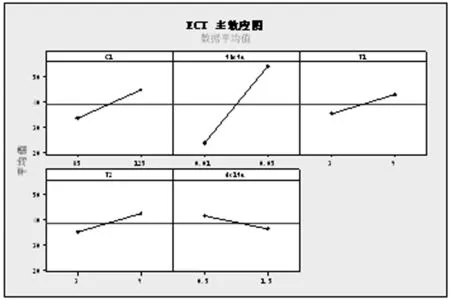
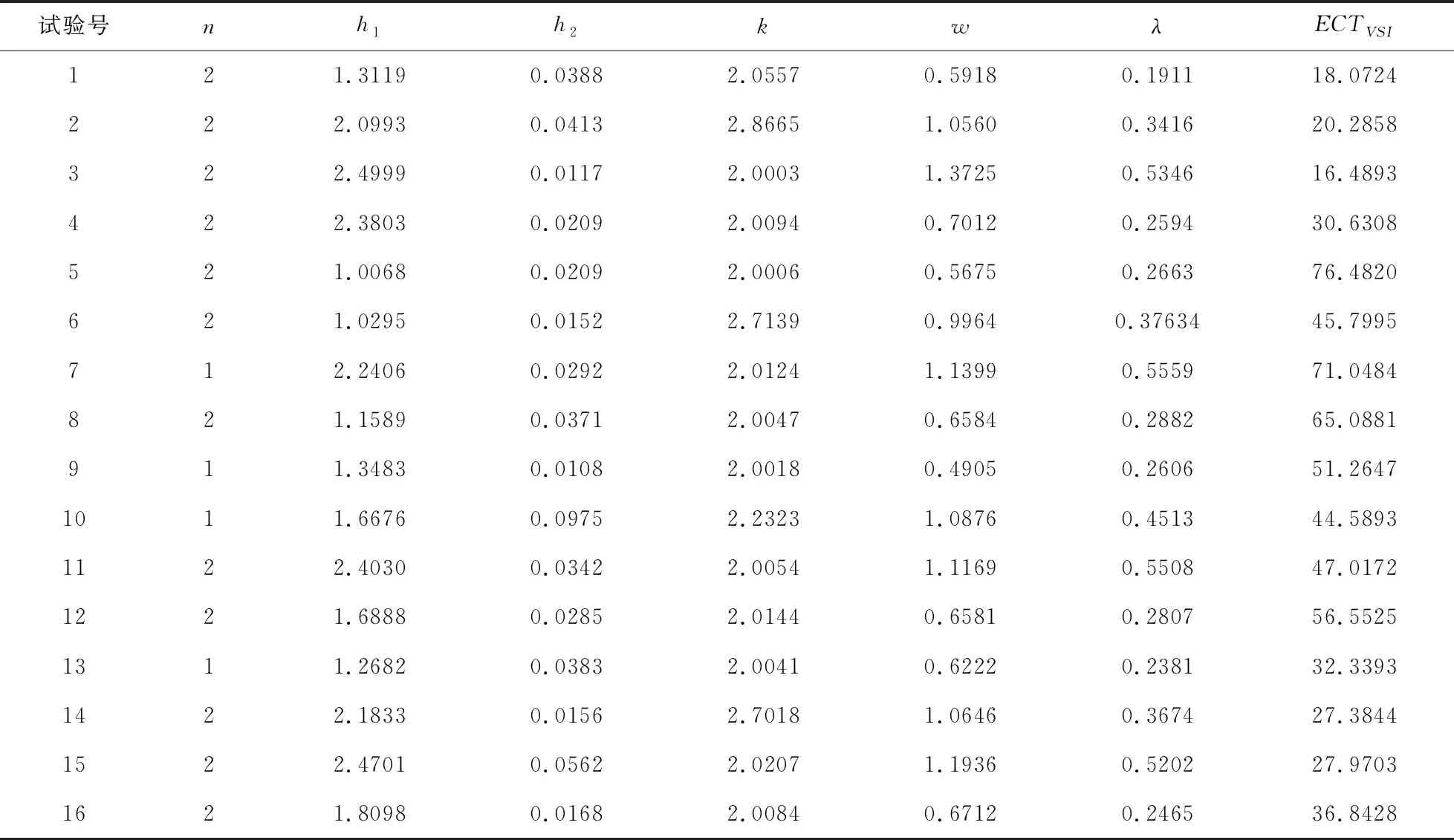
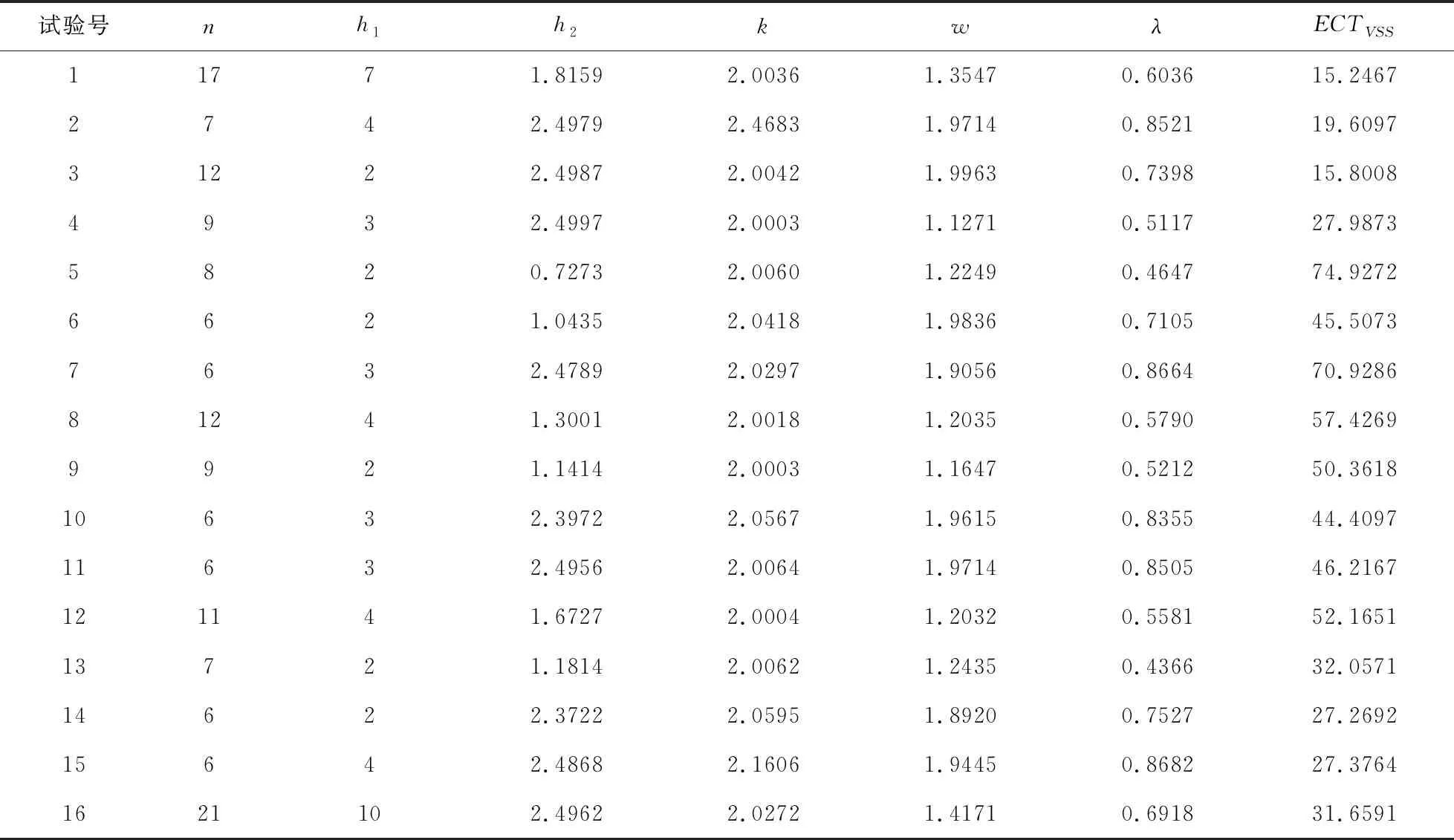
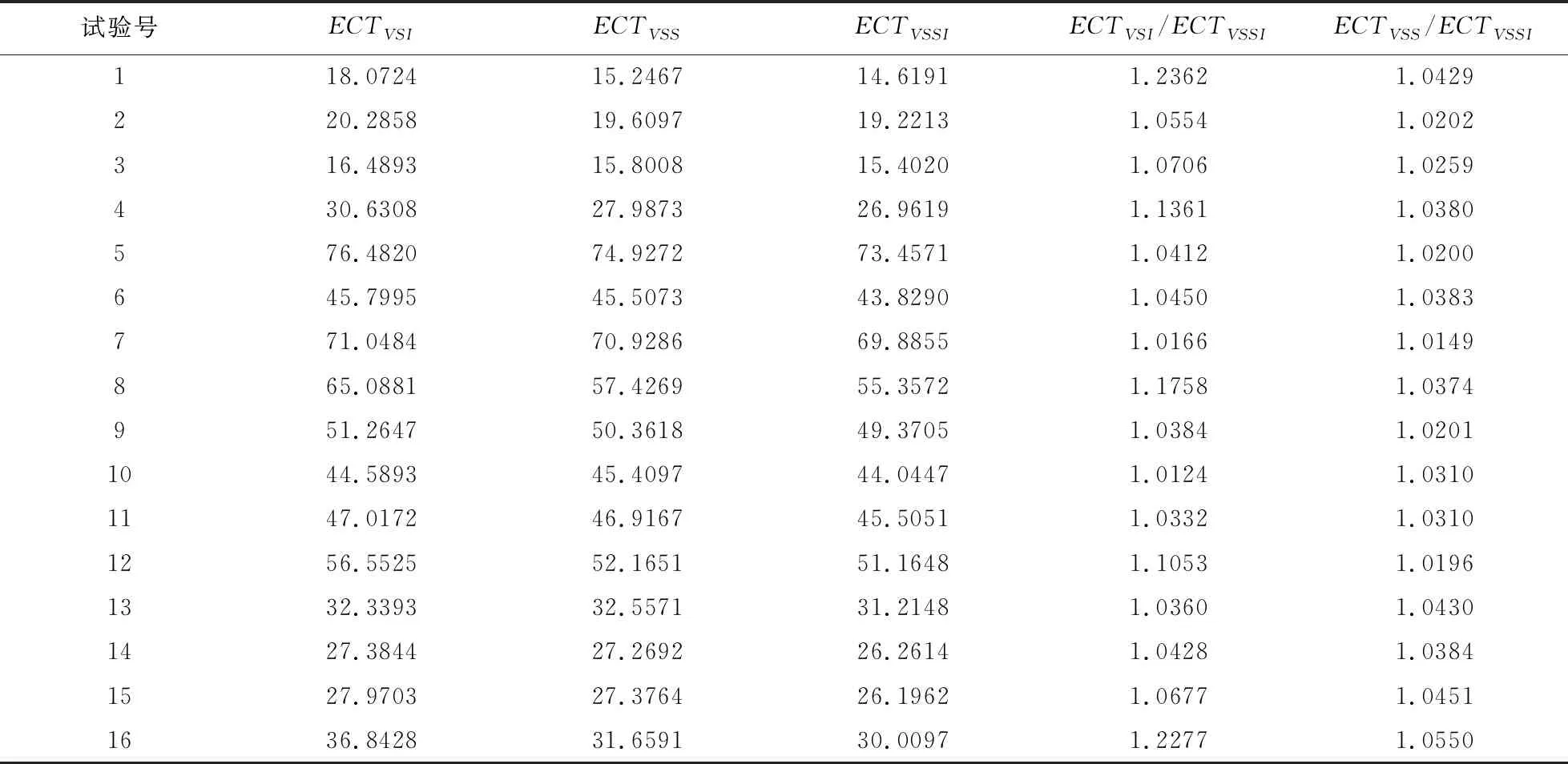
令h1、h2为长抽样区间和短抽样区间,n1和n2为大样本容量和小样本容量。控制图的监控机制为:若当前样本点落在中心域(LWL,UWL)内,则下一次抽样采用大抽样区间h1以及小样本容量n2的抽样办法;若当前样本点落在警戒域(UWL 由于质量特性值的分布未知,需要用一种已知的分布形式去近似它。两参数Burr分布可以近似各种类型的分布,例如Gamma分布,Beta分布等,其分布函数如下: (4) 其中,c和q均为大于1的常数。 针对各种(c,q),Burr将其对应的偏度系数、峰度系数以及均值、标准差列表给出。对于具有相同偏度系数和峰度系数的随机变量X和Burr变量Y可以相互转换,根据观测值的偏度系数和峰度系数,通过列表找到相应的c和q值,从而确定对应的Burr分布函数。观测值和Burr变量之间的转换公式为: (5) (6) (7) 为了对VSSI非正态EWMA控制图进行经济设计,提出以下模型假设:(1)假设过程开始处于受控状态(μ=μ0),经过一段时间以后,过程失控(μ=μ0+δσ,σ保持不变)。(2)受控时长服从均值为1/θ的指数分布。(3)异常原因发生后,在找出并纠正异常原因之前的一段时间,过程一直处于失控状态。(4)在每个抽样间隔内,异常原因发生的次数最多为1,并且在抽样过程中,异常原因不发生。经济模型相关参数定义如表1所述。 Lorenzen & Vance经济模型所考虑的费用成本期望值包括:过程受控时的费用成本、过程失控时的费用成本、抽样和理解结果的费用、错误警报造成的费用、找到特殊原因和恢复过程的费用。由于VSSI 非正态EWMA控制图的抽样区间和样本容量不固定,修改Lorenzen & Vance经济模型中的抽样区间为平均抽样区间,样本容量为平均样本容量,得到VSSI非正态EWMA控制图的费用成本函数ECT: (8) 表1 相关参数描述 运用马尔科夫链的方法得到ATS0、ATS1、ANSS0、ANOS的计算公式如下: R=[rij](2v+1)×(2v+1)=(I-U)-1 (9) 其中Uij=F(B)-F(A)。 (10) 通过前面的讨论可知:VSSI非正态EWMA控制图的经济设计即寻找使目标函数ECT最小时对应的最优参数组合(n1,n2,h1,h2,k,w,λ)。 在炼钢过程中,需要对某种化学成分进行控制,且已知它不服从正态分布。根据收集的数据可知单个观测值的偏斜度和峰度分别为-0.519和3.462。过程受控时μ=μ0=1.5,σ=σ0=1。过程失控时标准差保持不变,μ=μ0+δσ。由于分布未知,可以用c=10和q=10的Burr分布来近似,并采用VSSI非正态EWMA控制图对其进行监控。在其经济模型中,费用参数和模型参数值如下:C0=9,C1=90,θ=0.01,a1=0.6,a4=0.2,E=0.06hr,a2=20,a1=40,γ1=1,γ2=1,T0=0.6hr,T1=2.5hr,T2=2.5hr,δ=1.5。 在matlab(version 7.0)环境下利用遗传算法工具箱进行求解。解向量为(n1,n2,h1,h2,k,w,λ),其中n1、n2为整数,h1、h2、k、w和λ为连续值。求解的过程如下: (1)生成初始种群。随机选取20组作为初始解,各个参数的限制范围如下: 1 (2)选择。分别计算20个初始解的适应度值,本例中适应度值即为目标函数的倒数。适应度好的染色体有较大概率作为幸存者,组成下一代。 (3)交叉。设置交叉率为0.8,交叉办法如下:D1=0.8R+0.2M,D2=0.2R+0.8M。D1为第一个新的染色体,D2为第二个新的染色体,R、M为父辈、母辈染色体,经过20对上一辈染色体随机结合,会产生40个子代。总人口数增加至60。 (4)变异。设置变异率为0.1,则60个解能随机选择6个染色体(60*0.1=6)来实现变异。 (5)重复循环步骤(2)到(5),设置最大遗传代数为100代。运行到100代时算法停止。得到最优参数值:n1=8,n2=3,h1=1.3232,h2=0.0118,k=2.4065,w=1.0526,λ=0.9516,ECT=15.0034。 为了研究模型参数(C0,C1,θ,a3,a4,E,a2,a1,T1,T2,δ)对控制图设计参数(n1,n2,h1,h2,k,w,λ)以及ECT的影响,采用正交试验设计以及回归分析对经济模型进行分析。令控制图设计参数为响应变量,模型参数为自变量。表2记录自变量(模型参数)的两种水平,其余参数固定如下:γ1=1,γ2=1,T0=1,且收集的数据可用c=10和q=10的Burr分布近似。表3(1)记录16次正交试验的方案,表3(2)记录正交试验的结果。 表2 十一个费用参数的两水平 表3(1) 根据L16(215)安排的十六次试验 表3(2) 十六次试验结果 为了研究模型参数对控制图设计参数的影响关系,运用SPSS软件对每一个因变量(设计参数或费用成本函数)进行回归分析。令检验水平α=0.05,得到模型参数对控制图设计参数和费用成本函数的影响关系如下: (1)模型参数对大样本容量n1的取值影响不显著。 (2)小样本容量n2的取值随着抽样和检测的固定成本a3的增大而增大;随着一次抽取样本和绘制控制图的平均时间E以及过程波动δ的增大而减小。 (3)长抽样区间h1的取值随着受控时的平均成本C0、抽样和检测的固定成本a3、消除特殊原因的平均时间T2以及过程波动δ的增大而增大;随着失控时的平均成本C1、产生特殊原因的频率θ、一次抽取样本和绘制控制图的平均时间E以及查找和消除特殊原因的成本a2的增大而减小。 (4)模型参数对小抽样区间h2的取值影响不显著。 (5)产生特殊原因的频率θ、抽样和检测的固定成本a3越大,控制限系数k越小;错误警报造成的平均成本a1、过程波动δ越大,k越大。 (6)警戒限系数w的取值随着一次抽取样本和绘制控制图的平均时间E、产生特殊原因的频率θ的增大而减小;随着抽样和检测的固定成本a3、过程波动δ的增大而增大。 (7)平滑系数λ的取值随着抽样和检测的固定成本a3、过程波动δ的增大而增大;随着一次抽取样本和绘制控制图的平均时间E的增大而减小。 (8)产生特殊原因的频率θ、发现特殊原因的平均时间T1、失控时的平均成本C1以及消除特殊原因的平均时间T2越大,费用成本函数ECT越大;过程波动δ越大,ECT越小。 为了能直观的显示出模型参数对模型参数以及费用函数的影响关系,运用Minitab软件的到的主效应分析图如图1~6所示。 本节分析VSSI 非正态EWMA控制图与VSS非正态EWMA控制图、VSI非正态EWMA控制图的经济设计进行比较,验证所提出的VSSI非正态EWMA控制图经济模型的优越性。VSSI非正态EWMA控制图的费用成本函数ECT(公式(8))中平均样本容量λ退化成样本容量n,即为VSI非正态EWMA控制图的费用成本函数ECTVSI;VSSI非正态EWMA控制图的费用成本函数ECT(公式(8))中平均抽样区间h0退化成抽样区间h,即为VSS非正态EWMA控制图的费用成本函数ECTVSS。 (1)在相同的模型参数组合前提下,分别对VSI、VSS非正态EWMA控制图的费用成本函数运行遗传算法工具箱,得到参数和费用成本函数最优值,结果见表4和表5。 将表4~5得到的ECTVSI、ECTVSS与表3(2)得到的ECTVSSI分别记录在表6, 并同时计算ECTVSI/ECTVSSI和ECTVSS/ECTVSSI,可以看出在每次试验下,ECTVSI/ECTVSSI和ECTVSS/ECTVSSI的值均大于1,说明ECTVSI和ECTVSS的值均大于ECTVSSI的值。即在相同参数设置下,所建立的VSSI非正态EWMA控制图的经济模型均优于VSI非正态EWMA控制图与VSS非正态控制图,具有较小的费用成本。因此,所设计的VSSI非正态EWMA控制图经济模型较VSI、VSS非正态EWMA控制图的经济模型具有优越性。 (2)实例分析:对数据案例4的实际例子进行分析,分别运用VSI非正态EWMA控制图、VSS非正态EWMA控制图、VSSI非正态EWMA控制图对该炼钢过程进行监控,对这三种控制图分别进行经济设计,得到的控制图最优参数和费用成本函数的结果见表7。 由表7可知,VSSI非正态EWMA控制图的费用成本函数为15.0034,均小于VSI和VSS非正态EWMA控制图的费用成本函数。因此,在对炼钢过程进行监控时,本文设计VSSI 非正态EWMA 控制图经济模型均优于VSI、VSS非正态EWMA控制图。 图1 小样本容量n2主效应图 图2 长抽样区间h1主效应 图3 控线限系数k主效应图 图4 警戒限系数w主效应图 图5 平滑系数λ主效应图 图6 费用成本函数ECT主效应图 表4 VSI非正态EWMA控制图十六次试验结果 表5 VSS非正态EWMA控制图十六次试验结果 表6 最优性分析结果 表7 实例分析结果 针对过程数据不服从正态分布的情况,研究VSSI EWMA控制图的经济设计问题。首先对非正态EWMA控制图进行抽样区间和样本容量变化设计;其次建立VSSI EWMA控制图的经济设计模型。通过使费用成本函数ECT最小确定控制图的设计参数(n1,n2,h1,h2,k,w,λ)的值,并运用遗传算法进行求解。然后运用正交试验设计对经济模型进行灵敏度分析,得出费用成本函数ECT与失控时单位时间内的成本C1、产生特殊原因的频率θ、发现特殊原因的平均时间T1以及消除特殊原因的平均时间T2呈正相关,与过程波动δ呈负相关。最后通过最优性分析得出所建立的VSSI非正态EWMA控制图经济模型优于VSI、VSS非正态EWMA控制图的经济模型,具有较小费用成本函数。
2 经济模型的建立
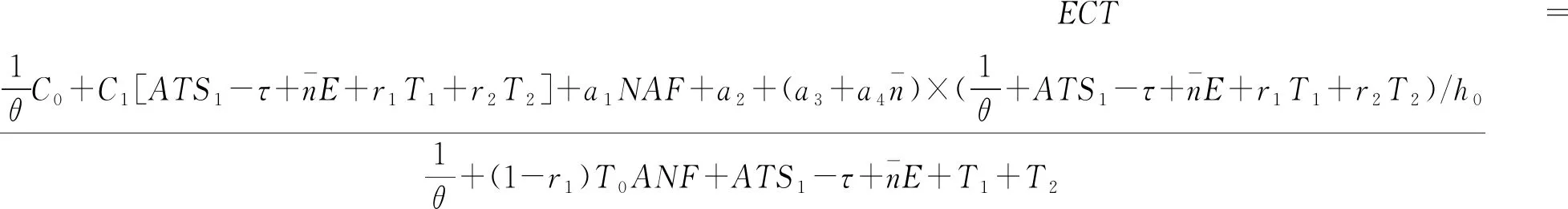

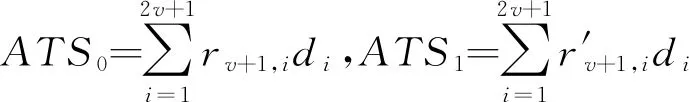
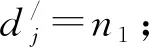
U=[uij](2v+1)×(2v+1)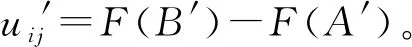
3 算例
4 灵敏度分析

5 最优性分析

6 结论
