基于可靠性弹性指标的系统弹性度量方法
2022-03-15兑红炎陈栓栓陈立伟刘玉敏
兑红炎, 陈栓栓, 马 婧, 陈立伟, 刘玉敏
(1.郑州大学 管理工程学院,河南 郑州 450001; 2.郑州大学 教育学院,河南 郑州 450001; 3.郑州大学 电气工程学院,河南 郑州 450001; 4.郑州大学 商学院,河南 郑州 450001)
0 引言
随着复杂系统在现实生产生活中广泛的应用,对于复杂系统可靠性的研究也不断深入。针对系统可靠性,张权和崔利荣等[1,2]提出了可修系统的可靠性分析,并将其应用于电网系统中,提出了可修系统可靠性的马尔科夫求解方法。基于系统可靠性,兑红炎等[3]分析了部件状态转移对系统失效的影响关系。刘宝亮和崔利荣等[4]将系统运行水平相同的状态归为一类,整个状态空间被划分为多个运行水平,建立了对应的可修模型并进行可靠性分析。兑红炎等[5]针对系统多态性,基于系统可靠性进行部件失效及维修成本分析。
而作为影响系统可靠性的一种重要的恢复能力,对弹性度量的研究和探索从未间断过。潘星等[6]提出了一种基于弹性的体系结构评价方法,对体系的组件或系统进行重要度分析。刘健等[7]针对城市供水系统受外界威胁导致供应能力波动的问题,建立了以优化供水系统弹性为目标的两阶段应对策略模型。欧阳敏等[8]从弹性视角出发,从四个方面进行了研究:地震灾害情形模拟、电网元件脆弱性建模、电网功能变化过程仿真、电网抗震性能评估与改进。兑红炎等[9]分析了组件综合重要度对系统可靠性的影响机理,识别对系统可靠性变化影响最大的组件,综合重要度评估了单位时间内系统可靠性的变化。贾旭杰等[10]利用系统建立数学模型,对该系统的危险失效和安全失效进行定义和算法求解,探索两种失效模式下的系统性能。同时定义了危险、安全失效概率指数,精确计算系统失效时每种失效发生的可能性。
在交通网络的弹性研究方面,王昕等[11]针对存在异质用户的弹性需求交通系统,当用户时间价值呈离散分布时,给出了系统时间最优和系统费用最优的双准则优化模型及其帕累托的有效前沿。证明了存在正的匿名路段收费方案。张敖木翰[12]等研究了突发事故下交通拥堵的控制策略,研究了突发事故下临时性的车辆禁行设计与可变信息板选址组合优化问题。马寿峰[13]等从风险角度提出了一种交通系统可靠性分析方法, 通过高斯核估计,给出了基于历史数据的路段出行时间分布函数的估计与计算方法,从而得到该路段的基于风险的交通可靠性。李兆隆等[14]提出一种基于弹复性的交通系统应急恢复阶段策略优化模型,结合并行机调度问题算法和用户均衡配流问题算法,设计了一种特殊的交互式双层算法。
从以上的文献综述可以看出,对系统弹性的研究本质上是在系统失效后对系统恢复能力和稳定性的研究。一般来说,级联失效是指网络中一个或少数几个节点或边的失效会通过节点之间的耦合关系引发其他节点也发生失效,进而产生级联效应,最终导致相当一部分节点甚至整个网络的崩溃。在分析弹性问题时,考虑了网络中不同节点失效时,剩余节点的弹性以及边的弹性,发生级联失效后整体网络的弹性也会受到影响。本文通过找到系统中的节点和边内在的关联进而找到影响系统稳定性的关键因素,并较为准确地评估某一种特定系统的稳定性能,进而对现有的系统进行适当的调整和改进,以使其具有更加稳定的拓扑结构和性能表现。此外,在构建新的系统时预先做出较为合理的节点和边布局,使得其在最初状态下便具备了良好的拓扑结构,进而减少日后系统维护成本和次数。
1 可靠性节点弹性指标
节点的弹性是节点在发生故障后的恢复能力。本节将从节点之间的相对性与绝对性出发,分别给出节点相对实时负荷量和相对实时负荷转移速率、绝对实时负荷量与绝对实时负荷转移速率等指标,通过这几个指标的结合最终给出整体系统弹性度量。一般系统中任一节点的负荷流动状态由三个方面决定,分别是节点自身原有负荷随时间的变化特征、上游节点的外来负荷随时间的变化特征以及下游节点的外来负荷随时间的变化特征。而节点的绝对实时负荷量指不考虑节点所处的上下游拓扑结构,仅考虑自身的负荷量随时间的变化特征的情形,而绝对负荷转移速率可以通过绝对实时负荷量求导得出,其含义是指节点在单位时间内转移的负荷量。节点的绝对实时负荷量Qi(t)表示为
(1)
(2)
节点的相对实时负荷量是指不考虑该节点自身原有负荷的转移特征,单位时间内上游节点每转移单位负荷量,下游节点转移的负荷量大小。以任一节点i为研究对象,其上游节点为pq,下游节点为rq,则节点i的相对实时负荷量表示为。
(3)



(4)
对于节点的相对实时负荷转移速率的变化率,它反映了节点的相对实时负荷转移速率的变化程度的快慢,对相对实时负荷转移速率求导后得到。在某一节点失效引发的级联失效过程中,不同节点的相对负荷转移速率随时间而不断变化,若转移速率变化地较慢,则表明在一定的时间内,该节点内相对实时负荷转移速率的变化量较小,进而反映该节点在保持自身稳定性的基础上可承受的传递速率的范围较小;反之,若转移速率变化地较快,则表明该节点可承受的传递速率的范围较大。因此,当某一节点q失效时,节点i的相对实时负荷转移速率变化率可以用RQi″(Ti)表示。

(5)
由式(5)可以看出,相对负荷转移速率的变化率是随时间变化不断变化的,且当某一节点对确定时,转移速率的变化率仅和初始失效的节点以及级联失效耗用的总时间相关。

(6)
2 可靠性边弹性指标
每一条边总是被多个路径所经过,不同的路径由不同的边数目构成,而在不同的路径中,同一段边在每条路径中所处的序列数不尽相同,我们将该段边所处的某一条路径的序列数称为边在该条路径上的层级值。层级值越高,说明该边位于该条路径中的下游,反之则更加靠近上游。以此类推,系统也可看作是由不同层级的边构成的节点组合。若要计算某条边在系统中所处的位置和层级值,需要对同一条边在不同条路径中的层级值取均值处理,并将该均值等效为该条边在系统中的值,将这种边分层的特征称为边的层级性。
(7)
式(7)中ERj表示边j在系统中的层级值大小,nj表示该条边一共被经过的路径总数。Hλ表示第λ条路径中所有的边数目,而hλ表示在第λ条路径中该条边j所处的序列数。
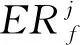
(8)
3 基于可靠性弹性指标的系统弹性
本节将从节点弹性与边弹性入手,综合节点的弹性和边的弹性给出系统弹性度量。节点的弹性和边的弹性共同影响着系统的弹性,利用加权思想综合衡量节点和边的共同影响。

(9)
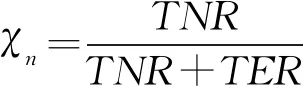
4 算例分析
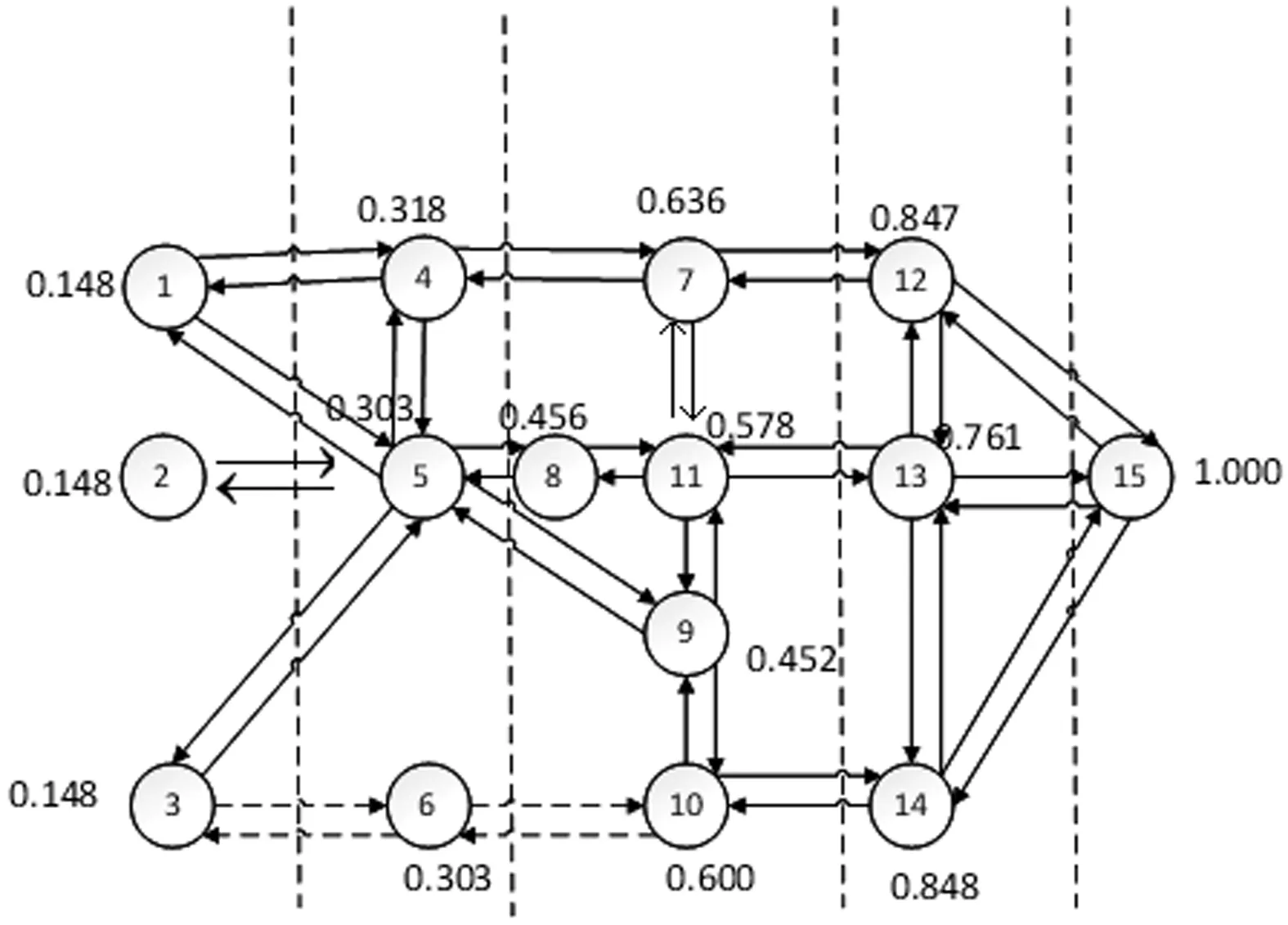
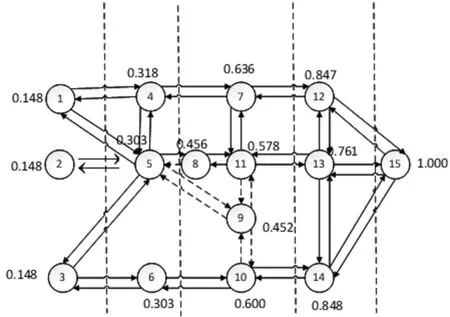
本节给定一个具有15个节点,22条边的分层交通系统算例图,基于该交通系统验证上述所提系统弹性度量方法,如图1所示。

图1 交通系统图
在图1中,节点的数据表示层级值,是对系统负荷传播的梯度性质的形象描述。层级值的范围是(0,1],层级值越接近0,则说明该节点处于系统上游,层级值越接近1,则说明该节点处于系统下游的位置。以图1中节点1为例,一共有12条线路经过节点1,以其中任意一条线路1-4-7-12-15为例,该条线路一共由5个节点组成,而节点1所处的序号是第1个。因此在该条线路上,节点1的层级数为1/5,以此类推可以得出其他11条剩余线路中节点1的各自层级数,这12个数求层级值得出对于节点1的层级值为
从图1可以看出,处于同一层级的节点成员的层级值相近,这说明该类节点成员在遍历所有系统链路的情形下处于同一层级范围内,且同一类节点成员的初始负荷量和负荷承载能力是相近的。
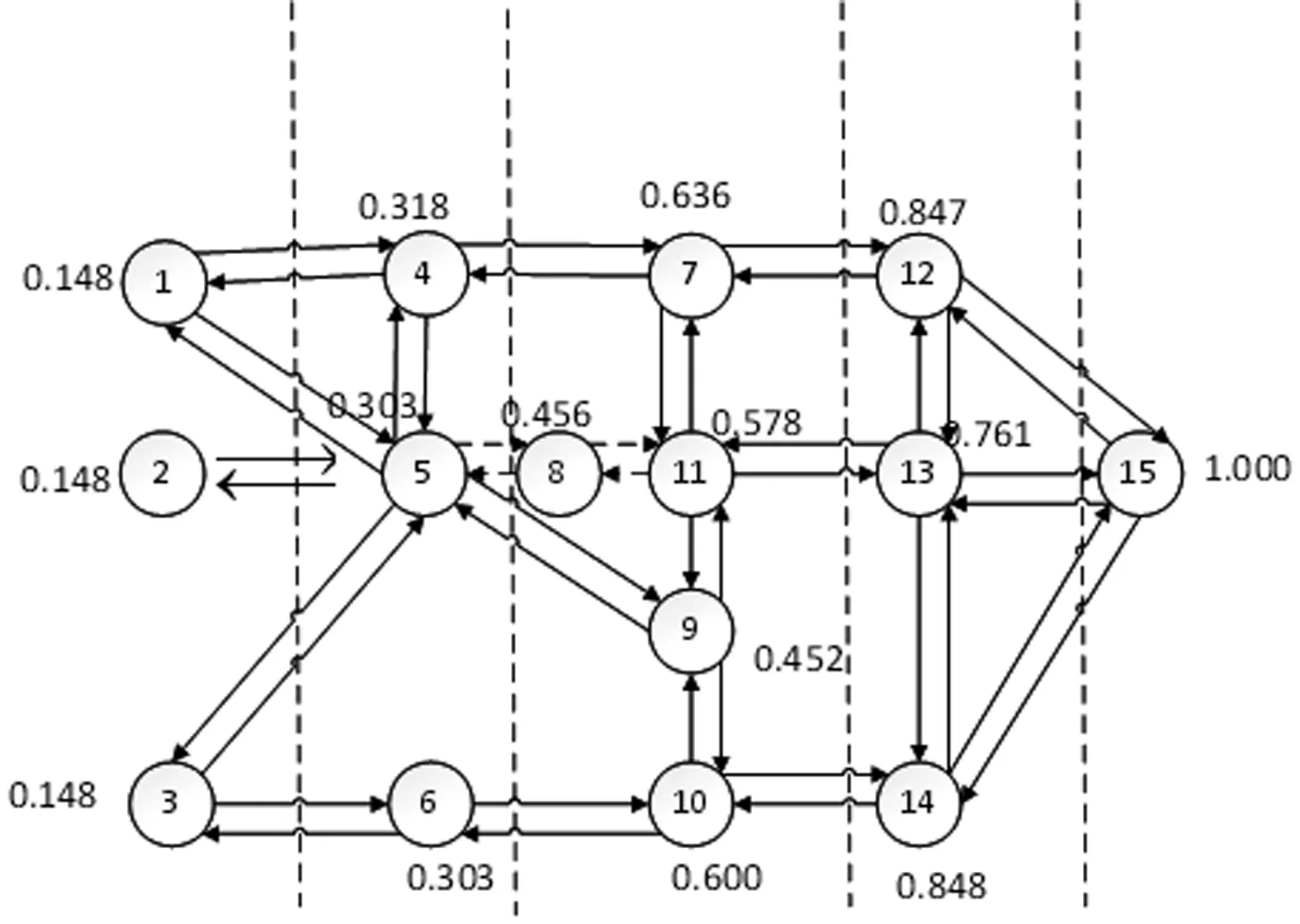
考虑不同初始的失效节点为不同的级联失效情形,某个节点失效时会引起与其相连的边失效,最终可以得出每一种节点作为初始失效点情形下的交通网失效过程图,如图2所示。

a.初始失效节点为节点1

b.初始失效节点为节点2

c.初始失效节点为节点3

d.初始失效节点为节点4
f.初始失效节点为节点6

g.初始失效节点为节点7
h.初始失效节点为节点8
i.初始失效节点为节点9

j.初始失效节点为节点10

k.初始失效节点为节点11

l.初始失效节点为节点12

m.初始失效节点为节点13

n.初始失效节点为节点14
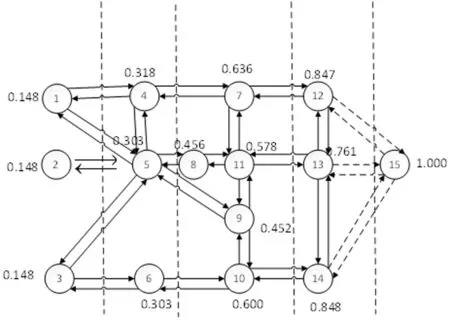
o.初始失效节点为节点15
在图2中,虚线部分表示由于节点失效导致的边失效,组图忽略所有失效节点以及虚线的边,即为各自情形的级联失效发生后新的系统拓扑图。从图2可知,若从节点失效和边失效的数目衡量级联失效规模的大小,则节点5失效带来的影响最大,节点11和节点13作为初始失效点的影响次之,而靠近系统两侧的节点作为初始失效点的影响较小,仅表现为其自身的失效,如节点1,节点2和节点3。
针对交通网,边数量和节点数量对弹性都会产生影响,边弹性和点弹性的趋势变化如图3所示。

a.边弹性变化

b.点弹性变化
从图3可知,边在系统中的弹性分布呈现出“双峰”状,即依次从上游到下游看,会出现两次边弹性值“先上升后下降”的趋势变化过程;而节点在系统中的弹性分布呈现出“单峰”状,即依次从上游到下游看,仅出现一次点弹性值“先上升后下降”的趋势变化过程,表明失效节点仅对其附近的连边产生较大程度的影响,其影响程度在节点4的位置达到最大,然后影响程度逐渐下降,直到趋于平缓。节点对系统的稳定性的影响要大于边对系统的稳定性的影响,因此,对整个系统中较为重要的节点进行重点维护可以提高系统的可靠性与弹性,通常来说,节点承载负荷能力越大,说明该节点在整个系统的位置越重要,但是当承载负荷的节点受到外部攻击或其他事故导致该节点失效时,对整个系统会产生很大的影响,越重要的节点应该更要加强对它的不定期维护与检查。
针对算例系统的15个节点,22条边,结合公式(9)的系统弹性计算方法,最后经过计算得出系统的整体弹性程度为62.24%。当弹性程度是 100%时,认为该系统是具有完全弹性的,可以抵抗任何规模和任何类型的干扰。当弹性程度为0%时,认为该系统是完全不具备弹性的,任何小的干扰都有可能造成系统的大规模级联失效。由此可见,弹性程度为62.24%的系统是缺乏弹性的,弹性程度属于中等,这可能与单源头节点和单汇聚节点相关,由于最上游节点和最下游节点的唯一性,系统在对抗外来干扰时的能力会被局限。
5 结论
本文从节点和边的角度分析了系统弹性的度量,节点和边之间存在着必然的联系,节点的弹性是在不考虑自身的负荷流动情况下对外来负荷进行的描述,单个节点的发生故障会导致至少一条边发生故障,而单个边的故障不一定会导致其连接的节点的故障,因此相较于边的弹性,节点的弹性对系统稳定性的影响更大。另外,边发生故障对系统的破坏程度要小于节点发生故障,且一般而言边故障一般伴随着节点的故障,因此边弹性对系统稳定性的影响较小。对于分层交通系统,若出发点较多,分层较多,出发点与目的地之间的各条路线多。当路况复杂时,交通系统的整体弹性就会很低,此时,若在某条街道上发生交通事故,可能会造成整个交通系统的瘫痪。
