鼓泡流化床内高灰煤气化过程的颗粒尺度特性研究*
2022-03-14杨世亮胡建杭
梁 锦 杨世亮 胡建杭
(昆明理工大学省部共建复杂有色金属资源清洁利用国家重点实验室,650093 昆明)
0 引 言
在富煤、贫油、少气的资源分布特征下,我国以煤炭为主的能源结构在短期内很难被完全取代,因此实现煤炭高效的清洁利用、促进行业节能减排的需求日益迫切[1-4]。煤气化作为一种现代化节能技术是实现煤炭高效利用的途径之一,近年来备受瞩目[2,4]。煤气化是通过煤与气化剂反应生成可燃合成气(氢气、一氧化碳和甲烷)的过程,具有转化效率高和低排放的优点。主流的煤气化技术包括固定床气化、流化床气化以及气流床气化。流化床气化主要应用于鼓泡流化床气化炉(BFBG)和循环流化床气化炉(CFBG)两大类,其中鼓泡流化床因操作简单、固体燃料适应性广、气固相传热性能良好、床温负荷调节可控等优点而被广泛采用[5]。
由于气-固流动受高温高压条件的限制,实验研究无法测得气化炉内真实情况,缺乏对固体颗粒热化学特性的探索[2,6]。随着计算机技术的不断发展进步,越来越多的研究人员通过计算流体力学数值模拟方法对流化床内稠密气固两相流系统进行研究[7]。该方法可以准确获得反应器的流速分布特征、气体组成和温度分布等流场参数[8],且计算成本低,周期短,成为近年来热门的研究方式。根据固体颗粒的不同跟踪方式,数值方法通常分为双流体模型(two-fluid model,TFM)、计算流体力学耦合离散元模型(computational fluid dynamics-discrete element method,CFD-DEM)以及多相流体网格质点模型(multiphase particle-in-cell,MP-PIC)。其中,TFM模型在欧拉框架下将气相和固相看作连续介质,计算速度快,但精度小,难以追踪单个颗粒尺寸信息。基于欧拉-拉格朗日框架中的CFD-DEM模型和MP-PIC模型是计算气固两相流动更好的选择,前者可以获得精确颗粒尺度信息,准确模拟单个颗粒间碰撞作用力,但计算单个粒子间碰撞消耗资源巨大,仅适用于小规模设备;后者采用固体法向应力模型简化颗粒碰撞问题,既可以有效跟踪固体粒子的轨迹,又能够计算大规模的气固流动。MP-PIC模型由ANDREWS et al[9]在1996年首次提出。目前利用计算机流体力学数值模拟的方法已经成功地用于探索流化床反应器中固体颗粒的气化反应过程[10]。WANG et al[11]基于欧拉模型对煤气化过程建立了气固耦合化学反应的三维数值模型,并将模拟结果与实验结果进行对比以验证欧拉模型的正确性。SNIDER et al[12]对三维流化床煤气化炉内在流态化、热传递和化学反应的相互关系进行了探讨。HU et al[13]对鼓泡床煤气化在不同操作条件下进行研究,结果表明,气化速率和床料粒径影响气化过程中颗粒分布。XIE et al[14]探讨了鼓泡流化床中的煤颗粒在不同操作条件下的颗粒形态、流型形成、气体组成分布和反应速率分布,验证了欧拉-拉格朗日数学模型是研究复杂气固流动和化学反应特性的有效工具。
目前,大多数关于流化床气化过程的数值模拟主要从宏观尺度讨论了不同操作参数和设计参数的影响。然而,对于在鼓泡流化床中煤气化过程固体物质颗粒尺度热化学性质的研究较鲜见[15]。本研究为探究煤颗粒在流化床气化过程中的颗粒尺度热化学性质,考虑了致密颗粒和气体的流动、传质和传热、相间和流体混合物内的均相和非均相化学反应。在设置模型参数后,基于出口气体的摩尔分数与实验数据进行对比,验证了MP-PIC模型的准确性。此外,还探讨了煤颗粒的颗粒尺度热化学性质(即温度、传热系数、速度和停留时间)在鼓泡流化床煤气化过程的影响。
1 数值模型
1.1 气相控制方程
在MP-PIC模型中,气相流体采用欧拉方法,由Navier-Stokes方程进行控制,通过大涡模拟(LES)进行求解,气相的连续性方程和动量方程表示如下:
(1)
(2)
组分方程和能量守恒方程表示如下:
(3)
(4)
1.2 固相控制方程
固相粒子采用拉格朗日方式求解。颗粒相空间分布采用概率分布函数(PDF)来描述,通过追踪计算颗粒的运动获得颗粒的空间分布。颗粒分布函数fs结合t时刻的颗粒位置x、速度us、质量ms及温度Ts来描述颗粒的相运动。PDF传输方程表示如下:
(5)
式中:fD表示局部平衡时的颗粒分布函数。
计算粒子加速度的表示方程如下:
(6)
通过颗粒的概率分布函数(PDF),可以得到颗粒的体积分数分布如下:
(7)
Ds是通过Wen-Yu模型[16]计算气固相间的曳力得出,Wen-Yu阻力模型表达如下:
(8)
(9)
(10)
考虑到粒子动力学采用粒子分布函数,流体相的单位体积受到颗粒作用力为:
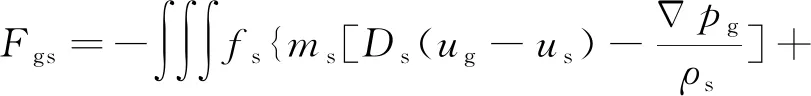
(11)
从颗粒相到流体相的能量交换:
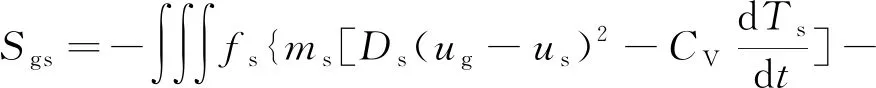
(12)
1.3 化学反应模型
煤颗粒进入反应器后,经过干燥、热解、均相和非均相反应等过程。随着温度的升高,煤颗粒中的水分受热蒸发,挥发分释放;随着温度进一步升高,发生碳的气化反应。相关化学反应式和化学反应速率见表1[14,17]。过程描述如下:
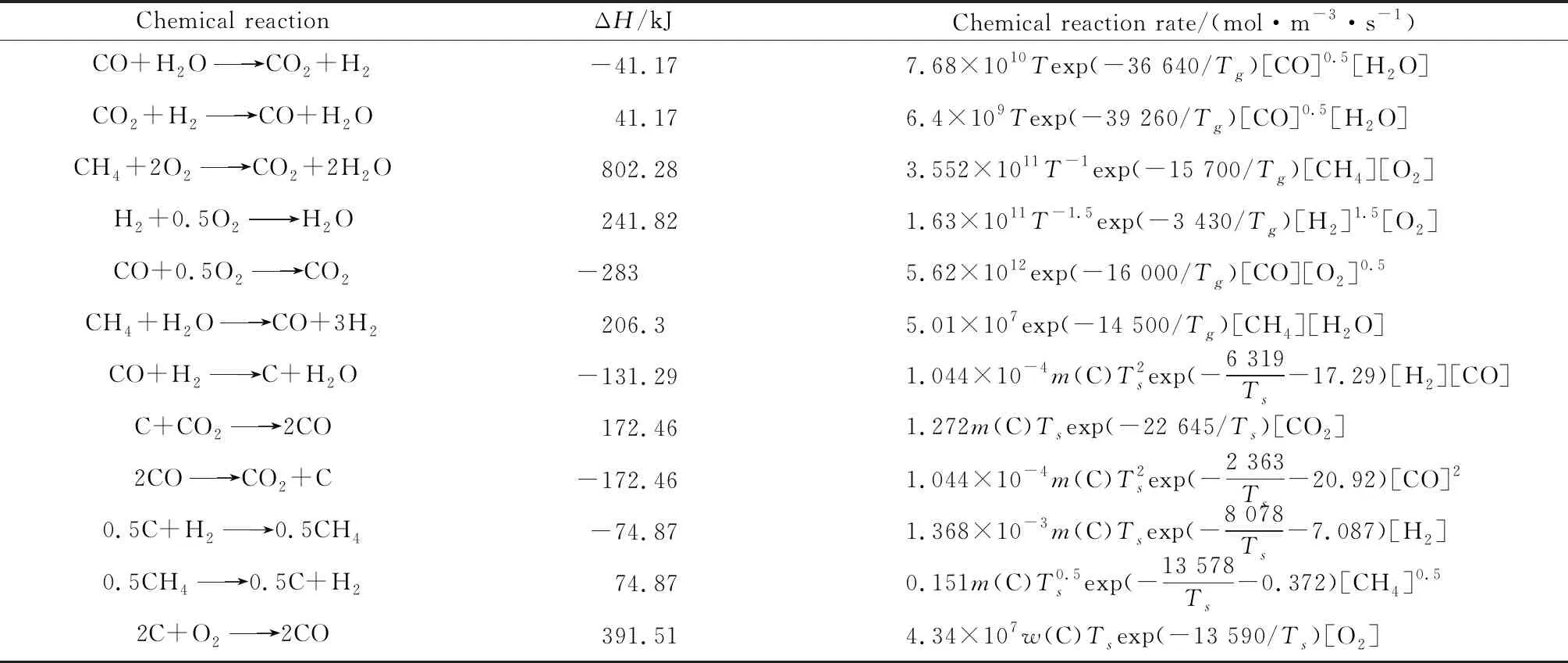
表1 化学反应和化学反应速率

(13)

(14)

(15)
式中:m1=0.201 453;m2=0.134 615;m3=0.017 873;m4=0.272 998。
2 计算模型及参数设置
2.1 计算对象和计算参数设置
本研究的反应器是基于ENGELBRECHT et al[17]实验研究的三维鼓泡流化床气化炉装置(如图1所示)。该反应器为截面为正方形的柱体,分别由下方边长为0.2 m的床段和上方边长为0.4 m的自由空域段组成,两段高度均为2.0 m,反应器总高为4.0 m。初始状态整个反应器内充满氮气,床层温度设置为1 153 K。从气化炉底部通入由氧气、水蒸气和空气组成的常温气化剂,进口流率分别对应为8.9 kg/h,16.5 kg/h及31.2 kg/h。引入煤的进料器在气化炉上方1.3 m处,煤颗粒以32.2 kg/h的进料速率从反应器侧方通入。煤颗粒平均粒径为1.8 mm,密度为1 250 kg/m3,初始温度为300 K。床料采用密度和体积分数分别为2 700 kg/m3和0.45的砂粒,床料粒径范围为0.4 mm~0.85 mm,其填充高度为0.45 m。边界条件采用速度入口和压力出口(其中压力为常压)。基于OpenFOAM开源软件采用MP-PIC方法对三维鼓泡流化床反应器进行数值模拟,计算出的最终网格数量为61 720个,计算颗粒数量为7 684个。设定时间步长为1×10-3s,共模拟30 s。高灰煤的工业分析和元素分析见表2[17]。

表2 高灰煤的工业分析以及元素分析
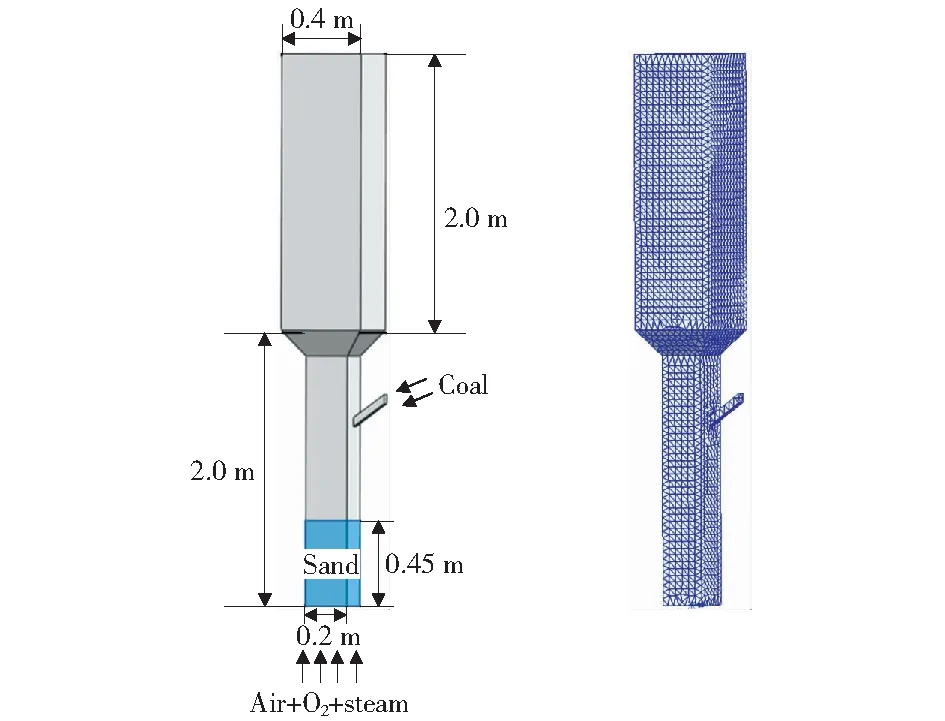
图1 气化炉反应器结构和网格划分
2.2 模型验证
为验证该反应模型,将数值模拟得到的气化炉出口气体的模型结果与实验数据对比,结果如图2所示[17]。由图2可知,模拟结果与实验数据对比结果良好,验证了模型设置的可靠性和合理性。每种气体的摩尔分数的大小趋势与实验数据基本一致,即N2含量最多,其次是H2,CO2和CO,CH4占比最少。CO,CO2,H2气体摩尔分数的偏差可能是由反应器结构模型的简化以及化学反应动力学模型的简化导致[18]。
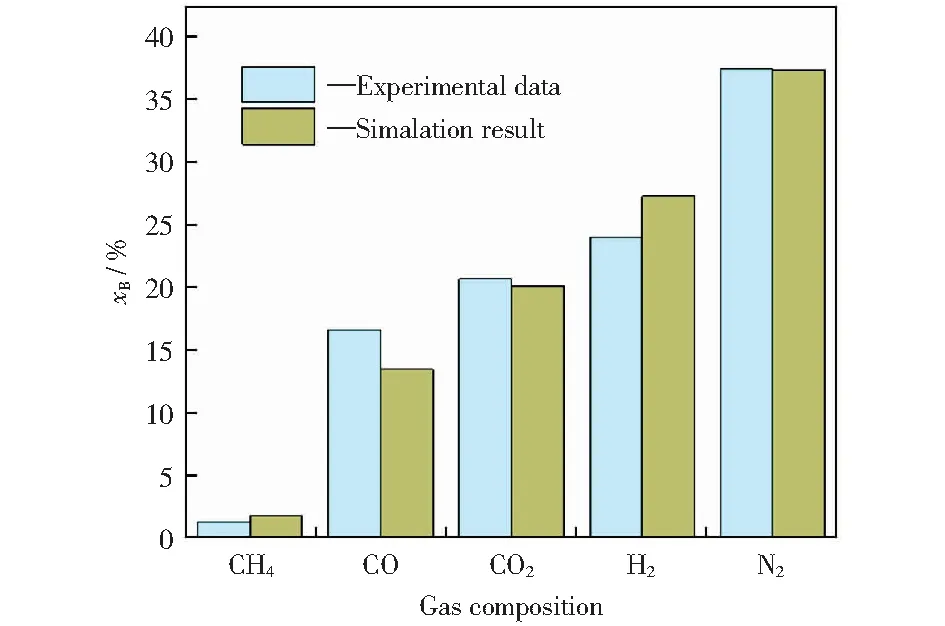
图2 气化炉出口气体组分模拟结果与实验数据的比较
3 结果与讨论
3.1 组分分布
图3所示为在BFBG内y/z中心截面所有煤颗粒中碳、挥发分和灰分质量分数着色的颗粒分布。反应器内存在多种复杂的物理化学反应过程,导致煤颗粒中碳、挥发分和灰分的不均匀分布。由图3a可以看出,在进料器入口处碳的质量分数约为0.35,碳含量在进料器周围最大。碳含量主要集中在进料器附近以及床层附近。由于气泡的生长并聚结,夹带颗粒向上运动,质量较轻的颗粒出现在自由空域区。由于存在与焦炭相关的多种化学反应,反应器大部分区域碳的质量分数均有所下降。颗粒在进入反应器后,挥发分会在极短时间内快速释放,因此可以观察到进料口处挥发分含量最大,在其余区域挥发分含量趋于零(见图3b)。在水分和挥发分迅速释放后残留碳和灰分,碳含量和灰分含量分布趋势相反,由于重量轻,灰渣在反应堆顶部聚集,反应器中绝大部分区域灰分含量高(见图3c)。
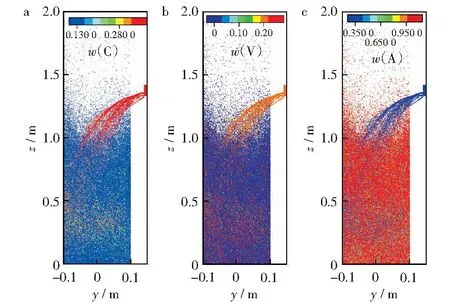
图3 鼓泡流化床煤颗粒中碳和挥发分及灰分的分布
图4所示为BFBG中煤颗粒各组分质量分数随时间的变化曲线。由图4可知,在初始时期,因进料器不断引入煤颗粒,煤颗粒中水分和挥发分的质量分数有所增加。由于反应器内温度比引入的煤颗粒温度高,在煤颗粒被送入反应器之后,发生干燥过程和热解过程,水分快速析出,挥发分释放,因此煤颗粒中二者的质量分数随时间逐渐下降。焦炭与气体发生非均相反应,碳的质量分数持续降低。随着时间的推移,煤颗粒的灰分逐渐累积增加。在反应20 s之后,煤颗粒各组分的质量分数逐渐趋于稳定。反应器中灰分的质量分数最大,其次是煤颗粒中的碳、水分和挥发分的质量分数。
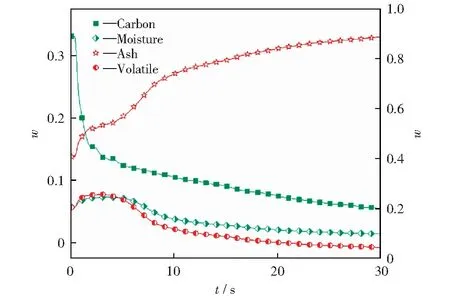
图4 鼓泡流化床中煤颗粒各组分质量分数随时间的变化曲线
3.2 速度分布
图5所示为反应30 s内BFBG中煤颗粒在各个方向上的瞬时速度分布和颗粒着色分布。由图5可以看出,颗粒的运动速度空间分布不均匀。反应器底部产生的气泡和颗粒之间会产生强相互作用,导致颗粒速度在三个方向的分布存在明显差异。在床层中部固体颗粒在三个方向均表现出混乱和不均匀的分布,这是气泡的生长聚结和破裂,固体颗粒的强烈返混行为引起的混沌运动所致。在床层上部的自由空域区,质量较轻的颗粒进入上方,在垂直方向呈现剧烈的运动。由于气化剂从反应器底部垂直方向引入,气相和颗粒以及气泡和颗粒之间发生剧烈的动量交换,导致颗粒的垂直运动速度较大。
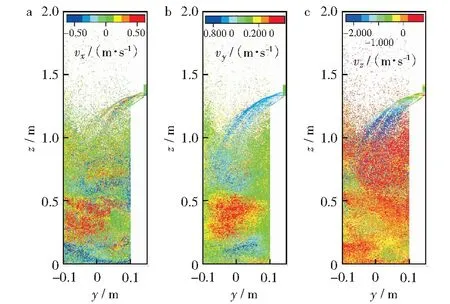
图5 鼓泡流化床中煤颗粒在各个方向的速度分布
图6所示为在BFBG中各个方向上速度随时间变化的分布。由图6可以看出,随着时间的变化,煤颗粒和床料在三个方向上的运动规律基本一致,颗粒速度均在一个区间内波动。其中,煤颗粒参与反应而砂粒未参与反应,但两者速度分布相似,这说明颗粒在气化炉内的运动受化学反应的影响较小[10]。在初始状态,气泡的生长、聚结和破裂引起颗粒强烈的混沌运动,导致煤颗粒与砂粒速度较大。由图6还可以看出,煤颗粒的垂直扩散速度最大,煤颗粒沿y方向的瞬时速度相比于砂粒沿y方向的瞬时速度更大,x方向上两者的水平速度相似,说明气固混合较为剧烈。颗粒在垂直方向的速度明显大于水平方向,因为该方向通入气化剂,加速气泡带动颗粒向上运动。

图6 鼓泡流化床中煤颗粒和砂粒在各个方向的速度随时间的变化
3.3 颗粒温度
图7所示为在BFBG中煤颗粒的温度分布散点图及相应的直方图。由图7a可知,在进料器附近,刚引入的煤颗粒温度不高,和气化炉内高温环境存在较大温差。经过一系列复杂的物理化学反应,焦炭完全氧化释放出大量的热量,导致煤颗粒与周围环境通过传热、对流换热以及热辐射等途径不断进行热交换从而迅速提高了煤的温度。由图7b结合图7a可以看出,约20%的低温颗粒与进料口附近的颗粒温度相对应,约80%的高温颗粒与气化炉内部温度相对应。在焦炭发生氧化反应释放大量热量之后,温度迅速升高,最大温度达到1 160 K左右,约为初始床层温度(1 153 K)。反应器内出现的较大温差也表明了鼓泡流化床中颗粒与周围环境之间良好的传热性能。
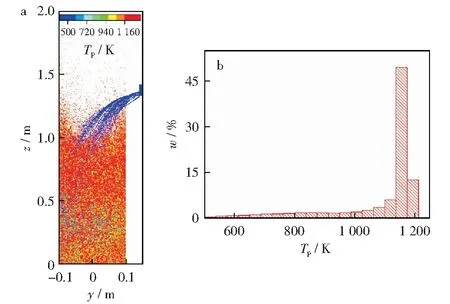
图7 鼓泡流化床中煤颗粒的温度分布
3.4 颗粒传热系数
传热系数是指在稳定传热条件下,单位时间通过单位面积传递的热量,反映了传热过程的强弱。图8所示为鼓泡流化床气化炉中煤颗粒的传热系数的散点图及相应的直方图。由于气相和固相之间强烈的热交换,导致颗粒在气化炉内传热系数分布不均匀。由图8a可以观察到入口周围传热系数较大。这是由于:1) 进料器入口处刚引入的煤颗粒温度与炉内高温环境之间温差较大;2) 反应器底部入口处气化剂温度与气化炉内高温床层温差较大。此外,在自由空域区的剧烈对流传热归因于悬浮的煤颗粒与炉内存在较大温差以及涉及到的化学反应。在床面附近,煤颗粒和床料之间的温差小,因此对流传热很小。由图8b可知,大部分煤颗粒的传热系数在70 W/(m2·K)左右占比最大,约为40%,对应于反应器中心区域,而传热系数超过210 W/(m2·K)的煤颗粒只占一小部分,约为5%,对应于反应器的进料器附近区域。煤颗粒温度逐渐增大,与周围环境的温差越来越小,传热系数逐渐降低。
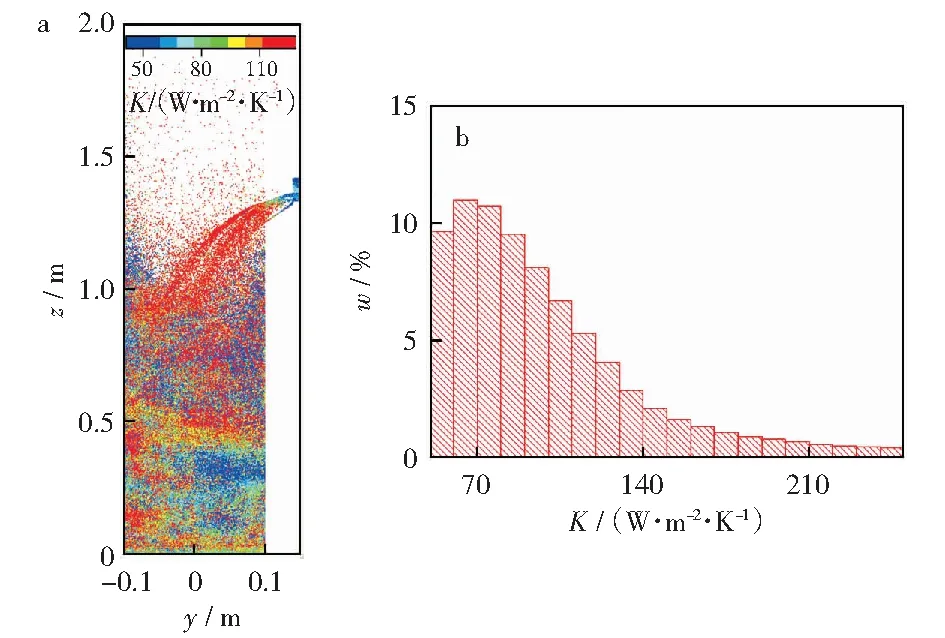
图8 鼓泡流化床中煤的颗粒传热系数
3.5 颗粒停留时间
图9所示为在BFBG中煤颗粒停留时间的散点图和直方图。煤颗粒的停留时间为从引入煤颗粒的时间到离开反应器出口的时间间隔。由图9a可以看出,在进料器口附近的颗粒停留时间较短,而其他区域的颗粒停留时间较长。这是由于在近壁面出现剧烈的返混行为,导致煤颗粒在反应器中的反应时间延长。由图9b可以看出,颗粒在气化器内的停留时间总体呈现均匀分布。
4 结 论
1) 在流化床气化炉中,进料口处煤温度和气化剂温差大、传热系数高,导致煤颗粒的传热系数和温度在整个反应器内分布不均匀。煤颗粒的传热系数在进料器附近达到峰值后逐渐下降,大部分颗粒传热系数集中在70 W/(m2·K)。
2) 与砂粒相比,煤颗粒速度略大,且在垂直方向比水平方向大几倍。气化剂在垂直方向引入导致颗粒在垂直方向运动最剧烈。煤颗粒和砂粒的运动规律相似,其中煤颗粒参与气体反应,砂粒不参与反应,表明颗粒运动趋势受化学反应的影响不大。
3) 颗粒在时间和空间上的分布变化,显著地体现在气固相之间强烈的动量交换和热量交换,导致固体颗粒出现混沌运动,延长煤颗粒停留时间,表明鼓泡流化床的优异混合性能和传热性能。
符 号 说 明
φg—气相体积分数,无量纲
ρg—气相密度,kg/m3
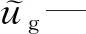
ug—气相速度,m/s
t—时间,s

pg—气相压力,Pa
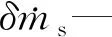
g—重力加速度,m/s2
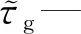
Fgs—气固动量交换源项,N
i—气体种类,无量纲
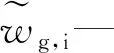

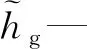
q—气体热通量,W/m2
Sgs—气固热交换,kg/(m2·s2)
Sgw—气壁热交换,kg/(m2·s2)
ΔHrg—化学反应产生的能量,W/m3

Dt—与黏度相关的湍流质量扩散率,无量纲
us—颗粒速度,m/s
τD—颗粒碰撞松弛时间,s
a—颗粒加速度,m/s2
Ds—曳力系数,kg/(m3·s)
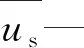
φs—固相体积分数,无量纲
ρs—固相密度,kg/m3
ms—粒子质量,kg
Ts—粒子温度,K
Res—颗粒平均滑移雷诺数,无量纲
ds—颗粒粒径,m
CV—颗粒比热容,J/(kg·K)
CD—单颗粒阻力系数数值模型,无量纲
K—传热系数,W/(m2·K)
Es—固体浓度,无量纲
