小学高年级学生数学元认知水平常模的建立及其应用案例<br/>——以天津市为例

小学高年级学生数学元认知水平常模的建立及其应用案例
——以天津市为例

2022-03-12王光明周鹏冉

天津师范大学学报（基础教育版） 2022年2期

王光明，陈霞，周鹏冉

元认知是关于认知的认知，是反映或调节认知活动的任一方面的知识或者认知活动[1]，是认知活动的核心[2]。数学元认知是对自身数学认知的认知，本质是对数学认知活动的自我认识、自我监控和自我调节[3]，是影响数学学习的重要因素[4]。随着国内外对数学元认知研究的不断深化，涌现了一系列颇具影响力的数学元认知测评工具[5][6][7][8]，采用相关测评工具进行的应用研究也不断涌现[9][10][11]。然而，由于缺乏评价的参照系，无法在同一衡量标准下对测量结果进行比较分析，从而降低了测评工具的使用价值。

2020年10月，中共中央、国务院印发《深化新时代教育评价改革总体方案》，要求“促进学生全面发展的评价办法更加多元”[12]。天津师范大学王光明团队基于国内外相关研究，针对小学高年级、初中、高中等基础教育不同学段的数学学习者，开发了一系列数学元认知水平调查问卷[13][14][15]。其中《小学生数学元认知水平调查问卷》信效度良好，是测量小学生数学元认知水平的可信工具。但是，目前尚缺少将此量表工具应用于测评实践的常模研究。因此，构建小学数学元认知水平常模并开展案例研究，既有助于贯彻落实新时代教育评价改革任务，又有助于全面推广小学数学元认知水平测评问卷，为精准测评小学生数学元认知水平提供新的视角和方法。

本研究拟解决以下研究问题：（1）如何构建天津小学高年级学生数学元认知水平常模。（2）如何利用所建常模划分小学高年级学生数学元认知水平的不同等级并归纳其具体特征。（3）如何应用所构建常模进行案例分析。

一、研究方法

（一）测评工具

以王光明等编制的《小学生数学元认知水平调查问卷》为测量工具。问卷包含数学元认知的三个主维度（数学元认知知识、数学元认知体验、数学元认知监控），以及十个子维度（个体知识、任务知识、策略知识、认知体验、情感体验、组织、调节、评价、检验和管理）。问卷共有33道测试题，含两道测谎题。考虑到小学生心理发展特征，在Likert五点计分法的基础上，将调查问卷设置为四点计分法。将选项依次设置为“符合”、“比较符合”、“比较不符合”、“不符合”，分别赋值4~1分，其中测谎题分别赋值1~4分。详见表1。

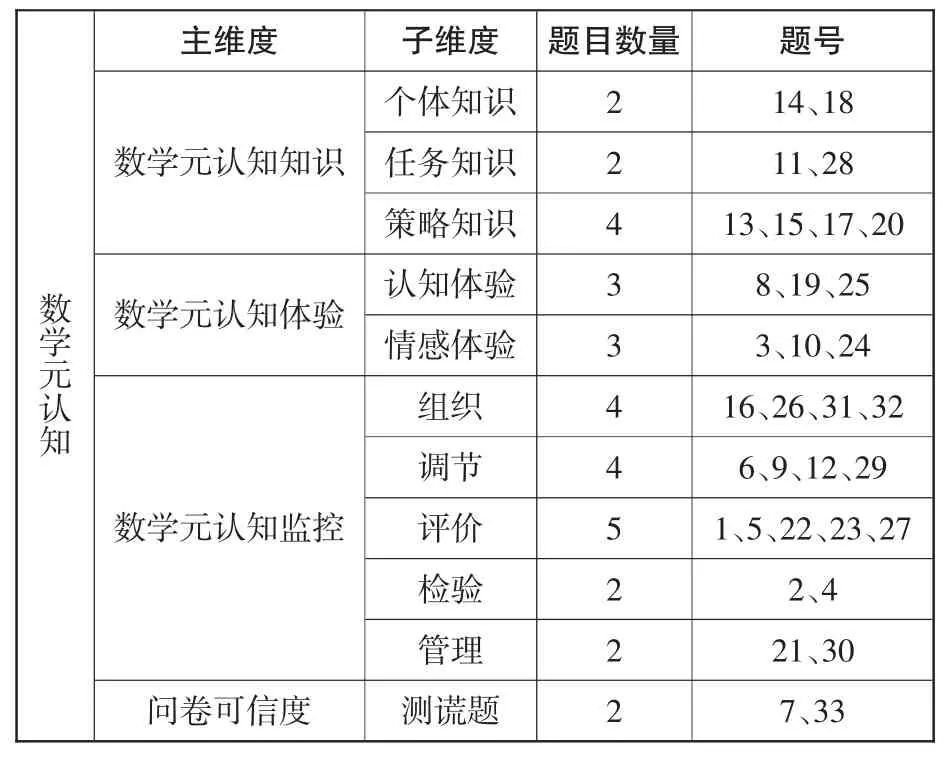
表1.题项设置

用SPSS24.0进行信效度检验，总体问卷和三个主维度的Cronbach’s Alpha值介于0.664~0.923之间，Spearman-Brown分半信度在0.650~0.878之间，重测信度参考值大于0.955。问卷与实测数据效度的Pearson积差相关系数均大于0.955，表明该问卷信度良好，内部一致性较高。此外，问卷结构合理，具有良好的结构效度。故可用作本研究的调查与测量工具。

（二）样本选取

数学元认知在小学的低年级和中年级刚开始发展，到高年级才会发展的成熟一些[16]。因此，为保证研究结果的客观性，将小学高年级学生作为调查对象，采用分层抽样法，选取天津市12个区共22所小学的高年级学生（5-6年级）进行问卷调查。由于疫情原因，本次问卷全部通过线上方式发放与回收，共回收问卷1 518份。利用测谎题删除无效问卷183份，最终确定1 335份有效问卷，问卷有效率为87.95%。数据的描述性统计分析显示样本呈正态分布，符合研究要求。

（三）数据分析与处理

测验的常模是指一个有代表性的样组（即实际受测被试样组，又称常模团体）在某种测验上的表现情况，是解释测验分数的参照系[17]。为了解被试的数学元认知在所属群体中的位置，研究构建百分等级常模和标准分常模，前者可供研究者了解被试的数学元认知水平，后者可使各维度之间的测评结果具有可比性。此外，研究还进行了数学元认知及其三个主维度的水平等级划分。

首先，采用SPSS24.0对原始数据进行统计分析，计算出天津市小学高年级学生数学元认知及各主维度的百分等级常模PR；其次，再依照正态分布表对数据进行正态化处理，将其转化为标准分数Z；再者，通过公式“T=50+10×Z”进行线性转换，确立T分数常模；最后，依据6σ原则将[-3，3]区间进行五等级水平划分，并根据操作性定义、具体测评题目及小学高年级学生的心理发展水平和认知特征，确立天津市小学高年级学生数学元认知及各主维度的水平等级标准。

二、研究结果

（一）总体水平常模

应用常模构建方法对数据进行处理和分析，建立天津市小学高年级学生数学元认知水平常模（略），确立对应的等级评价标准（表2）。为了更精准地诊断小学高年级学生数学元认知各个维度水平上的优势和不足，下面将分别建立小学高年级学生数学元认知知识、体验、监控三个子维度的常模。

表2.天津市小学高年级学生数学元认知总体水平等级表

（二）“知识”水平常模及其等级评价标准

首先，选出问卷中测试数学元认知知识的8道题目，计算样本在知识维度的总得分，按照上述方法，建立小学高年级学生数学元认知知识水平常模（略），并确定对应的等级评价标准（表3）。最后，分别计算五个等级水平下小学高年级学生数学元认知知识维度上个体知识、任务知识、策略知识三个子维度上的各个平均T值，并画出柱形图（图1）。可以发现，在数学元认知知识维度上，天津市小学高年级学生普遍不存在“优秀”等级。

表3.天津市小学高年级学生数学元认知知识水平等级表

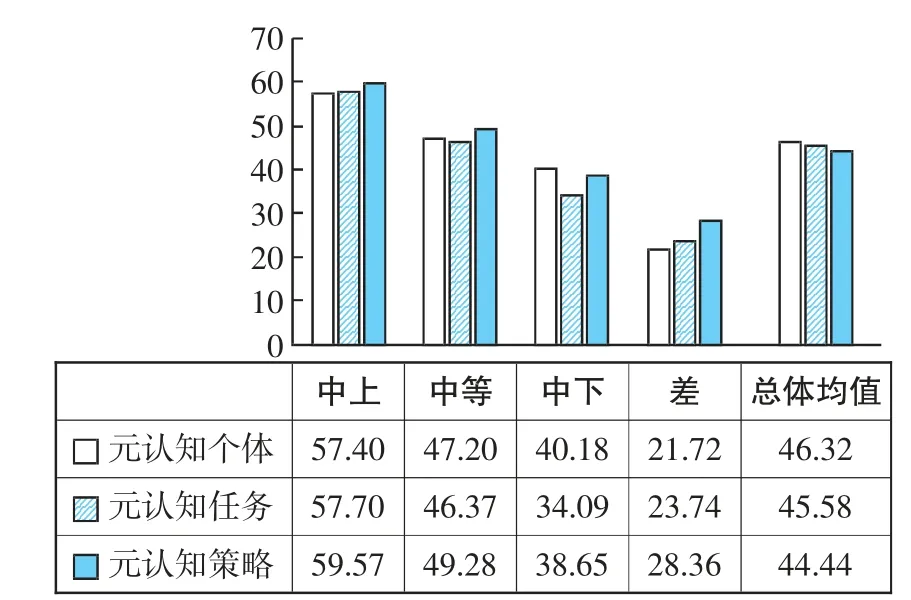
图1.知识子维度T分数柱形图

根据元认知知识子维度T分数柱形图（图1），结合问卷中与知识相关的8道问题的内容，发现不同等级小学生在数学元认知知识维度上有不同特征：优秀等级小学生能够理解和掌握数学学科知识，清晰地知道自己的学习状况、学习任务和学习目标，灵活地选择恰当的学习策略解决数学问题。中上等级小学生能够较好地掌握数学学科知识，对自身学习能力有较清晰的认识，知道学习任务、学习目标和要求，储存一定的学习策略。中等小学生能够掌握大部分数学学科知识，对任务、目标和要求的认识不够充分，可以恰当地运用部分学习策略。中下等级小学生能够理解部分学科知识，对自身的学习状况以及任务、目标和要求缺乏明确的认识，无法选择和应用学习策略。差等小学生初步了解相应的数学知识，不能认识到自身的学习状况，没有找到合适的学习策略。

（三）“体验”水平常模及其等级评价标准

使用上述相同方法，建立数学元认知“体验”水平常模（略），确立等级评价标准（表4）。最后，计算不同等级下数学元认知体验两个子维度的平均值（图2）。可以发现，在数学元认知体验上，天津市小学高年级学生普遍也不存在“优秀”等级。

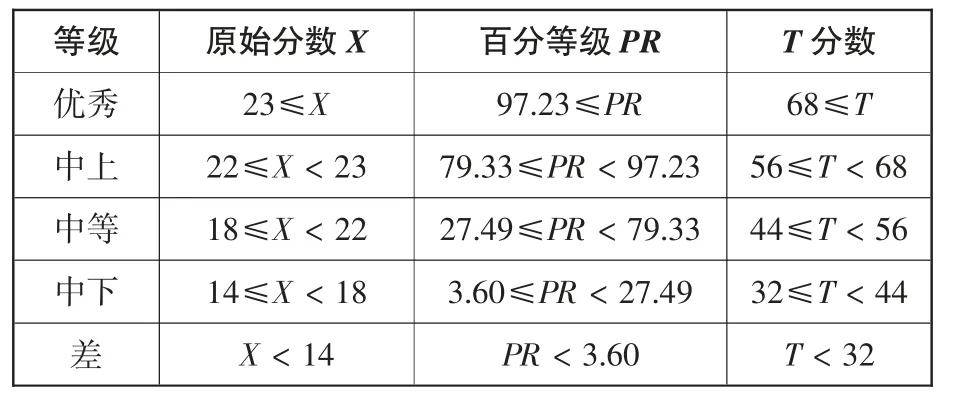
表4.天津市小学高年级学生数学元认知体验水平等级表

图2.体验子维度T分数柱形图

根据数学元认知体验的相关定义，结合问卷中与体验相关题目的内容以及小学高年级学生的认知情感特征，归纳出不同水平等级小学生在数学元认知体验维度上的具体特征：优秀等级小学生能够积极地感受到丰富的数学学习内容与学习过程，会正确地对待和改善消极的认知和情感。中上等级小学生能够获得愉快的认知体验和情感体验，具备良好的自信心。中等小学生基本能够认知到数学学习的内容与过程，具有部分积极的情感体验，能够建立数学学习的信心。中下等级小学生能够感知到学习的难易程度，会克服一些困难，但容易产生焦虑，缺乏自信。差等小学生缺乏数学学习积极的认知和情感体验。

（四）“监控”水平常模及其等级评价标准

使用以上相同的方法，建立数学元认知监控水平常模（略），制定对应的等级评价标准（见表5)。最后，计算不同等级下数学元认知监控五个子维度的平均T值（见图3）。从图中可以发现：在组织与管理、定向与计划、反思与评价这三个子维度下，天津市小学生得分没有优秀等级，说明小学高年级学生在组织与管理、定向与计划、反思与评价这三个方面的元认知监控能力比较欠缺。

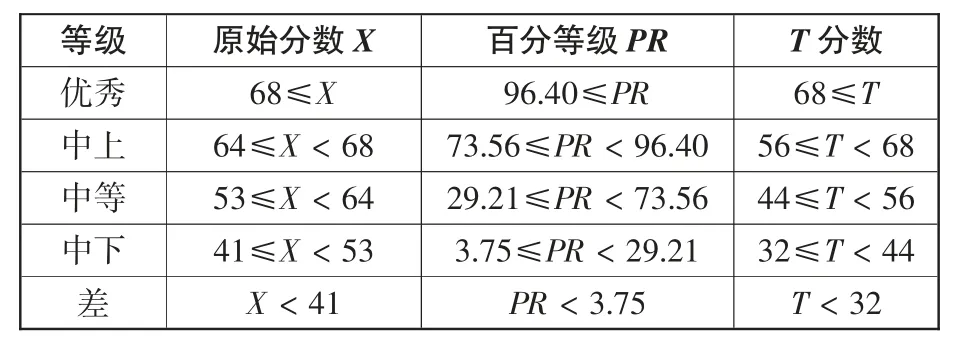
表5.天津市小学高年级学生数学元认知监控水平等级表

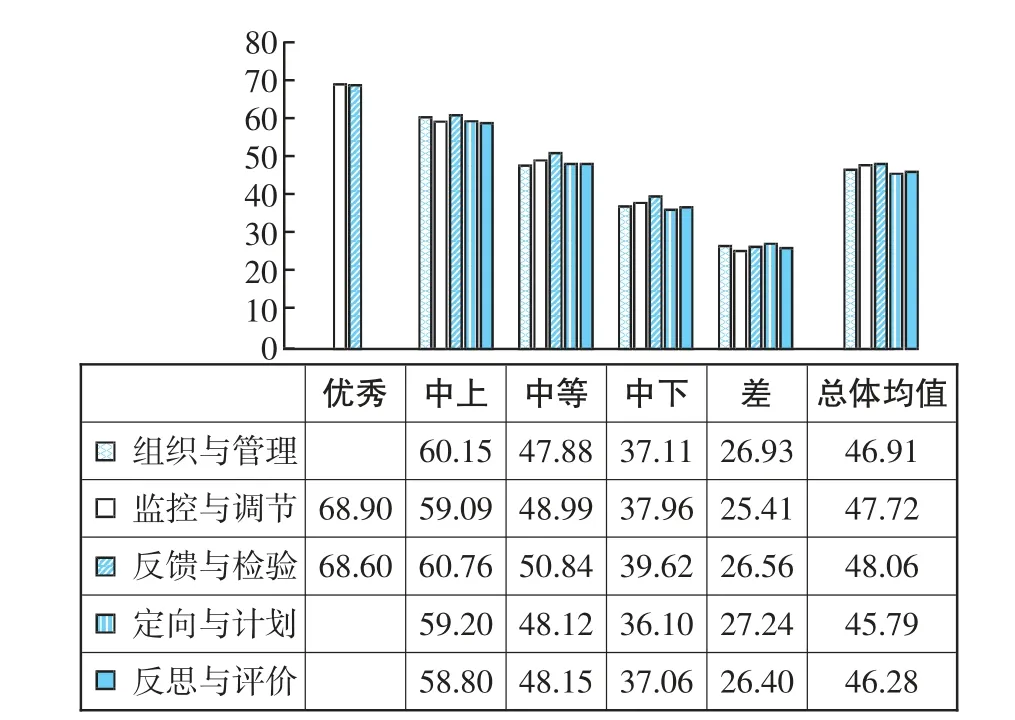
图3.监控子维度T分数柱形图

根据数学元认知监控的相关定义，结合问卷中监控题目的内容以及小学高年级学生监控能力表现，归纳出不同等级水平的小学生在数学元认知监控维度上特征：优秀等级小学生能够制定科学的学习计划、形成学习方法和习惯、诊断并评价学习成果、调控学习过程。中上等级小学生能够较好地运用和调节学习策略、会主动地反思和检验学习成果、合理评价学习过程[18]。中等小学生能够检验问题、会评价部分学习结果。中下等小学生缺乏完整的元认知监控五因子能力，无法调节学习方法，无法反思和评价整个学习。差等小学生缺乏元认知监控能力，难以监控和调节自身学习过程，不会反思和客观评价学习结果。

三、应用案例

以天津市南开区某小学六年级某普通班学生为测验对象，从班级整体和学生个体两个评估视角，对学生数学元认知水平进行测评诊断，并基于分析结果提出精准提升建议。

（一）班级应用案例分析

1.被试班级学生数学元认知水平诊断分析

被试班级有50名学生，全部进行问卷调查。剔除测谎题后，有效问卷为46份。首先，对该班学生数学元认知原始分数进行统计分析，发现：该班男生的数学元认知均值高于班级整体均值，而女生的数学元认知均值低于班级整体均值，可见该班男生的数学元认知整体水平表现比女生要好。但是，男生的数学元认知整体均值离散程度较大，说明男生之间的数学元认知总体水平差距较大。

被试班级学生整体数学元认知原始分均值为104.28，T分数为48.2，所处的百分等级为42.27，根据天津市小学高年级学生数学元认知总体水平常模（略）及等级水平表（表2）可知：被试班级学生的数学元认知整体平均水平处于天津市“中等”，超过了全市大约42%的学生。

被试班级在数学元认知三个主维度“元认知知识”“元认知体验”“元认知监控”上的T分数平均值分别为：51.60、55.08、47.20，根据主维度常模表（略）和水平等级表（表3、表4、表5）可知，各项水平均值分别超过了天津市约57%、69%、39%的小学生。整体而言，被试在数学元认知三个主维度上的水平均值皆处于天津市“中等”水平。

为了深入探索此班级“中等”水平小学生在数学元认知能力上的表现程度，计算并绘制被试班级学生与全市“中等”水平学生在数学元认知三个主维度上的T分数平均分雷达图（图4）。由图4发现，该班级学生在数学元认知知识、体验、监控三个主维度上都整体高于全市中等平均水平，尤其是在数学元认知体验和数学元认知监控上远远高于全市中等平均水平。相比之下，被试班级学生数学元认知知识平均水平较为薄弱，仅仅略高于全市中等平均水平。

为了精准找到问题所在，进一步诊断分析该班级学生数学元认知知识水平，计算并绘制数学元认知知识的三个子维度T分数雷达图（图5）。由图5可知：该班学生个体知识比全市中等学生的整体水平略好，而关于任务与策略的知识则没有达到全市中等学生的整体水平。

图4.被试学生与全市中等水平学生数学元认知主维度雷达图

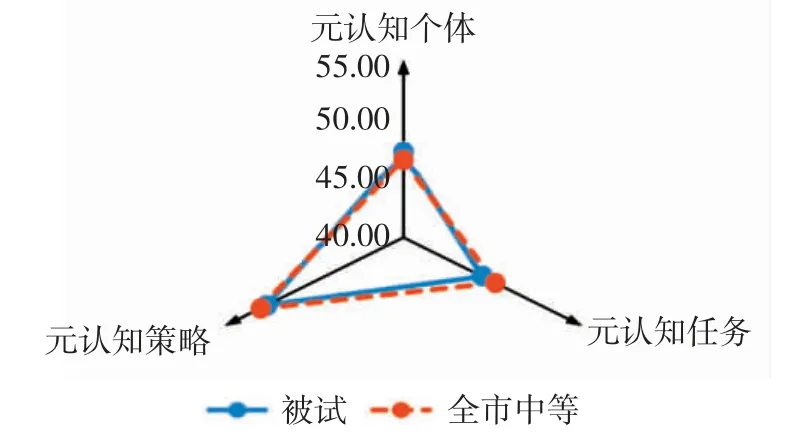
图5.被试学生与全市数学元认知知识维度雷达图

2.被试班级数学元认知水平改进建议

任务维度提高措施：教师可以鼓励学生自主寻找研究问题及解决问题的方法。通过任务设置和课堂追问等方式，有效启发学生的数学思维，启迪学生明确数学学习任务。

策略维度提高措施：教师可以借鉴乔治·波利亚（George Polya）《怎样解题表》，提高学生对策略知识的认知水平。依据“弄清问题→拟定计划→实现计划→检验回顾”的四个环节[19]，教师循序渐进地培养小学生的数学思维能力，鼓励学生独立思考，应用数学知识和技能，选择恰当的数学策略。

（二）个体案例分析

1.被试个体数学元认知水平诊断分析

被试学生数学元认知水平的原始总分是109，各个子维度的T分数分别为：51.6（元认知知识）、63（元认知体验）、47.2（元认知监控）。对照总体常模和三个主维度常模等级表可知，在天津市小学高年级学生中，该学生数学元认知总体水平位于中等。具体到子维度可发现，该生在体验维度上位于中上等水平，但是在知识和监控维度上位于中等水平。可见，该学生数学元认知体验水平表现较好，但数学元认知知识和监控水平表现不佳。

为了找到该生数学元认知知识和监控水平表现不佳的具体原因，下面对该生数学元认知知识和监控维度进行深入分析，并与全市小学高年级学生数学元认知体验和监控中等水平相比较，具体雷达图见图6、图7。

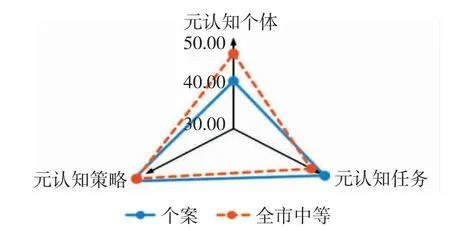
图6.个案数学元认知知识维度雷达图

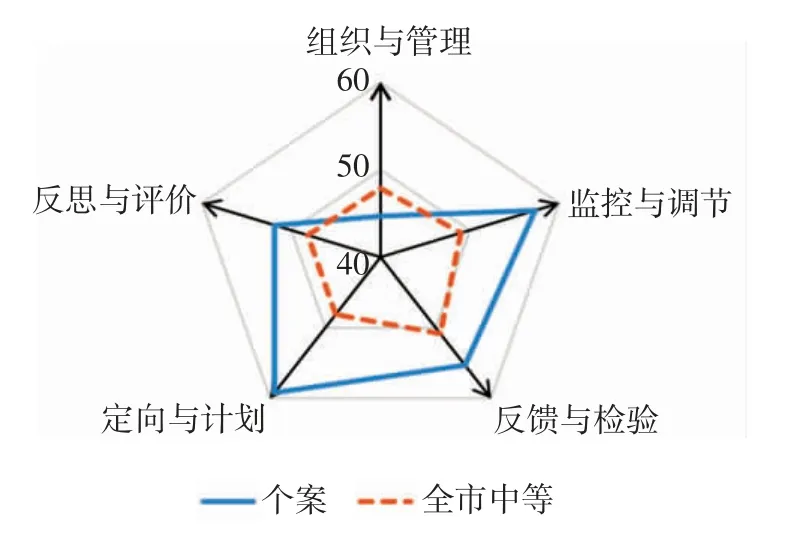
图7.个案数学元认知监控维度雷达图

由图6、图7发现，在元认知知识维度上，该生关于任务的知识比全市中等水平学生更丰富，关于策略的知识与全市中等水平相一致，但是关于个体的知识有所欠缺；监控维度上，组织与管理水平有所欠缺，但是在其他四个子维度上都表现良好，而且都优于全市中等学生水平。

2.被试个体数学元认知干预训练

已有研究发现，对小学生进行元认知训练，不仅能够提高学生的元认知水平，还能够有效地提高学生的数学成绩[20][21][22]。基于研究结果，联系数学教师对被试学生进行干预训练。经过一个月的指导，再重新测试该生的数学元认知水平，发现该生的数学元认知整体水平以及知识和监控两个子维度的得分都有所提升，尤其是知识维度，从中等水平提升到了中上等水平。被试学生一个月后的数学成绩较一个月前有了显著提升。

被试班级的数学教师认为应用常模能够有效地评价出学生的数学元认知水平。通过本研究所构建的水平常模表和等级评价表，能够获得每一位被试学生在本班乃至天津市所处的相对位置，精准发现学生在数学学习中的不足以及今后需要重点提高的方向。被试学生认为通过常模，能够获得自己在班级乃至天津市小学高年级学生中所处的相对位置，清楚地认识到了自己的数学元认知水平以及各个维度下的等级特征，并且描述得较为准确。经过教师的针对性指导和干预训练后，数学学习效率和学习成绩得到了明显改善，自身的整体数学元认知水平得到了显著提升。

四、讨论

与已有的天津市初中生、高中生数学元认知水平常模研究[23][24]相比，本研究有两个新的发现：第一，研究发现小学高年级学生的数学元认知水平整体偏低，只有“监控与调节”和“反馈与检验”这两个元认知监控子维度下存在少量优秀等级的学生，其他子维度下大部分学生处于中上等和中等水平，少数学生处于中下等水平以下。换言之，天津市小学高年级学生的数学元认知水平整体处于中等，优秀学生占比很少，各个子维度也都普遍低于初中生和高中生的数学元认知水平。王光明等关于小学高年级学生数学学习非智力因素常模及应用案例研究也发现小学高年级学生认知动机和情绪稳定性表现不足[25]。这与欧慧谋、唐剑岚的研究发现相一致[4]。这说明小学高年级学生的数学元认知水平发展尚未成熟，还有很大的发展空间。但是，小学高年级学生的监控调节能力和反馈检验能力较好，这可能和“以考促学”的教学模式有关。在数学学科中，教师经常通过考试来检验学生的数学学习效果，各种课堂小测、周考、月考等教学评价方式依然普遍存在，所以学生通过考试的方式调节监控数学学习的能力整体较为突出。第二，本研究还发现，在教学中对小学生进行数学元认知训练，可以有效提高学生应用题解题能力，其效果明显优于一般思维策略训练。这一结论与国内外关于元认知训练的已有研究结果一致，即元认知训练是提高教学质量的有效手段[26]。

与已有的天津市初中生和高中生数学元认知常模研究相比，本研究对水平等级表做了改进，对数学元认知各个维度上不同等级学生的描述更加符合小学生的特征，更有利于施测者应用常模进行测量与评价。

本研究还存在一些局限。首先，常模本身存在的局限性。因为选取的是某一地区某一时期的样本，所以建立的常模具有区域性和时效性。由于教育的不断发展以及不同地区教育水平的差异性，本研究所建立的常模不能普遍性地适用于天津市以外的其他地区，也不能长期性地适用于被测区域内。其次，研究对象自身的局限性。无论是从理论上还是从整体的调查结果来看，小学生的数学元认知水平整体上还处于中等及以下的水平。调查对象数学元认知能力发展的不足，在一定程度上影响了研究结果的有效性。