负泊松比锚杆/索力学特性及其工程应用1)
2022-03-12何满潮宫伟力
何满潮 杜 帅 宫伟力, 聂 雯
∗(中国矿业大学(北京) 深部岩土力学与地下工程国家重点实验室,北京 100083)†(中国矿业大学(北京) 力学与建筑工程学院,北京 100083)
∗∗(滨州学院建筑工程学院,山东滨州 256600)
††(河北工业大学土木与交通学院,天津 300401)
随着开采深度的增加和开采规模的增大,矿山岩体稳定性问题对煤炭资源的开采提出了严峻的挑战,大型露天矿的边坡失稳、深部开采中顶板垮落、冲击地压、瓦斯突出、岩爆等工程地质灾害的机理无法被全面认识,一直是困扰矿山岩体力学的重大难题[1]。一方面,深部岩体本构关系的强非线性使得这些灾害的发生机制非常复杂,经典的岩石力学理论难以准确地运用;另一方面,工程灾害难观测且数据获取不充分,给基于现场监测数据的统计与反演分析带来很大的困难。因此需要研发新的装置,提出新的概念将复杂的矿山岩体本构关系从未知转化为已知,实现矿山岩体大变形和动力灾害的机理认知和控制预测。
锚杆系统按其力学特性可分为三类[2],即:刚性锚杆、延性锚杆和吸能锚杆。刚性锚杆的强度较高,可以及时提供支护力,但变形能力小。延性锚杆的变形能力较强,但刚度与支护力较小,如Split-set[3]等。吸能锚杆是近年来为了控制矿山岩体中的大变形和动力灾害而新发展的锚杆类型[2]。与其他两类锚杆力学特性不同,吸能锚杆不仅具有较高的承载力,且具有较大的变形能力[4]。吸能锚杆按其变形机制一般可以分为两类[5]:一种是设计特殊锚固点,利用锚固点与填充砂浆的摩擦阻力和锚杆杆体的塑性变形来吸能,如D-bolt[6],Cone-bolt[7]等;另一种是设计特殊的结构,利用锚杆杆体与结构的摩擦阻力来吸收能量,如Garford[8],Roofex[9]等。这些吸能锚杆在控制围岩大变形或者冲击载荷引起的灾害方面显示出优越性,但由于其支护力随位移的变化而呈现出“弹性、强化和软化” 等阶段,难以完全满足岩体大变形支护的要求[10]。
为了解决矿山岩体工程中支护的需求,Cai 等[4]和何满潮等[10-11]研发了具有负泊松比效应的恒阻大变形锚杆(constant-resistance-large-deformation bolt,简称CRLD bolt 或称He bolt)。因其核心吸能装置变形具有负泊松比(negative Poisson’s ratio, NPR) 效应,又称为负泊松比锚杆 (NPR 锚杆)[12]。NPR 锚杆具有拉不断、高恒阻力、理想弹塑性等超常材料特性,是一种新型吸能锚杆,与常见吸能锚杆不同,其恒阻力主要与负泊松比装置的材料结构特性有关,与外载和岩体性质无关[12]。单根及多根NPR 锚杆的霍普金森冲击试验结果表明NPR 锚杆在冲击载荷下,仅发生可控变形,具有抗冲击能力[13]。在实际工程应用中,NPR 锚杆分为巷道与隧道支护用NPR 锚索(恒阻力最大达500 kN)与滑坡控制用锚索(恒阻力最大达900 kN),因此也统称为NPR 锚杆/索。NPR 锚杆/索在冲击地压控制[14-16],巷道大变形控制[17-20],大型露天矿滑坡监测预警[21-23]等工程中得到了广泛应用。
NPR 锚杆/索嵌入岩体后,会形成具有负泊松比支护效应的支护岩体,称为“负泊松比岩体(NPR岩体)”;NPR 岩体在外部载荷作用下,NPR 锚杆/索与岩体相互作用时发生协同变形,其力学行为具有NPR 效应;由于NPR 锚杆/索具有内禀的近似理想弹塑性本构关系,可以对岩体的力学行为进行降维与解耦分析,将岩体的复杂非线性、非可测性力学行为转化为简单、可探测的力学行为[10,24]。本文简要介绍了NPR 锚杆的静力学与动力学本构关系、NPR锚杆与岩体相互作用的机理,以及NPR 锚杆/索在深部矿冲击地压控制和滑坡灾害监测预警中应用的部分研究成果。
1 NPR 岩石力学基本原理
NPR 材料又称拉胀材料,其力学特性是由材料的内部结构所决定的。图1 为典型的NPR 材料,当受到轴向拉力时,其内部的内凹型蜂窝结构发生横向的膨胀变形,产生NPR 现象。文献[25] 证明,NPR现象存在于不同尺度下(见图2),既可以由材料性质产生,也可以通过宏观结构实现。

图1 蜂窝结构材料的NPR 现象[25]Fig.1 NPR phenomenon in honeycombs structured materials[25]
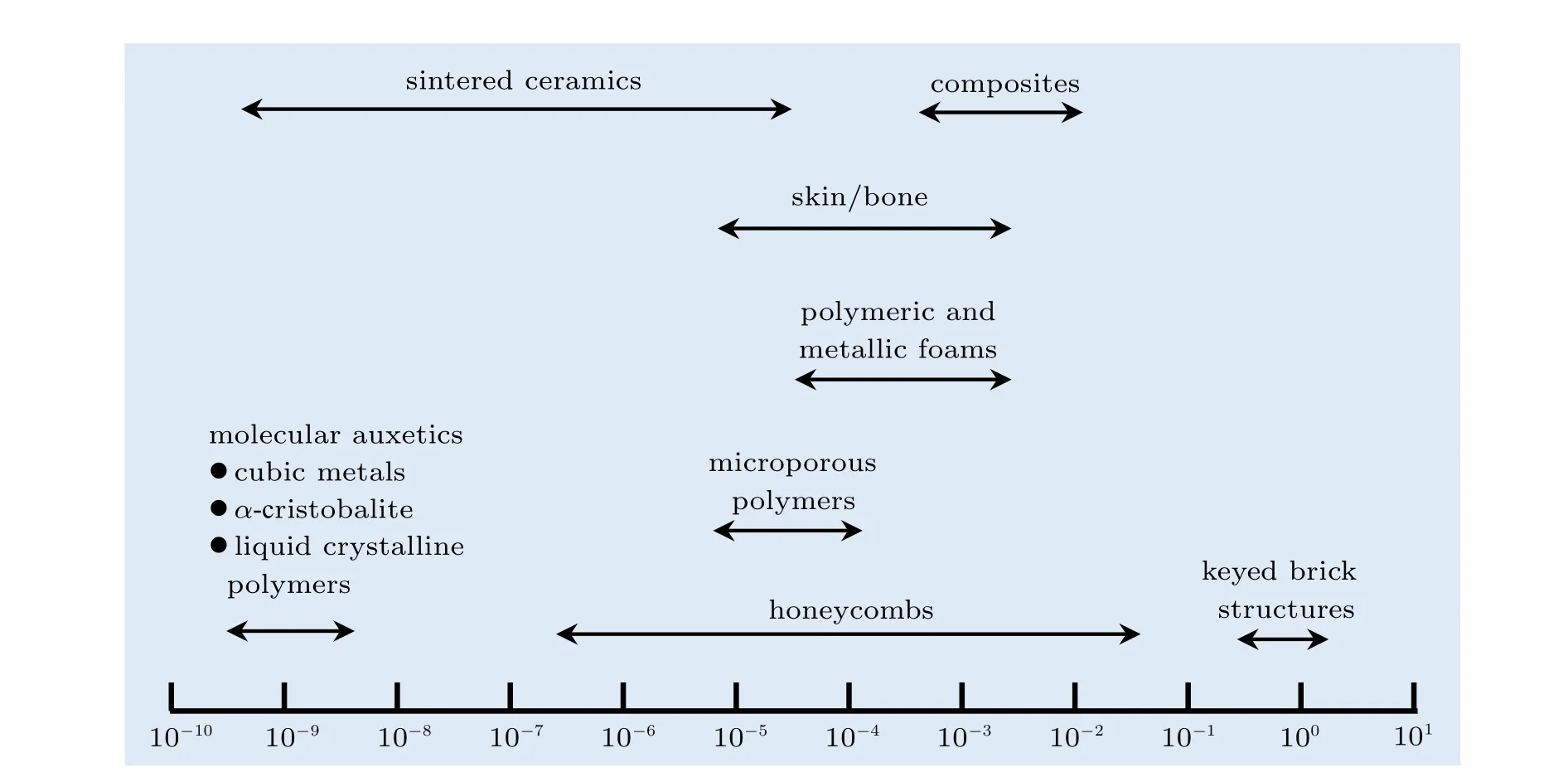
图2 不同尺度下的NPR 现象[25]Fig.2 NPR phenomenon at different scales[25]
NPR 锚杆由杆体、锥体、套筒、托盘与紧固螺母组成,如图3 所示。NPR 锚杆的锚固端固定于岩体中,杆体与锥体连接,锥体套于套筒之中,锥体小端略小于套筒内径,大端略大于套筒内径,利用托盘和紧固螺母将套筒固定在自由面。当自由端受到轴向载荷向外拉伸,锥体与套筒之间可以发生相对滑移,使得NPR 锚杆发生结构伸长变形。在拉伸过程中套筒受到锥体挤压发生径向膨胀,即产生宏观NPR 结构效应。

图3 NPR 锚杆基本结构与工作原理Fig.3 Structure and working principle of NPR bolt
采用小扰动控制的方法,将已知力学特性的人工材料嵌入地学系统中,可以将地学系统的复杂非线性力学行为进行降维分析,转化为可探测的、确定性行为。基于上述思想,将具有NPR 效应的支护材料嵌入工程岩体中,可以实现将岩体原有的复杂非线性本构关系,转换为近似的理想弹塑性本构关系,从而开展对岩体力学行为进行认知和探测的研究。
2 NPR 锚杆静力学本构关系
2.1 NPR 锚杆的恒阻力
NPR 锚杆的恒阻力主要由锥体与套管之间的滑动摩擦力提供,其结构物理模型如图4 所示。假定锥体为刚体,套管在锥体运动时发生径向膨胀弹性变形,产生径向压力,导致套筒与锥体之间产生摩擦力。套筒与锥体之间能提供的轴向最大摩擦阻力称为临界阻力P0,可表达为[12]

图4 NPR 锚杆的恒阻力结构原理[12]Fig.4 Constant resistance structure of NPR bolt[12]

式中f为套筒与锥体之间的静摩擦力系数,IS为套筒材料参数,IC为锥体几何参数,按下式计算
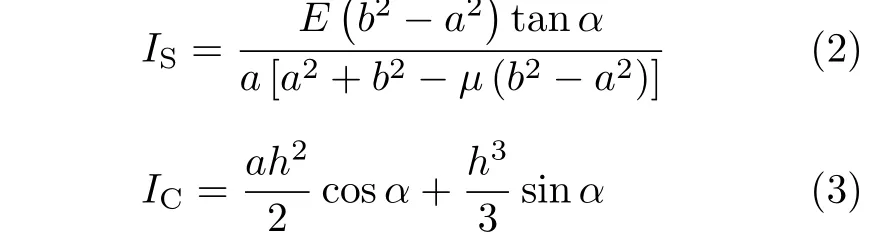
式中,α为锥体斜面倾角,h为锥体长度,a和b分别为锥体小端、大端直径,E和µ分别为套筒的弹性模量和泊松比。
根据式(1),NPR 锚杆的锥体与套筒之间最大阻力P0只与摩擦系数f、材料参数IS和几何参数IC相关,与外载荷无关,所以P0又称为NPR 锚杆的恒阻力。矿山开采后,发生向临空面外的变形,导致锚杆产生拉力并通过锥体作用在套筒上,在锥体和套筒界面产生相对滑动趋势,当拉力超过NPR 锚杆的恒阻力P0时,套管将沿自由端输出锚杆位移。
2.2 NPR 锚杆的静力学模型
NPR 锚杆是由杆体、锥体、套筒等多个构件组成的复合结构,可简化为由胡克体与粘滑单元(H-G单元)串联组成的两元件模型[12](见图5),其中胡克体代表锚杆杆体(刚度为k),H-G 单元代表NPR 结构(具有粘滑本构关系,与NPR 结构的滑移摩擦性质有关)。当外载荷小于恒阻力时,杆体发生弹性变形,达到恒阻力后发生结构屈服,可在静载条件下发生大变形而不失效。

图5 NPR 锚杆静力拉伸力学模型[12]Fig.5 Static tensile mechanical model of NPR bolt[12]
令锚杆以匀速v发生位移x=vt,初始阶段内,锥体与套筒保持相对静止,锚杆首先发生弹性变形,拉力P随位移x线性增加,最大位移为x1=P0/k。在P=P0时锥体与套筒开始发生相对滑动,进入滑移阶段,锥体在弹性力与滑动摩擦力作用下发生振荡运动,杆体弹力随变形相应减小。在准静态加载过程中,杆端速度v相对于锥体振动可忽略。当锥体速度为零时,锥体与套筒停止相对运动,拉力达到最小值,此拉力即为下限恒阻力[12]

锥体与套筒停止相对运动后,进入粘滞阶段。拉力继续随杆端位移匀速增加,直至达到恒阻力。此后再次进入滑移阶段,随着杆端位移的不断增加,NPR锚杆会继续重复粘滑阶段的循环,一个循环周期内发生的位移为Δx。循环位移和极限恒阻力之间的关系为
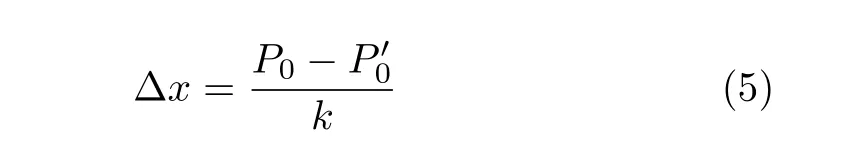
由此可得准静态张拉载荷P与锚杆位移x的关系,即NPR 锚杆的静力本构方程[12]



图6 NPR 锚杆在静载作用下的本构关系[12]Fig.6 Constitutive curve of NPR bolt under static load[12]
3 NPR 岩体动力学本构关系及冲击地压控制
3.1 NPR 锚杆动力学本构关系
NPR 锚杆在深部巷道围岩支护时通常为多根锚杆的并联组合支护形式,基于NPR 锚杆的静力拉伸元件模型(见图5),通过并联NPR 锚杆建立相应动力学本构关系。在冲击动力载荷作用下,NPR 锚杆的动力学本构关系需要充分考虑锥体与套筒惯性力的影响,锚杆在冲击之后的变速运动情况总体可分为三个阶段,即弹性变形阶段、结构变形阶段和回弹阶段(见图7)[26]。

图7 双NPR 锚杆动力载荷作用下力学模型[26]Fig.7 Mechanical model for double NPR bolts under dynamic load[26]
在冲击载荷作用初期,杆体仅发生弹性变形,当位移达到x1=P0/k,弹性力达到恒阻力P0,锚杆开始发生结构变形。结构变形阶段内锥体和套筒处于相对滑移状态,两者位移不同步,套筒在冲击载荷P(t)与滑动摩擦力Pd=2πfdISIC作用下加速运动,而锥体在弹性力T和滑动摩擦力Pd作用下发生振荡运动,直到两者相对速度减为零时结束。结构变形阶段结束时套筒与锥体的相对位移记为Δxd。此后两者在杆柄弹性力T作用下整体发生回弹振荡,由于结构必然存在阻尼影响,NPR 锚杆的动能会逐步消散,稳定时的最终伸长量即为Δxd。
基于NPR 锚杆的冲击动力学本构模型,得到冲击载荷作用下NPR 锚杆的力学响应曲线(见图8),其运动过程呈现出明显的惯性效应[26]。NPR 锚杆的位移在结构变形结束时达到峰值的时间明显滞后于载荷达到峰值的时间,这主要因为套筒与锥体在载荷达到峰值后由于惯性效应继续发生运动,冲击载荷结束后锚杆也在惯性力作用下继续振动,直至动能被阻尼消耗后锚杆达到稳定伸长量(见图8(a))。由NPR 锚杆在冲击动力载荷作用下的位移-载荷曲线(见图8(b)) 可知,载荷峰值位置与位移峰值位置并未重合,载荷结束的位置与最终稳定的位置也不相同,而且位移在载荷结束前存在回缩现象。
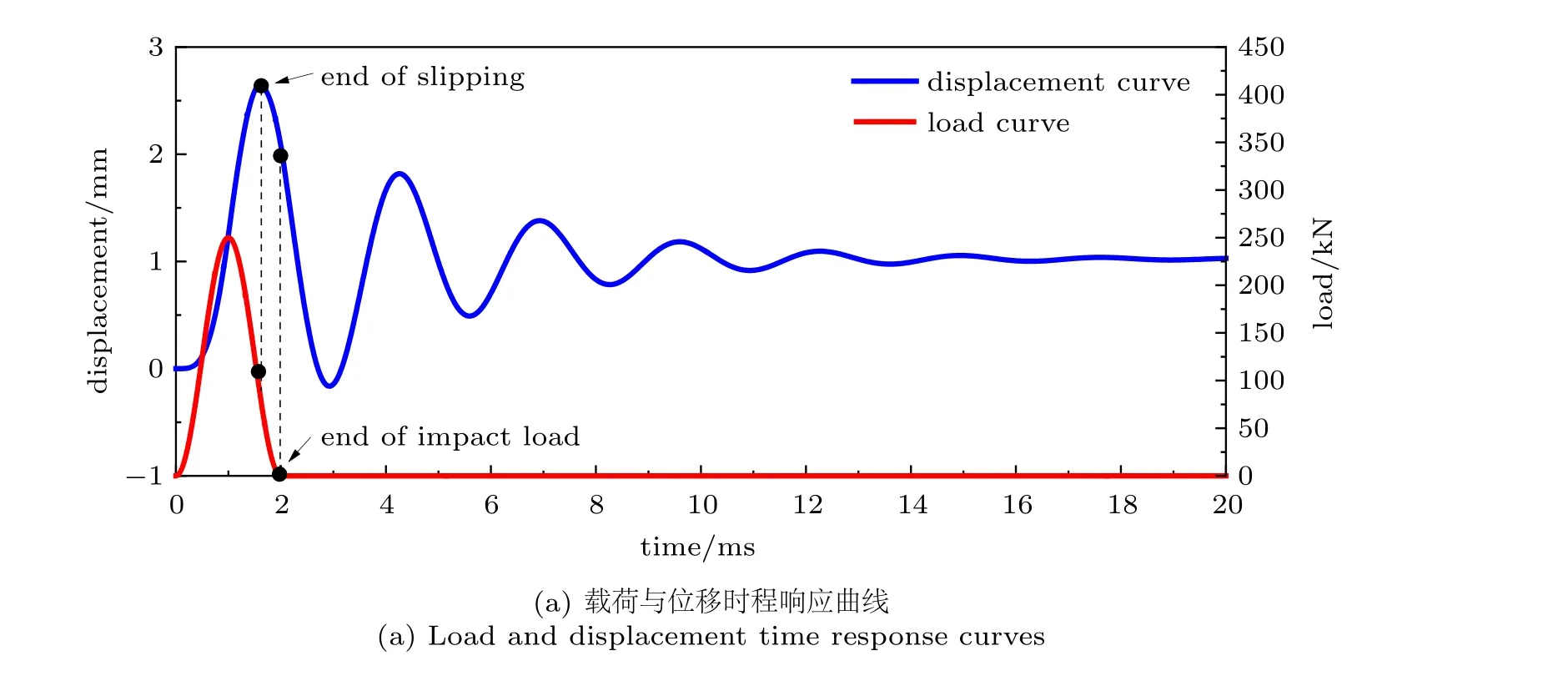
图8 双NPR 锚杆在稳定冲击载荷作用下的本构关系[26]Fig.8 Constitutive relationship of double NPR anchors under impact load[26]

图8 双NPR 锚杆在稳定冲击载荷作用下的本构关系[26](续)Fig.8 Constitutive relationship of double NPR anchors under impact load[26] (continued)
3.2 NPR 锚索在冲击地压控制中的应用
已经开展的落锤冲击[27]和SHTB 冲击[28]等动力载荷试验表明,NPR 锚索具有吸收冲击能量均匀、防冲击性能良好等特点,适用于冲击地压灾害的防治。以沈阳的红阳三矿防冲击实验[16]为例,此矿区开采深度超千米,深部的高构造应力使得巷道开挖过程中冲击动力学现象频发,为更科学地指导NPR 锚索在冲击地压防止中的应用,在矿区现场进行了NPR 锚索与普通锚索的防冲性能对比试验。
试验段选在-850 水平1213 回风联络巷,在相同地质条件下,在原锚网索支护的基础上对左帮进行间撑距800 mm×1000 mm 的上、中、下三排锚索加强支护,I、IV 试验段采用6500 mm 长的普通Φ21.7 mm 锚索,II、III 试验段采用350 kN 高恒阻NPR 锚索,布置图如图9 所示。试验通过爆破模拟冲击地压破坏作用,对比其支护防冲效果。

图9 试验段加强支护布置图[16]Fig.9 Test section and reinforcement support arrangement[16]
结果显示,在10 kg 炸药爆破中,普通锚索支护段出现1.8 m 爆坑,且部分锚索被冲断,而NPR 锚索支护段爆破前后无溃帮现象,NPR 锚索的最大拉伸变形为57 mm (见图10)。通过对比,与普通锚杆段出现整体垮塌不同,NPR 锚索段在冲击力作用下产生瞬间滑移,在结构屈服的过程中吸收了爆炸产生的冲击能量,最终只产生有限的可控变形,保证了巷道的整体稳定,进而验证了NPR 锚索优异的抗冲击性能。

图10 NPR 锚索冲击后拉伸量[16]Fig.10 Post-impact tensile displacement of NPR cable[16]
4 NPR 锚杆与岩体相互作用机理及大变形控制
4.1 NPR 岩体的本构关系
广义开尔文体常用来表征具有流变性质的岩体[29-30],由弹性模量为EH的胡克体与弹性模量为EK、黏滞系数为η的开尔文体串联组成。普通锚杆在支护过程中可以简化为弹性模量为Eb的胡克体模型,其内端固定于岩体中,外端与岩体表面紧密接触,岩体与锚杆在外力σ作用下发生同步变形,满足流变微分理论中的并联法则,从而建立普通锚杆锚固岩体的一维流变本构模型(见图11)。NPR 岩体同样满足并联法则,即NPR 岩体的应力值实际为岩体与NPR 锚杆的应力之和,将锚固岩体中代表普通锚杆的物理模型替换为NPR 锚杆元件,可得到NPR岩体的本构模型(见图12)。
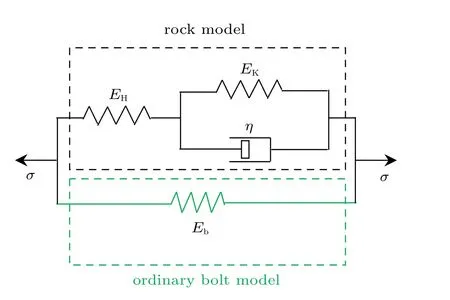
图11 普通锚杆锚固岩体的本构模型[23]Fig.11 Constitutive model of rock anchored by ordinary bolt[23]

图12 NPR 岩体的本构模型Fig.12 Constitutive model of NPR rock
4.2 NPR 岩体的力学响应
深部岩体在开采过程中的受力情况可以通过恒定载荷的形式进行模拟,普通锚杆支护岩体与NPR岩体在恒定载荷作用下的本构关系如图13 所示。在恒定载荷作用下,普通锚杆支护岩体保持应力不变,应变持续增加,当达到锚杆变形极限则必然导致锚杆断裂失效;而NPR 岩体的应力则随应变的增加而表现出阶梯型下降的让压变形特征,变化周期与NPR 锚杆粘滑运动存在对应关系。NPR 岩体在黏滞阶段应力不变而应变增加,在滑移阶段因NPR 锚杆出现结构屈服而出现应力减小,说明NPR 锚杆可在岩体发生大变形的情况下起到让压效果,并且持续提供支护作用力。
由图 13 可见,由于具有了负泊松比结构效应,NPR 岩体在外载荷(静载) 的作用下,具有了不同于岩石材料性质的让压型本构关系;同时,NPR锚杆仍然具有粘滑型本构关系,其上限值恒定不变(即NPR 锚杆的恒阻力)。因此,NPR 岩体在外载荷作用下的应力重分布的增量,可以通过与NPR 锚杆恒阻力间的差值进行计算;根据NPR 岩体应力重分布的增量的分析,可实现对NPR 岩体力学行为的认知,进而实现对岩体复杂非线性本构关系的降维与解耦分析,以及岩体力学行为的预测,即岩体的复杂非线性系统的“小扰动控制”。

图13 阶跃载荷作用下锚固岩体的应力应变本构关系Fig.13 Stress-strain relationship of anchored rock under step load
5 NPR 岩体力学在滑坡预测中的应用
5.1 双体灾变力学原理
地震与滑坡是地学系统主要的两种地质灾害,其发生过程中常伴随着地表位移、地下水位等参数的改变,然而这些只是灾害发生的必要条件。为探索地质灾害监测预警的有效方法,揭示其发生的充分必要条件,何满潮等[31]提出了地质灾害的双体灾变力学模型(double block system,DBS)(见图14)。
自然地震是由板块挤压作用下地层构造带中上盘与下盘相对运动引起 (见图 14(a)),滑坡灾害是重力作用下滑坡体与滑床之间的相对运动 (见图14(b)),双块体的相对运动是灾害发生的本质特征,故统称为双体灾变。结合双体灾变过程中的运动特点可以发现,双块体发生相对运动的充要条件是其界面上的相互作用力发生变化,双体上下盘发生相对机械运动时,在滑动面上作用的机械力符合牛顿定律,也称为“牛顿力”。对于滑坡DBS,若滑动面两侧下滑力T1大于抗滑力T2,则滑坡灾害必然发生。

图14 双体灾变力学模型[31]Fig.14 DBS mechanical model[31]
根据NPR 岩石力学的基本原理,在天然地学系统中嵌入人造NPR 构件,可实现滑坡体中滑动面上相互作用力的间接测量。在边坡支护工程中,将具有北斗卫星远程通讯功能的力学传感器安装在NPR锚索自由端,组成具备现场支护与远程监测等多重功能的边坡牛顿力监测系统(Newton’s force monitoring system, NFMS),从而实现对滑坡灾害的预测。
对于受锚固边坡,当其处于极限平衡状态(图15) 时,水平方向的受力满足方程[31]

图15 滑坡DBS 中NPR 岩石力学机理[23]Fig.15 Mechanics of NPR rock in landslide DBS[23]

式中,θ为NPR 锚索与水平面夹角(°),α为滑动面与水平面夹角(°),A为滑动面的面积(m2),G为滑坡体自重(kN),c和φ分别为滑坡体黏聚力(kPa)和内摩擦角(°)。
5.2 基于牛顿力的滑坡预测
我国是滑坡灾害分布最广、损失最严重的国家之一,基于NPR 锚索的NFMS 已经成功应用于我国12 个省内的二百余个边坡工程,通过牛顿力监测提供滑坡预报[23]。以南芬露天铁矿为例,该矿区位于辽宁省本溪市,是亚洲最大的单体露天铁矿之一,矿体赋存于太古界鞍山群含铁岩段中,呈单斜构造。由于长期露天开采,此处形成高大边坡的巨大隐患,1960 年以来发生六余次滑坡灾害,变形情况十分严重,成为滑坡研究的重点区域[32]。
根据南芬露天铁矿的老滑坡体结构与规模,将28 个NPR 锚杆力学监测站点布置于334~662 m台阶之间(见图16),并在较稳定的边坡上盘设置北斗卫星中继站、降水监测点和数据转发中心,构成 NFMS 系统。系统开始工作后,成功预测了“20100731” 和“20111005” 等多次滑坡灾害,为现场的安全生产提供了有利保障[23]。

图16 NPR 锚索滑坡监测布置图[23]Fig.16 NPR cable landslide monitoring arrangement[23]
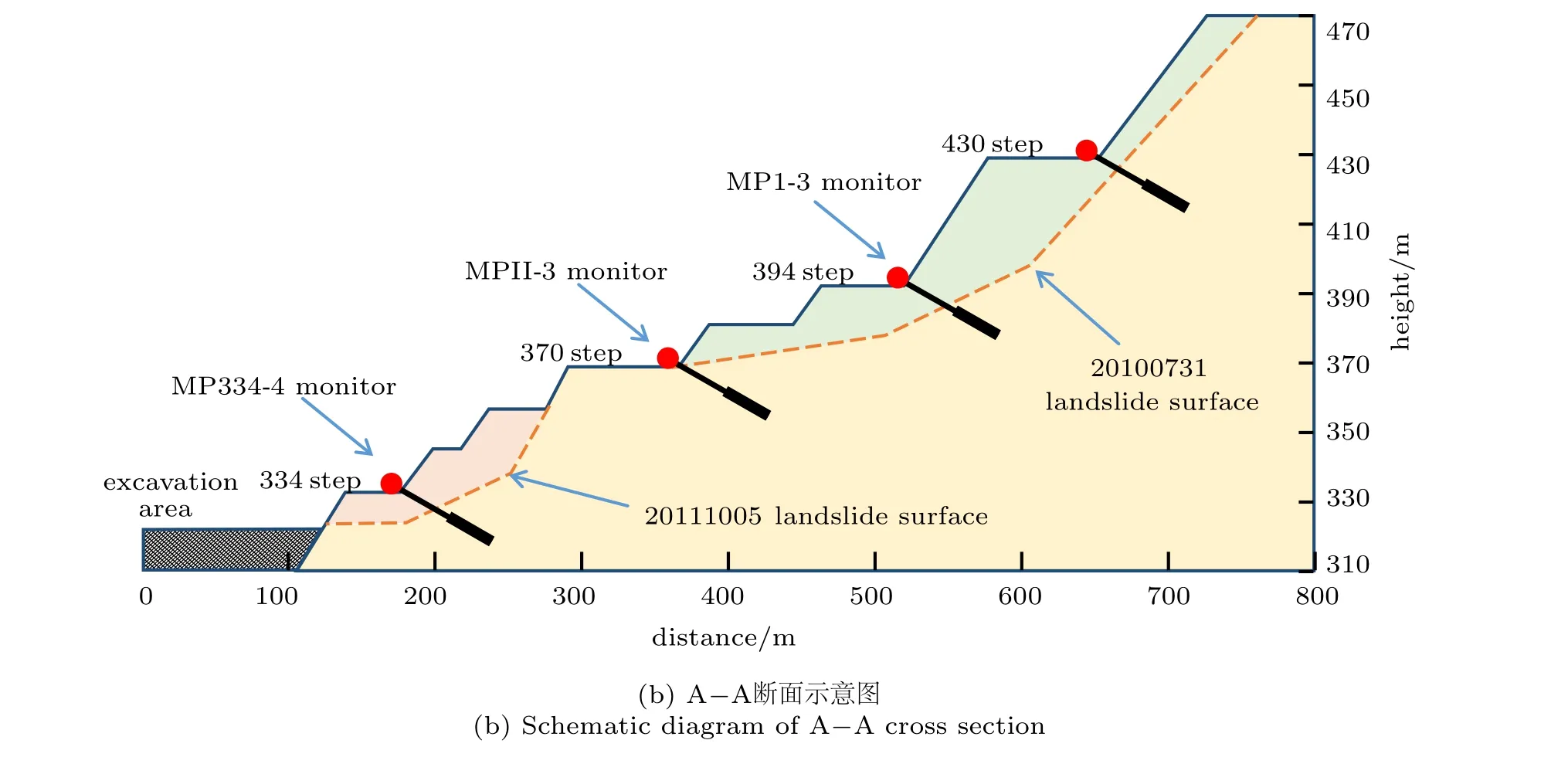
图16 NPR 锚索滑坡监测布置图[23](续)Fig.16 NPR cable landslide monitoring arrangement[23] (continued)
结合系统记录的监测力与降雨量的耦合监测曲线[23](见图17),334 m 台阶监测点实现了“20111005滑坡” 的成功预警。2011 年10 月1 日前,监测力曲线呈稳定状态,此后开始逐渐上升;10 月3 日凌晨出现高达400 kN 的增量,NFMS 系统发出黄色预警信号,矿区下达停采命令并进行人员与设备疏散;当日下午监测力曲线增至约1100 kN,系统发出橙色预警信号;10 月4 日监测力曲线增至1400 kN,系统发出红色预警信号,现场出现大量碎石滚落;10 月5 日出现集中降雨,监测力曲线从1700 kN 骤降至1400 kN,322~358 m 台阶处出现高36 m,宽5 m的滑坡灾害。10 月7 日,检测力曲线进入稳定状态后,矿区恢复开采,此次基于NFMS 系统的滑坡预测有效地避免了人员伤亡与财产损失。
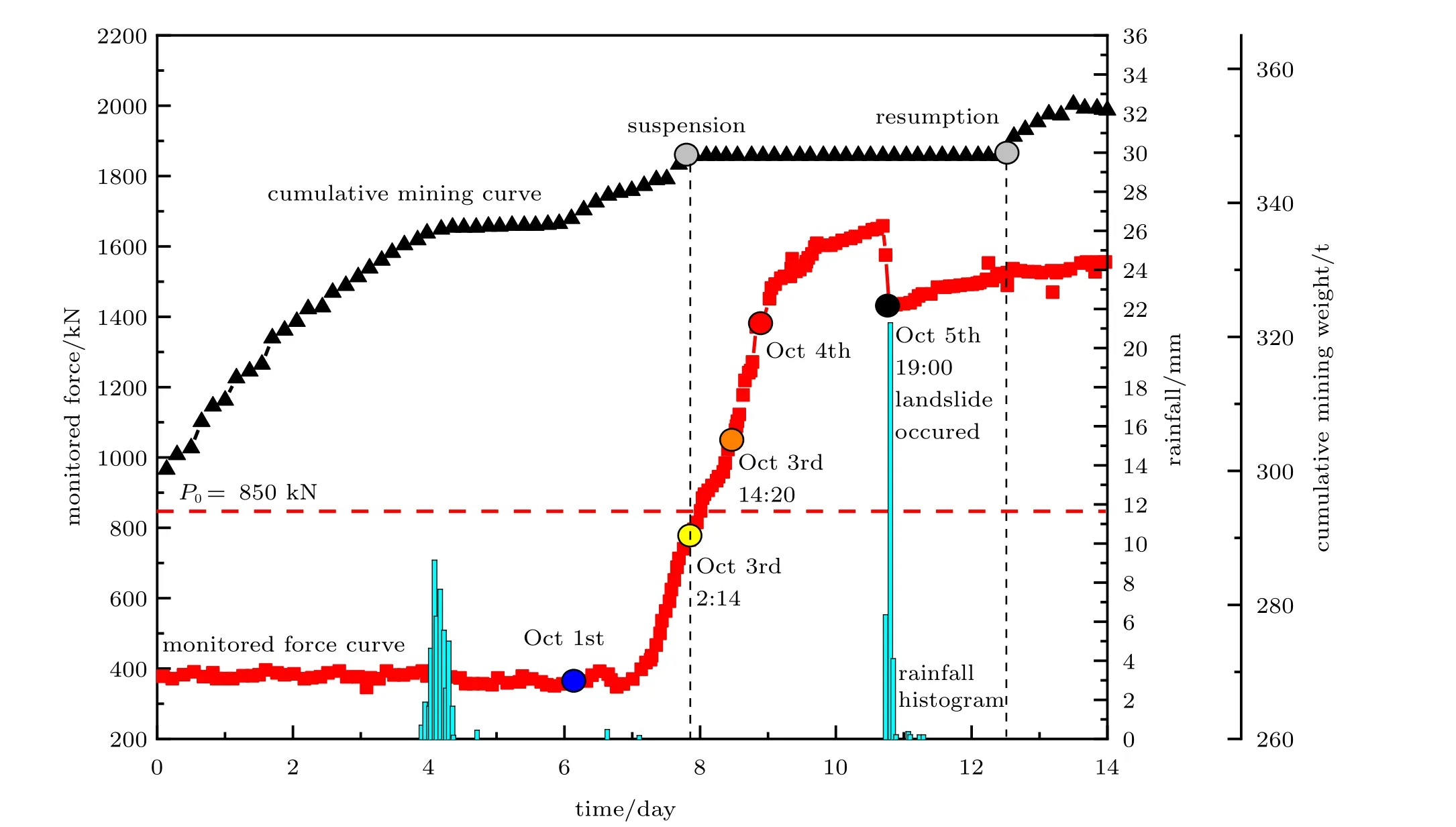
图17 下滑力降雨耦合监测曲线[23]Fig.17 Slippage force and rainfall coupling monitoring chart[23]
根据监测结果可知,监测力曲线开始上升之前有降雨情况,10 月5 日的降雨诱发了本次滑坡灾害,是其发生的必要条件,而只有当日出现的监测力突降说明了滑坡产生的直接原因,是滑坡灾害发生的充分必要条件。南芬露天铁矿NFMS 系统所用NPR锚索恒阻力平均值为850 kN,监测过程初期监测力曲线为380 kN 左右,说明NPR 锚索仅发生部分弹性变形。10 月3 日发出黄色预警后,监测力达到锚索恒阻值,开始输出结构变形。10 月5 日发生滑坡时,监测力降至1400 kN,仍高于锚索恒阻值,说明NPR 锚索仍在发挥正常锚固作用,在提供恒定工作阻力的同时实时监测滑坡体受力情况。
6 结论
NPR 锚杆/索具有拉不断、高恒阻力等力学特性,其恒阻力只与负泊松比结构的摩擦系数、材料参数IS和几何参数IC相关,与外载荷和岩石特性无关,其本构模型由弹性体与H-G 体串联而成,形成具有粘滑行为的本构关系;对于工程应用中的NPR锚杆/索,其刚度为小量且动、静摩擦系数十分接近,因此NPR 锚杆/索可以进一步简化为理想弹塑性本构关系。
NPR 锚杆/索支护的岩体形成了具有负泊松比支护效应的岩体,即NPR 岩体;将岩体流变模型与NPR 锚杆/索模型并联构成NPR 岩体本构模型,在静载作用下,表现出应力阶梯型下降的让压力学行为,可以实现NPR 锚杆力学行为与岩体力学行为的解耦分析,通过小扰动控制的方法,可以实现岩体的非线性力学行为的降维分析,将岩体的复杂非线性行为降维转化为确定性与可预测的力学行为。
NPR 锚杆/索在煤矿冲击地压、围岩大变形控制以及滑坡控制与预测等方面得到了广泛成功应用。特别是基于NPR 锚索滑坡坡面机械力(牛顿力) 监测的滑坡预测案例,充分证明了NPR 岩体具有的力学行为解耦分析与小扰动控制的超常特性。NPR 锚杆/索支护岩体相互作用理论的研究推动了矿山岩体力学的发展,其应用为解决深部开采中岩体复杂非线性行为认识和工程灾害预测提供了新的途径。
