悬浇拱桥索力设计计算分析
2022-09-28王玲丽陶鹏飞
王玲丽、陶鹏飞
(贵州省交通规划勘察设计研究院有限公司,贵州 贵阳550001)
0 引言
拱桥主拱圈线形为曲线,拱脚支撑处同时受竖向力、水平力作用,水平力既减小了拱桥跨中弯矩,又在拱内产生了轴向压力,提高了混凝土拱桥的承载力。拱桥跨度和施工方法紧密相关,200~300m 跨度的拱桥主要采用悬臂法施工,斜拉扣挂悬臂浇筑法是通过在交界墩上设置扣塔,利用扣锚索系统拉住拱圈悬臂浇筑节段,待合龙段混凝土浇筑后,逐步对称拆除扣锚索,再浇筑拱上垫梁、立柱、盖梁、上部结构、桥面系。
拱圈悬浇过程中,为保证混凝土拉应力不超限,须选择合适的扣锚索进行拆除,合龙段合龙后,逐步对称拆除余下全部扣锚索,因此,成桥后拱圈混凝土的受力状态不能通过调整扣锚索改善拉力,施工过程中扣锚索的初始张拉力对拱桥的受力影响较大。以主跨200m 悬浇拱桥为例,介绍悬浇拱桥扣锚索设计及初始索力的确定过程。
1 工程概况
娅石庆特大桥是贵州省金沙经仁怀至桐梓高速公路上的重要控制性工程,桥位地处乌蒙山与娄山山脉的交汇处,场区为深切“U 形”沟谷地形,沟谷宽约139m,深约115m,河两岸陡崖前缘均有卸荷裂隙带,卸荷裂隙走向基本与陡崖平行,垂直竖向发育,延伸较长。 梁基线通过地段的地面高程为865.9~1041.2m,相对高差175.3m。
综合考虑地形、地质、施工、造价等因素,全桥孔跨布置为:2×30 简支T 梁+200m(净跨径)钢筋混凝土箱型拱+6×30 先简支后结构连续预制T 梁,桥梁全长469.2m,全桥立面图如图1 所示。
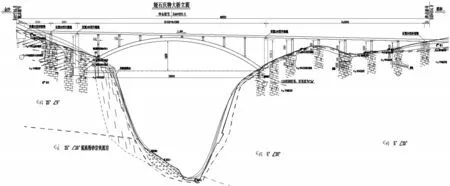
图1 全桥立面图
2 扣锚索设计计算
为保证施工过程中混凝土拉应力不超限以及成桥后线形,需对扣锚索及扣锚索的张拉过程进行设计,扣锚索及扣锚索的张拉过程设计包括:扣锚索张拉端位置的设计、扣锚索钢束根数的设计、各扣锚索张拉拆除顺序的设计、扣锚索张拉力的设计。
2.1 扣锚索张拉端位置的设计
根据扣锚索提供更大的竖向力、扣索倾角不小于10、扣塔的高度不至于太高的原则,确定0~16 号扣索在交界墩及扣塔上的张拉端位置,同时为平衡扣索产生的拉力,保证交界墩的稳定,设置与扣索相对应的锚索。扣锚索布置形式有星式布置、扇形布置两种,星式布置可以提供更大的竖向力,扇形布置方便布置扣锚索。该项目采用星式与扇形组合布置形式,全桥主拱圈共设置17 个节段,金沙岸、桐梓岸分别设置17 对扣锚索,0~6 号扣索采用星式布置,7~16 号扣索采用扇形布置。扣锚索张拉端布置形式如下:0~3 号节段扣锚索在交界墩中部操作平台的钢板上,4~6 号节段扣锚索在交界墩盖梁的锚箱上,7~16 号节段扣锚索在扣塔第一至四层的钢锚箱上。
2.2 扣锚索钢束根数设计
扣索主要用于承受悬浇节段重量及施工挂篮重量,根据悬浇节段重量、施工挂篮重量、扣索倾角,初步确定需要的扣索钢束根数。同时,为平衡扣索产生的水平力,根据锚索倾角,初步确定需要的锚索钢束根数。待求出索力后,反算出拉索面积及需要的钢束根数。
2.3 各扣锚索张拉拆除顺序的设计、扣锚索张拉力的设计
扣锚索张拉力的设计可参考斜拉桥索力的设计方法,斜拉桥索力优化包括两大类:恒载索力无约束优化法、有约束优化法,主要有简支梁法、零位移法、内力(或应力)平衡法、最小弯曲能法、可行域法等。该项目采用最小弯曲能法,将索力优化的目标条件设为施工过程中拱圈混凝土的拉应力不超限,且施工过程中拱圈线形与成桥线形接近,目标状态先选取最大悬臂状态下,再根据扣锚索张拉拆除顺序确定相应的目标状态。
最小弯曲能法可采用将主拱圈、交界墩的抗弯刚度缩小10以及将主拱圈、交界墩、扣锚索的截面面积放大10两种方式,设计中分别采用上述两种方式计算不拆除扣锚索最大悬臂状态下的扣锚索的内力,并将求得的结果对比。利用Midas 建立有限元模型,先采用将主拱圈、交界墩的抗弯刚度缩小10,令拉索的初始拉力为零,计算提取扣索内力;另建模型,将主拱圈、交界墩、扣锚索的截面面积放大10,令拉索的初始拉力为零,计算提取扣索内力,以上两种情况下索内力对比如图2 所示,通过对比图发现,缩小主拱圈、交界墩的抗弯刚度后计算出的扣索内力稍微规则一些,而放大主拱圈、交界墩、扣锚索的截面面积后计算出的扣索内力分布非常不规律,因此,该项目运用的最小弯曲能量法,均采用将主拱圈、交界墩的抗弯刚度缩小10;另外,从图中可以看出K0~K5 的扣索索力值普遍较小,且呈现明显不规律变化,说明索的布置需要调整。
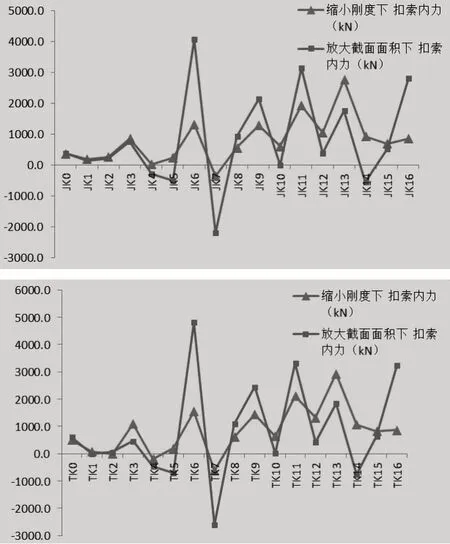
图2 扣锚索索力对比图
根据上述分析,将目标状态设为主拱圈施工至5号节段时0~5 号扣锚索拉住0~5 号主拱圈(状态一)、最大悬臂状态下6~16 号扣锚索拉住主拱圈(状态二),并采用最小弯曲能法分别计算两种状态下的扣锚索索力值,发现状态一下0~5 号扣锚索的索力值均为正值,且没有突然变小的现象。分别建立0~5号、0~6 号、0~7 号、0~8 号、0~9 号、0~10 号扣锚索拉住主拱圈模型,计算以上各种状态下的扣锚索索力值,发现0~10 号扣锚索拉住主拱圈时,7 号扣锚索索力值突然变小,因此在张拉10 号扣锚索时,需拆除某个扣锚索。为保证施工安全及主拱圈拉应力不超限,需分批次拆除0~6 号扣锚索,拟定张拉5 号扣锚索时拆除0 号扣锚索,张拉6 号扣锚索时拆除1 号扣锚索,张拉11 号扣锚索时拆除2 号扣锚索,制定扣锚索张拉拆除顺序如下:张拉0 号扣锚索—张拉1 号扣锚索—张拉2 号扣锚索—张拉3 号扣锚索—张拉4 号扣锚索—张拉5 号扣锚索、拆除0 号扣锚索—张拉6号扣锚索、拆除1 号扣锚索—张拉7 号扣锚索—张拉8号扣锚索—张拉9 号扣锚索—张拉10 号扣锚索—张拉11 号扣锚索、拆除2 号扣锚索—张拉12 号扣锚索、拆除3 号扣锚索—张拉13 号扣锚索、拆除4 号扣锚索—张拉14 号扣锚索、拆除5 号扣锚索—张拉15 号扣锚索—张拉16 号扣锚索—合龙段合龙后,依次对称拆除6、16 号扣锚索,再拆除7、15 号扣锚索,依次类推,共5~6 批分级卸载。合龙段合龙时全桥模型如图3所示。
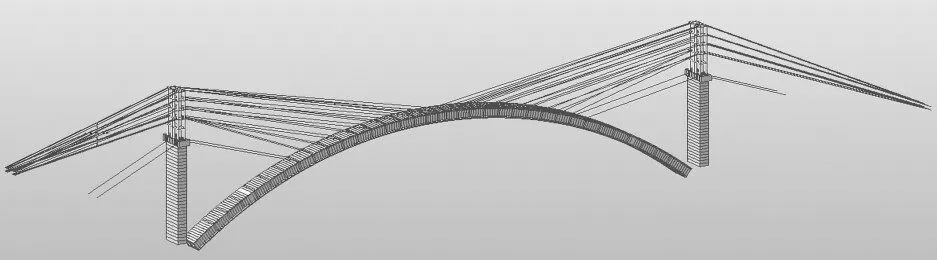
图3 合龙段合龙时全桥模型图
根据拟定的扣锚索张拉拆除顺序,利用最小弯曲能法或Midas 的未知荷载系数法,初步确定扣锚索初始拉力。目前扣锚索的张拉方式有两种,一种是一次张拉到位,施工过程中不再调整索力,另一种是先施加初始拉力,张拉其他节段扣锚索时再调整该索力。因拱圈节段较多,扣锚索数量较多,多次调整索力为施工带来不便。在200m 左右跨度拱桥中,多采用一次张拉到位,施工过程中不再调整索力的方法,该项目也采用一次张拉到位,施工过程中不调整索力的方法。分别采用上述两种方法计算扣锚索初始索力。
首先,采用最小弯曲能法计算各状态下的扣锚索内力值,建立0~5 号、1~5 号、2~6 号、3~11 号、4~12 号、5~13 号、6~14 号、6~16 号扣锚索拉住主拱圈状态模型,上述各状态的计算结果中,仍有个别扣锚索内力值为负,或突然变小情况,取各状态下的内力平均值的最大值作为扣锚索初始拉力。根据施工顺序建立含施工阶段的模型,将主拱圈、交界墩的抗弯刚度恢复正常后代入前述扣锚索索力,验算各施工阶段主拱圈混凝土的拉应力是否超限。通过计算发现,初始拉力下,大部分施工阶段的混凝土最大拉应力超限,需逐个阶段调整扣锚索拉力值,比如张拉1 号索力后混凝土最大拉应力超限,即需调整1 号索索力值,直至张拉1号索力后混凝土最大拉应力不超限,再查看张拉2 号索力后混凝土最大拉应力是否超限,如超限即调整2号索索力值,直至张拉2 号索力后混凝土最大拉应力不超限,依此类推,直至合龙段合龙,得到各扣锚索的拉力值。各扣锚索的初始拉力值如图4 所示。
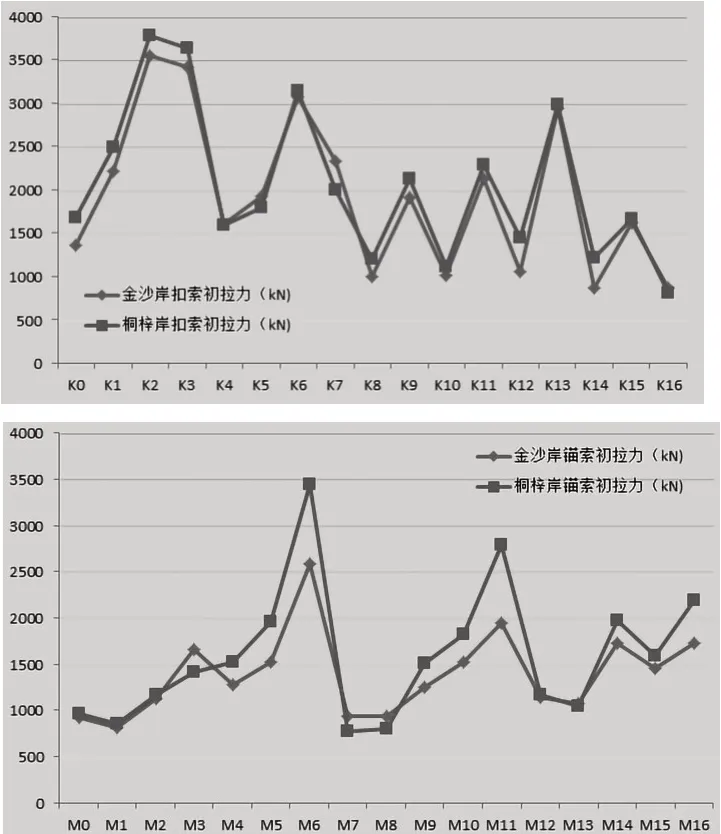
图4 采用最小弯曲能法计算的扣锚索初始索力图
为对比,再利用Midas 的未知荷载系数法,按拟定的施工顺序建立施工阶段模型,将拉索的初拉力设为100kN,以各施工阶段下各扣索拉住的箱梁节段的节点位移在±3mm 之间为控制目标,利用程序自带的未知荷载系数法计算出各扣锚索张拉拆除阶段的荷载系数,取各阶段荷载系数的最大值与100 的乘积作为扣锚索的初始张拉力。各扣锚索的初始拉力值如图5 所示。
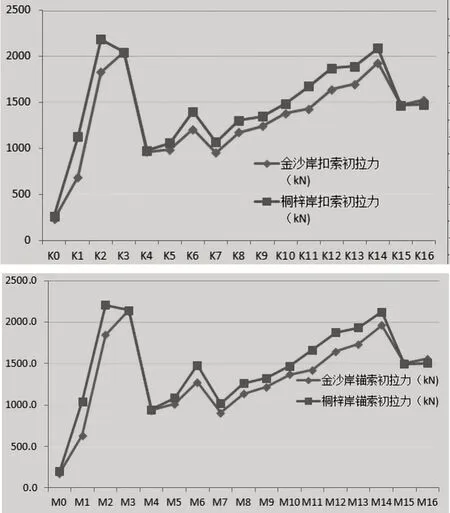
图5 采用未知荷载系数法计算的扣锚索初始索力图
扣锚索张拉过程中主拱圈的压应力储备较小,箱底出现拉应力。
3 结论
本文结合主跨200m 悬浇拱桥,介绍了悬浇拱桥扣锚索设计及初始索力的确定过程,并得出如下结论:
第一,悬浇拱桥的扣锚索张拉力设计可参考斜拉索索力的确定方法,但因悬浇拱桥的扣锚索为临时构件,拱圈合龙后所有扣锚索均需拆除,因此需首先确定扣锚索的张拉拆除顺序;
第二,最小弯曲能法计算悬浇拱桥的扣锚索初始索力时,采用缩小刚度的方法比采用放大截面面积法计算的索力均匀;
第三,拱桥悬浇过程中,扣锚索张拉过程中主拱圈的压应力储备较小,箱底出现拉应力。
