软弱岩土体中预应力锚索弯曲锚固段剪应力分析 *

叶 红，李 艳

(1. 武汉理工大学 土木工程与建筑学院，湖北 武汉 430070； 2. 武汉交通职业学院 交通工程学院，湖北 武汉 430065)

0 引 言

具有良好锚固效果的预应力锚索已被广泛地应用到边坡、基坑等的加固中[1]，而软弱岩土体由于其不连续性和各向异性，在外荷载作用下受荷区会发生弹性变形和塑性变形，即蠕变变形[2-3]，因此在预应力锚索长期加固的软弱岩土体中，岩土体由于预应力作用而发生蠕变，蠕变反过来又引起锚索预应力损失，锚索预应力与岩土体蠕变之间存在耦合效应关系。

由于软弱岩土体的复杂性，关于预应力锚索锚固机理还不清楚，业内学者正在进行深入的理论研究。王克忠等[4]、王国富等[5]、邓东平等[6]从锚索预应力与岩土体蠕变的耦合效应方面研究了预应力锚索的锚固机理；索玉文等[7]、于贵等[8-9]基于锚索锚固段弯曲采用半平面弹性理论研究了锚索锚固段的剪应力分布情况。针对软弱岩土体在外荷载作用下发生蠕变这个现象，笔者基于锚索预应力与软弱岩土体蠕变之间的耦合效应，结合Boussinesq-Flamant问题解和任意点的平面应力状态，对预应力锚索弯曲锚固段的切向剪应力进行了研究，得到弯曲锚固段切向剪应力的变化规律，研究结果补充完善了软弱岩土体中预应力锚索锚固机理。

1 耦合效应的特征方程

笔者采用一个Hooke体模型和一个Kelvin体模型串联而成的广义开尔文体(General Kelvin)模型来表征锚索的预应力和岩土体的蠕变，如图1。图中：EK、η分别为锚索周边岩土体的滞后弹性模量(单位：MPa)、黏性参数(单位：MPa·h)；EH为锚索的瞬时弹性模量(单位：MPa)；σ为锚索预应力与软弱岩土体蠕变耦合效应的计算应力(单位：MPa)[1]。

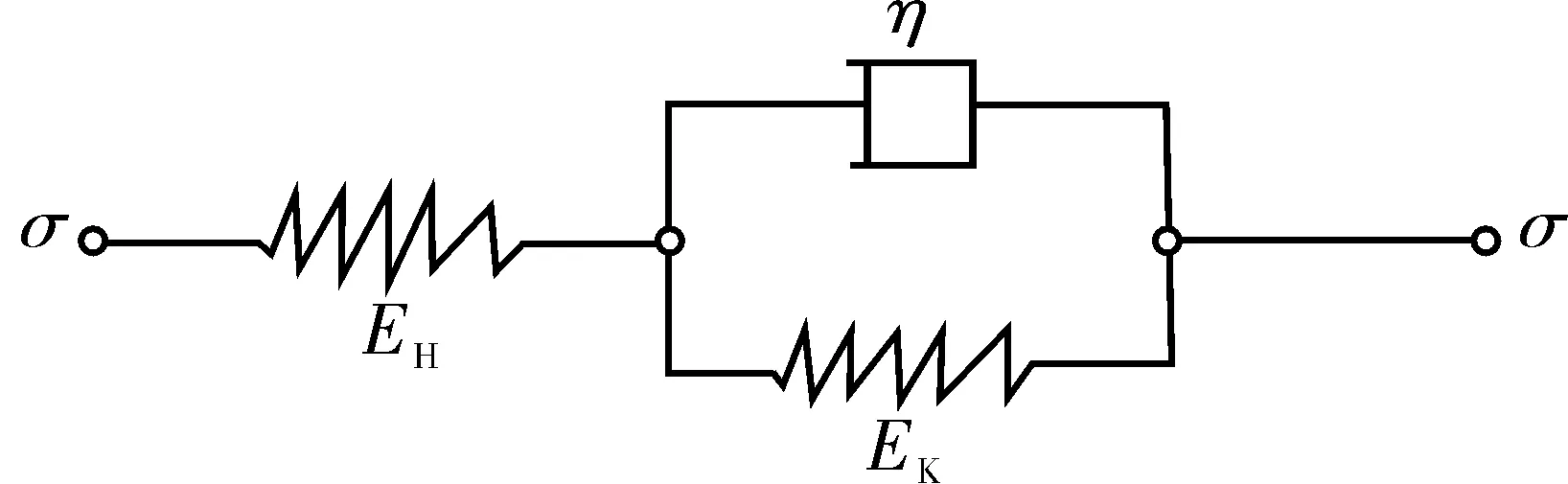
图1 广义开尔文模型Fig. 1 Model of general Kelvin

1.1 本构方程

General Kelvin模型的本构方程如式(1)：

(1)

式中：σK为General Kelvin模型锚索周边岩土体的应力，MPa；εK为General Kelvin模型锚索周边岩土体的应变；其他符号同前。

由图1的静力平衡条件可得

(2)

式中：ε为锚索预应力与软弱岩土体蠕变耦合效应计算模型的应变；σH为锚索的应力，MPa；εH为锚索的应变；其他符号同前。

将式(2)代入式(1)得到耦合效应计算模型的本构方程(3)：

(3)

1.2 松弛方程

在耦合效应计算模型的本构方程(3)中，如果锚索预应力变化而应变没有变化，此时ε为常数C，则有

(4)

已知初始条件下σt=0=EHC，由式(4)可得到耦合效应计算模型的松弛方程(5)：

(5)

锚索预应力荷载F(单位：kN)随时间t而逐渐减少，如式(6)：

(6)

式中：A为预应力锚索钢绞线的截面面积，m2；其他符号同前。

2 弯曲锚固段的剪应力

2.1 Boussinesq-Flamant问题解

通常，预应力锚索孔道采用潜孔钻施工方法来钻探，由于地质因素、技术因素和工艺因素等的影响，在钻进过程中孔道往往会发生弯曲而偏离设计要求[10]，尤其是在较长孔道的钻探施工过程中，锚索孔道会呈现向下弯曲的状态。一般来说，位于软弱岩土体中的锚索孔道越长，孔道向下弯曲的幅度也就越大[11]。

预应力锚索的钢绞线所受到的拉力传递到注浆体上后转化为剪应力和压应力，注浆体受到的剪应力的方向与钢绞线受到的拉力的方向相反[7]，并沿锚索孔圆心对称[12]。锚索孔道弯曲半径为R，预应力锚索孔道直径为D，若锚索锚固段弯曲处内曲线和外曲线不对称，则内曲线和外曲线上任意点的切向剪应力不相等[8-9]，如图2。

图2 锚索弯曲锚固段受力示意Fig. 2 Force diagram of bending anchorage section ofthe anchor cable

锚索预应力荷载F作用在软弱岩土体表面时，可由弹性力学理论Boussinesq-Flamant问题解得到预应力锚索锚固段应力的表达式[7-9]：

(7)

(8)

(9)

式中：σx、σy、τxy分别为直角坐标系下锚固段内、外曲线上任意点的应力，MPa；其他符号同前。

预应力锚索弯曲锚固段内曲线和外曲线的变化规律均与锚索孔道弯曲半径R和锚索孔道直径D存在数学函数关系，如图3。

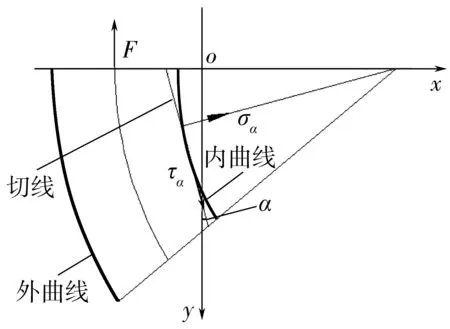
图3 锚索弯曲锚固段力学分析示意Fig. 3 Mechanical diagram of bending anchorage section ofthe anchor cable

因此，可得到在直角坐标系下弯曲锚固段内、外曲线的函数式fi(x,y)、fo(x,y)，分别代入式(7)～式(9)，可得到直角坐标系下预应力锚索锚固段内、外曲线上任意点的应力。

2.2 预应力锚索锚固段内、外曲线上任意点的平面应力状态

斜面应力公式或应力变换公式即柯西应力公式，是弹性力学中常用公式之一[13-14]。三维坐标下的柯西应力公式如式(10)：

tN=σ·N

(10)

对于平面应力问题，如果已知单元体上的应力(σx、σy、τyx)，可由柯西应力公式(10)得到斜面上的正向应力和切向应力[14]。在内曲线和外曲线确定的平面中，根据平面应力问题中任意点的应力状态(图4)，可由柯西应力公式(10)得到锚索锚固段内曲线或外曲线任意点的法向正应力和切向剪应力，如式(11)：

(11)

式中：σα、τα分别为锚索锚固段弯曲孔道内、外曲线上任意点的法向正应力和切向剪应力，MPa；α为锚索弯曲锚固段内、外曲线上任意点的切线与y轴之间的锐角，(°)。

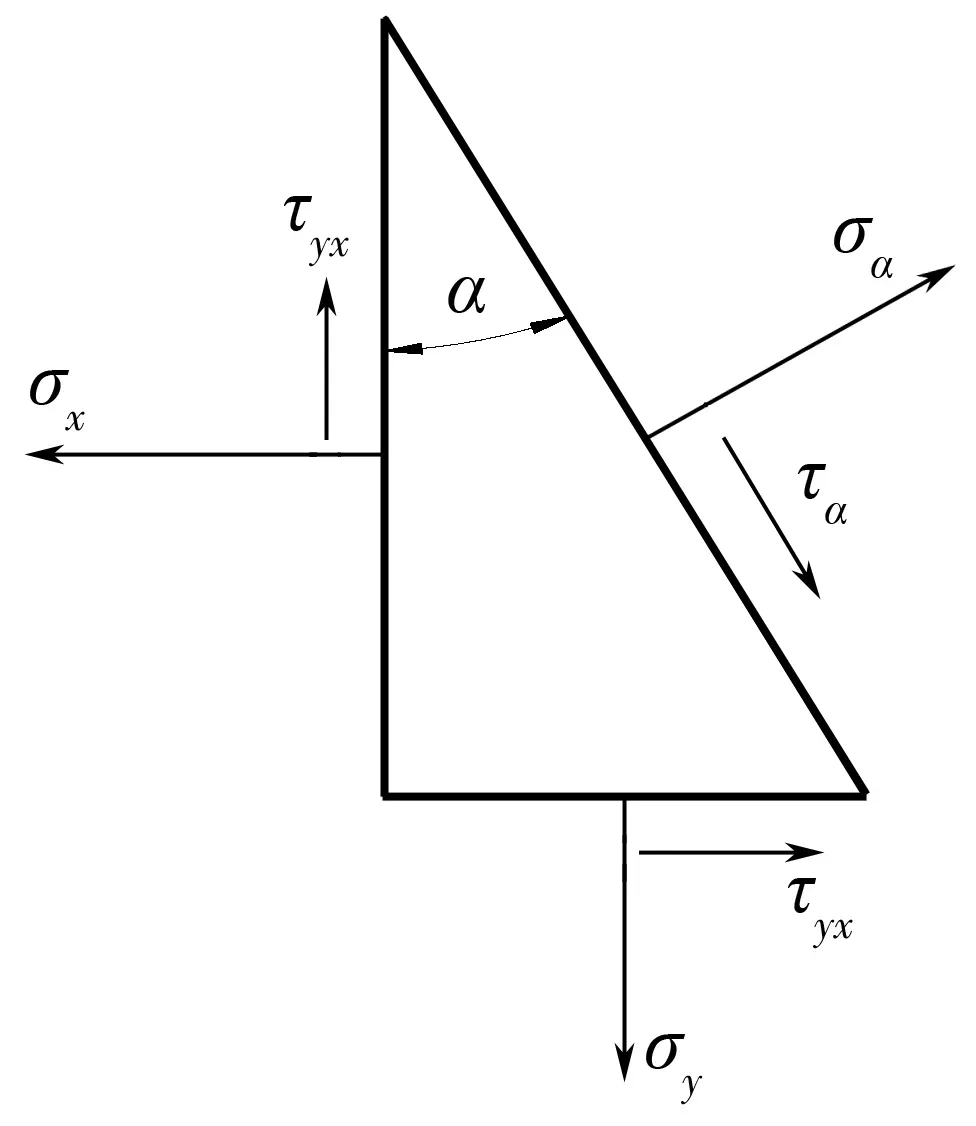
图4 平面应力状态应力分析示意Fig. 4 Stress analysis diagram of plane stress state

2.3 预应力锚索锚固段内、外曲线上任意点的切向剪应力

分别将内、外曲线函数fi(x,y)、fo(x,y)，及式(7)～式(9)代入式(11)，可得到预应力锚索弯曲锚固段内、外曲线上任意点的切向剪应力τi、τo：

(12)

(13)

3 算例分析

借鉴陈安敏等[15]、王国富等[16]的锚索蠕变相似试验研究成果，某经过预应力锚索加固的软弱岩土体边坡，假设软弱岩土体的瞬时弹性模量EH=9.362 MPa，滞后弹性模量EK=7.719 MPa，黏性参数η=607.795 MPa·h，C=9.53×10-5。预应力初始值F0=100 kN。如果预应力锚索锚固段长S=4.5 m，锚索孔直径D=0.14 m，经专用设备测试得锚索孔道弯曲半径R=10 m，则弯曲锚固段内、外曲线上任意点的切线锐角α由式(14)表示：

(14)

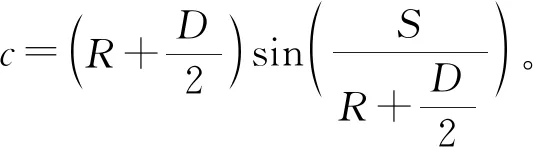
3.1 锚索预应力初始值F0的影响

如果锚索预应力初始值F0=100、200、400 kN，由图5可见，由于锚索预应力变化与软弱岩土体蠕变之间的耦合效应，从加载后开始计时，锚索预应力荷载F随着时间t的增加而按幂函数递减。

图5 锚索预应力随时间t的变化曲线Fig. 5 Variation curve of anchor cable prestress changing with time t

当F0=100、200、400 kN，t=480 h[15-16]时，预应力锚索弯曲锚固段内、外曲线切向剪应力分布如图6；预应力锚索弯曲锚固段内、外曲线切向剪应力峰值如表1。

图6 F0=100, 200, 400 kN,锚索弯曲锚固段内、外曲线切向剪应力分布曲线Fig. 6 Tangential shear stress distribution curve of the inner and outer curves of bending anchorage section of the anchor cable withF0=100, 200, 400 kN

表1 F0=100, 200, 400 kN，弯曲锚固段内、外曲线切向剪应力峰值Table 1 The peak value of tangential shear stress of the inner andouter curves of bending anchorage section of the anchor cable withF0=100, 200, 400 kNMPa

由图6、表1可知：

1)锚索弯曲锚固段，内、外曲线上任意点的切向剪应力分布曲线均随着F0的增加而逐渐陡峭，且内、外曲线上任意点的切向剪应力主要集中在锚头0.5 m范围内。

2)锚索弯曲锚固段，内、外曲线的切向剪应力峰值τi, peak、τo，peak均随着F0的增加而呈线性变化，且有τi,peak≈2.9τo,peak。

3.2 锚索孔道弯曲半径R的影响

当锚索弯曲锚固段孔道弯曲半径R=5、10、20 m时，锚索弯曲锚固段内、外曲线的切向剪应力分布曲线如图7，切向剪应力峰值如表2。

图7 R=5, 10, 20 m,锚索弯曲锚固段内、外曲线切向剪应力分布曲线Fig. 7 Tangential shear stress distribution curve of the inner andouter curves of bending anchorage section of the anchor cable withR=5, 10, 20 m

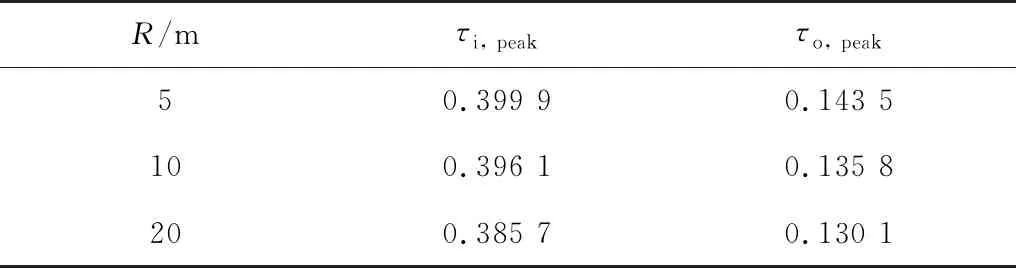
表2 R=5, 10, 20 m锚索弯曲锚固段内、外曲线切向剪应力峰值Table 2 The peak value of tangential shear stress of the inner andouter curves of bending anchorage section of the anchor cable withR=5, 10, 20 mMPa

由图7、表2可知：

1)锚索弯曲锚固段，内、外曲线的切向剪应力分布曲线随R的增加而逐渐平缓。

2)锚索弯曲锚固段，内、外曲线的切向剪应力峰值τi, peak、τo, peak均随R的增加而逐渐减小，且τi, peak>τo, peak。

4 结 论

基于锚索预应力变化与软弱岩土体蠕变之间的耦合效应，根据Boussinesq-Flamant问题解，对预应力锚索弯曲锚固段切向剪应力进行了理论推导；算例分析了锚索弯曲锚固段内、外曲线的切向剪应力，得到以下结论：

1)在预应力变化与岩土体蠕变的耦合效应下，锚索的预应力随着时间按幂函数递减。

2)锚索弯曲锚固段任意点的切向剪应力主要集中在锚头0.5 m范围内，且切向剪应力峰值与预应力初始值成正相关关系。

3)锚索弯曲锚固段，内曲线任意点的切向剪应力峰值比外曲线任意点的切向剪应力峰值大。

4)锚索弯曲锚固段，孔道弯曲半径与锚固段内、外曲线切向剪应力峰值之间存在负相关关系。