异形截面桩截面参数优化设计研究
2022-03-12杨宁杜帅
杨 宁 杜 帅
(滨州学院建筑工程学院,山东滨州 256600)
桩是将建筑物的载荷传递给地基土的传力构件,被广泛应用于高层建筑、港口、桥梁等工程中。改革开放以来,黄河三角洲经济快速发展,涌现出一批超高建筑,随着海上采油平台和外海开敞式码头的不断兴建,普通桩型难以同时满足安全性与经济性[1]。因此需要采用“异形截面桩”(简称异形桩)来提高承载力,降低材料用量。目前异形桩的设计还没有成熟的标准与规范,其力学性能的优化问题亟待解决。
针对异形桩的截面优化设计,已经有很多专家进行了相关研究。王新泉等[2]设计了反拱曲面X形新型异形桩,并得出了其侧摩阻力和端阻力产生附加应力系数与外包方形截面边长和开弧间距的关系。魏作安等[3]从力平衡的角度,分析了抗滑桩的抗滑阻力与滑体的下滑力之间的依存关系以及传递过程。祁生文等[4]对夯扩异形桩施工震动效应进行分析,发现了夯扩异形桩施工振动产生的质点振动参数与振源的关系。吕亚茹等[5]对异形桩桩土载荷传递机理理论进行了分析,通过平衡分析方法得到了考虑桩土剪切作用的单桩载荷传递计算方法,并初步探讨了异形桩的异形效应。孔纲强等[6]进行了极限载荷下纵向截面异形桩破坏形式对比模型试验研究,分析了各级载荷下桩端和桩侧土体位移场的变化规律以及极限载荷下的破坏形式。由此可见,目前开展的研究都只针对于某种特殊形式的异形桩,并没有给出更有普遍性的规律。
为实现对不同截面形状异形桩的优化设计,需要对影响其力学性能的重要结构参数进行归类分析,在探究其影响机理的基础上,得出不同结构参数改变时异形桩承载能力的变化趋势与最优解。根据目前存在的异形桩的特点可以发现,桩的横截面形状变化主要体现在截面边界凹凸性、外尖角个数、夹角等几何参数的不同,当截面形状发生改变时,桩周面积、桩顶面积、截面惯性矩等与桩体力学性能十分密切的参数均发生相应改变,进而影响异形桩的竖向承载力与抗弯性能。本文采用分离变量法对异形桩进行参数化分析,在特定截面周长、面积的情况下,改变异形桩横截面边数与夹角,探究不同截面参数对异形桩力学性能的影响,为解决异形桩优化设计问题提供理论依据。
1 异形桩截面参数化设计
1.1 异形桩截面参数的选取
目前工程中常见的混凝土桩基础种类繁多,即使同种类型的桩基础,针对于不同的工程条件,也会有多个截面参数发生变化,因此需要进行适当的简化处理。预制混凝土方桩是常见的一种多边形截面桩(见图1(a))[7],可以近似简化为正方形。一种Y型桩(见图1(b))[8]的横截面包括模板弧度、开弧间距、夹角度数等设计参数,可以近似简化为三个外尖角的内凹型截面。
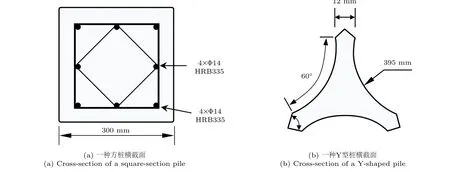
图1 部分桩基础横截面Fig.1 Cross-section of some piles
综合多种桩基础横截面形状特点,针对更具有普遍性的一般情况,避免截面各向异性带来的影响,将截面简化为中心对称图形,根据横截面几何形状是否含内凹尖角可以分为外凸型(见图2(a))和内凹型(见图2(b)) 两类。结合多种异形桩的特点,本文将截面关键参数限定如下两个:

图2 不同参数截面示意图Fig.2 Schematic diagram of cross-sections with different parameters
(1) 外尖角个数N,当N趋向无穷大时,截面为圆形;
(2) 外尖角夹角θ。
1.2 异形桩截面的参数化
桩在土体中承担竖向载荷时,其承载力主要通过桩周土体的侧阻力与桩低土体的支持力提供,当截面参数选取不同数值时,异形桩的桩身面积、桩周面积等几何参数都会随之改变,从而影响桩在工程应用时的力学性能。下面选取较为重要的几何参数进行分析。
(1) 桩身面积A身
对于外凸型截面,假设截面周长L为定值,将横截面分为关于中心对称的N个等腰三角形,取其中一份进行分析计算(见图3(a)),三角形顶角为2π/N,底边长为L/N,由此可得桩身横截面的总面积为

对于内凹型截面,将横截面分为关于中心对称的N个四边形,取其中一份进行分析计算(见图3(b)),可以分为两个等腰三角形,顶角分为别2π/N和θ,共用底边长为Lsin(θ/2)/N,由此可得桩身横截面总面积为

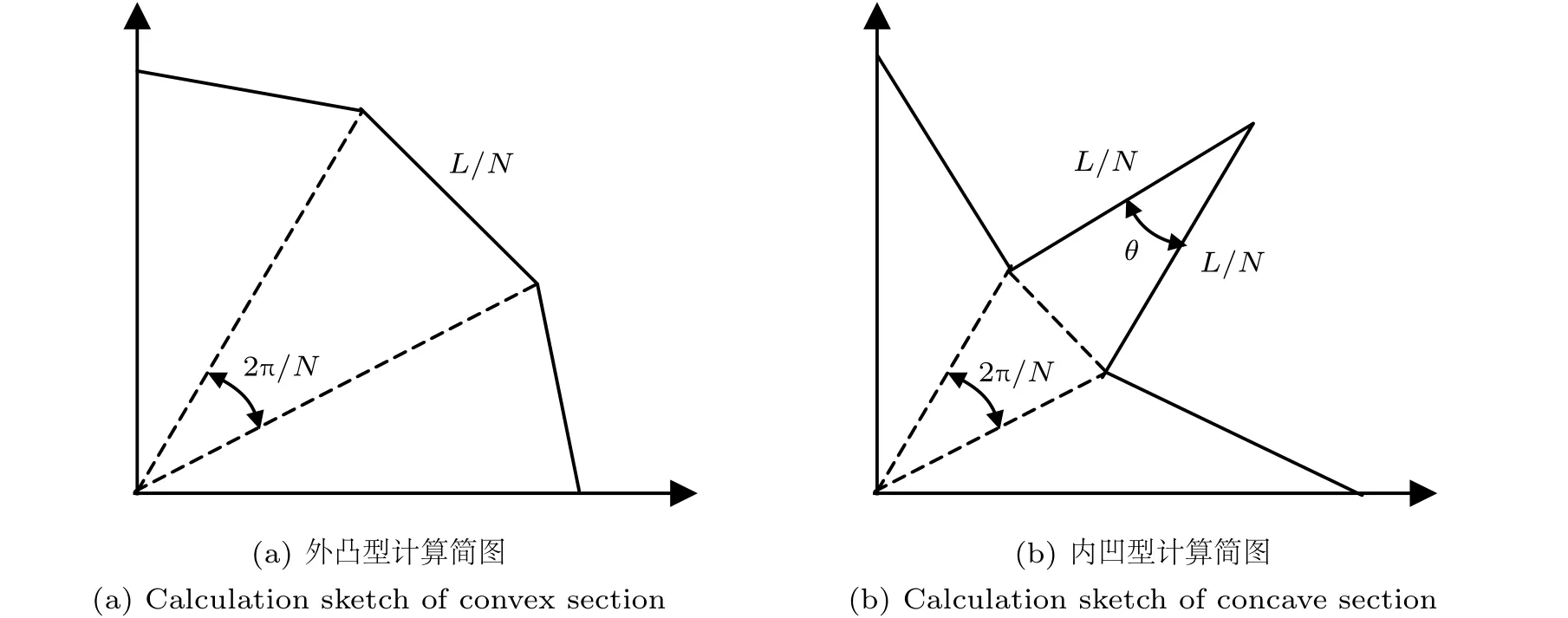
图3 固定周长时的桩身面积计算简图Fig.3 Calculation sketch of section area for fixed perimeter
(2) 桩侧面积A侧
对于等截面桩,其桩侧面积等于横截面周长L乘以桩长h,假设截面面积A身为定值,由式(1) 可得桩侧面积为

2 不同截面参数对异形桩力学性能的影响
2.1 桩侧面积不变时的桩身面积变化规律
在桩侧面积不变的情况下,假设桩横截面周长为定值,L分别取1000 mm,1200 mm,1400 mm,令N=3,4,...,10,计算外凸型和内凹型桩身面积随外尖角个数变化规律,如图4 和图5 所示。
对于外凸型截面,当截面周长不变时,桩身面积随外顶角个数N增大而增大,当N值较小时该变量对桩身面积有明显影响,当N值较大(如N>6)时桩身面积趋向于恒定极限值(见图4)。由式(1)可知,当N趋向于∞时,桩身面积极限值为圆形截面面积L2/(4π),该极限值即为相同周长的管桩横截面积,随截面周长L的增大而增大。
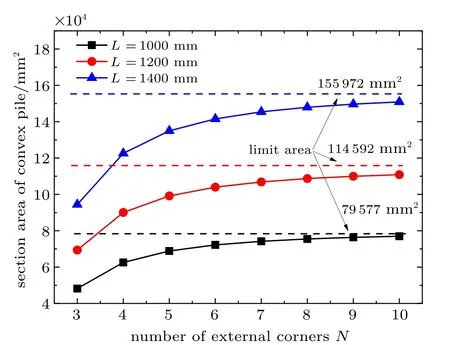
图4 不同截面周长的外凸型桩身面积随外尖角个数变化关系Fig.4 Section area with respect to the number of external corners for convex piles of different perimeter
对于内凹型截面,当截面周长不变时,桩身面积随外顶角个数N增大而呈下降趋势,且下降速度随N的增大而减小(见图5)。由式(2) 可知,当N趋向于∞时,桩身面积趋于恒定极限值L2sin2(θ/2)/(4π),该极限值随截面周长L和外尖角夹角θ的增大而增大,且明显小于管桩横截面积。

图5 不同截面周长的内凹型桩身面积随外尖角个数变化关系Fig.5 Section area with respect to the number of external corners for concave piles of different perimeter
2.2 桩身面积不变时的桩侧面积变化规律
在桩身面积A身不变的情况下,桩侧面积与截面周长成正比,截面周长即为单位长度(h=1)桩侧面积。分别取定值A身为0.08 m2,0.1 m2,0.12 m2,令N=3,4,...,10,计算单位长度外凸型和内凹型截面周长L随外尖角个数变化规律,如图6 和图7所示。

图6 不同面积的外凸型截面周长随外尖角个数变化关系Fig.6 Section perimeter with respect to the number of external corners for convex piles of different area

对于内凹型截面,当桩身面积不变时,桩侧面积随外顶角个数N增大而呈上升趋势,且上升速度随N的增大而减小(见图7)。由式(4) 可知,当N趋向于∞时,桩身面积趋于无穷大,而非恒定值。考虑到实际情况,若N值足够大时,横截面外周单个边长极小,考虑实际混凝土材料的制作情况,取单个边长极小值为L/(2N) = 100 mm,则各曲线位于L>200N处为有效部分,曲线与直线L=200N相交处L取到最大值。
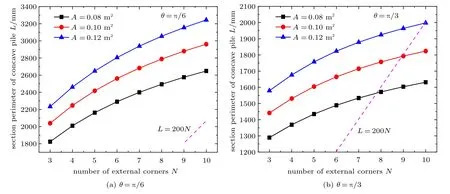
图7 不同面积的内凹型截面周长随外尖角个数变化关系Fig.7 Section perimeter with respect to the number of external corners for concave piles of different area
3 异形桩力学性能变化规律
3.1 异形桩竖向承载力变化规律
单根桩的竖向承载力由桩土相互作用力提供,与桩身面积、 桩侧面积等几何参数有关, 根据GB50007-2017 建筑地基基础设计规范[9],其计算公式为

式中Ra为单根桩竖向承载力特征值(kN),qsia为桩侧土体侧阻力特征值(kPa),qpa为持力层端阻力极限特征值(kPa)。
假设桩侧面与土体接触的有效长度为h,则相应的外凸型桩与内凹型桩竖向承载力分别为

单根桩基础所用混凝土、钢筋等材料总量与其体积成正比,所以体积越大则制造成本越高,为在控制制造成本的情况下获得最高的承载力,需要计算单位体积桩提供的承载力,计算公式为

假设桩长h= 10 m,土体为一般黏性土,端阻力特征值为qpa= 500 kPa,侧阻力特征值为qsia= 20 kPa,计算可得单位体积桩提供承载力变化规律(见图8)。内凹型异形桩与外凸型异形桩体现出不同的规律,单位体积内凹型异形桩提供承载力随外尖角个数N的增大而增大,单位体积外凸型异形桩提供承载力则随外尖角个数N的增大而减小。相同外尖角个数的情况下,单位体积内凹型异形桩提供承载力整体大于外凸型截面,且两者都随桩身面积的增大而减小。

图8 单位体积桩提供承载力变化规律Fig.8 Variation of bearing capacity provided by unit volume pile
由此可见,对于单位体积桩提供的承载力,内凹型异形桩整体优于外凸型异形桩。对于内凹型异形桩,单位体积桩承载力随横截面积A身的增大而减小,随外尖角个数N的增大而增大,即小截面、多尖角的内凹型异形桩在体积不变的情况下承载力更大。对于外凸型异形桩,单位体积桩承载力随截面积A身的增大而减小,随外尖角个数N的增大而减小,最小极限值为圆形截面桩(即管桩) 的承载力,即小截面、少尖角的外凸型异形桩在体积不变的情况下承载力更大。
单位体积桩提供的承载力随外尖角个数的变化规律,与截面周长随外尖角个数的变化规律呈现类似特征,说明桩侧面积与桩侧土体的摩擦阻力是影响单位体积桩承载力的主要因素。在异形桩的设计过程中,应重点考虑通过不同手段增加桩身侧面与土体的相互作用力,可以有效提升桩的竖向承载力。
3.2 异形桩抗弯性能变化规律
预制桩在运输、起吊过程中主要受到横向载荷产生弯曲变形,因此异型截面桩的抗弯性能也是重要的力学参数。假设异形桩所用材料相同,则其抗弯刚度则仅与截面惯性矩I有关。
根据杆件横截面的几何性质[10]可知,通过截面对称轴的坐标轴为形心主惯性轴,截面相对于该轴的惯性矩即为截面的形心主惯性矩,而由于上述简化图形既是轴对称图形又是中心对称图形,则选取不同对称轴对计算惯性矩没有影响。下面分别取定值A为0.08 m2,0.1 m2,0.12 m2,令N=3,4,...,10,通过AutoCAD 软件计算外凸型和内凹型截面对经过外尖角的对称轴计算形心主惯性矩I,(见图9),分析其抗弯性能随外尖角个数变化规律。

图9 截面惯性矩变化规律Fig.9 Variation of cross-sectional moment of inertia
由图9 可见,对于内凹型异形桩和外凸型异形桩,桩截面惯性矩I随截面积A的增大而增大,随外尖角个数N的增大而减小,即大截面、少尖角的外凸型异形桩在面积不变的情况下抗弯性能更好。
当外尖角个数N< 5 时,外凸型异形桩的截面惯性矩I减小较为明显,当N> 5 时,外凸型截面逐渐接近圆形截面,其惯性矩也越来越接近圆形截面(即管桩) 的惯性矩。而内凹型截面的惯性矩的下降速度也有逐渐放缓的趋势,对于同样截面面积异形桩的惯性矩,内凹型异形桩的抗弯性能稍大于外凸型异形桩。
4 结论
经过对内凹型和外凸型异形桩进行参数化分析,得出如下结论。
(1)对于外凸型截面,桩身面积随外顶角个数N增大而增大,桩侧面积随外顶角个数N增大而减小,外顶角个数越多越接近于管桩;对于内凹型截面,桩身面积随外顶角个数N增大而呈下降趋势,趋于恒定极限值,桩侧面积随外顶角个数N增大而呈上升趋势,考虑实际单个边长限制,桩侧面积最大值随桩身面积增大而增大。
(2)单位体积截面桩承载力随外尖角个数的变化规律,与截面周长随外尖角个数的变化规律呈现类似特征,说明桩与土体的侧摩擦阻力是影响承载力的主要因素,故在设计异形桩时,应通过不同手段增加桩身侧面与土体的相互作用力。
(3)内凹型异形桩的竖向承载能力与横向抗弯能力都优于同样截面面积的外凸型异形桩,且两种异形桩都优于管桩。内凹型异形桩可以增加外尖角个数来提升竖向承载力,但需要同时考虑因此带来的抗弯能力减弱;外凸型异形桩应尽量减少外尖角个数,以获得更高的竖向承载力和抗弯能力。
