倒指数形复合变幅杆的设计＊

巩建辉

（商洛职业技术学院机电工程系，陕西 商洛726000）

1 引言

超声变幅杆，也称超声变速杆或超声聚能器，是超声波振动系统中一个重要的组成部分。其主要作用是将振动系统中振动质点的位移和速度放大，同时也有改善换能器与辐射介质或超声波工具头之间的阻抗匹配作用，通过阻抗匹配，能有效的提高电声转化效率，降低超声波换能器的发热量。随着声学技术的发展，超声振动系统被广泛应用于医学、军事、工业、农业等多个领域[1]，超声变幅杆作为超声波振动系统中重要的组成部分自然成为国内外学者关注研究的热点，从纵振到扭转振动，从单一到复合，对新型变幅杆的设计研究从未停止。但总体来说对于超声变幅杆的位移和速度放大作用研究的较多，而对变幅杆的阻抗匹配作用研究较少[2-4]。为此这里提出一种倒指数形复合变幅杆，通过增大辐射的面积来改善换能器与介质之间的阻抗匹配，可提高换能器向液体辐射的声能，首先构建了倒指数形复合变幅杆的模型，然后利用变截面的波动方程得出各段的位移和频率方程，并求出变幅杆的谐振长度和放大系数等重要参数，最后用有限元软件ANSYS对其进行模态分析和谐响应分析，结果与理论值相吻合，此研究对起匹配作用的变幅杆的设计有一定的参考价值。

2 倒指数形复合变幅杆的设计

2.1 变幅杆的构建

该变幅杆是由一段四分之一波长的指数形杆和另一段四分之一波长圆柱杆组合而成，如图1所示，圆柱杆Ⅰ的长度、横截面直径和横截面积分别为l1，D1，S1，指数形杆Ⅱ的长度为l2，大小端圆形横截面直径分别为D2，D3，大小端横截面积分别为S2，S3。

2.2 变幅杆的设计理论

变截面杆在简谐振动情况下，其纵振动的波动方程为(1)式所示[5]

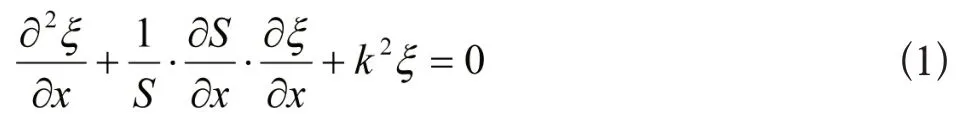
其中ξ 为复合变幅杆中质点的位移，k为圆波数，k=ω/c，ω为圆频率，为纵波在细杆中的传播速度。

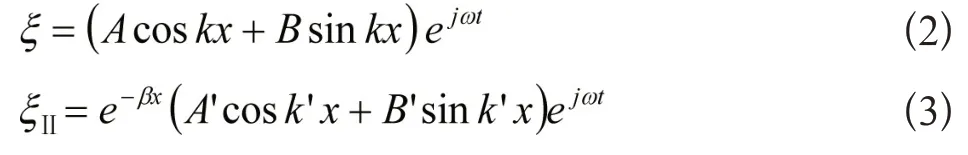
其中k'=是指数杆中纵波的波数，β=lnD3/D2，A，B，A'，B'为待定常数。

对于四分之一波长圆柱杆其左右边界条件分别为

将(2)式分别带入(4)式和(5)式进行分析可求得圆柱杆的共振频率方程为

对于四分之一波长指数杆其左右边界条件分别为

将(3)式分别带入(7)式和(8)式进行分析可求得圆柱杆的共振频率方程为

将(6)式和(9)式组合即可得到复合变幅杆的频率公式为

下面来解算倒指数形复合变幅杆的放大系数，设变幅杆左右端面处的位移分别为ξ1和ξ2，则由(2)式以及边界条件和式可得

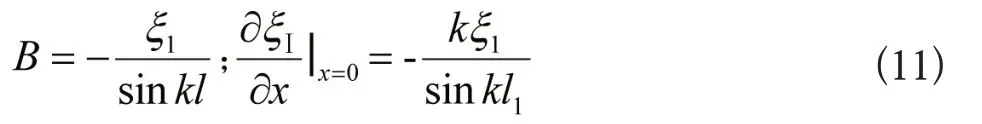
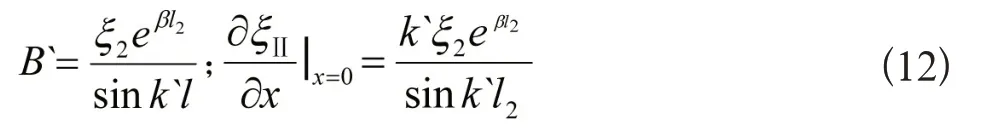
因为在x=0处力是连续的，所以由(10)、(11)和(12)式可得放大系数

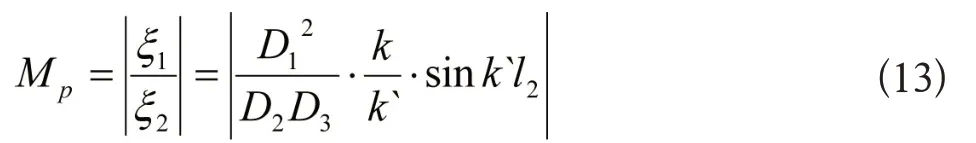
3 有限元分析

此复合型变幅杆的设计频率f=21kHz，纵波在细杆中的声速c=5．2×106mm/s，圆柱杆的截面直径D1=30mm，倒指数杆小端的截面直径D2=16mm，大端截面半径D3=40mm，利用Matlab对频率方程求数值解得到复合变幅杆的谐振长度l=98．3mm[6-8]，其中圆柱杆长度l1=59．1mm，指数杆长度l2=39．2mm。

采用ANSYS 软件对设计好的变幅杆进行模态分析和谐响应分析。首先进行模态分析，建立模型，定义单元类型，定义材料属性，建立几何模型和划分有限元网格；进行模态设置，进行模态扩展设置并求解。这里变幅杆的材料采用45 号钢，选用SOLID95 单元，采用自由网格划分，材料参数定义为弹性模量EX=210．9GPa，泊松比为PRXY=0．28，密度ρ=7800kg/m3。网格的划分情况如图2所示，运用分块兰索法(Block Lanczos)分析，模态提取频率范围为15kHz—30kHz，使用Solve 求解后得到其纵向振动的位移云图和沿轴向的位移曲线分别如图3、图4所示。

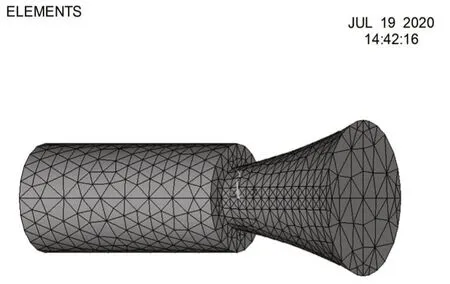
图2 变幅杆的有限元模型

图3 变幅杆的位移云图

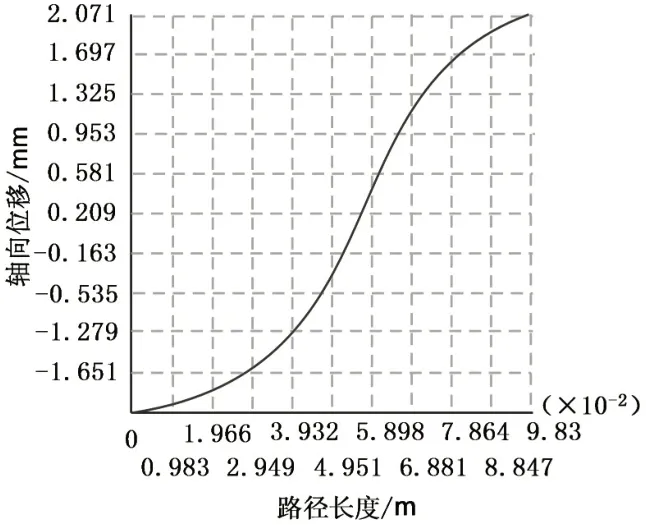
图4 变幅杆的轴向位移曲线

从云图上可以看出，当变幅杆时候发生纵振时频率f=20547Hz，节点的位置在四分之一波长的指数杆和四分之一波长的圆柱杆的交界面上，这和理论设计基本吻合。从轴向位移图可以看出变幅杆的放大倍数为1．25倍，放大倍数不大，这也是此变幅杆的特点，就是通过增大辐射面积来改善与液体等介质之间的阻抗匹配，即就是牺牲放大倍数来提高能量的传递效率。

在模态分析的基础上，然后进行谐响应分析，采用完全法(full)，这种方法是运用完整的系统矩阵来计算响应的[9-10]。在圆柱杆的左端面加载正弦变化的周期载荷，在变幅杆的输出端即指数杆的大端面输出的谐响应曲线如图5所示。从响应曲线可以看出在谐振频率大约20547Hz附近出现了振幅最大值，这与理论设计基本一致。

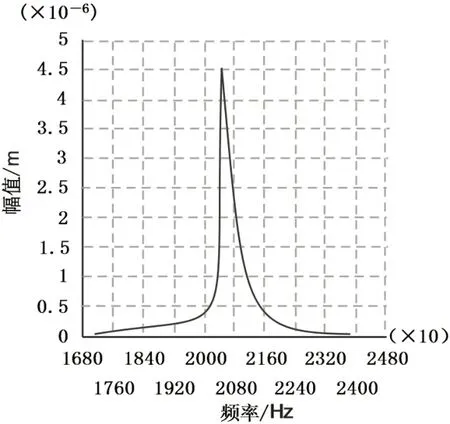
图5 谐响应曲线

4 结束语

构建了新型的倒指数形复合变幅杆的模型，利用变幅杆的设计理论得到了该新型变幅杆的频率方程。运用MATLAB软件解算频率方程得出了变幅杆的谐振长度，并借助于ANSYS 有限元分析软件对复合变幅杆进行了模态分析和谐响应分析，得出了变幅杆的纵振固有频率和理论相差2．1%符合设计要求，放大倍数为1．25倍比一般的变幅杆要低，但是却增大了输出面积更易于实现阻抗匹配便于能量的传输，充分体现了此变幅杆的主要特点。同时也进一步表明了将MATLAB 软件和ANSYS有限元分析软件配合使用对变幅杆的设计有一定的优势，MATLAB软件用于理论计算，ANSYS软件进行有限元仿真分析，两个配合使用可以提高变幅杆设计的效率。此研究可以作为其它变幅杆设计的参考，有一定的实际意义。