基于限幅模糊PID算法的果酒温度控制系统＊

张堂玉,龙祖强

(衡阳师范学院物理与电子工程学院，湖南 衡阳 421008)

1 引言

温度是影响果酒发酵品质的重要因素。传统温度接触器具有响应速度慢、控温精度低等特点，而智能模糊算法控制温度具有响应速度快、稳态性能好等优点，因而模糊算法是果酒发酵温度控制系统中的较优选择。

果酒发酵控制的主要任务是对发酵罐内的温度控制。针对果酒发酵温度控制系统存在大惯性和纯滞后等特点，研究者们提出了不同的算法来解决相应的问题。方良材等将PID 算法和模糊PID 算法分别应用于果酒发酵温度控制系统中[1-2]。由于温控对象通常具有大惯性和纯滞后等特点，采用传统PID算法难以达到理想效果，于是提出了将模糊算法和PID算法相结合的控制方法来减少系统的调节时间。吕宁等在模糊PID算法的基础上加入了变论域的思想，实现动态调整模糊控制器的论域范围以减少系统的超调量[3]。杨娜等针对传统PID 控制需要操作人员反复调整参数的问题，提出双模糊PID 控制分别对偏差进行精调和粗调以实现参数自动整定并提高了控制系统的稳态精度[4]。高锦等针对温控对象具有纯滞后的特点，提出了Smith 预估以解决温控系统的滞后问题[5]。上述研究都取得了较佳的控制效果，研究者们从“将不同的控制算法相结合”到“改变论域”等着力点去改善系统的性能。基于此，本文从“量化因子”出发，提出了一种限幅模糊PID算法。该算法与传统模糊算法的不同之处在于量化因子模块不再是一个线性函数，而是一个反正切非线性函数，以实现对果酒温度的精准快速控制。

2 系统总体设计

本文果酒发酵温度控制系统的期望值设定为30℃，系统总体设计框图如图1所示。将温度传感器采集到的温度通过A/D转换后送到控制系统中并与期望值进行比较。当采集到发酵罐内的温度比期望值高时，会得到一个反向误差值e。将误差值e通过模糊化、模糊推理、去模糊化处理后输出一个精确值u，然后通过D/A 转换后输出模拟信号用于加大电磁阀的开启度，以加快流入发酵罐外壁的冷水流量从而使温度降到期望值。当采集到发酵罐内的温度比期望值低时，此时会得到一个正向误差值e。同样将误差值e通过模糊化、模糊推理、去模糊化处理后输出一个精确值u，再通过D/A 转换后输出模拟信号用于减小电磁阀的开启度，以减少流入发酵罐外壁的冷水流量从而使温度升到期望值。

图1 系统总体设计框图

3 量化因子的设计

量化因子的选择需要满足对误差收敛的快速性和对误差变化率收敛的稳定性。误差收敛的快速性减少了系统的调节时间，误差变化率收敛的稳定性抑制了误差的变化状态从而提高了系统的稳态精度。因此本文选择满足这两者特性的arctan x 函数作为量化因子，下面将对arctan x函数的性能进行具体分析。

3.1 误差和误差变化率的收敛性

已知有公式可证明：

因此，我们可知arctan x在定义域中是收敛的，将它作为量化因子可对误差和误差变化率进行限幅。误差和误差变化率的模糊论域分别被限制在[0，1．6]和[-0．7，0]之间，限幅后的误差和误差变化率的波形如图2、3所示。

图2 限幅后误差波形图

图3 限幅后误差变化率波形图

3.2 误差收敛的快速性和误差变化率收敛的稳定性

令f(x)=arctanx，其中：函数的定义域为全体实数集R，值域为。函数与其导数的图像分别如图4、5所示。由上式可知：

图4 反正切函数图像

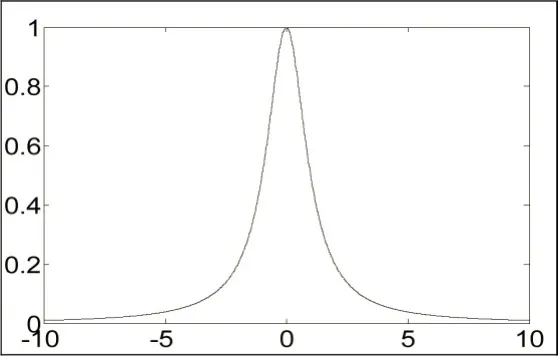
图5 反正切函数导数图像

由式(2)可知f'(x)≥0在定义域内恒成立。当且仅当x=0时，f'(x)=1成立。因此arctan x在定义域中是一个单调递增的奇函数。

量化因子是影响模糊控制器输出性能的重要因素。增大Ke可以提高控制误差的灵敏度以实现对误差收敛的快速性，但Ke过大会增加系统的调节时间，而Ke过小会降低系统的稳态精度；增大Kec可以降低误差的变化率从而提高系统的动态性能，但Kec过大会增加系统的过渡时间，而Kec过小会使系统产生超调和震荡。因此我们需要在一定的范围内增大Ke和Kec，从而保证误差收敛的快速性和误差变化率收敛的稳定性。令Ke=Kec=arctanx。在误差和误差变化率的模糊论域[0，1．6]和[-0．7，0]之间(即在一定的范围内)，arctan x单调递增的特性加快了误差收敛的速度并且也降低了误差的变化率从而保证了系统收敛的快速稳定性。

4 限幅模糊PID算法

本文针对果酒发酵温度控制系统，提出一种限幅模糊PID 控制算法。该算法是在传统模糊PID 算法的基础上引入反正切函数以减小误差和误差变化率的基本论域，使系统能快速稳定地消除偏差以达到温度期望值。针对温度控制系统存在纯滞后的问题，本文采用Smith预估实现非线性延时的补偿。Smith预估补偿的原理是通过引入一个和被控对象并联的补偿器对系统延时进行补偿和消除。

量化因子将误差和误差变化率的基本论域映射到模糊论域后进行模糊化、模糊推理和去模糊处理后将Kp、Ki和Kd输出至PID控制器[6]。限幅模糊PID系统框图如图6所示。

图6 限幅模糊PID系统框图

本文设计的模糊控制器采用双输入三输出结构，首先将温度误差e和误差变化率ec作为模糊控制器的输入，再通过模糊化、模糊推理、去模糊化得到三个精确输出值。

(1)模糊化

给定温度期望值为30℃，取量化因子Ke=Kec=arctan x，量化因子将误差e和误差变化率ec的模糊论域分别限制在[0，1．6]、[-0．7，0]之间。取比例因子K1=0．2，K2=0．004，K3=6，输出ΔKp、ΔKi、ΔKd的模糊论域分别都为[-1，+1]。各变量的模糊子集分别都为{NB，NM，NS，ZO，PS，PM，PB}。通过经验试凑法得到PID控制器的初值分别为6、0．004、40。

(2)模糊推理及模糊规则

本文采用Mamdani合成推理法，推理出如下规则：当|e|较大时，Kp取较大值，Kd取较小值，令Ki为0；当|e|、|ec|处于中等值时，Kp取较小值，Ki和Kd应取适中的值；当|e|较小时，增大Ki 和Kd 的值；当|ec|较小时，增大Kd的值；当|ec|较大时，减小Kd的值。

(3)去模糊化

去模糊化是指通过模糊推理后产生的输出模糊集合转换为精确输出值的方法。本文采用加权平均法进行去模糊化：

限幅模糊PID规则表如表1。

表1 限幅模糊PID规则表

由公式(3)计算出u(t)，其中ui和ωi分别表示第i条规则输出的结果和在总输出中所占分类的权重。

5 实验仿真

结合实践经验，果酒发酵温度控制系统的被控制对象传递函数可以表示为[7-8]

其中K表示放大倍数，T1表示惯性时间常数，表示滞后时间。将参数K=6．51，=48，T1=1325代入(5)式，可得

限幅模糊PID 系统仿真模型如图7所示。其中期望温度值由一个阶跃模块实现，目标温度设为30℃，在0时刻发生阶跃跳变。反正切函数模块作为量化因子以对误差和误差变化率进行限幅。子系统模块内部是由传统模糊PID 系统封装而成的。Smith预估补偿模块是由传递函数子模块、延时子模块和sum子模块组成，其原理是通过引入一个和被控对象并联的Smith预估补偿器对系统的纯滞后进行补偿和消除。

图7 限幅模糊PID系统仿真模型

同一受控对象，本文分别使用传统模糊PID 算法和限幅模糊PID 算法进行仿真对比。在限幅模糊PID 算法下，arctan x 对误差具有快速收敛性的同时也降低了误差的变化率，保证了系统收敛的稳定性。Smith预估控制可以对系统的滞后进行预估补偿，使系统能快速达到最佳状态。在两种算法下，得到实验结果如图8和表2所示。

表2 两种控制方法结果对比

图8 两种控制方法效果对比

6 结束语

在传统模糊PID 算法的基础上，本文通过引入反正切函数作为量化因子，对误差和误差变化率进行限幅。对误差和误差变化率，反正切函数具有快速稳定的收敛性，使得系统能快速消除偏差以达到温度期望值。采用Smith 预估补偿温控对象的延时解决了温度系统的滞后问题。仿真实验表明，限幅模糊PID 算法的调节时间比传统模糊PID算法的调节时间更短，性能更佳。因此，本文的限幅模糊PID算法对于工业上的温度控制系统具有很好的应用价值。