双层振动筛自动筛分最优振幅控制研究

涂晓琴,吴泽洲,李万权

（三川德青科技有限公司，湖北 武汉430000）

1 引言

自动筛分技术在冶金、煤炭等方面应用较为广泛。不仅可以提高生产效率，还能改善工艺效果，节约能源，在一定程度上能提高企业效益。筛分结果的好坏对下一步工作效率以及商品价值都会产生一定影响。在我国大约每年经过筛分的煤炭就有数十亿吨，因此改善筛分性能，提高筛分效率对经济发展具有十分重要的意义。

李丹菁等人提出不确定性通量筛分系统双子代数控制方法。在区间双子代数基础上，将输出反馈结果拓展到筛分系统中，对其自动优化生产进行控制；将输出结果和补偿项相结合，改进后的控制结构避免了对性能指标的限制，提高筛分效率[1]。曹培等人设计了筛分设备伺服控制系统。构建张弛筛力学模型与振动方程，获得张弛筛框与浮动筛框的振幅及相位关系；采用交叉耦合的转速控制手段与改进的Bang-Bang 的相位补偿算法实现对振幅的控制。仿真实验证明该方法调整时间快，超调量较小[2]。Haishen Jiang等人提出了一种新型变幅等厚弹性筛网(VAETES)，解决了蒸汽湿煤筛分过程中物料堆积和筛孔堵塞的问题。采用模拟和高速动态摄影技术，研究了瓦斯抽放过程中筛面和湿煤的运动学特性[3]。Ramatsetse 等人旨在以经济高效的方式将客户所需的各种尺寸和体积的矿物颗粒进行筛分。以确保RVS机器在采矿业使用时的最佳功能、可靠性和维护能力[4]。

上述几种传统方法虽然在一定程度上提高了筛分效率，但不能保证控制系统的稳定，易出现系统故障。为此本文利用模糊PID算法对双层振动筛自动筛分最优振幅进行控制。该方法具有结构简便、稳定性强等优势。但由于筛分系统具有非线性等特征，传统的PID 控制不能达到高精度要求。因此将其与模糊控制理论相结合，保留传统PID控制优势的同时增强其灵活性与适应性。利用本文设计的模糊PID控制器对于任意一种粒度的物料都有较高的筛分效率，且可以保持系统稳定，使筛分过程持续不间断进行。

2 筛分过程数学模型构建与物料运动规律分析

2.1 筛分动力学修正

自动振动筛为利用率最高的自动筛分设备，广泛使用在各大机械制造企业中，其种类繁多，功能也逐渐完善，但它们基本结构与工作原理相似。振动筛的结构主要包括激振器、箱体、弹簧、基座以及联轴器等零件。从进料端至出料端，此过程是全部机械结构合作完成，将电能转换为机械能达到振动目的。具体表现如下：在电机作用下，能量经过传递到达激振器，促使偏心装置旋转而形成激振力，并输出在箱体上，由于支撑弹簧的影响产生振动，以此开始工作。此外弹簧也有减震作用，可以减少达到基座的动力，与此同时阻尼装置还能保护弹簧不受损坏，延长设备使用寿命。

筛分过程的基本原理是物料的透筛概率论。为确定振幅对筛分过程的影响，达到最优控制目的，本文推导出一些筛分数学模型。

(1)概率学模型

此模型将单颗粒的透筛概率论当作基础，体现出颗粒和筛网发生碰撞后的透筛状况。结合颗粒与筛孔尺寸之间的关系，则单个颗粒垂直照射在水平筛面中的透射概率计算公式为：

公式中，a 表示筛孔大小，b为筛孔直径，d为颗粒粒度。则颗粒在筛面中经过第n次跳跃后仍不透筛的几率表示为：

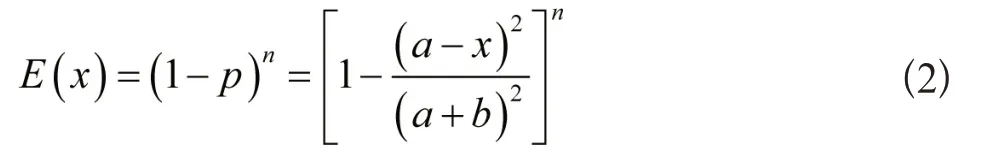
p表示相对颗粒垂直照射在水平晒面中的透射概率，x表示相对粒度。

(2)动力学模型

此模型将颗粒群当作分析目标，研究筛分效率与时间的关系，模型如下所示：

公式中，W0表示筛下物料质量，W表示筛上中包含筛下物料的瞬时质量，t为筛分所需时间，K属于比例系数，其大小与物料性质和筛面运动状态相关。

对公式(3)进行积分处理，能够获得筛分动力学方程：

公式中，J表示筛下物料在筛上物料中的分配率。

在实际过程中，公式(4)只适用于薄层筛分，无法在不同工况下使用，具有一定局限性。因此对其进行修正获得下式：

公式中，κ表示筛分设备的工作条件，若已知J在不同工况下与粒度之间的关系，则公式(5)就可以获得有效利用。

2.2 物料运动规律分析

物料在筛面上的三种状态分别为：相对静止、物料在筛面上滚动与跳动。但因为构成物料的颗粒大小不同，且没有规律地聚集在筛面上，如果此时筛面进行运动，则所有颗粒均会受到振动位移、速度等因素影响，且直接和筛面接触的是最下层物料，各颗粒之间又做独立运动，互相干扰，所以大颗粒跳跃后形成的间隙会由小颗粒进行填充。此外颗粒形状不统一，物料群体中还具有水分，因此物料运动规律十分复杂。

定常与混沌理论都能描述颗粒运动原理，它们都认为筛分机的抛射强度kv对颗粒运动状态产生一定影响。

其中定常理论在颗粒不出现滑动状况条件下，设定颗粒和振动筛面之间发生完全碰撞。如果kv＜1时，颗粒为滑动状态；如果kv=1，颗粒在滑动与跳跃的临界状态；如果kv＞1，则颗粒在筛面上进行跳动。

若0＜kv＜1时，颗粒会在筛面上与筛面一同运动，或与筛面进行相对滑动，且kv=1、kv=1．33 与kv=1．67 属于运动分叉点[5]。如果1＜kv＜1．67，颗粒运动可以利用稳定周期描述；如果kv＞1．67，经过两次分叉后出现混沌运动。

2.3 物料运动学参数确定

物料运动学参数表示了颗粒在筛面中的运动状态，筛分机处理性能取决于颗粒在筛面中的平均运动速度。本文在假设不发生滚动与滑动情况下，构建颗粒运动速度与筛分机运动学参数之间的关系函数，公式(6)与公式(7)分别表示颗粒分别在直线振动与圆振动筛面上平均运动速度表达式：

公式中，k0表示修正系数，α代表筛面倾斜角，β表示筛面上倾斜角，θ为跳跃角度，A是筛面振幅，n为跳跃次数。θ能够从颗粒跳跃初始角度φd的曲线中获得，而初始角φd与抛射强度之间存在如下关系：

通常条件下，直线振动筛与圆振动筛的k0取值分别为[0．6，0．8]和[0．13，0．15]。筛分过程的数学模型与物料运动的力学分析有助于探究振幅对筛分过程的影响，从而对振幅进行合理控制。

3 自动筛分最优振幅控制

3.1 振幅对自动筛分效率的影响

振幅属于自动筛分设备关键参数，振动幅值需要足够大，有助于减少堵塞现象[6]。但是幅值又不能过大，会限制频率，提升振动强度，从而降低设备使用寿命。振幅大小通常结合物料粒度尺寸来确定，针对较粗的筛可以利用大振幅，反之采取小振幅。为进一步分析振幅和筛分效果之间的关系。假设振动频率为f=15Hz、筛面倾斜角度与长度分别为α=20、L=700，振幅A分别为2．0mm、3．0mm、4．0mm与5．0mm。则不同振幅相对的颗粒运动速度情况如表1所示。

由表1能够得出，由于振幅的增加，筛分作业实现平稳状态所需时间逐渐缩短。这是因为在振幅较小时，筛面与颗粒之间作用较小，振幅增大，作用力变大，促使颗粒跳跃运动更加显著，因此很快达到稳定状态。此外，颗粒运动速度和振幅存在线性关系。

表1 振幅对应的颗粒运动速度表

通过拟合工具对振幅与颗粒运动速度做拟合处理，利用一次函数形式获取拟合结果。该结果表明振幅和颗粒运动速度具有一次方关系[7]。

分析表2可知，随振幅增加，筛分效率逐渐减小。整体表现为指数衰减态势。

表2 振幅与筛分效率关系表

因此，在实际筛分操作中，并不是振幅越小，筛分效率越高。振幅要根据颗粒大小进行适当调节，对其进行最优控制，减少物料堆积，才能提高筛分效率。

3.2 筛面上颗粒跳动目标函数

根据上述振幅对筛分效率的影响，确定目标函数。在振幅控制过程中，必须综合分析筛分设备处理性能与筛分效率两方面因素，在满足处理性能要求基础上，筛分效率越高。其数学模型表示为：

v表示颗粒运动速度，结合上述颗粒在筛面上经过n次跳跃后仍然不透筛的概率计算公式，获得筛分效率和不透筛之间的关系：

根据公式(9)分析得出：要想确保筛分效率最高，则不透筛概率J必须达到最小值，则优化后的目标函数为：

其中，k属于筛分常数，，x表示相对粒度。

颗粒在筛面中所有跳动次数计算公式为：

因此可以看出，影响n的变量包括f，α，A，L，在对振动筛进行设计时，将筛面长度看作是固定不变的，将其它参数作为变量，因此各变量之间关系为：

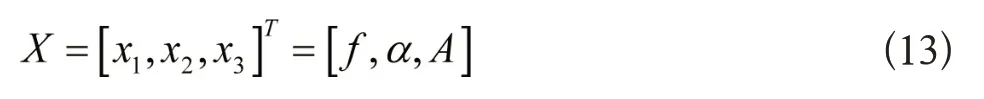
3.3 基于模糊PID控制器的最优振幅控制实现

确定筛面上颗粒跳动目标函数后，在传统PID控制器基础上，已知e表示初始振动筛的振动频率信号e，ec表示模糊控制后输出的振动筛振动频率信号，再结合模糊推理方式对PID的三个参数筛分时间Kp、筛分效率KI、颗粒大小KD做在线自动整定，来满足偏差与偏差变化率对控制器参数的要求，使被控目标具有一定的动静结合的能力。

筛分振幅控制PID参数的自动整合是挑选出其三个参数和e、ec之间的模糊关联，在工作状态下持续检测e、ec，结合模糊控制理论对三个参数做在线修订。分析三个参数在系统中起到的主要作用，在e、ec不同情况下，对PID控制器参数整合原则为：

(1)在筛分振幅控制输出响应初始状态在第一阶段时，|e|较大，为减少筛分振幅控制系统响应时间，避免由于开始时|e|快速变大，导致微分溢出，因此筛分时间Kp值应较大，颗粒大小KD值需较小。此外为抑制积分饱和[8]，防止系统响应产生超调，则要消除积分作用，令筛分效率KI值最大。

(2)在响应第二阶段，|e|取值为中等大小，为保证系统响应超调较小，筛分时间Kp取值需尽可能小。此种条件下，颗粒大小KD的取值会对系统产生较大影响，此外，筛分效率KI取值要尽量大。

(3)第三阶段中，|e|值较小，为提高系统稳定性，需同时增加筛分时间Kp与筛分效率KI的值，此外为抑制输出响应产生振荡，改善系统抗干扰性，颗粒大小KD值的确定原则是：当ec较低时，KD取值稍大；如果ec值较高，则KD取较小值。

在完成反模糊化处理后，根据不同控制参数的取值趋势，通过PID控制器实现对自动筛分振幅的最优控制。

4 仿真实验数据分析与研究

为证明本文控制方法性能，将煤当作筛分目标，利用的筛分设备材料为钢，煤和钢的物理参数信息如表3所示，其它参数如表4所示。

表3 煤和钢的物理参数表

表4 实验参数表

在本次筛分操作中，将筛分效率与系统输出波形作为评判指标，其中筛分效率表示物料质量占入料中低于筛孔大小的颗粒百分比，计算公式如下：

公式中，C表示筛下颗粒质量，Q是入料总量，a'表示入料低于筛孔尺寸的含量。

根据上述公式对球形颗粒与非球形颗粒使用不确定性高通量筛选系统的双子代数控制、双电动机驱动弛张筛及其伺服控制与本文方法的筛分效率进行计算，结果如表5所示。

表5 不同方法筛分效率对比表

由表5可知，当颗粒形状为球形时，三种方法都能保持较高筛分效率，但是当颗粒形状不规整时，不确定性高通量筛选系统的双子代数控制与双电动机驱动弛张筛及其伺服控制方法筛分效率降低。这是因为，模糊PID 控制方法可根据颗粒形状灵活调节控制参数，实现最优控制。此外图1是不同方法输出的控制波形示意图。

图1 不同方法控制波形示意图

从图1能够看出，本文方法输出的控制波形起伏平稳，表明筛分系统运行状况良好，而其它两种方法波形起伏较大，可能会出现故障。主要由于该方法在振幅控制前设定了准确的目标函数，合理抑制其它参数，避免系统超调，增强系统稳定性。

5 结束语

为提高不同种类物料的筛分效率，本文引入模糊PID控制法对双层振动筛自动筛分振幅进行最优控制。实验证明所提方法在提高筛分效率基础上还能改善系统稳定性，与其它方法相比控制性能优越。但是还需进一步研究更加精确的颗粒物之间碰撞检测算法，构建颗粒物之间力学接触模型，为振幅控制提供更多理论依据。此外，开发有限元软件接口，能够实时观察物料在筛面上的运动情况，掌握筛面应力应变。