二维随机跳频系统性能分析

宁晓燕， 梁洪广， 王震铎， 赵东旭

(哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001)

跳频技术具有抗干扰,抗截获等众多优点，在军用和民用领域中获得了广泛的研究和应用。针对跳频系统的干扰类型很多，窄带干扰是其中重要一种，而单音干扰是窄带干扰中非常常见的一种，对通信系统性能具有很强的影响。对于chirp基的分数域跳频来说，线性调频干扰是一种重要的相关干扰，研究其对跳频系统性能的影响是十分必要的。现有的针对跳频的抗干扰算法研究比较充分[1-7]，有一些学者也做出针对性的改进。文献[8]提出了一种基于伪随机线性调频的双序列跳频波形设计方法，该方法在复杂电磁环境下具有较好的抗干扰能力。文献[9]提出了一种基于跳频BOC的广义低歧义抗干扰扩频调制方法，该方法有效提高了全球导航卫星系统的抗干扰性能。文献[10-12]研究了FrFT类系统在变换域抗线性调频干扰及窄带干扰的性能，证明了合理的分数域传输能够一定程度上消除干扰的影响。

随着时代的发展，针对跳频信号的检测和截获技术也越来越成熟[13-19]，跳频信号在新技术下的抗截获能力随之降低。针对跳频信号抗截获能力降低的问题，文献[20]针对传统跳频需要预先共享信道密钥的问题提出了一种增加系统安全性的混沌跳频方法，可以在不使用预共享密钥的情况下提高信息传输速率并提高安全性。文献[21]通过子载波跳频的方法打乱传统WFRFT中离散傅里叶变换(DFT)矩阵列的顺序,从而使加权傅里叶变换矩阵的周期以及加权系数的周期在跳频序列的影响下呈现多样性,提高其抗截获的性能。文献[22]将FrFT与跳频系统相结合，选取固定变换阶次使系统在分数域进行跳频通信，有效提高了系统的频带利用率和抗截获性能，缺点是一旦非合作方获得固定阶次参数，则系统安全性仍然面临威胁。

本文为解决传统跳频参数变化单一，跳频信号易被截获的问题，提出一种基于分数阶傅里叶变换的二维跳频系统，利用跳频技术频率跳变对干扰的规避作用及合理的分数域传输对干扰的抑制作用提高系统抗干扰能力，利用分数域阶次的变换提高系统的抗截获能力。分析了系统在多径衰落信道下的性能、单音干扰和线性调频干扰下的抗干扰能力及时频分析手段下跳频周期和定时偏差2种参数的估计误差，为新的跳频体制设计提供参考。

1 二维随机跳频系统模型

基于分数阶傅里叶变换的二维随机跳频系统原理框图如图1所示。从图中可以看出，系统采用离散分数阶傅里叶变换的架构实现跳频信号的调制，其基信号为Chirp信号。采用2个不相关伪随机码分别控制载波频率的跳变及IDFRFT/DFRFT的变换阶次。

图1 系统原理Fig.1 System principle block diagram

离散时间信号的p阶分数阶傅里叶逆变换可以表示为：

(1)

基于FRFT的二维随机跳频过程可以看作对数据符号向量y=[y0y1…yN-1]T的编码及FrFT矩阵中变换阶次的随机选择：

Yp(k)=Dp(k)Cy

(2)

其中Yp(k)表示二维随机跳频信号向量，p(k)表示变换阶次的函数，Dp(k)表示变换阶次为p(k)(k=1,2,…)的IDFrFT变换矩阵，C为编码矩阵。基于FrFT的二维随机跳频信号可表示为：

(3)

其中α(k)=p(k)π/2。

从式(3)可以看出，使用DFRFT调制生成的子 载波是一系列调频率为0.5cot(α(k))的线性调频信号，频率随时间线性变化，第n个子载波函数的频率为：

(4)

当输入信号码元时间宽度保持不变时，即t保持不变时，ωn随着变换阶次的变化而变化，线性调频信号扫过的带宽也不断变化,信号每一跳都有不同的中心频点和子载波带宽。系统子载波的交叠程度较高，跳频图案如图2所示，某一阶次下某一跳信号子载波的选取如图3所示。

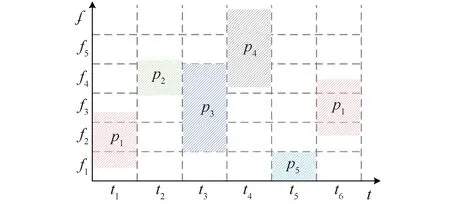
图2 二维随机跳频图案Fig.2 Two-dimensional random frequency hopping pattern

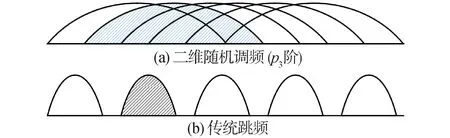
图3 某一阶次下某一跳信号子载波选取与传统跳频对比Fig.3 Comparison of subcarrier selection of a certain hop signal and a certain order with traditional frequency hopping

2 系统性能分析

2.1 误码率性能分析

2.1.1 高斯白噪声下

假设跳频子载波总数为N，某时刻信号在第n个子载波上传输，此时发射信号可表示为：

(5)

为方便分析，系统框图中给出的调制方式为QPSK调制，实际亦可采用其他调制方式，因此a为QPSK调制数据符号。

假定系统收发双方处于理想同步状态下(仿真过程亦为理想同步)，接收端接收信号为有用信号s(t)和高斯白噪声信号n(t)的加和。假设信道中的高斯白噪声信号n(t)服从均值为0，方差为σ2的高斯分布，即n(t)～N(0,σ2)。分数阶傅里叶变换为线性变换，噪声在接收端经分数阶傅里叶变换后仍服从高斯分布，即N(t)～N(0,σ2)。

接收端接收信号经分数阶傅里叶变换后变为调制映射符号数据与高斯白噪声的叠加，因此本系统的误码率理论上与所用调制方式的相干接收误码率一致。信号通过接收机后判决量u(t)可表示为：

(6)

式中F(·)表示对信号进行分数阶傅里叶变换。

系统在高斯白噪声信道下的误码率为：

(7)

其中r=a/2σ2。

从式(7)可以看出，系统在高斯白噪声信道下误码率与所用QPSK调制的理论误码率一致，分数阶傅里叶变换并未提升系统在高斯白噪声信道下的性能。但由于分数阶傅里叶变换的基信号是chirp信号，具有一定的抗多普勒频移的能力，在时频双选衰落信道下具有更好的表现。

2.1.2 单音干扰下

单音干扰为：

J(t)=Aexp(j2πft+jθ)

(8)

系统受音频干扰影响示意图如图4所示。当信道中存在单音干扰时，传统跳频有较少频点受干扰的影响，二维随机跳频系统由于子带交叠程度高，与之相邻的多个子带都会收到一定的影响。

图4 单音干扰影响示意Fig.4 Schematic diagram of single-tone interference

通过数学推导分析单音干扰对系统性能影响。为方便观察系统性能，分析在固定功率单音干扰下，系统误码率随信噪比的变化情况。

接受端接收信号可表示为有用信号、单音干扰及高斯白噪声的叠加，经分数阶傅里叶变换后的信号可表示为：

(9)

不失一般性，假设选择N个子载波中的第n个子载波进行信号传输，则判决变量为：

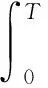
πfsec(α(k))T2)

(10)

被干扰子载波上传输信息的误码率为：

(11)

其中：

(12)

由式(11)可得，被干扰子载波上传输信息的误码率与信号功率、干扰功率、背景噪声功率及所用分数阶傅里叶变换的变换阶次有关。

假设L跳信号中有l跳被干扰，则系统总误码率：

(13)

从式(13)可以看出系统总误码率由2部分组成，一部分是被干扰子载波上传输信息的误码率，另一部分是背景噪声下子载波上传输信息的误码率。当系统信噪比逐渐增大，背景噪声对系统的影响逐渐减小，系统误码率的大小主要受干扰的影响。

2.1.3 线性调频干扰下

线性调频干扰信号可以表示为：

J(t)=Aexp(jμt2)

(14)

线性调频信号可看作宽带噪声干扰，其总功率在子载波带宽的一部分ρ,0<ρ<1上分布，ρ表示子带所受干扰比例。

通过数学建模分析线性调频干扰对系统性能影响。为方便观察系统性能，分析干扰在固定功率情况下，对系统误码率的影响。

线性调频干扰在接收端经分数阶傅里叶变换后变为：

(15)

此时判决变量u(t)为：

(16)

被干扰子载波上传输信息的误码率为：

(17)

其中：

(18)

假设H跳信号中有h跳被干扰，则系统总误码率：

(19)

由式(19)可得，系统的总误码率受干扰及背景噪声的双重影响。根据式(18)可以看出当线性调频干扰信号的调频率μ与分数阶傅里叶变换的变换阶次p(k)满足：

(20)

可以最大程度降低线性调频干扰对系统的影响。

2.2 抗截获性能分析

2.2.1 功率谱

首先对发射信号s(t)进行傅里叶变换得：

(21)

引入菲涅尔积分公式，对式(21)化简得：

(22)

其中：

(23)

(24)

式中CF(x)和SF(x)为菲涅尔积分公式。

根据Parseval定理，信号的功率谱密度为:

(CF(x(f))+jSF(x(f)))2

(25)

从式(25)可以看出，信号的功率谱密度会随着变换阶次的变化而发生变化。由FRFT的周期性知，变换结果是变换阶次p的周期函数，因此上述信号的功率谱密度同样随着变换阶次的变换存在着周期性的变化。

2.2.2 跳频周期估计方法

为验证二维随机跳频信号具有较好的隐蔽性，选择常用的信号参数估计手段对信号进行分析，这里采用的时频变换方法是短时傅里叶变换，选择的待估计参数为跳频周期和定时偏差。

假设窗函数宽度为N，对信号进行短时傅里叶变换，随着窗函数向该频点信号中间时刻滑动，信号谱线强度先增大后减小。所得时频分析矩阵中每个时刻所对应的最大值y(n)及最大值对应的位置p(m),m=1,2,…，M。p(m)即为待估计信号各个跳点的中间时刻。

y(n)=max{TFD(m,n)},n=1,2,…，N

(26)

式中TFD(m,n)为信号时频分布矩阵。

己知任意2个峰值之差应为周期点数Nh，利用最后一个峰值p(M)与第1个峰值p(1)之差，后除以M-1即可得到估计值Nh：

(27)

得到周期点数估计值Nh后，利用公式Th=Nh/fs便可得到跳频周期的估计值。

在后续仿真时，为定量描述该方法对信号参数估计的能力，定义跳频周期估计误差占跳频周期百分比α：

(28)

式中TH为实际跳频周期。

2.2.3 定时偏差估计方法

为保证接收端接收信号的起始点为跳频信号某一跳的起始位置，必须首先确定接收信号起点与下一个频率跳变时刻之间的时间差，即定时偏差。

已知p(m)为各跳中间时刻，在理想状态下，p(m)是一个以NH为公差的等差数列，数列点数为M。则该数列的求和公式为：

(29)

式中p1为该等差数列的首项。

利用跳周期点数估计值NH，可以估计出p1的值，该值即为第1个峰值出现的位置：

(30)

利用公式Td=Nd/fs，便可以实现定时偏差的估计。

在后续仿真时，为定量描述该方法对信号参数估计的能力，定义定时偏差估计误差占实际定时偏差百分比：

(31)

式中TD为实际定时偏差。

3 仿真结果

3.1 误码率性能仿真分析

3.1.1 高斯白噪声信道及衰落信道下

二维随机跳频系统在高斯白噪声信道下性能仿真如图5所示。子带总数为64，变换阶次的变化范围为0.4～1.6。从图中可以看出，仿真结果与理论结果一致，即为QPSK调制的理论误码率，验证了理论推导的正确性。

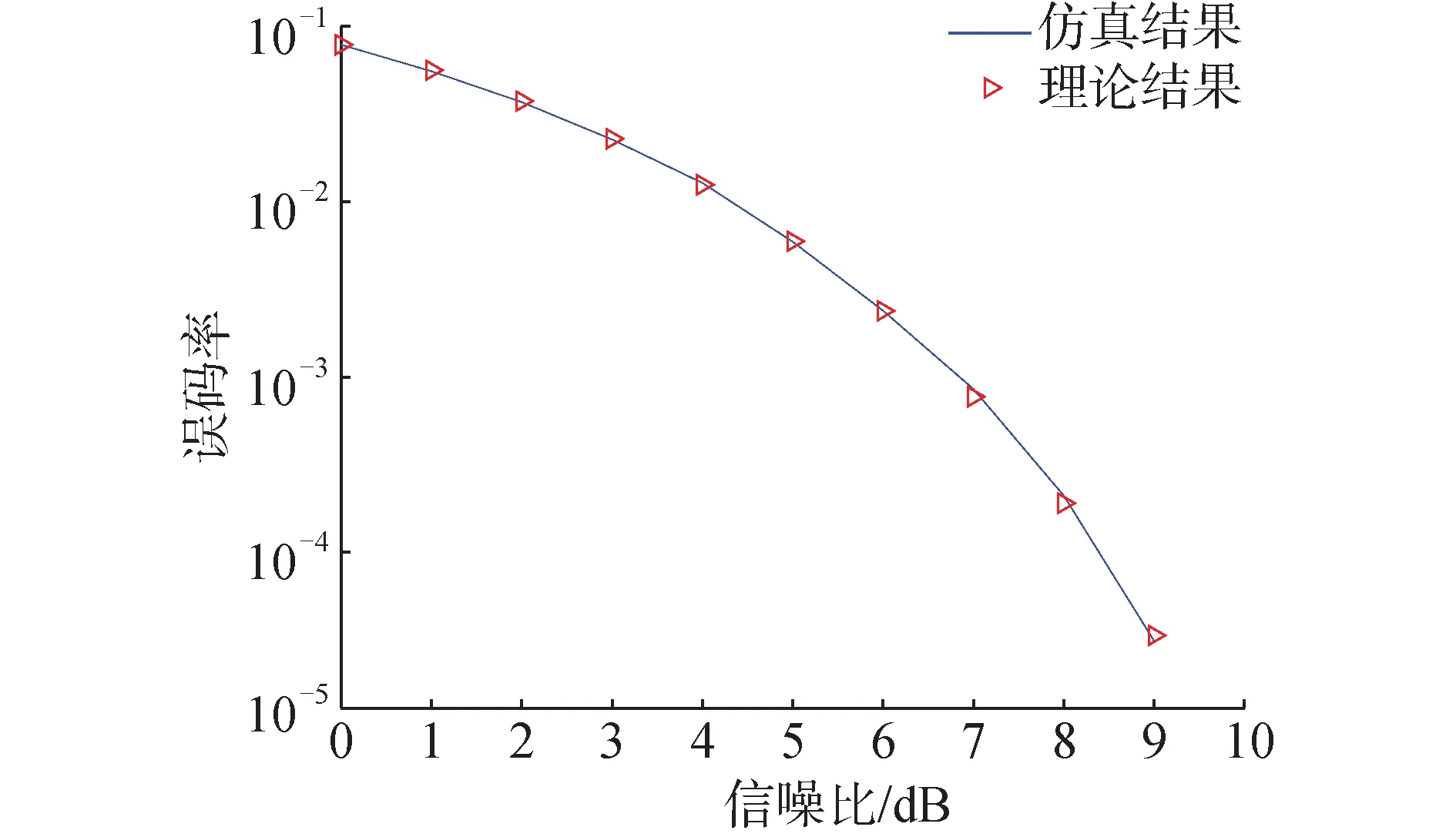
图5 高斯白噪声下二维随机跳频系统性能Fig.5 Performance of two-dimensional random frequency hopping system under Gaussian white noise

对衰落信道下多径和多普勒频移对系统性能影响进行仿真分析。设置信道中多径数量为4，每径的时延分别为0、1、2.5、3 ms，每径的衰减分别为0、2、3、5 dB，归一化多普勒频移fd为3×10-6。在接收端，接收机只选择能量最大的主径进行接收。并与传统跳频系统进行对比，仿真结果如图6所示。

图6 衰落信道对二维随机跳频系统影响Fig.6 The influence of fading channel on two-dimensional random frequency hopping system

图6中FRFT-FH表示基于分数阶傅里叶变换的二维随机跳频系统，Trad-FH表示传统跳频系统。从图中可以看出，多径和多普勒的存在会增大系统正常通信所需信噪比。在fd为3×10-6时，正常通信所需信噪比约增大4 dB。而且在相同条件下，FRFT-FH系统抗多普勒频移的性能要优于传统跳频。

3.1.2 单音干扰下

对高斯白噪声背景下，固定功率单音干扰对系统影响进行仿真，仿真结果如图7所示。为方便观察，选择传统跳频进行对比，设置64个子带，调制方式为QPSK，信干比固定为5 dB，分数阶傅里叶变换的阶次变化范围为0.3～0.8。

图7 单音干扰下系统误码率曲线Fig.7 System bit error rate curve under single tone interference

从图中可以看出，当存在有单音干扰时，仿真结果都与理论结果相符，验证了理论推导的正确性。虽然二维随机跳频系统的子带重叠率高，受单音干扰影响的子带数量多，低信噪比时2个系统的性能大致相同，但在高信噪比下，二维随机跳频系统抗单音干扰的能力要优于传统跳频系统。原因是单音干扰经分数阶傅里叶变换后变得平坦，虽然影响的子带数较多，但对于每个子带的影响很小，相当于多个子带共同承受单音干扰的影响。

在较高信噪比时，系统的误码趋于平缓的原因是分数阶傅里叶变换只能减弱单音干扰带来的影响，不能完全消除。二维随机跳频系统带来的这种效果更容易与纠检错编码配合，降低通信所需的信噪比下限。

3.1.3 线性调频干扰下

当信道中既存在高斯白噪声，又存在固定功率的线性调频干扰时，二维随机跳频系统误码率性能如图8所示。选择传统跳频系统进行对比，子载波数量为64，调制方式选择QPSK，信干比固定为5 dB，分数阶傅里叶变换的阶次变化范围是0.3～0.8。线性调频干扰信号的调频率为0.72，对应分数阶傅里叶变换的变换阶次为-0.6阶。

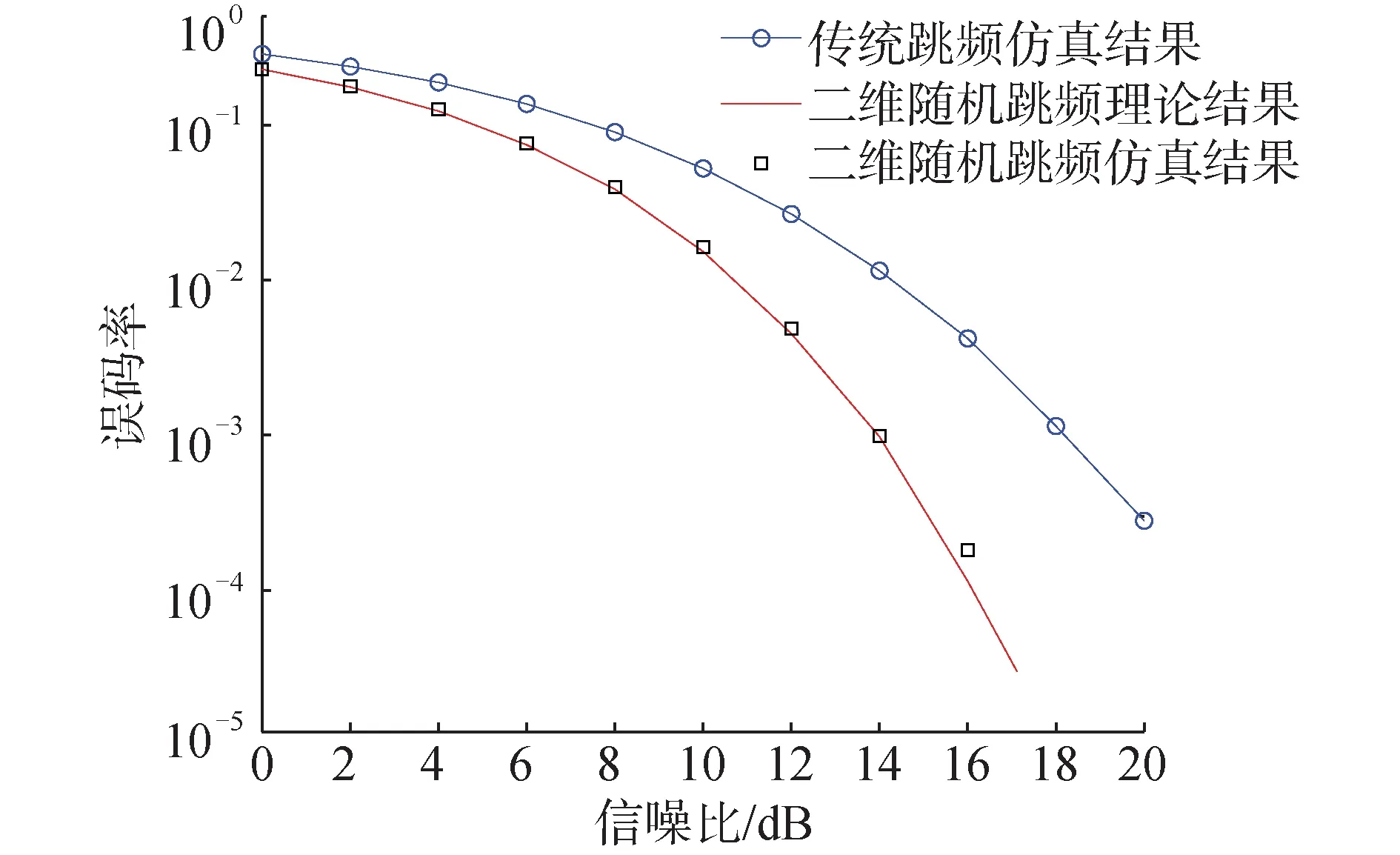
图8 线性调频干扰下系统误码率曲线Fig.8 System bit error rate curve under chirp interference

从图8中可以看出，二维随机跳频系统在线性调频干扰下的理论误码率与实际仿真误码率一致，验证了理论推导的正确性。对比图中FRFT-FH仿真曲线和Trad-FH仿真曲线可以发现，二维随机跳频系统具有更强的抗线性调频干扰能力。

不难发现，线性调频干扰的存在会提高系统正常通信所需信噪比，而且二维随机跳频系统的基信号是Chirp信号，如果选择与线性调频干扰信号调频率相对应的变换阶次进行通信，能够有效减弱线性调频干扰带来的影响。

3.2 抗截获性能仿真分析

3.2.1 功率谱

二维随机跳频系统以Chirp信号为基信号，其功率谱呈平坦状。选取第5、16、31、50个子带信号进行功率谱分析得到的子带信号功率谱如图9所示。

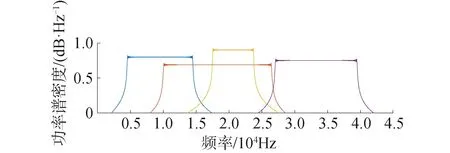
图9 二维随机跳频系统多个子带信号功率谱Fig.9 Power spectrum of multiple subband signals in two-dimensional random frequency hopping system

从图9中可以看出，FRFT-FH系统的谱交叠程度非常大，频谱利用率高。每跳信号的变换阶次不同，信号带宽也不同，有效地减弱了信号周期性。

3.2.2 跳周期估计误差

为方便观察，依然选择与传统跳频系统对比。跳频周期均设置为6.4 ms。为避免偶然性，随机截取时间长度为6.4 s的信号进行多次跳频周期估计后取平均值。其估计误差平均值占跳周期的百分比随信噪比变化如图10所示。

图10 跳频周期估计误差占跳频周期百分比Fig.10 Frequency hopping period estimated error as a percentage of frequency hopping period

从图10中可以看出，相同跳频周期相同估计算法下，FRFT-FH信号的估计误差要远大于传统跳频。其原因是时频估计算法非常依赖时频窗的选择，而在FRFT-FH系统中，随着变换阶次的不断变化，信号的带宽也在不断变化，若固定时频窗函数的长度，则很难对信号参数进行有效估计，误差必然很大。

3.2.3 定时偏差估计误差

定时偏差设置为4 ms，为避免偶然性，对1 000段定时偏差相同的信号进行分别估计，取估计结果的平均值。其估计误差平均值占总定时偏差的百分比随信噪比变化如图11所示。

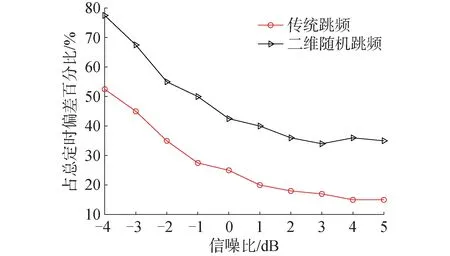
图11 定时偏差估计误差占定时偏差百分比Fig.11 Timing deviation estimation error as a percentage of timing deviation

从图11中可以看出，FRFT-FH信号的定时偏差估计性能更差。首要原因是时频变换非常依赖窗函数的选择，变换阶次的变化会改变信号带宽，降低了时频分析手段的精度。其次，定时偏差估计结果需基于跳频周期估计结果，存在误差的累积。

4 结论

1)本文提出一种基于FRFT的二维随机跳频系统，通过改变FRFT的变换阶次改变每个码元信号的带宽，进而改变信号的周期特性，增加信号的随机性，配合跳频改变信号中心频率，形成二维随机跳频系统。

2)该系统在高斯白噪声下性能与所用调制方式理论误码率一致，在衰落信道下通信所需信噪比约提高4 dB，且相同条件下优于传统跳频

3)二维随机跳频系统能够一定程度上抑制单音干扰的影响，并不能完全消除，且抑制单音干扰的能力强于传统跳频；当信道中存在线性调频干扰时，二维随机跳频系统能够极大程度上抑制线性调频干扰的影响，其性能也优于传统跳频。

4)在隐蔽性能方面：变化的变换阶次及中心频率造就了信号的非平稳特性，由于信号带宽的不断变化，使得在使用时频分析手段对二维随机跳频信号的跳频周期及定时偏差进行估计时，估计误差要大于传统的一维跳频，即二维随机跳频信号具有更好的抗截获性能。