宽厚比为5的超高层建筑风荷载特性研究

2022-03-11韩振李波甄伟杨庆山田玉基

哈尔滨工程大学学报 2022年2期

韩振，李波,2，甄伟，杨庆山，田玉基,2

(1.北京交通大学土木建筑工程学院，北京 100044；2.结构风工程与城市风环境北京市重点试验室，北京 100044；3.北京市建筑设计研究院有限公司，北京 100045；4.重庆大学土木工程学院，重庆 400044)

超高层建筑是现代城市的重要组成部分，具有阻尼小，频率低的特点，是典型风敏感结构。随着人们对采光、通风等宜居性需求的增强，大宽厚比超高层建筑越来越多，例如：迪拜海湾沙滩大厦，杭州高德置地广场等，宽厚比均超过了3。宽厚比是影响钝体来流绕流特征及表面风压分布的主要因素，早期研究者以二维矩形钝体为对象，对宽厚比的影响展开了研究。Okajima[1]通过风洞试验对宽厚比为1～4的二维矩形钝体进行了研究，给出了不同宽厚比矩形钝体Strouhal数随Re数的变化。Norberg[2]通过风洞试验，得到了不同宽厚比二维矩形钝体的气动力系数随风向角的变化。Yu等[3-5]则重点分析了不同宽厚比二维矩形钝体的来流绕流特征和风压分布规律。郑云飞[6]在不同宽厚比二维矩形截面两端设置端板，研究了端板尺寸对各模型气动特性的影响。王新荣等[7]还研究了均匀湍流场条件下，不同宽厚比二维矩形钝体的风压特征及其雷诺数效应。通过系列研究，已经掌握二维矩形钝体的绕流及其风压分布特征。但是，超高层建筑是三维钝体[8]，并且还需要考虑大气边界层的影响。Lin[9]通过测压风洞试验研究了宽厚比为0.34～2.98的超高层建筑风荷载特性，对比了不同宽厚比超高层建筑层风力系数及基底力矩系数等，为结构抗风设计提供了参考。李永贵[10]以宽厚比为自变量，给出了矩形截面高层建筑根方差扭矩系数和基底扭矩功率谱的计算公式。Tamura[11]、顾明[12-13]在其不同形体超高层建筑风荷载特性系列研究中，包括了宽厚比为1和2的矩形超高层建筑。可以看出，具有较大宽厚比的超高层建筑与方形截面超高层建筑相比，侧风面可能发生分离流再附，绕流机制将发生改变，风荷载特性将可能不同。但受以往工程实践的限制，并未展开深入研究。

本文以一栋宽厚比D/B=5的工程实例为背景，通过测压风洞试验得到了大宽厚比超高层建筑风荷载，并将结果与东京工艺大学完成的宽厚比D/B=1的超高层建筑风洞试验数据对比，说明了大宽厚比超高层建筑侧风面再附现象，给出了风荷载特征，旨在为类似工程提供参考。

1 风洞试验

1.1 试验模型及风场

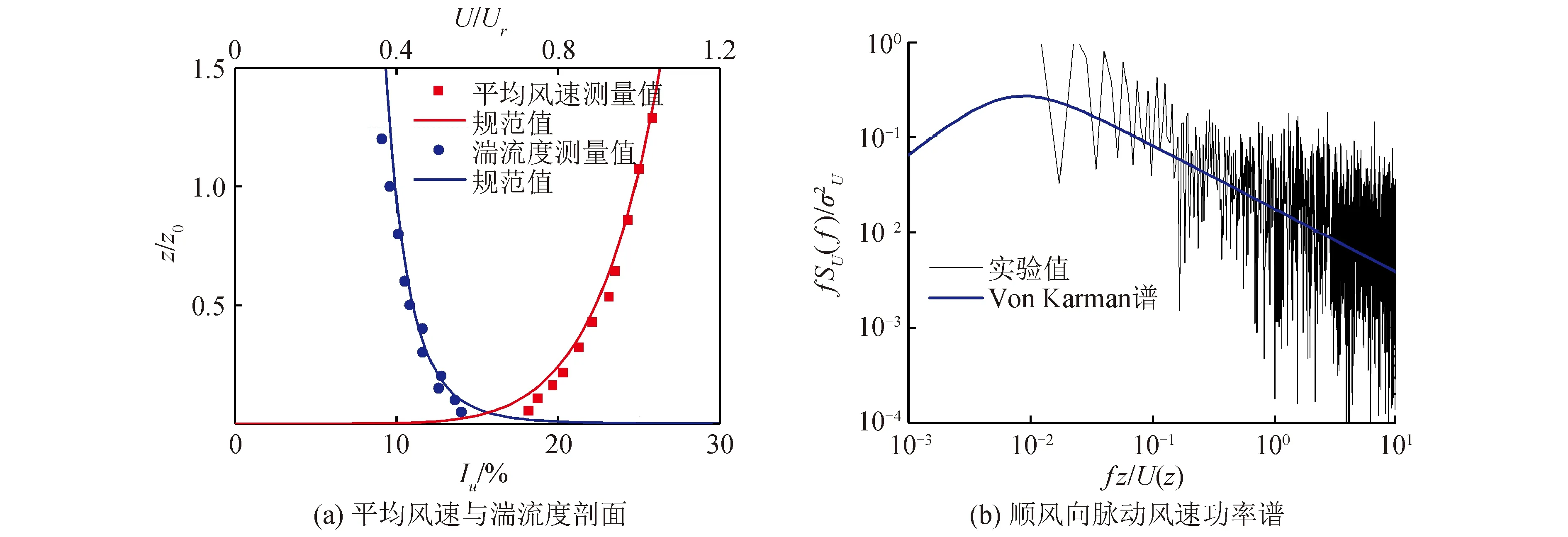
图1 试验风场Fig.1 Testing wind flow

风洞试验模型如图2所示，采用ABS材料制作，宽厚比D/B=5，几何缩尺比为1∶200。建筑外立面布置了10层测点，每层35个，共计350个测点，建筑x向(沿建筑长边方向)和y向(沿建筑短边方向)对应的风向角分别为0°和270°，T为绕体轴的扭转。风洞试验中，通过电子压力扫描阀测量模型表面风压，采样频率为312.5 Hz，每个测点连续采集20 000个样本。

图2 试验模型及测点布置Fig.2 Testing model and taps distribution

选取东京工艺大学空气动力学数据库中宽厚比D/B=1的超高层建筑风洞试验结果用于对比分析，该试验与本次试验风场均为郊区地貌类别，风剖面幂指数α=1/6。

1.2 数据分析方法

在分析建筑表面风压时，通常采用无量纲压力系数Cpn表示[14]：

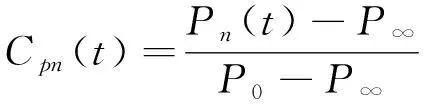
(1)

式中：Cpn(t)为测点n处t时刻的压力系数，Pn(t)为扫描阀在测点n处t时刻测量的压力值，P0和P∞分别是参考高度处的总压和静压。

将模型某一测点层内所有测点表面的风压系数按测点代表面积分别向垂直于建筑短边x和长边y两个方向合成，可得到该测点层高度范围内总的x向、y向及扭转向风荷载，即层三分力，根据各层层三分力可求得基底力矩，然后再进行无量纲化处理即可得到层三分力系数和基底力矩系数：

(2)

(3)

(4)

2 试验结果

2.1 风压系数

图3给出了宽厚比D/B=1，5的超高层建筑在0°风向角时，2/3高度处平均风压系数分布图。

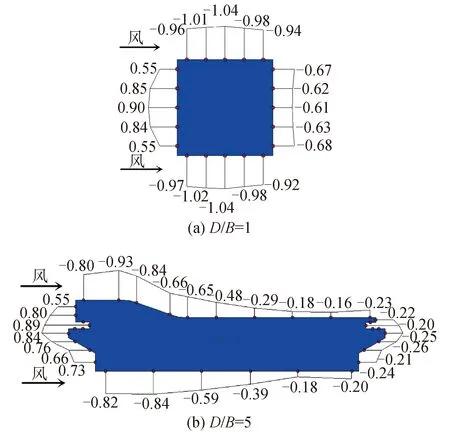
图3 建筑物2/3高度处平均风压系数分布Fig.3 Distribution of mean wind pressure coefficient at 2/3 height of buildings

可以看出，2种宽厚比建筑，迎风面平均风压均为正值，其分布规律、大小相似；侧风面受流动分离的影响，风压均为负值，但大小受宽厚比的影响较大。D/B=1时，平均风压沿侧风面变化梯度很小，呈先增大后减小的趋势，而D/B=5时，平压风压变化梯度增大，在侧风面4/5处达到最小值后，又小幅上升；背风面受尾流的影响，风压均为负值，且大小同样受宽厚比影响较大，D/B=5时的背风面风压仅为D/B=1时的1/3。结合二维矩形钝体分析结果[5]，由以上现象可以推得，D/B=1时，侧风面整体处于分离剪切层形成的分离泡中，且尾流较宽，侧风面、背风面均产生较大的负压。D/B=5时，分离流在侧风面发生了再附，且在下游角点发生二次分离，使得侧风面风压梯度变化明显，再附同时使尾流变窄，导致背风面风压减小。

图4给出了宽厚比D/B=1，5的超高层建筑在0°风向角时，2/3高度处脉动风压系数分布图。

图4 建筑物2/3高度处脉动风压系数分布Fig.4 Distribution of fluctuating wind pressure coefficient at 2/3 height of buildings

可以看出，对于脉动风压，当建筑宽厚比增大后，无论是迎风面，侧风面还是背风面，风压值均有所减小。值得注意的是D/B=1时，脉动风压沿侧风面逐渐增大，在尾部达到最大值；而D/B=5时，脉动风压在侧风面的分布总体呈先增大后减小的趋势，变化较为复杂。文献[15-17]认为侧风面脉动风压极值点的位置为再附点，用无量纲参数L/D表示侧风面的相对位置，其中L为侧风面某位置到迎风面前缘的距离。由图4(b)可以看出，侧风面Ⅰ (上)再附点出现在L/D=0.46处，侧风面Ⅱ (下)出现在L/D=0.57处。需要说明的是，侧风面Ⅰ (上)虽然在L/D=0.16处出现了脉动风压最大值，但该处主要是受不规则形体的影响，并不是气流再附点位置。

表1给出了宽厚比D/B=5的超高层建筑，不同高度处侧风面再附点的位置。

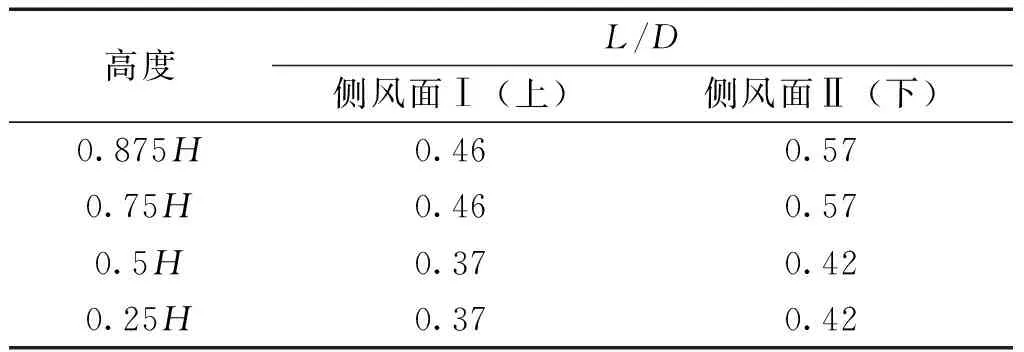
表1 侧风面再附点位置(D/B=5)

可以看出，建筑不同高度处再附点的位置有所不同，建筑物上部侧风面再附点的位置相比于中、下部位置靠后。该现象表明再附点位置与湍流度有关，建筑上部相比于中下部湍流度较小，分离流较强，因此再附点向后移动，与文献[16-17]结论相吻合。

图5给出了2种宽厚比建筑2/3高度处，侧风面不同位置的测点与前缘测点的风压相关系数。

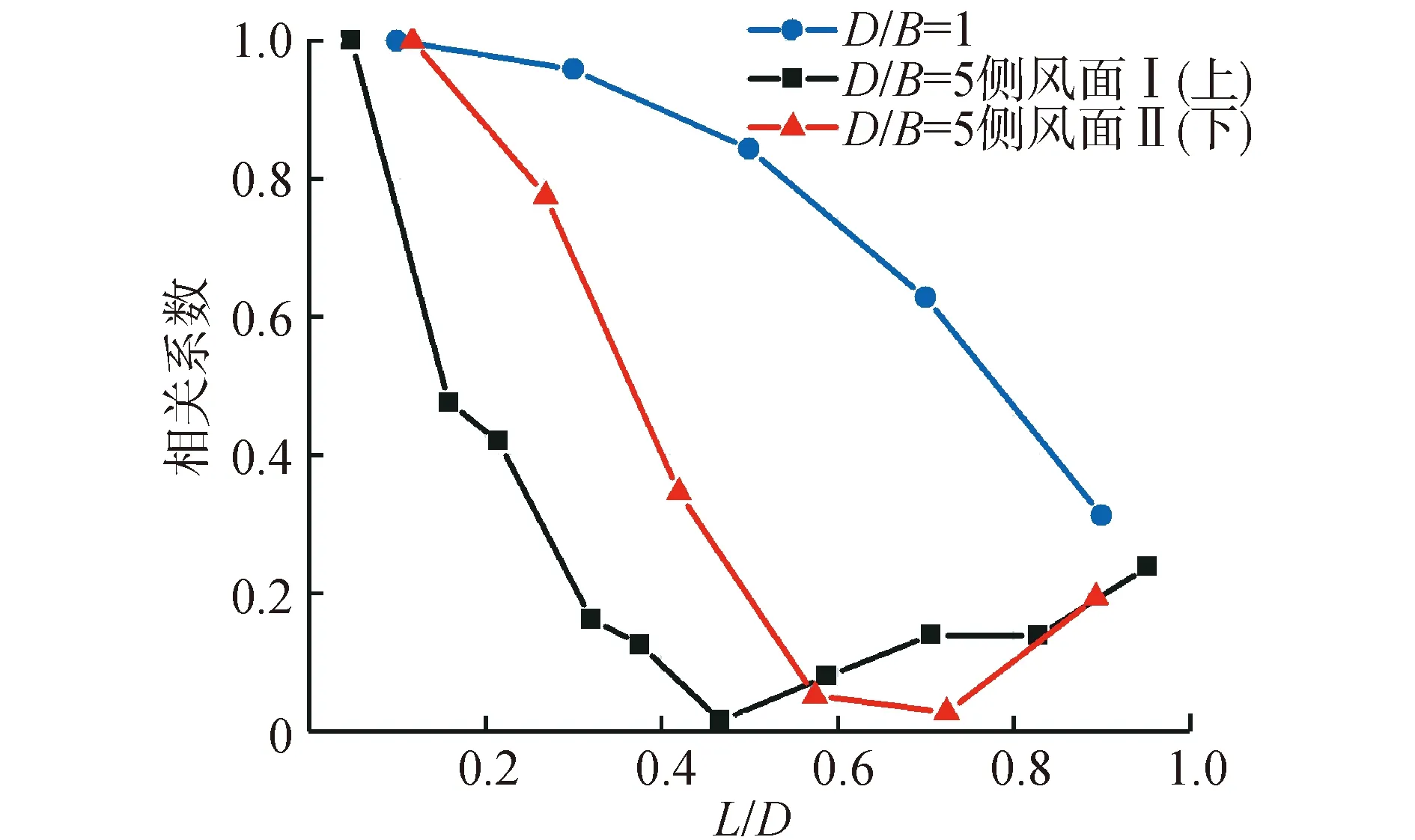
图5 建筑2/3高度处侧风面脉动风压相关性Fig.5 Correlation of fluctuating wind pressure on the sideward surfaces at 2/3 height of buildings

可以看出，宽厚比D/B=1时，侧风面风压相关系数衰减速度较慢，各测点的相关程度较高。D/B=5时，侧风面风压相关系数衰减速度大幅加快，再附点附近相关系数接近于0，而后有小幅增大的趋势。这也说明了D/B=1时，侧风面整体处于分离剪切层形成的分离泡中，风压作用机制相同，相关性强；D/B=5时，侧风面发生了分离流再附，而后又在下游角点处发生二次分离，再附点附近风压作用机制发生改变，导致侧风面风压相关性降低。

2.2 层风力系数

图6给出了2种超高层建筑在0°风向角时，x向(Cx)、y向(Cy)和扭转向(CT)层风力系数沿建筑高度的分布。

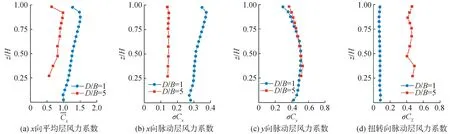
图6 层风力系数沿建筑高度变化Fig.6 Variation of local wind force coefficients along the height of buildings

可以看出，2种宽厚比超高层建筑x向平均层风力系数随建筑高度的增加总体上呈增大趋势，最大值出现在高度0.9H左右，D/B=1、5对应的最大值分别为1.51和0.99，顶部由于受到三维绕流效应的影响，平均层风力系数减小。受分离流再附影响，D/B=5时尾流变窄，背风面平均风压减小，导致x向平均层风力系数整体小于D/B=1；对于x向脉动层风力系数，其变化规律与平均层风力系数较为相似，D/B=5时x向脉动层风力系数同样小于D/B=1；宽厚比对y向脉动层风力系数影响很小，均沿建筑高度的增加先增大后减小，且数值大小相近；扭转向脉动层风力系数在D/B=1时较小，不同高度处基本保持在0.08左右，而D/B=5时，扭转向层脉动风力系数整体较大，在建筑0.37H高度处出现最大值0.49。

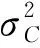
图7 层风力系数功率谱Fig.7 Power spectrum of local wind force coefficients

可以看出，2种宽厚比超高层建筑，x向脉动层风力系数功率谱较为相似，总体呈宽带过程，且不同层之间功率谱曲线变化基本一致；对于y向，D/B=1时，功率谱呈窄带过程，在折减频率0.09处出现一个与漩涡脱落有关的尖峰，能量较为集中。而D/B=5时，功率谱频带变宽，出现2个能量相当的谱峰，低频谱峰对应的折减频率范围为0.04～0.08，高频处的谱峰仅在建筑中上部出现对应折减频率为0.15；对于扭转向，D/B=1时，在折减频率0.06～0.09及0.2～0.3处出现2个谱峰，而D/B=5时，仅在折算频率0.13附近出现一个谱峰。

2.3 基底力矩系数

图8给出了0°风向角时，2种宽厚比超高层建筑基底x向(CMx)、y向(CMy)及扭转向(CMT)力矩系数间的相位轨迹图，其中ρ为相关系数。

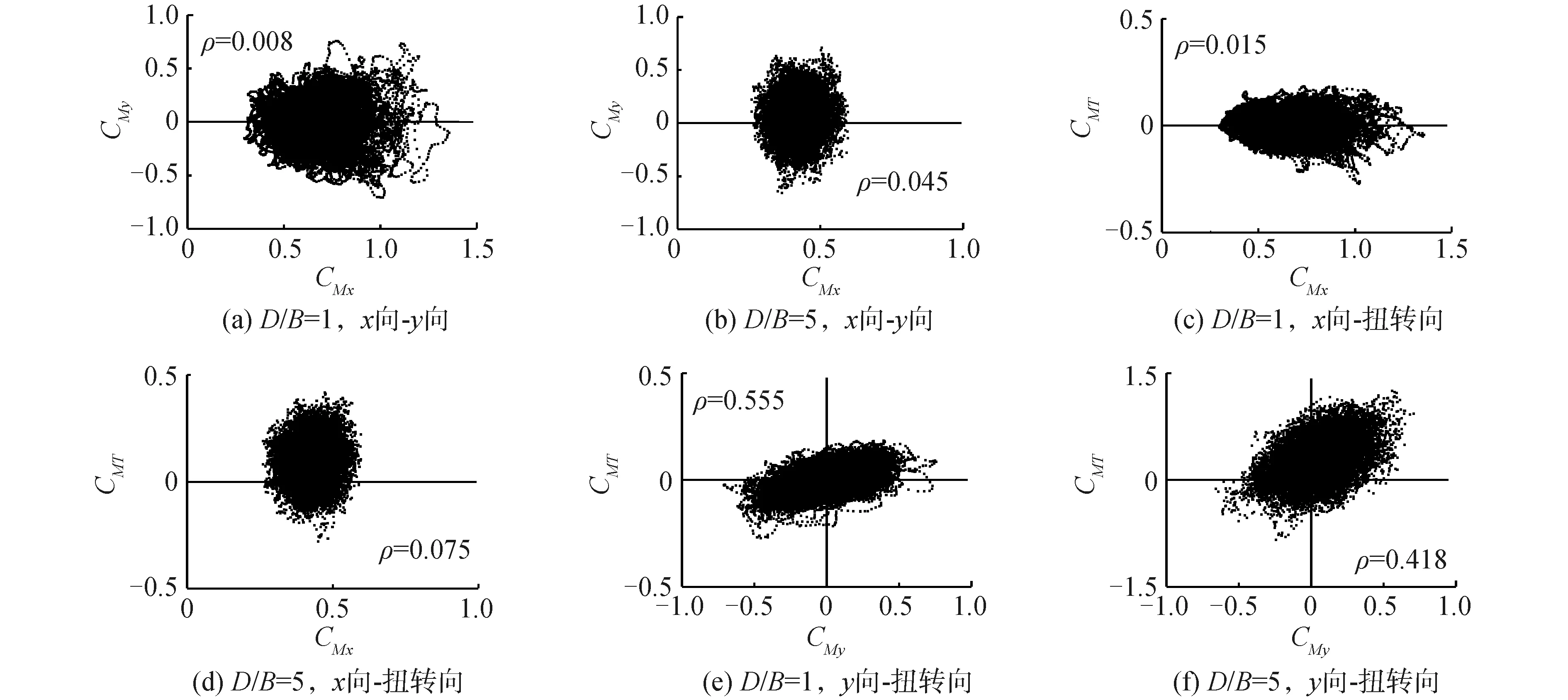
图8 基底力矩系数间相位轨迹图Fig.8 Phase-plane trace of base moment coefficients

可以看出，建筑基底x向-y向、x向-扭转向力矩系数间相位轨迹呈椭圆形，且椭圆形长轴和短轴几乎与坐标轴平行，D/B=1，5时的相关系数分别为0.008、0.015和0.045、0.075，相关性均较差；而y向-扭转向间椭圆轨迹具有一定的斜率，D/B=1，5时的相关系数分别为0.555和0.418，相关性较强，但随宽厚比的增大相关性减弱。

根据建筑基底力矩系数在0°风向角时的时程，表2给出了建筑基底某一主方向力矩系数达到极值时，从方向力矩系数的同步值。可以看出，尽管两种超高层建筑基底x向-y向、x向-扭转向间的相关系数很小，但当基底y向和扭转向力矩系数分别取得极值时，x向同样会取得较大值，具有极值相关性；同理基底y向和扭转向间也存在较强的极值相关性，且随宽厚比增大极值相关性增强。

表2 基底力矩系数极值与同步值Table 2 Maximum and synchronous value of base moment coefficients

图9给出了0°风向角时，两种宽厚比超高层建筑基底力矩系数间的相干函数曲线。

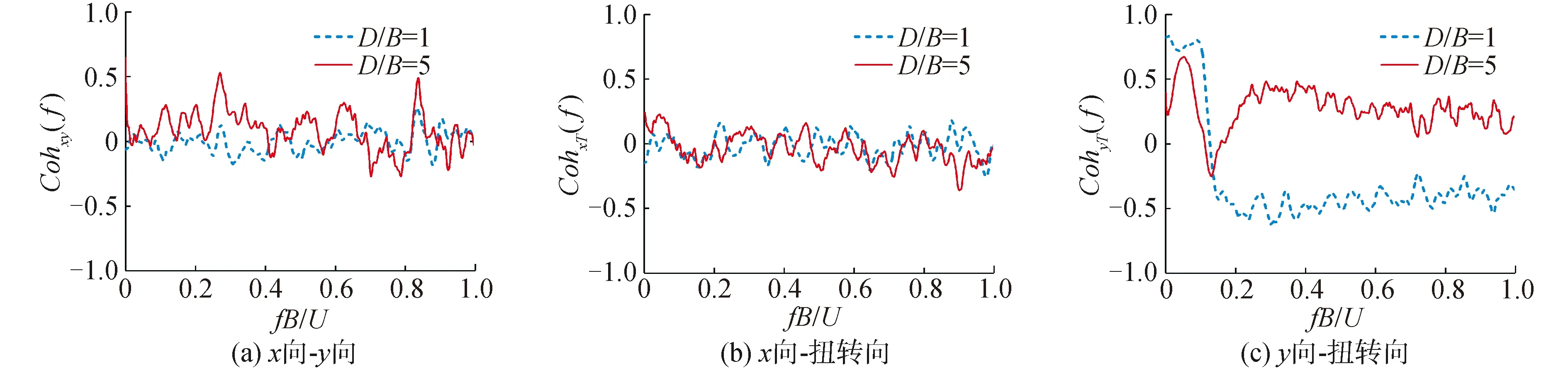
图9 基底力矩系数相干性Fig.9 Coherence of base moment coefficients

可以看出，2种宽厚比超高层建筑基底x向-y向、x向-扭转向力矩系数间的相干函数无明显规律性，在0左右上下波动，相干性均较差；y向-扭转向在0≤fB/U≤0.2范围出现明显峰值，D/B=1，5时对应的峰值大小分别为0.81和0.67、-0.25，相干性均较强，且峰值位置对应的折减频率与y向脉动层风力系数功率谱峰值位置的折减频率相近。当fB/U>0.2时，相干函数曲线逐渐稳定在某一值范围内，其中D/B=1，5对应的稳定值分别约为-0.38和0.20。