基于Shell-Solid单元混合建模技术的焊接数值模拟方法
2022-03-11李陈峰王庭策刘葳蔡庆港董森周学谦
李陈峰, 王庭策, 刘葳, 蔡庆港, 董森, 周学谦
(1.哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨 150001;2.船舶与海洋工程技术教育部国际合作联合实验室,黑龙江 哈尔滨 150001)
焊接贯穿船舶与海洋平台整个建造过程,焊接工艺的好坏直接影响其建造精度与质量。随着计算机技术的发展,焊接数值模拟作为焊接试验的重要补充,日益成为焊接性能评估的重要手段[1]。由于涉及到热传导和结构热力响应分析,计算效率仍然是焊接过程数值模拟亟待突破的技术难题[2]。
目前,焊接数值模拟方法主要有完全热力耦合法和顺序热力耦合法[3]。顺序热力耦合法假定结构应力场的变化对温度场的影响很小,仅考虑温度场变化对应力场的单向影响,先进行热传导分析获得温度载荷,再进行温度载荷作用下的结构响应分析。相较完全热力耦合法,顺序热力耦合法计算效率高,且计算精度基本相当,目前被广泛采用。但对于复杂工程结构的焊接模拟,顺序热力耦合法的计算效率仍然无法满足需求。

为了提高焊接数值模拟的计算效率并保证计算精度,本文将基于热传导原理,考虑Solid单元和Shell单元特性,采用温度梯度线性约束技术,提出Shell-Solid单元混合建模的方法,结合顺序热力耦合法和双椭球热源模型,建立一种基于Shell-Solid单元混合模型的焊接数值模拟方法,开展不同建模方法的焊接数值模拟和结果对比,以验证混合建模的可行性和有效性。
1 焊接数值模拟方法
焊接数值模拟是一个复杂的非线性问题模拟过程,涉及热传导和结构热力响应等,而数值模拟的精确性则取决于热源模型、单元选取、边界条件设置等因素[10]。本文采用通用有限元软件ABAQUS开展基于单元混合模型的焊接过程数值模拟研究。
1.1 热传导原理
焊接是一个局部急剧升温到高温并随后迅速冷却的过程,在此过程中,温度高度依赖于时间和位置,而材料的性能则随温度的变化而变化。因此,焊接温度场分析是一个典型的非线性瞬态传热问题[11]。传热机制一般可分为3大类:传导、对流和辐射。其中,热传导为:
(1)
式中:Q为热量;A为导热面积;ΔT为不同位置处的温度差;k为材料的导热系数。
热对流采用牛顿冷却为:
(2)
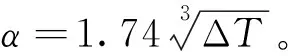
物体通过吸收或辐射的方式进行换热的过程即辐射换热过程,其表达式为:
Q=αr·ΔT·A
(3)
式中αr为辐射换热系数。
1.2 双椭球热源模型
热源的选择也直接影响数值模拟的精度,目前主要有双椭球体热源、高斯表面热源、均布体热源等[11-14]。其中,双椭球体热源是以内部体热源的形式施加到工件上,考虑了电弧热流沿板厚方向的分布,可以更真实反映氩弧焊焊件加热特点,被广泛采用应用于船体钢结构的焊接数值模拟。双椭球体热源在沿焊缝方向上将焊接热能输入划分为前半弧和后半弧2个半椭球,如图1所示[15]。

图1 双椭球热源模型Fig.1 Double ellipsoid heat source model
图1双椭球热源模型中,设定焊接沿X轴方向进行且焊枪电弧垂直于焊缝所在平面,则该热源模型的数学表达式为:
沿X轴方向前半椭球所在空间内一点的热流密度为:
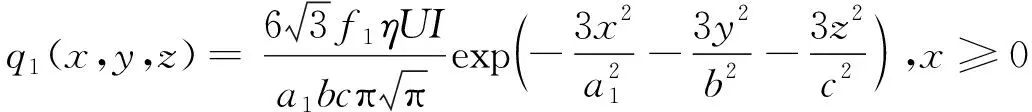
(4)
沿X轴方向后半椭球所在空间内一点的热流密度为:

(5)
式中:q1(x,y,z)、q2(x,y,z)分别为前、后半椭球所在空间内的任意位置的热流密度;a1、a2分别为前、后半椭球的长半轴,其中a1一般取焊缝宽的1/2,a2一般取焊缝宽的2倍;b、c分别代表半椭球的另2个半轴,而且这2个半轴分别相等,根据材料金相检验确定;f1、f2分别为前后椭球热量分配系数,应满足f1+f2=2;η为焊枪热输入效率;U、I为焊接电压、电流。
1.3 Shell-Solid单元混合建模技术
为了在满足计算精度的同时提高计算效率,本文将开展Shell-Solid单元混合建模技术的研究,即焊缝区域及过渡区域采用Solid单元,热影响区使用Shell单元进行模型简化,2种单元连接处力求保证温度和结构变形的连续。通用有限元软件ABAQUS常用的温度场分析单元有8节点线性传热实体单元DC3D8和4节点传热壳单元DS4,结构响应分析单元有8节点C3D8实体单元和4节点S4壳单元等。
Solid单元和Shell单元之间的温度不能连续传递,原因是由于单元的节点温度自由度的空间位置不同。如图2,在热传导分析时,温度分布在节点上,Solid单元温度梯度由NT11表示,而Shell单元一般在其厚度方向设置奇数个积分点,若数目为5个,则其温度梯度有NT11、NT12、NT13、NT14和NT15。

图2 壳与实体温度梯度线性约束Fig.2 Linear constraint of temperature gradient between shell and solid
为了实现2种单元建的温度连续,ABAQUS提供了线性方程约束达到温度的连续传递。线性方程约束可以理解为将不同集中的每一个节点的自由度乘以不同系数构成线性等式结合在一起,其中第1个集可以有一个或多个点或节点,第2个集有且只能有一个点或节点。在壳单元温度自由度与对应位置积分点温度之间建立线性约束,若将实体单元的温度梯度与壳单元的某一梯度相互约束,可以表达为:
Set1:NT11-Set2:NT1n=0 (n=1,2,…)
(6)
式中:Set1、Set2表示不同的集;NT11,NT1n表示不同的温度梯度;Set1:NT11系数为1,Set1:NT1n系数为-1。
1.4 焊接过程数值模拟流程
结合顺序热力耦合法,建立了基于混合模型的焊接数值模拟方法,计算分析流程如图3所示。
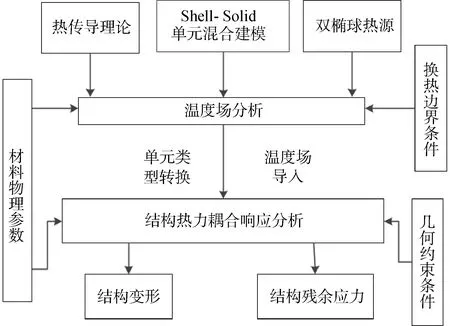
图3 基于Shell-Solid单元混合模型的焊接模拟流程Fig.3 Welding simulation flow based on Shell-Solid element hybrid model
2 焊接过程数值模拟与结果分析
以S350普通低合金钢平板对接焊为例,分别采用Solid模型、Shell模型和混合模型开展了焊接过程的数值模拟,对比分析了3种建模方法的温度场,结构热力耦合响应和计算效率。
2.1 模型与计算参数
模型长400 mm,宽300 mm,高6 mm。焊缝位于宽度中心,模型四边刚固,如图4所示。材料为S350普通低合金钢,材料热物理参数见表1。焊接速率为8 mm/s,焊接效率η取为0.8,热源采用双椭球热源,参数见表2。
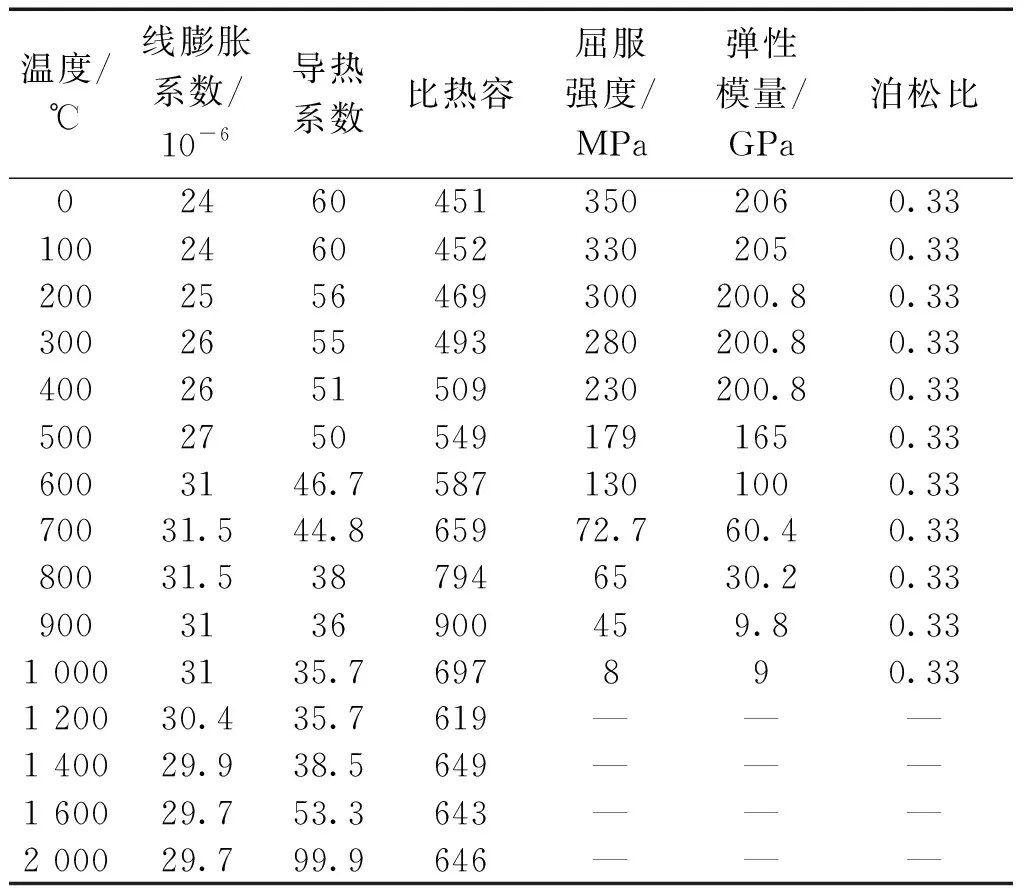
表1 S350普通低合金钢材料性能Table 1 Properties of S350 ordinary low alloy steel

表2 双椭球体热源参数Table 2 Double ellipsoid heat source parameters

图4 模型及应力应变场分析边界Fig.4 Model and stress-strain field analysis boundary
焊缝处网格尺寸取3 mm×2 mm×2 mm,考虑到结构的对称性,只建1/2模型并施加对称边界条件。图5分别为Solid单元模型、Shell单元模型和Shell-Solid单元混合模型。

图5 平板对接焊模型Fig.5 Butt welding model of flat plate
2.2 焊接温度场对比分析
图6分别为Solid模型和混合模型在焊缝中线上、下表面的温度历程。对比计算结果可以发现:焊缝处2个模型各层的温度分布基本一致,上表面的最高温度达到了3 300 ℃,下表面的最高温度也超过了1 500 ℃。因此在焊缝中线两种模型温度吻合良好。

图6 平板焊缝处各点温度历程Fig.6 Temperature history of each point at the plate weld seam
图7为各焊接温度测温点示意图。其中PT1、PT2、PT3在Shell模型及Solid模型中位于一次过渡区域的边缘,PT2′位于二次过渡区域边缘,PT2″位于距离焊缝50 mm处。图8为分别为3种模型PT1、PT2、PT3和PT1′、PT2′、PT3′点温度历程图。

图7 平板对接焊温度测点位置Fig.7 Position of temperature measuring point of flat plate butt welding
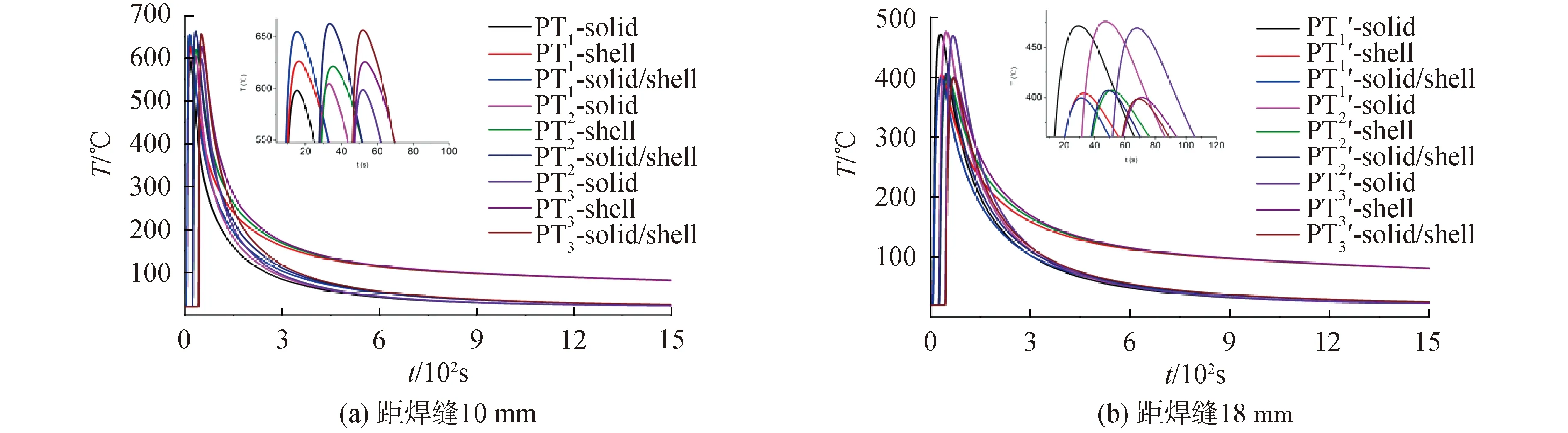
图8 测点温度历程Fig.8 Butt welding temperature history of test points
对比计算结果可以发现:3种模型在距离焊缝10 mm处温度均迅速下降,混合模型温度最高达到660 ℃,Solid模型温度最低但仍在610 ℃,Shell模型温度则维持在630 ℃;solid模型距离焊缝18 mm处温度下降到470 ℃左右,shell模型和混合模型下降到400 ℃左右,距焊缝18 mm处位于shell单元区域,2种单元的差别导致3种模型的温度差异,但总体而言该区域温度相差不大。因此在热影响区域,Shell-Solid单元混合模型在温度分布上与Solid单元模型基本一致。
以焊接电弧经过焊缝上表面B′点为t0时刻,图9分别为3种模型平板横向中线B-B′在不同时刻的温度分布图。对比结果可以发现:

图9 平板对接焊中心线B-B′不同时刻温度分布Fig.9 Temperature distribution at different time of B-B′ of plate center line
1)Solid模型、Shell模型和混合模型均在t=0时刻其温度达到最大值。
2)Solid模型、Shell模型B-B′中心线上各点温度分布及变化趋势基本一致,但最高温度值相差1 200 ℃,相对误差为36.4%;Solid模型与混合模型焊缝区域和远离热影响区温度数值、分布和变化趋势基本一致。
3)混合模型在2种单元混合交界处不同时刻的温度值同Solid模型对比有一定误差。误差分析为由于Solid和Shell 2种单元节点温度积分点空间位置不同,仅依靠约束方程进行温度的强制传递,导致温度传递不平顺,从而带来局部温度曲线不平顺。但混合模型相较Shell模型在焊缝核心区域计算更准确。
因此,采用混合模型进行焊接温度场计算可以获得较好的计算精度。
2.3 焊接应力场对比分析
图10是对接焊3种模型结构在不同焊接模拟方法下的沿X轴方向应力,即纵向应力σx的分布。3种计算模型焊接残余应力分布趋势基本相同,在焊缝处焊接残余应力较大,沿宽度方向由拉应力逐渐转化为压应力;沿纵向两端呈现对称分布。由于采用线性方程约束达到温度的连续传递,混合模型在2类单元连接处的应力分布没有Solid模型和Shell模型均匀,因此建模时要提前做好单元规划。

图10 平板对接焊残余应力σx分布Fig.10 Distribution of residual stress σx in flat butt welding
进一步分析不同模型应力水平,图11为3种模拟方法平板对接焊焊缝上下表面σx的分布图。对比3种方法的纵向残余应力可知:Shell模型纵向残余应力σx,明显小于其他2种方法,而混合模型计算结果在应力数值大小以及分布区域上均与Solid单元结果吻合。各模型σx最大应力值及相对误差见表3。Shell模型与Solid模型两种模拟结果误差18.6%。而混合模型与Solid模型顺序耦合法误差仅2.5%,相比之下混合模型有着显著优势。
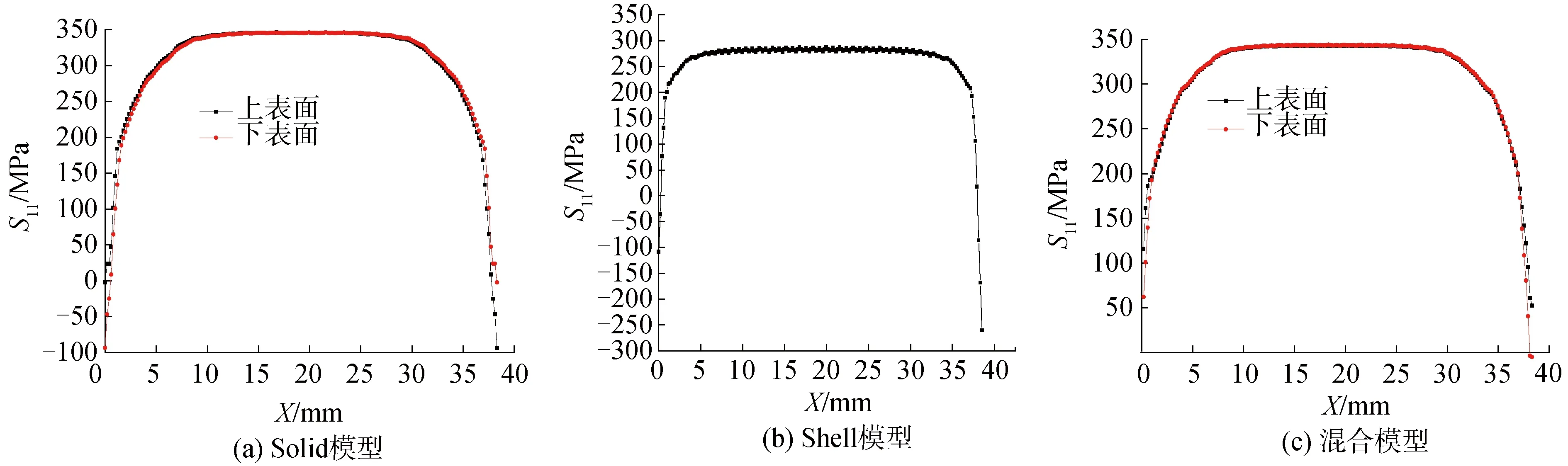
图11 平板对接焊焊缝上下表面应力σx的分布图Fig.11 Stress distribution σx on upper and lower surfaces of flat butt weld
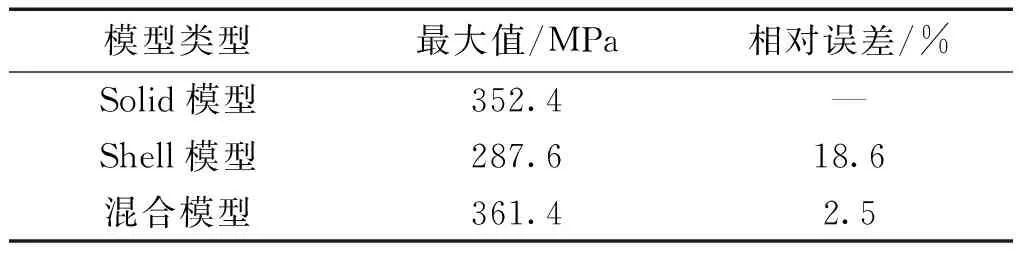
表3 应力σx最大值及相对误差Table 3 maximum stress value and relative error of σx
2.4 计算效率对比分析
表4为Solid模型、Shell模型和混合模型的单元、节点数目以及相关分析步的计算时间。从表中可以看出混合模型能够有效地减少单元和节点数目,进而降低模型自由度,可以有效提高计算效率。

表4 船体板对接焊单元数及计算时间总结Table 4 Summary of hull plate butt welding units and calculation time
结合表3和表4的结果对比,Shell模型相比Solid模型节省46.8%时间,但计算精度误差达到18.6%,准确性有明显不足;而混合模型同样采用顺序耦合法模拟结果与Solid模型仅存在2.5%的误差,且节省28.6%计算时间,在满足计算精度的基础上很大程度上提高了求解速率。
3 结论
1)混合模型的温度场和应力场,与Shell模型和Solid模型基本吻合,尤其是在焊接区域等重点关注区域,与Solid模型结果高度吻合,计算精度较高;
2)相较于Shell模型和Solid模型,混合模型在保证计算精度的前提下,有效地提高了焊接数值模拟的计算效率。
3)采用温度梯度线性约束技术的混合模型焊接数值模拟是可行的,有必要进一步对角接焊等其他焊接形式以及复杂结构开展适用性研究。
