钢筋混凝土矩形空心墩受剪承载力研究
2022-03-11张锡治李星乾章少华丁永君孟祥良王磊
张锡治, 李星乾, 章少华,, 丁永君, 孟祥良, 王磊
(1.天津大学建筑设计规划研究总院有限公司, 天津 300072; 2.天津大学 滨海土木工程结构与安全教育部重点实验室, 天津 300072; 3.天津大学 建筑工程学院, 天津 300072)
桥梁是指跨越障碍(河流或斜坡)的构筑物[1],作为交通运输的枢纽和城市生命线工程的关键组成部分,对保障国家经济社会可持续发展和人民生命财产安全至关重要。现代桥梁结构中,因钢筋混凝土桥墩破坏导致桥梁严重破坏甚至倒塌已成为桥梁震害的重要特征[2]。钢筋混凝土矩形空心墩(简称矩形空心墩)因其制作运输简单、强度/质量比和刚度/质量比大,能够实现桥梁下部结构轻型化、降低基础造价和减小地震作用,在我国西部高烈度地区的桥梁工程中得到了广泛应用[3-4]。
由于截面削弱严重,导致矩形空心墩成为典型的“强弯弱剪”型构件。国内外震害调查表明[5-6],不合理的设计和构造(配筋不足、箍筋失效、纵筋搭接长度不够等)易使矩形空心墩发生脆性剪切破坏,导致其震后修复困难,阻碍震后救援工作开展,严重影响了基础设施系统抗震韧性的实现。我国现行的GB 50111—2006《铁路工程抗震设计规范》[7]、JTG/T 2231-01—2020《公路桥梁抗震设计规范》[8]中均没有对矩形空心墩的抗剪强度计算问题作出特别说明,其设计原则与实心墩保持一致。
为研究矩形空心墩的受剪机理和受剪承载力计算方法,国内外部分学者开展了相关研究并取得了一定成果。Calvi等[9]根据采用不同配筋形式和不同纵筋搭接长度的剪切型矩形空心墩试验结果,提出了矩形空心墩在反复荷载作用下的荷载-位移分段包络线计算方法。Cassese等[10]提出以腹板有效抗剪面积代替全截面面积,利用修正后的UCSD模型[11]计算矩形空心墩受剪承载力,结果表明修正模型的计算精度较原模型有所提高。为准确评估混凝土分量对矩形空心墩受剪承载力的贡献,Shin等[12]设计了13个无箍筋的矩形空心矮墩,基于单调和反复2种不同加载方式研究了各试件受剪性能,建立了以剪跨比、实心截面纵筋配筋率和位移延性系数为变量的矩形空心墩受剪承载力计算模型。鉴于矩形薄壁空心墩在我国公路、铁路桥梁工程中应用广泛,孙治国等[13-14]对2个试件分别进行了定轴力和变轴力低周反复加载试验,对比分析了已有受剪承载力计算模型对矩形薄壁空心墩的适用性。
目前,国内外规范大多直接采用实心墩受剪计算模型分析矩形空心墩受剪承载力,其合理性和准确性有待进一步研究。此外,现代桥梁结构向大跨、高耸、重载和承受恶劣环境方向的发展趋势推动了高强材料的应用,而对采用高强材料(如高强混凝土、高强钢筋等)的矩形空心墩受剪承载力计算方法研究较少。为分析实心墩模型对矩形空心墩受剪承载力计算的适用性,尤其是对采用高强混凝土和高强箍筋矩形空心墩的适用性,本文基于桁架-拱模型建立考虑位移延性需求的矩形空心墩受剪承载力计算模型,通过从国内外文献中收集的共22组矩形空心墩受剪试验数据,对比分析本文模型和已有模型对矩形空心墩受剪承载力计算的适用性、有效性和准确性。
1 基于桁架-拱模型的矩形空心墩受剪承载力
1.1 矩形空心墩受剪试验数据
为确定桁架-拱模型中的关键参数取值,建立合理的矩形空心墩受剪承载力计算模型,从国内外文献[9, 10, 14-20]中收集了22组矩形空心墩在单调和反复荷载作用下的受剪试验数据。混凝土强度换算f′c=αfcu,k,f′c为混凝土圆柱体轴心抗压强度,fcu,k为混凝土立方体抗压强度标准值,对C60以下混凝土α=0.790,C70混凝土α=0.857,C80混凝土α=0.875[21];位移延性系数μ=Δu/Δy,其中Δu为极限位移,取水平荷载下降至峰值荷载的80%时对应的水平位移,Δy为名义屈服位移。
1.2 桁架机构
对以剪切变形为主的矩形空心墩,其腹板出现斜裂缝后,斜裂缝间混凝土块体可视为斜压杆,与斜裂缝相交的箍筋将混凝土块体连接成整体,两者协同工作实现剪力桁架式传递[20]。在桁架机构中,纵向受拉钢筋为上弦拉杆,纵向受压钢筋及剪压区受压混凝土为下弦压杆,箍筋为斜拉腹杆,混凝土为斜压腹杆,如图1(a)所示,桁架机构计算简图如图1(b)所示。

图1 桁架机构Fig.1 Truss model
图1中he为截面有效高度,定义为截面受拉纵筋合力点到受压区边缘的距离,近似取he=0.9h,h为截面高度;T为纵筋拉力;c为纵筋或混凝土压力;φ为混凝土斜压杆倾角;α为箍筋与纵轴间夹角;σc为混凝土压应力。
取图1(b)的左侧隔离体为分析对象,隔离体受力如图2(a)所示。根据静力平衡条件可求得桁架机构受剪承载力Vt为:
(1)
式中:Asv为截面各肢箍筋总面积;σsv为箍筋应力;s为箍筋间距。
高强箍筋的约束作用可以提高矩形空心墩的承载能力和变形性能,改善高强混凝土的脆性,近年来在桥梁结构中得到了广泛应用。通常,在进行矩形空心墩设计时,假定其受剪破坏时箍筋屈服强度能够得到充分发挥,即在计算受剪承载力时,箍筋应力σsv统一取屈服强度fyv。而实际上,当矩形空心墩采用高强箍筋,其受剪破坏时箍筋可能无法达到屈服强度,直接采用屈服强度进行计算高估了箍筋分量受剪承载力。
根据近年来国内外对高强箍筋钢筋混凝土柱进行的受剪试验[22-23]结果,在达到承载力极限状态时,箍筋应力值取决于平均约束应力ρsvfyv,其上限值为3.5[24],ρsv为配箍率。当平均约束应力低于该上限值时,箍筋应力取箍筋屈服强度。因此,箍筋应力σsv为:
σsv=min(fyv,3.5/ρsv)
(2)
以图1(b)桁架机构的右侧隔离体(图2(b))为分析对象,根据箍筋拉力、纵筋拉力和混凝土斜压力的平衡条件可得:
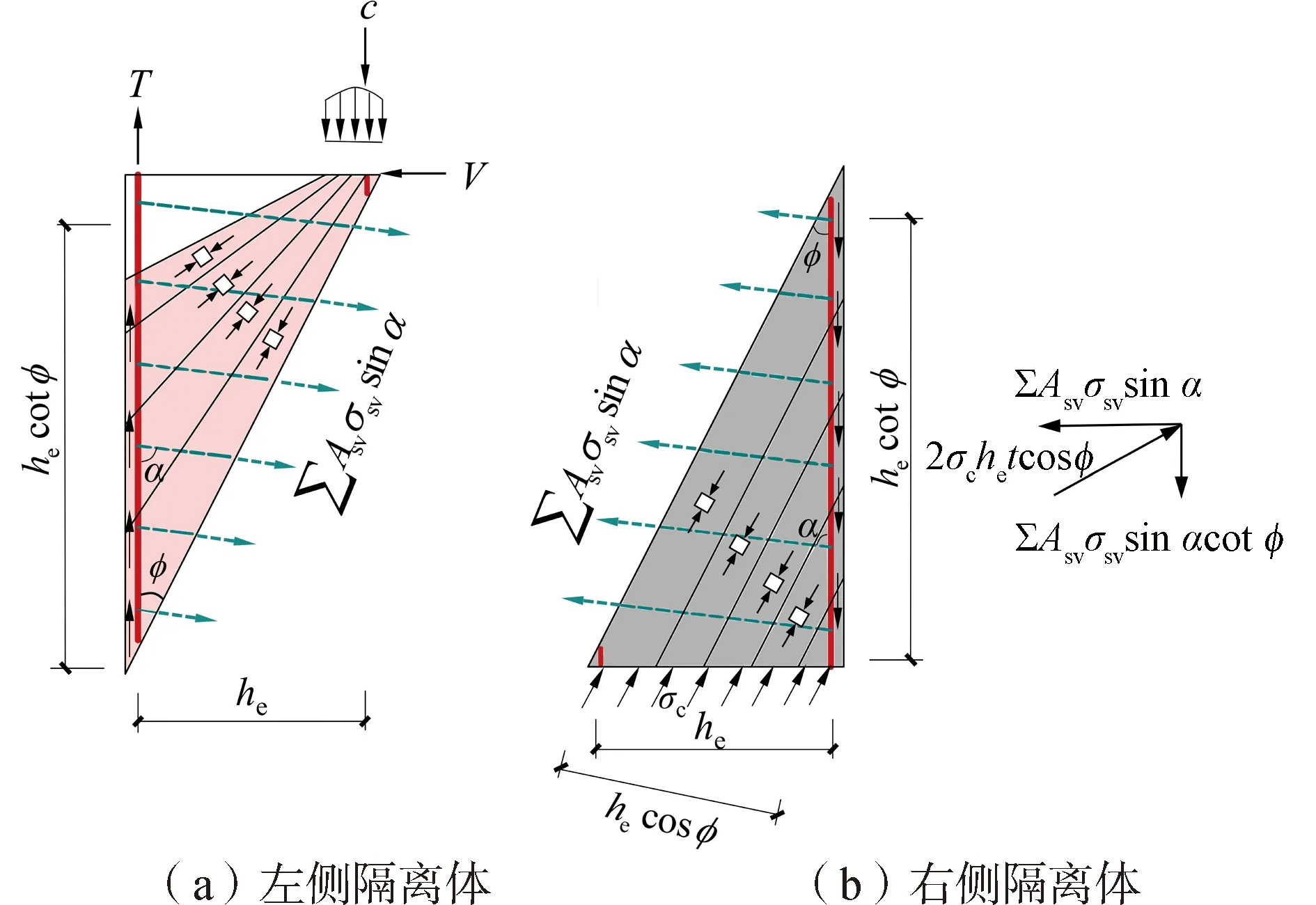
图2 桁架机构隔离体受力示意Fig.2 Schematic diagram of isolators of truss model
(∑Asvσsvsinα)2(1+cot2φ)=(2σchetcosφ)2
(3)
式中t为壁厚,取最薄处的壁厚值。
(4)
由于混凝土是一种各向异性的非线性弹塑性材料,斜裂缝的产生会造成混凝土抗压强度降低,使混凝土在双向拉压状态下出现软化现象,混凝土强度愈高,软化现象愈显著。为避免直接采用混凝土抗压强度而过高估计混凝土的抗剪能力,一般通过引入软化系数v降低混凝土压应力σc进行受剪分析,即:
σc=vfc
(5)
式中fc为混凝土轴心抗压强度。
目前,国内外学者对混凝土软化系数的取值已进行了大量研究,提出了不同形式的软化系数表达式。日本设计指南中假定钢筋和混凝土为理想弹塑性材料,忽略变形协调条件,提出软化系数v=0.7-fc/200。与日本设计指南的软化系数表达式类似,文献[24]建议统计试验数据时取v=1.0-fc/133。上述计算公式中,软化系数与混凝土强度均为线性关系,而文献[25]指出,软化系数与混凝土强度呈非线性关系,通过对不同强度等级混凝土的软化系数进行回归分析,提出混凝土软化系数统一表达式:
(6)
为准确反映不同混凝土强度等级和不同箍筋强度等级矩形空心墩的受剪软化规律,根据文献[25]提出的软化系数与混凝土强度非线性关系表达式,考虑斜裂缝混凝土有效抗压强度离散性随混凝土强度的提高而增大,并考虑国内外材料的差异性,结合文献[24]中混凝土软化系数取值,建议混凝土软化系数表达式为:
(7)
为确保混凝土斜裂缝区域压应力有效传递,取cotφ=2为上限[26],将式(7)代入式(4),则式(4)应改写为:
(8)
将式(8)代入式(1),得到桁架机构受剪承载力Vt为:
(9)
1.3 拱机构
拱机构作用存在于构件整个受力过程中,实际拱机构剪力传递机制如图3(a)所示:混凝土视为斜压杆,中部膨胀部分为拱压应力扩散区域。将图3(a)简化为图3(b)所示模型,则拱机构受剪承载力Va为:
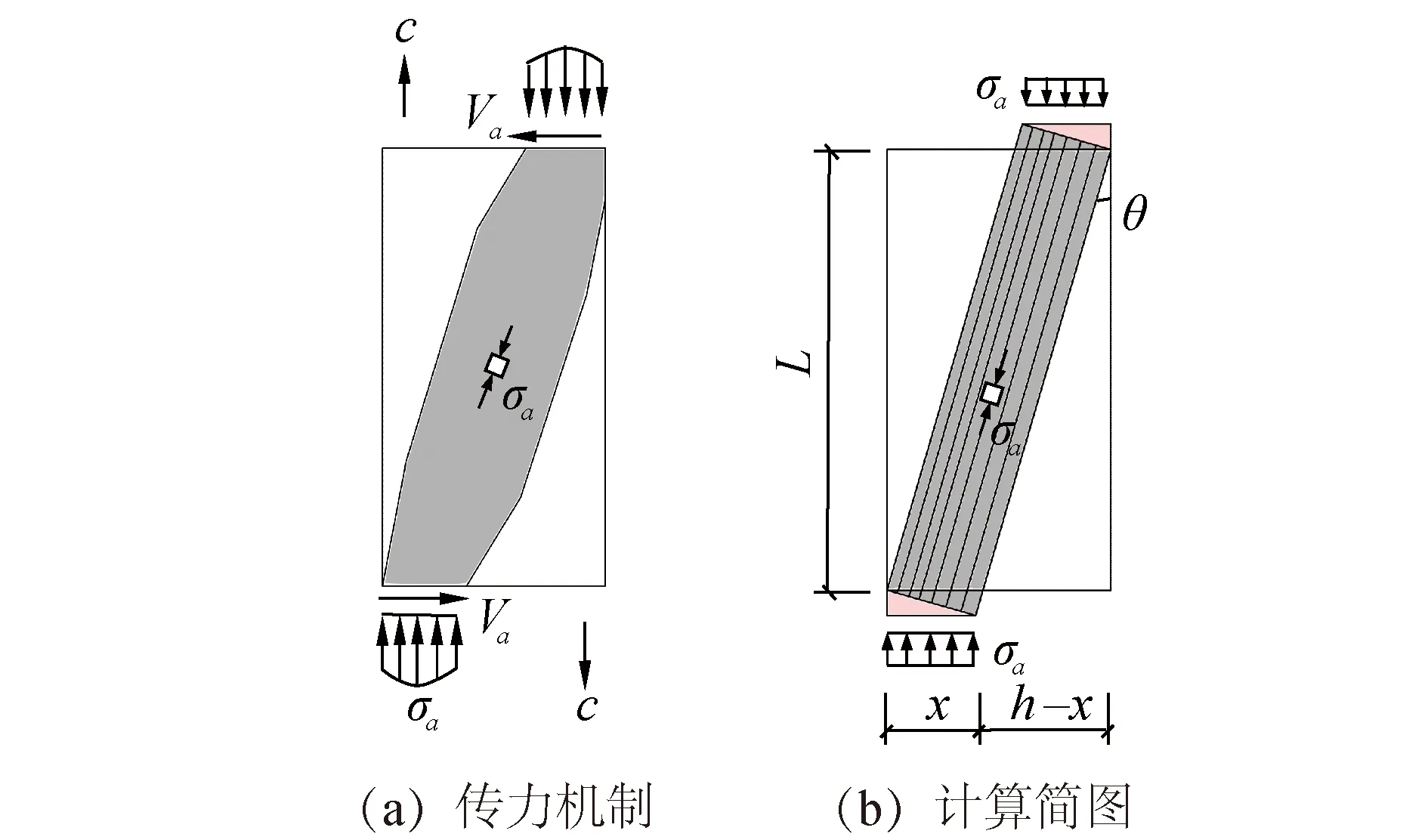
图3 拱机构受力示意Fig.3 Schematic diagram of arch model
Va=2σat(x-ct)tanθ
(10)
式中:σa为拱机构中的混凝土压应力;ct为混凝土保护层厚度;x为受压区混凝土高度,按文献[27]建议方法计算,x=[0.25+0.85N/(f′cAg)]h,N为试验轴压力,Ag为截面面积。
桁架机构作用与剪跨比呈正相关,拱机构作用与剪跨比呈负相关,采用以下基本假定[28]:1)对于轴力N=0,当剪跨比λ<0.5时,只考虑拱作用;当λ>3.0时,只考虑桁架作用;2)对于轴力N0,由拱机构传递全部轴力。
根据以上基本假定,当轴力N=0时,拱机构中的混凝土压应力按下列方法确定:
1)当λ<0.5时,剪力由拱机构传递,σa1=vfc;
2)当λ>3.0时,剪力由桁架机构传递,σa1=0;
3)当0.5≤λ≤3.0时,压应力按线性插值计算,σa1=(1.2-0.4λ)vfc;
当轴力N0时,全部轴力由拱机构传递,拱机构中的混凝土压应力:
σa2=N/(bx)
(11)
因此,拱机构中的混凝土压应力σa为:
σa=σa1+σa2=(1.2-0.4λ)vfc+N/(bx)
(12)
将式(12)代入式(10),可得拱机构受剪承载力Va为:
(13)
式中b为矩形空心墩截面宽度。
2 矩形空心墩受剪承载力计算
2.1 受剪承载力
矩形空心墩受剪承载力等于桁架机构和拱机构的受剪承载力之和,故矩形空心墩受剪承载力V为:
V=Vt+Va
(14)
将式(9)、(13)代入式(14),可得矩形空心墩受剪承载力表达式为:
V=Vt+Va=

(15)
2.2 考虑位移延性需求的受剪承载力计算模型
反复荷载作用下,混凝土裂缝的出现(时间序列特征)和发展(空间序列特征)均明显快于单调荷载作用,且随着裂缝的空间扩散和程度加深,混凝土骨料咬合力和粘结力下降,软化作用使混凝土有效抗压强度减小,导致混凝土分量的受剪承载力降低。此外,根据国内外桥墩设计规范,为确保矩形空心墩的受力性能,通常采用双层对称配筋构型,同时设置大量横向联系钢筋,但在反复荷载作用下,箍筋失效仍难以避免,导致箍筋分量的受剪承载力降低。式(15)未考虑反复荷载作用下混凝土、箍筋分量受剪承载力的降低影响,高估了矩形空心墩在地震作用下的受剪承载力。
为准确量化评估反复荷载作用对混凝土和箍筋分量受剪承载力的影响,美国加州应用技术委员会[29](Applied Technology Council, ATC)提出一种受剪承载力与位移延性系数相关联的概念模型,以反映受剪切变形影响较大的钢筋混凝土柱受剪承载力随变形能力增大而降低的影响,如图4所示[28]。该模型采用位移延性系数表征受剪需求,构件的受剪承载力随位移延性系数的增大逐渐降低,阐明了桥墩延性抗震设计与抗剪能力保护设计原则之间的关系。
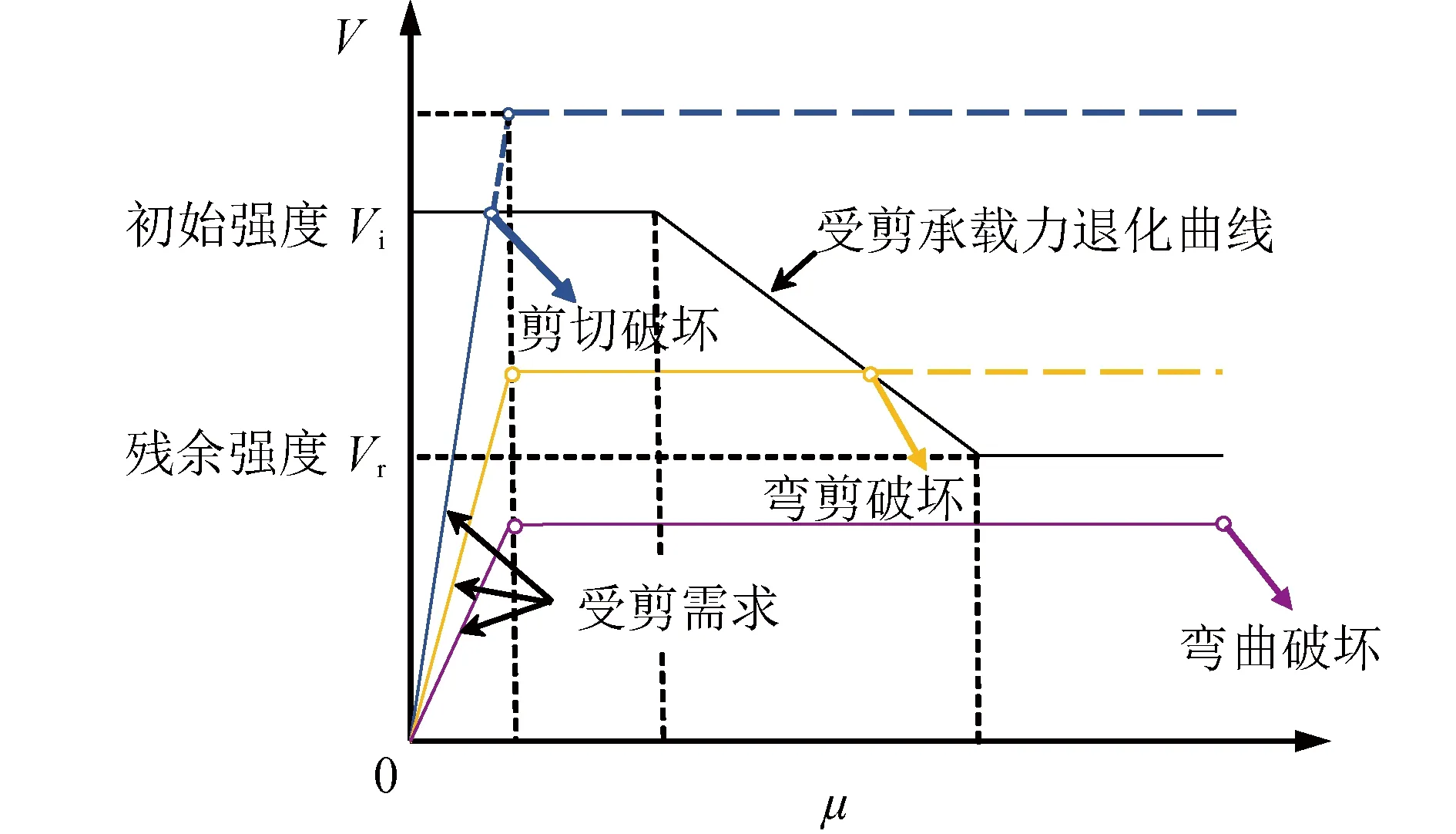
图4 ATC模型Fig.4 ATC model
借鉴ATC模型的受剪承载力退化曲线,本文采用受剪承载力分段折减系数γ反映反复荷载作用下混凝土软化和箍筋失效对矩形空心墩受剪承载力降低的影响,γ与位移延性系数μ之间的关系如图5所示,其表达式为:
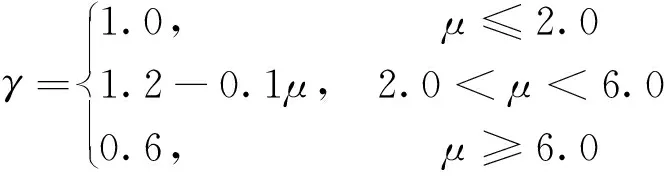
(16)
为验证γ取值的合理性,根据本文收集的反复荷载作用下14组矩形空心墩受剪试验数据,采用不考虑位移延性需求的式(15)计算得到各试件的受剪承载力Vc1,Ve/Vc1与位移延性系数的关系如图5所示。由于Vc1在不同位移延性系数下始终为恒值,而Ve和Ve/Vc1随位移延性系数增大而减小,故Ve/Vc1与位移延性系数的关系反映了反复荷载作用对矩形空心墩受剪承载力降低的影响,即Ve/Vc1与γ的作用相同。由图5可知,折减系数γ计算曲线可以较好地包络试验数据,能够较好地反映试件受剪承载力随位移延性系数增大而降低的特性。需要说明的是,随着试验数据的不断积累,所提出的折减系数曲线的合理性可以得到进一步验证。

图5 受剪承载力折减系数Fig.5 Reduction coefficient of shear strength
因此,考虑位移延性需求的矩形空心墩受剪承载力V为:
V=γ(Vt+Va)=

(17)
对单调加载的矩形空心墩受剪承载力计算而言,当γ=1.0时,式(17)与式(14)相同,故式(17)同时适用于单调和反复荷载作用下的矩形空心墩受剪承载力计算。
3 矩形空心墩受剪承载力计算模型对比分析
3.1 已有受剪承载力计算模型
目前计算矩形空心墩受剪承载力时基本沿用实心墩计算模型。为分析已有实心墩模型对矩形空心墩受剪承载力计算的适用性,结合Priestley等[30]、Aschheim[31]、Sezen等[32]、Kowalsky等[11]和我国JGJ/T 2231-01—2020《公路桥梁抗震设计规范》[8]给出的实心墩受剪承载力计算模型,以及Shin等[12]提出的矩形空心墩受剪承载力计算模型,对22组矩形空心墩试件的受剪承载力进行分析。
上述计算模型中,Priestley模型受剪承载力由混凝土分量、箍筋分量和轴压力分量3部分组成,其余模型均由混凝土分量和箍筋分量组成。除Kowalsky模型外,其余模型均考虑轴力对受剪承载力提高的有利作用。Sezen模型中同时考虑了位移延性需求对混凝土和箍筋分量受剪承载力的折减,其余模型均仅考虑其对混凝土分量受剪承载力的影响。
3.2 矩形空心墩受剪承载力计算模型对比分析
基于从国内外文献中收集的矩形空心墩受剪试验数据,采用已有的受剪计算模型和本文提出的计算模型确定各组试件的受剪承载力,对比分析各模型的适用性、有效性和准确性。
各模型计算结果与混凝土强度关系如图6所示。由图6(a)~(d)、(f)可知:1)Priestley模型、Aschheim模型和Sezen模型计算的矩形空心墩受剪承载力明显偏高,其理论值与试验值之比Vcal/Ve的平均值分别为1.31、1.20和1.20,变异系数分别为0.193、0.266和0.098;Sezen模型具有较好的计算稳定性,Aschheim模型计算结果的变异系数较大,计算准确性和稳定性均不理想;2)Kowalsky模型计算得到的Vcal/Ve平均值为0.75,变异系数为0.177,JGJ/T 2231-01—2020模型计算得到的Vcal/Ve平均值为0.39,变异系数为0.109,2个模型的计算值与试验值之比明显偏低,但变异系数不大,用于工程设计时具有较大的安全度。

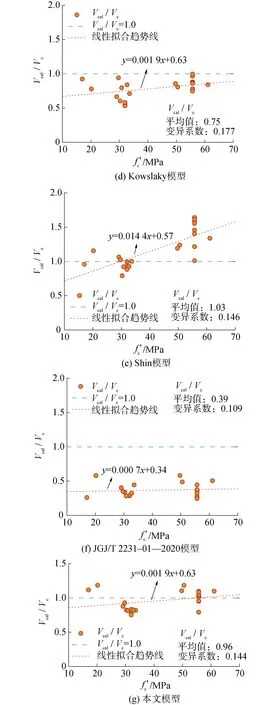
图6 不同混凝土强度下各模型受剪承载力计算结果Fig.6 The calculation results of shear strength model under different concrete strength
Shin等[12]借鉴Kowalsky模型的表达形式,考虑轴压力影响,并以实心截面纵筋配筋率ρsolid代替实际空心截面纵筋配筋率ρl,提出了适用于矩形空心墩的受剪计算模型。该模型计算得到的Vcal/Ve平均值为1.03,变异系数为0.146。由图6(e)可知,Shin模型对普通强度混凝土矩形空心墩的受剪承载力计算误差较小且偏于保守,但计算高强混凝土矩形空心墩受剪承载力时偏于不安全。根据线性拟合趋势线可知,随着混凝土强度的提高,其计算结果与试验结果的比值迅速增大,表明Shin模型对不同混凝土强度等级矩形空心墩受剪承载力计算的适用性较差。
利用试验数据对本文提出的矩形空心墩受剪承载力计算模型的准确性进行分析,其理论值与试验值之比Vcal/Ve的平均值为0.96,变异系数为0.144。由图6(g)可以看出,本文模型对不同混凝土强度等级矩形空心墩的受剪承载力具有较好的适用性,但略高估了部分混凝土强度较低(f′c<20 MPa)和较高(f′c>50 MPa)矩形空心墩的受剪承载力。需要指出的是,当f′c>60 MPa时本文模型可能给出偏于不安全的计算结果,如图6(g)线性拟合趋势线所示。
各模型计算结果与箍筋强度关系如图7所示。
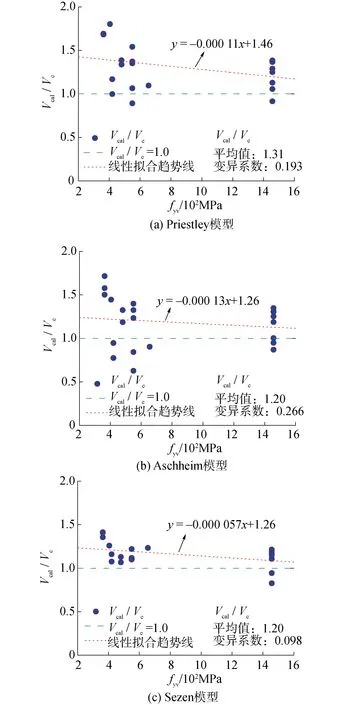
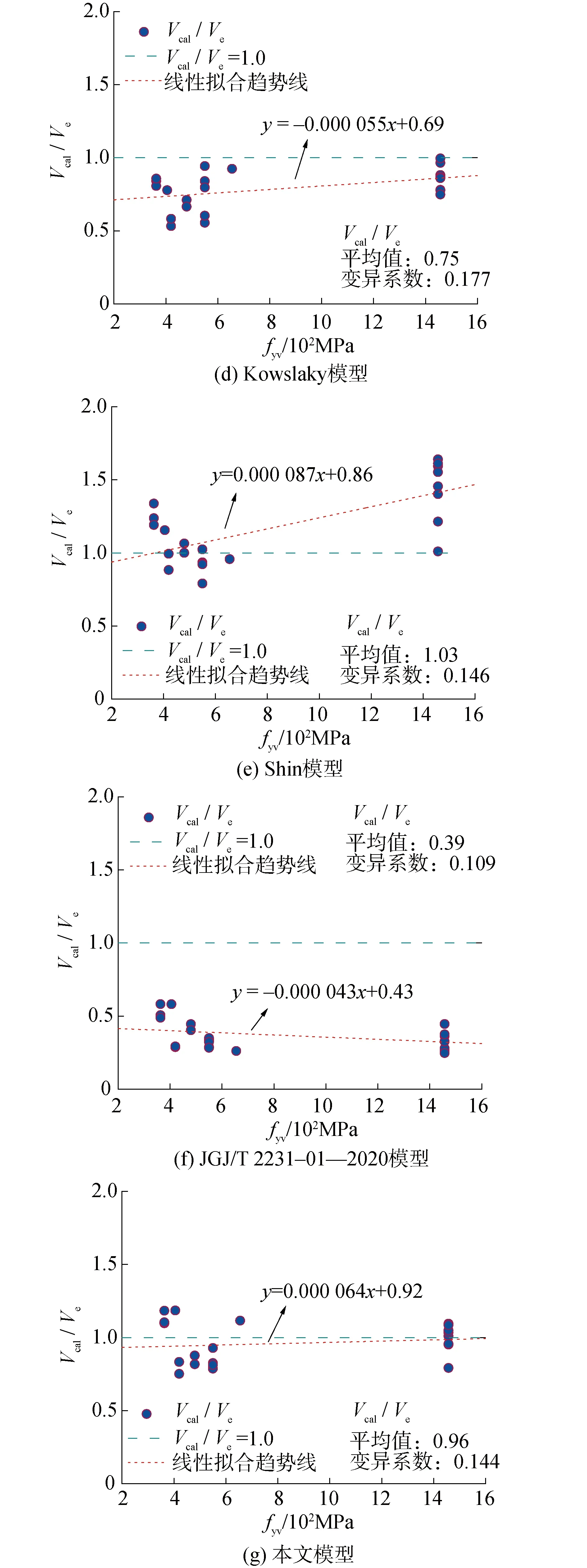
图7 不同箍筋强度下各模型受剪承载力计算结果Fig.7 The calculation results of shear strength model under different stirrups strength
由图可知:1)Priestley模型、Aschheim模型和Sezen模型均高估了普通强度箍筋矩形空心墩的受剪承载力,随着箍筋强度的增加,计算准确性有所提高;2)Kowalsky模型和JGJ/T 2231-01—2020模型对不同箍筋强度等级矩形空心墩的受剪承载力计算均较为保守。随着箍筋强度的增加,Kowalsky模型计算结果愈接近试验值,JGJ/T 2231-01—2020模型计算结果愈偏于安全;3)Shin模型无论对普通还是高强箍筋矩形空心墩受剪承载力计算均具有较大的离散性,且箍筋强度越高其离散性越大;4)本文模型能较为准确地计算不同箍筋强度等级矩形空心墩的受剪承载力,且计算准确性随箍筋强度的增大而提高。
为进一步验证本文模型的有效性和准确性,以位移延性系数、剪跨比和轴压比为变量对其计算结果进行分析,如图8~10所示。
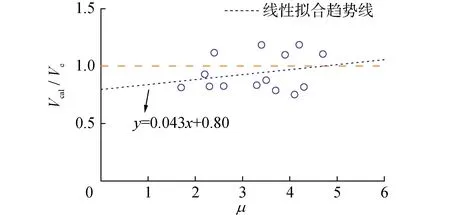
图8 不同位移延性系数下本文模型验证Fig.8 Verification of proposed shear strength model for different displacement ductility factor
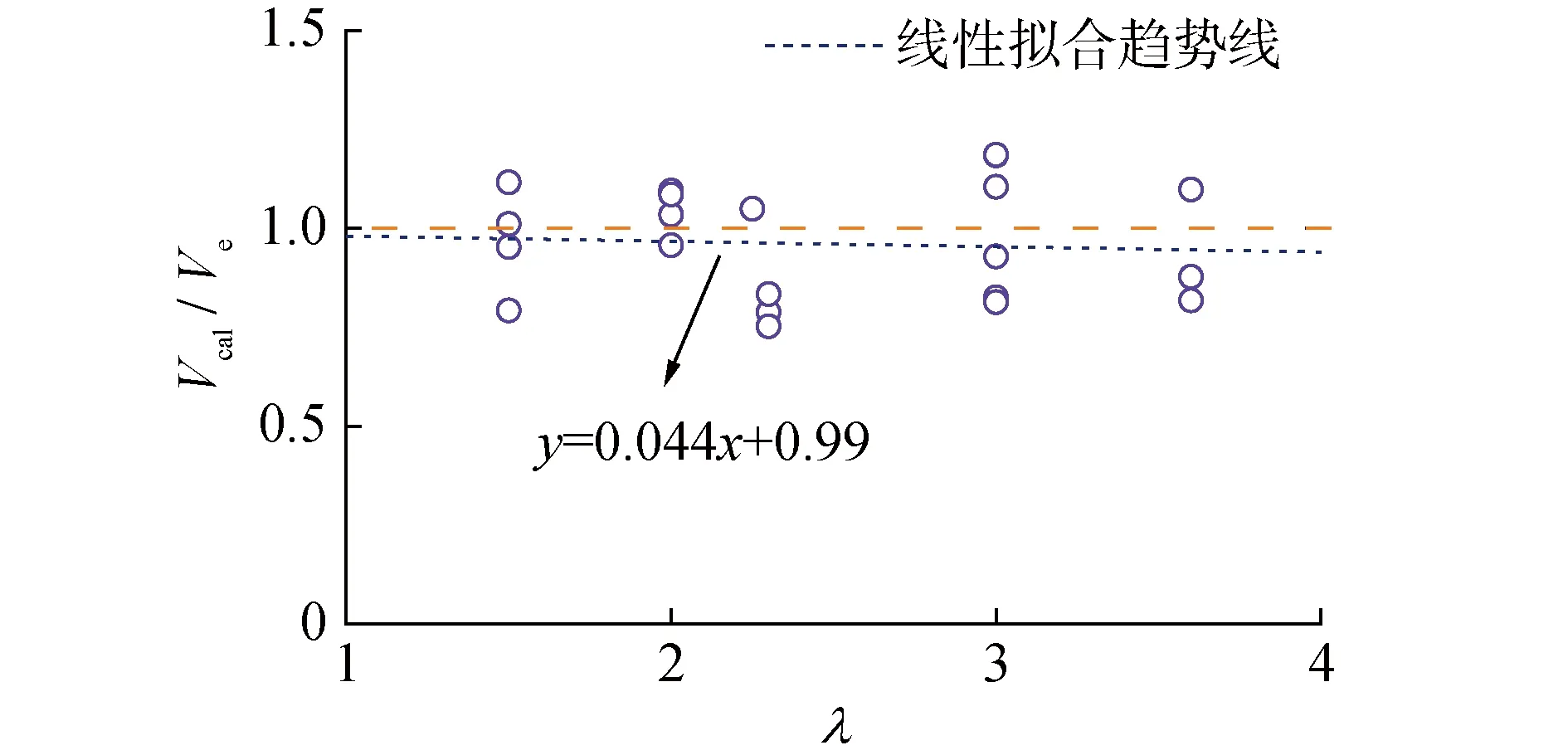
图9 不同剪跨比下本文模型验证Fig.9 Verification of proposed shear strength model for different shear span ratio
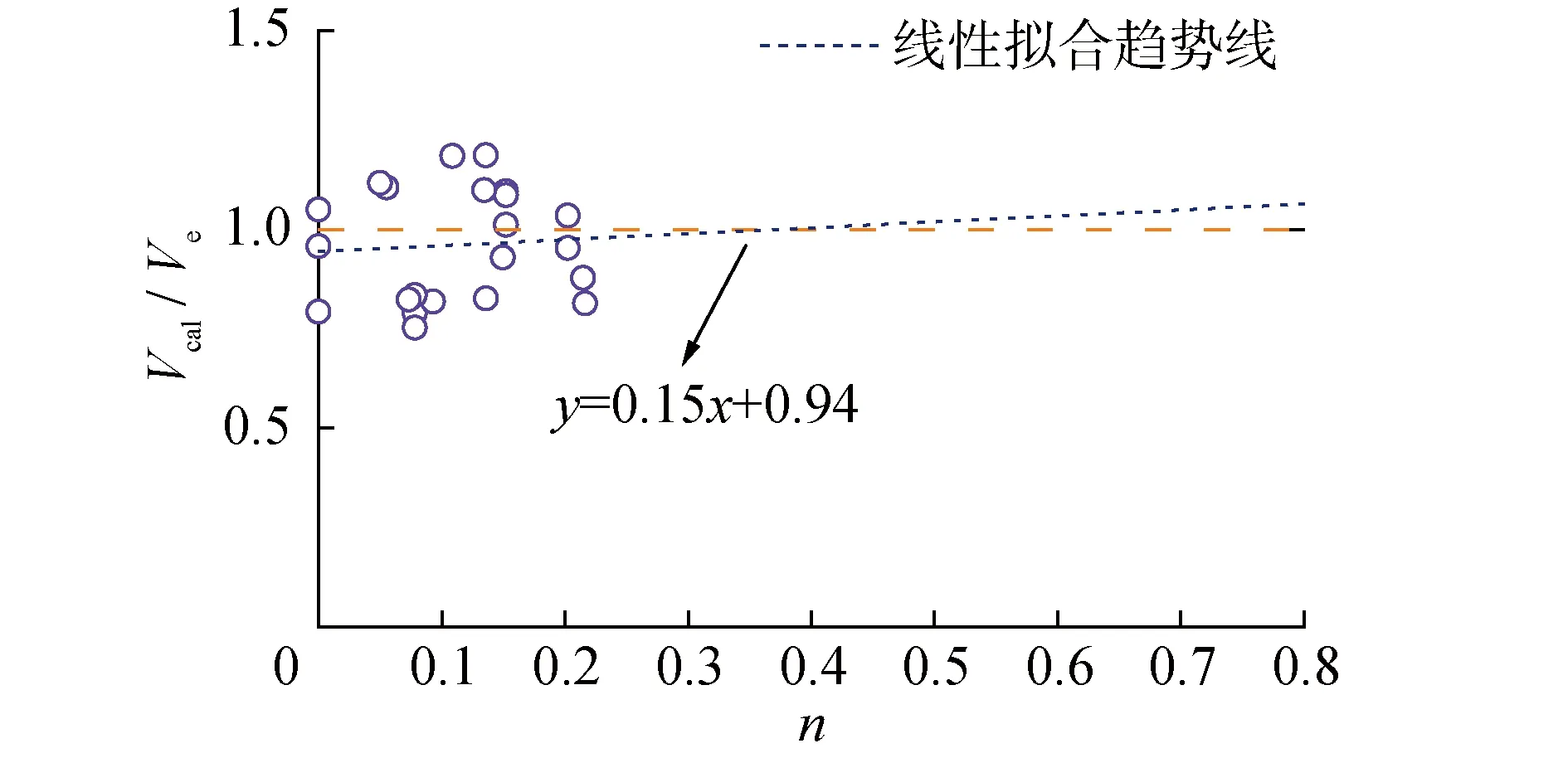
图10 不同轴压比下本文模型验证Fig.10 Verification of proposed shear strength model for different axial compression ratio
由图可知,本文模型能够较为准确地计算不同变量下的矩形空心墩受剪承载力,且计算值与试验值之比的离散性较小。此外,选用文献[9,10,14-19]和文献[20]试验数据分析本文模型对采用不同加载方式矩形空心墩受剪承载力计算的适用性,其计算值与试验值的对比如图11所示。对单调受剪试件而言,本文模型计算得到的Vcal/Ve平均值为0.997,均方差为0.008,变异系数为0.092。除无轴力试件HPCT1外,其余试件受剪承载力计算值与试验值误差均在10%以内;对反复受剪试件而言,Vcal/Ve平均值为0.939,均方差为0.024,变异系数为0.165,计算结果与试验结果均吻合较好。
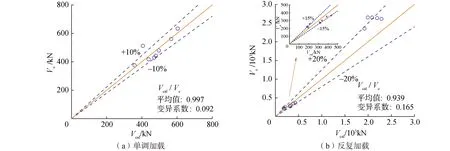
图11 不同加载方式下本文模型验证Fig.11 Verification of proposed shear strength model for different loading process
4 结论
1)基于桁架-拱模型,考虑箍筋与纵轴间夹角、软化系数与混凝土强度间非线性关系等因素影响,确定高强箍筋平均约束应力上限值为3.5,建立了考虑位移延性需求的矩形空心墩受剪承载力计算模型。分析验证发现,该模型对计算不同混凝土强度等级和不同箍筋强度等级矩形空心墩的受剪承载力具有较好的适用性。当f′c<60 MPa且fyv<1 600 MPa时,计算准确性随混凝土和箍筋强度的增大而提高。
2)Priestley模型、Aschheim模型和Sezen模型均高估了矩形空心墩的受剪承载力;Kowalsky模型和JTG/T 2231-01-2020模型的计算结果偏于保守,用于工程设计时具有较大的安全度;Shin模型能较为准确地计算普通强度混凝土矩形空心墩的受剪承载力,但对高强混凝土矩形空心墩的计算结果偏于不安全,不同箍筋强度下计算结果的离散性较大。
3)本文模型计算值与试验值之比的离散性受位移延性系数、剪跨比、轴压比和加载方式等变量影响较小,可用于矩形空心墩受剪承载力计算和分析。
