基于逆子结构分析方法的车门振动噪声分析

黄 河

（湖南财经工业职业技术学院 汽车工程系，湖南 衡阳421002）

随着汽车制造技术水平不断提高，人们对汽车整车各种性能要求越来越高，其中噪声振动水平更能直观体现汽车舒适性性能，成为影响顾客选购车型时重要参考因素。根据相关数据统计，一款新车的研发生产过程中，对整车NVH（N-噪声、V-振动、H-舒适性）投入技术和研发经费占整体研发费用20%[1]，所以汽车噪声和振动控制技术显得越来越重要。

Janssens 等[2]基于参数加载模型提出了扩展工况传递路径分析方法（OPAX），莫愁等[3]对OPAX 方法进行改进，提高了计算精度和运算效率。阿拉巴马大学的Liu[4]在其学位论文中阐述逆子结构传递路径理论公式推导过程，并通过实车试验验证此方法有效性。邓支强[5]在其学位论文中利用逆子结构传递路径分析方法找出振动能量关键传递路径，解决某款轻型卡车的驾驶室振动过于严重问题。同时也验证该方法相比于其他传递路径分析方法效率提高约50%，且误差满足精度要求。

本文研究背景是某款SUV以11 km/h～13 km/h行驶在搓衣板路面上时，左后门出现异常振动现象。由于汽车振动系统极其复杂，因此借助逆子结构分析方法根据振动能量的传递路径进行分析。该技术可以在底盘系统与车身系统耦合状态下即在无需从整体系统中拆离振动源的条件下，通过试验测量系统水平频率响应函数(FRF)，采用相应算法[6]反求出耦合界面的连接元件动刚度、非耦合子结构响应FRF、激励传递率，从而找出路径贡献量。通过优化贡献量较大传递路径的动态传递特性，使得车门振动幅值被控制在预定的目标之内。

1 二级多点耦合逆子结构理论

图1 中频率响应函数HA,o(a)c(a)j和HB,c(b)ji(b)分别表示自由状态下子结构A、B的激励Fi(a)、Fi(b)与目标响应Xo(a)、Xc(b)能量传递关系。子结构A、B通过连接元件耦合在一起，组合成多点刚柔耦合二级子结构系统如图2所示。

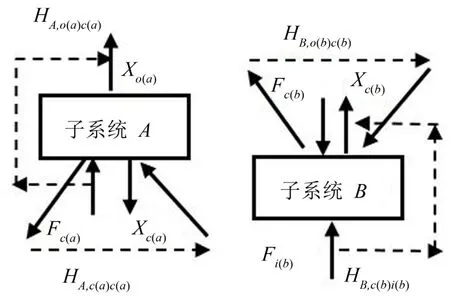
图1 自由状态子结构A、B的输入、输出关系

图2 耦合状态下二级子结构输入、输出关系

图1 中子结构水平频率响应函数与图2 中系统级水平频率响应函数HS,o(a)i(b)等价关系公式[7-8]如下：

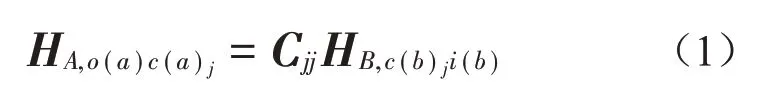
其中：

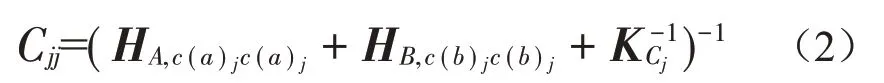
式中：下标j、A、B、S分别表示系统耦合界面接附点自由度坐标、自由状态下子结构A和B、耦合连接一起的整体系统。i(b)、o(a)、c(a)、c(b)分别表示作用在子结构B（底盘系统）上的自由度i向激励、目标响应点（后车门）输出自由度、子结构A（被动端）耦合处接附点输出自由度、子结构B（主动端）耦合处接附点输出自由度，K(c)表示连接元件的动刚度。Cjj表示整车振动耦合系统综合动刚度，由连接元件动刚度K(c)和主、被动端接附点原点导纳3部分组成。

根据多点耦合二级逆子结构理论得知，在自由状态下主、被动端接附点原点在自由度j向上的FRF即HB,c(b)jc(b)j、HA,c(a)jc(a)j以及连接元件动刚度K(c)由相应测量系统级水平FRF[4]计算求得。

同时在自由度j上，子结构A目标响应点振动灵敏度HA,o(a)c(a)j以及路面激励的振动传递激励灵敏度HB,c(b)ji(b)由耦合状态下的系统级FRF[4]计算求得。

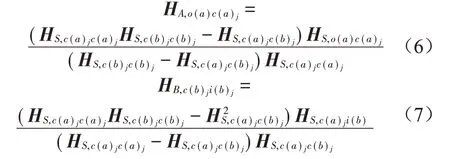
式（3）～式（7）中等号左边所有系统水平的频响函数都是在不拆除激励源情况下由试验直接测量得到。采用逆子结构传递路径方法实现了通过利用直接测量所得的系统级水平的频响函数，反求非耦合状态下子结构部件水平的频响函数以及耦合界面连接元件的动刚度特性，与传统TPA方法相比较，本文所提方法工作效率提高50%；与OPTA 方法精度相当[9－10]。

2 实车分析

如图3 至图4 所示，针对某款SUV 以11 km/h～13 km/h行驶在搓衣板路面上时，左后车门出现异常振动现象进行研究。前期经过鹅卵石、搓衣板路上多次实车测试，发现只有在搓衣板路面上在23.8 Hz时左后门目标测试响应点加速度峰值为7 663 mm/s2，相对称右后门响应位置测试点的加速度峰值为3 656 mm/s2，因此下一步对来自搓衣板路面激励产生的振动传递路径进行分析。

图3 搓衣板路面

图4 传感器安装位置

2.1 建立车辆系统分析模型

为了方便研究将整车振动系统划分为子结构A、B两部分：车轮、副车架结构、减震装置等结构归类为子结构B，车身、车身内饰件系统归类为子结构A，如图5所示。

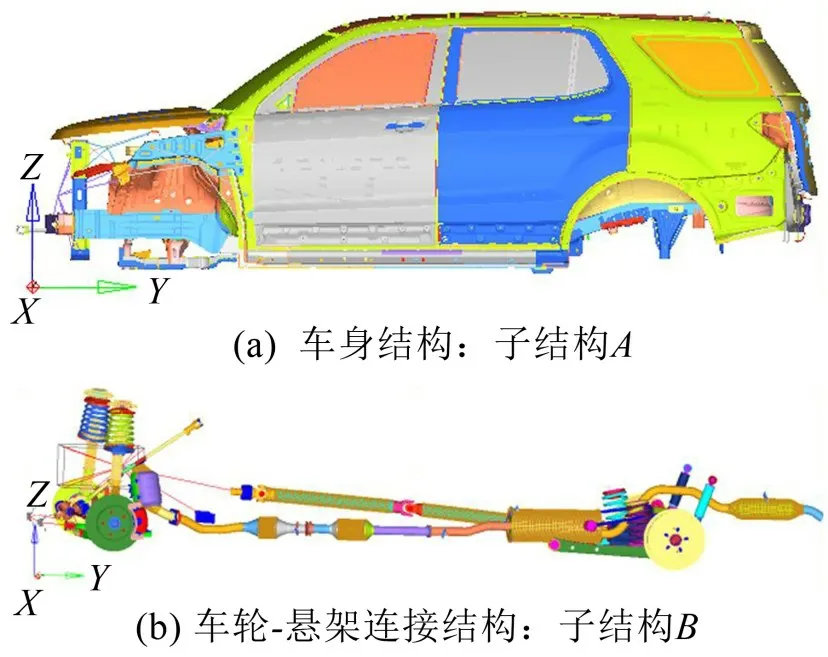
图5 整车系统模型

两子结构之间通过多个不同参数阻尼-弹性元件连接耦合在一起，且子结构A、B之间的耦合界面接附点是有限、离散的。由图6可知，整车前部分通过2 个左、右控制臂以及2 个减震器连接耦合在一起，编号1～6为连接耦合处接附点。整车后半部分通过2根纵向推力杆、2根拉力杆、2个减震器、2个螺旋弹簧连接元件以及1 根后横向稳定杆连接、耦合在一起，相对应编号7～15 为耦合处接附点。因此车身系统和底盘系统耦合界面共有15个接附点，每个接附点包括3 个平动自由度坐标，共有45 个平动耦合坐标自由度。由于转动方向的激励对耦合动态特性影响极小，本文不予考虑。

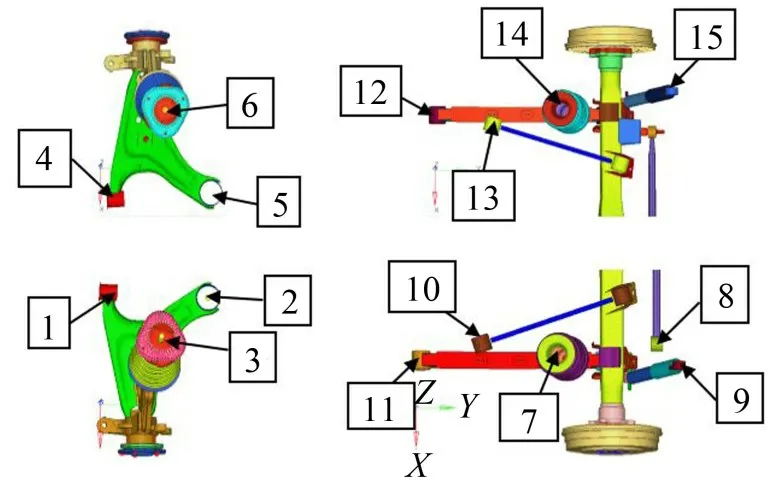
图6 车身和底盘系统耦合连接处接附点编号

2.2 采集数据

基于逆子结构传递路径方法可知，测量轮轴头（激励点）到左后车门（目标响应点）的振动传递函数，并不需要将整车拆分几个子部件系统，仅需要在整车系统耦合状态下获得系统水平的频响函数[HS]c(a)c(a)、[HS]c(b)c(b)、[HS]c(b)c(a)、[HS]o(a)c(a)、[HS]c(a)i(b)、[HS]c(a)i(b)。测试工况为车辆在搓衣板路面以13 km/h行驶，在每个耦合接附点的主被动侧两端相应位置各安装1 个3D 振动加速度传感器如图6(b)所示，耦合接附点个数为15个，因此共需要安装30个振动传感器，将测取信号作为传入车身系统的输入信号。参考汽车行业标准QC－T747－1999，选取后车门靠近C柱上部位置为目标响应点，安装一个加速度传感器测取响应信号，如图7（b）所示。整车形成“轮轴头振动激励-耦合处接附点-后车门目标响应点”的振动系统，振动能量传递路径可分为底盘系统的4×45条轮轴头处激励力到接附点传递路径输入，车身系统的45×1 条接附点到车门处响应点的输出传递路径，文中只考虑垂直路面激励。

图7 加速度传感器安装位置

把通过试验测取的系统频响函数数据代入式（3）～式（6）中，求解出非耦合状态下子结构传递函数和耦合界面连接元件动刚度。为了验证用本文所提出方法的可靠性，将根据式（7）计算出左前减震器接附点Z向（垂直路面方向）激励到左后门X向（车宽方向）响应点之间的传递函数，与通过对应试验测量所得传递函数曲线对比。如图8表示，两曲线在0～400 Hz 频率段内曲线走势基本相同，幅值差异为11%，在可接受误差范围内。

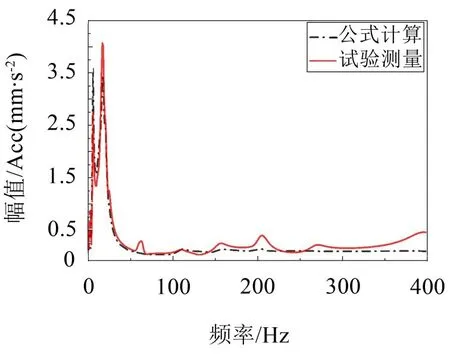
图8 根据公式计算所得的频响函数曲线与试验结果对标

2.3 试验结果分析

通过式（3）～式（6）计算求解出的激励传递率、整车连接耦合综合动刚度C、响应灵敏度，其值大小如图11至图13柱状图所示。结合左后门异常振动的振动水平，找出路径贡献量大的主导路径，进一步对贡献量较大的路径中激励传递率和响应灵敏度分别进行对比和分析，为后期的优化设计提供一个方向更明确的方案。根据实际工程要求，取1 000 N/mm 和10 000 N/mm 为上下极限参考刚度曲线，前期已经得到各接附点在0～400 Hz内动刚度曲线，通过与参考刚度曲线对比分析，看出各接附点动刚度幅值都在参考刚度曲线所在区域内，满足抵抗来自路面振动激励所引起动态形变的条件，因此不考虑工况载荷对目标响应点影响。

2.3.1 激励传递率分析

激励传递率的定义为：被动端耦合处接附点自由度j向（车身侧c(a)）所受力除以轮轴头自由度i向所施加激励力[11]。

FCj,k、Fi,k、TCj,k分别表示车身侧接附点所受力、轮轴头受路面垂直方向激励力、激励力传递率。激励力传递率提供一种直接评价标准量，也是振动路径贡献量关键组成部分。它可以评估从轮轴头激励-车身侧接附点的传递路径中振动能量过滤情况，参考文献[11]，激励力传递率另一种表达式为：

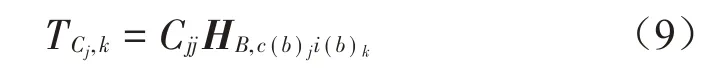
式中：Cjj、HB,c(b)ji(b)k分别表示耦合处接附点自由度j向连接动刚度、非耦合状态下子结构B(底盘系统)第k个轮轴头振动激励到耦合处接附点（底盘侧）自由度j向的传递函数，即激励灵敏度。

从图9 中可以看出左前轮轴头Z向分别到左前减震器接附点X、Y、Z向的激励力传递率曲线，Z向（车高方向）幅值在大多数频率段内高于自由度X、Y的幅值。车辆行驶过程中4个轮胎同时接受来自路面激励，因此某一个耦合处接附点输出量是4 个轮胎共同激励的结果。考虑为实际汽车行驶过程中振动能量传递情况，以及为进一步高效率找出最大路径贡献量的关键因素，参考文献[12]中公式：

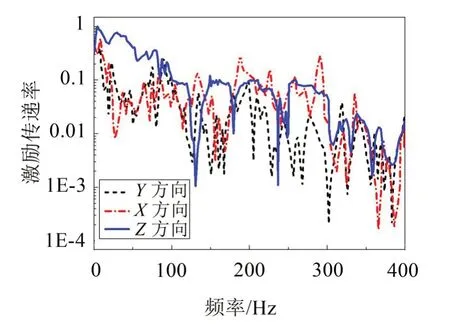
图9 左前轮轴头到左前减震器的激励力传递率

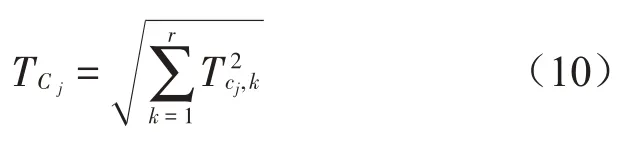
式中：r表示轮轴头激励点个数（本文中r=4），TC j表示所有激励点（轮轴头）到响应点自由度j向的激励传递率的均方根总和。

从图10看出自由度Z向幅值曲线在大多数频率段内高于X、Y两个自由度，这也间接验证了式（10）计算方法的可靠性。其他14个耦合接附点（车身被动侧）激励传递率可以通过式（10）计算求出，图11中以柱状图方式表示各接附点激励传递率大小。图11 中编号7、11、12、15 柱状图高度明显高于其他接附点对应的柱状图，这表示轮轴头自由度为Z向的激励产生的振动能量在传递到各接附点（车身侧）的过程中衰减各不相同，其中接附点7、11、12、15对振动能量的衰减效果相对较差。因此下一步对组成激励传递率的两个部分即系统耦合动刚度C和激励灵敏度进行进一步分析。由于底盘系统相对复杂，研发周期很长，优化底盘部件参数可行性很小，因此下文对耦合系统综合动刚度C进行计算分析。

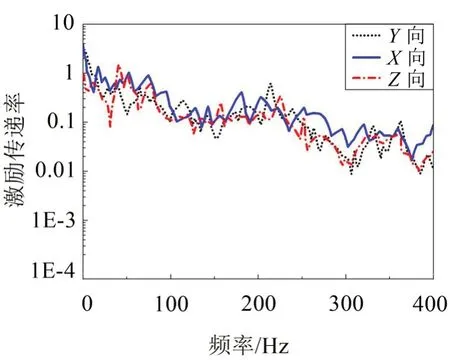
图10 左前减震器接附点激励传递率均方根总和曲线

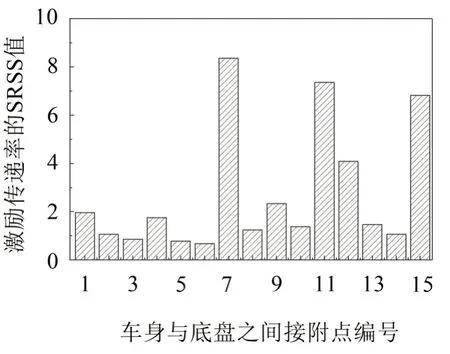
图11 各接附点激励传递率的均方根总和柱状图

2.3.2 系统综合动刚度C和响应灵敏度分析

上文已证明接附点动刚度满足抵抗动态下结构形变要求，所以本文只针对振动能量传递函数进行分析。根据式（1）可知，系统传递函数是由非耦合响应频响函数HA,o(a)c(a)j、耦合系统综合动刚度C、激励灵敏度HB,c(b)j i(b)构成，上文中已对每个耦合接附点激励传递率进行计算。下一步分析响应灵敏度和综合动刚度C，本次研究的整车系统的底盘和车身之间耦合接附点共15 个，每个接附点有3 个平动自由度，所以接附点到车门响应点共有45条HA,o(a)c(a)j响应传递函数（响应灵敏度）。由于每个自由度之间可视为相互独立，而且各自由度之间结构振动传递函数的振动形态和频率相差较大，因此每个振型的振动是相互独立的，本文借助SRSS 方法（振型组合法或平方和开平方根法）计算响应传递函数和系统综合动刚度C[13]。

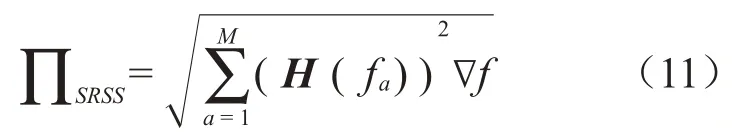
其中：∏SRSS表示所关注传递函数曲线在Δ（f0～400 Hz）范围内能量的大小，M为指定频率范围内传递函数曲线个数。因为各接附点自由度之间相互独立，每个耦合接附点都起到传递3个平动自由度方向（X向、Y向、Z向）振动的作用，因此把每个接附点当做一个综合体结构进行计算分析将会更加简洁直观。通过式（1）求解出耦合综合动刚度C、子结构A传递函数(HA,o(a)c(a)j)的SRSS 值，其计算结果以柱状图形式显示依次如图12至图13所示。

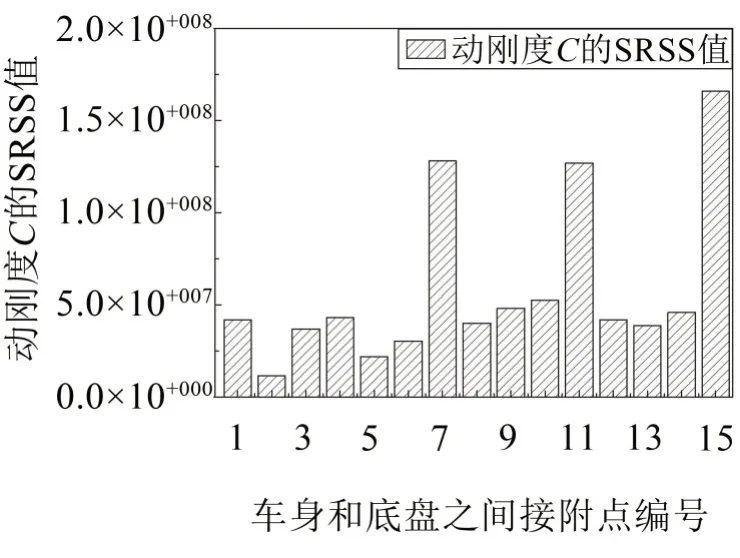
图12 整车振动系统耦合动刚度C的SRSS值

图13 接附点到响应点的响应灵敏度SRSS值

从图12 所示柱状图可以看出，编号7、11、15 耦合综合动刚度的SRSS值明显大于其他接附点的值，且这与图10 中接附点幅值较大编号7、11、15 相对应。这证明了综合动刚度C是导致接附点7、11、15的激励传递率SRSS值过大原因。从图12可以看出其他柱状图高度相差不太明显。经综合分析可知，接附点7、11、15综合动刚度过大对左后门异常振动的贡献最大。

3 结语

本文研究一种基于多点刚柔耦合逆子结构的传递路径分析方法，并将此方法应用于研究某款SUV以速度11 km/h～13 km/h低速行驶在搓衣板路面上时出现的后车门异常振动问题，基于该方法实现了在整车振源耦合状态下，利用试验所测取的系统级水平传递函数求解出非耦合子结构传递函数及连接件动态特性，对贡献量较大的传递路径进行逐步分解、分析，最终找出对主要传递路径影响较大参数：接附点7、11、15的综合动刚度参数C，为进一步优化设计提供一个更明确方向。