减水剂下废石全尾砂充填料浆管输阻力计算模型

尹升华， 郝硕， 张海胜， 胡胜， 曹定洋

(1.北京科技大学 土木与资源工程学院， 北京 100083； 2.金属矿山高效开采与安全教育部重点实验室(北京科技大学)， 北京 100083； 3.中国恩菲工程技术有限公司， 北京 100038)

受选厂排废量与尾矿库基建成本的制约，废石尾砂胶结充填工艺逐渐应用于金属矿山[1-2]。地下金属矿山充填开采通常需要架设数百米甚至数千米的输送管道，用于连接充填料浆制备室和采场充填作业面，该过程中料浆的管输效率是决定充填成本与充填质量的关键因素[3-4]。由于减水剂具有提升料浆流化润滑性的作用[5]，能够在单位用水量恒定的条件下改善高浓度充填料浆的和易性[6-7]。近年来矿山充填领域对减水剂的应用研究不断深入，取得了大量的研究成果。

王洪江等[8]研究了添加减水剂后全尾砂膏体屈服应力随时间的变化规律，结果表明膏体质量分数为80%、减水剂掺量为0.03%时，全尾砂膏体屈服应力随时间的增长呈先降低后上升的趋势。饶运章等[9]针对超细全尾砂膏体料浆，研究了多水平下的聚羧酸减水剂对坍落度和泌水率的影响规律，回归发现料浆质量分数为70%～76%、聚羧酸减水剂的质量浓度为0.50%时，膏体充填料浆和易性改善效果良好。Chandra S等[10]通过对新制备的料浆开展流动性参数测定试验，提出了萘系减水剂对电位的影响能力大于聚羧酸减水剂的影响能力，但二者相比聚羧酸减水剂提高浆体流动性效果更显著。范作鹏等[11]分析了萘系高效减水剂、聚羧酸高效减水剂、氨基高效减水剂以及脂肪族高效减水剂的作用效果，认为4种减水剂能有效提高全尾砂充填料浆的流动性，但凝结时间有所拉长。陈庆等[12]开展了向水泥基浆体中添加高效减水剂试验，基于中心粒子模型推演结果构建了超高性能水泥基材料的水化动力学模型。薛振林等[13]通过研究泵送剂对充填料浆流变参数和充填体强度的影响，优化了泵送剂的掺量，给出了最低成本条件下的最优配合比。李翠平等[14]讨论了不同剪切速率与加载时间下的多浓度全尾砂膏体屈服应力变化情况，认为峰值屈服应力、静态屈服应力正比于膏体的测量速率，动态屈服应力反比于测量时间；通过分析颗粒网络结构等细观尺度的参数，解释了全尾砂膏体屈服应力易变性。尹升华等[15]开展了尾砂膏体料浆的流变试验和塌落度室内试验，以充填料浆质量浓度为自变量，构建了全尾砂膏体管输阻力计算模型，结果表明采用料浆质量浓度或塌落度的管输阻力计算模型可靠。王少勇等[16]基于新型闭路的环管实验，揭示了骨料粒级组成、充填管径、浆体流速和料浆质量浓度对全尾砂膏体料浆管道输送压力损失影响规律，结果表明，压力损失随流速增大而增大，随管径增大而减小，随质量浓度增大而增大。张兵等[17]研究了基于流体力学理论分析了倾斜管道中料浆的受力情况，同时分析了膏体流变特性的4种影响因素的敏感性，认为灰砂比的影响作用不显著，细尾砂含量为12%、碎石含量为4%时的料浆流动性良好。兰文涛等[18]通过分析充填料浆的流动状态确定了层流临界条件，基于推演的近似管道流量方程计算特定管径、管长和压差的条件下的料浆输送流量，结果反演发现近似管道流量方程可靠。王永定等[19]针对某镍矿充填成本高、充填材料供不应求的问题，探索了废石粗骨料、废石-棒磨砂混合粗骨料高浓度料浆自流输送与强度配比实验，结果发现废石/棒磨砂的值处于5∶5～6∶4区间内既满足强度要求，也满足长距离输送要求。

废石的细粒度颗粒少且破碎难度大成本高，其与细粒度的全尾砂混合充填使用可实现高效的资源化利用等[20]，但关于废石全尾砂混合料浆的管输摩阻方面研究较少。但对于仅用废石与全尾砂混合制备的胶结料浆的流变特性研究较少，对于适配于该种料浆的减水剂用量及作用机理的研究更显匮乏，为此，本文针对掺有PC-P的废石尾砂充填料浆，分析了不同减水剂掺量条件下的料浆流变特性，构建了屈服应力、塑性粘度与废尾比、料浆质量浓度、胶砂比和减水剂掺量的多种回归模型，通过误差分析优化了料浆流变参数。基于料浆管输过程中的手里分析与数学表达式推导，求解了不同条件下的管输摩阻计算新模型，经验证模型可靠，为充填输送工艺提供一种思路。

1 实验材料与流变实验

1.1 实验材料

实验中所用的全尾砂取自国内某镍矿浓密后的泵池，废石取自废石场。废石、全尾砂的物理化学性质如表1所示。废石的主要成分为含矿超基性岩带的肉红色细粒花岗岩和含辉橄榄岩，破碎粒度范围0.20～12.00 mm，其碱活性计算结果为惰性材料，无碱集料反应(alkali-aggregate reaction，AAR)影响。全尾砂的粒级范围为0.28～447.74 μm，主要分布于10～80 μm(d10=2.22 μm，d50=16.89 μm，d90=75.99 μm，其中d10、d50和d90分别为全尾砂质量分数为10%、50%和90%时对应的粒径)。废石、全尾砂的粒径分布曲线如图1所示。实验减水剂为市售的聚羧酸减水剂，减水率不低于14.00%，含气量不高于3.00%，初凝终凝时间差-90～120 s。水泥为市售水泥，型号为国标PC42.5R普通硅酸盐水泥，密度1.30 kg/m3，凝结时间范围45～600 min。

表1 物料的物理化学性质Table 1 Physical and chemical properties of materials

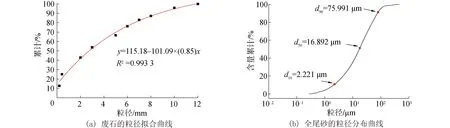
图1 物料粒级分布Fig.1 Material size distributions

1.2 实验设备与步骤

实验所用流变仪为BROOKFIELDR/Splus型流变仪，使用规格为v40-20的桨式转子, 配备自动数据采集软件Rheo3000。实验步骤为：控制实验环境温度(20±2)℃，安装桨式转子，将充分搅拌的料浆置于置物台上后，下放转子至距离样品容器底部30 mm处待测。设置测定程序，实验采用控制剪切速率法(controlled shear rate，CSR)进行测定，程序设定0～5 s转子剪切速率为5 s-1，6～120 s转子剪切速率为220 s-1。

1.3 实验原理及方案

充填料浆的流变特性就是在外力作用下研究对象的流动变形规律。废石-尾砂料浆的流变特性受多因素多条件的影响，若外力使料浆的运动状态发生变化，则该料浆此时的流变特性也会受到影响。依据料浆不同的流变特性，可将研究对象划分为牛顿体和非牛顿体。牛顿体料浆的剪切应力与剪切速率呈线型相关关系：

τ=μγ

(1)

式中：τ为剪切应力，Pa；μ为粘度系数，Pa·s；γ为剪切速率，s-1。

非牛顿体依据料浆的性质划分可归属的模型有幂律流体、赫切尔—巴尔克模型(H-B)和Buckingham流体模型。计算管道输送的阻力，需首先从料浆流变模型、流变参数和流变特性曲线等角度入手，通过调整优化关键参数的阈值，从而做出符合特定输送情况的料浆配合比决策。因此，经前期大量预试验总结，兼顾矿山经济高效、绿色环保的生产理念，在灰砂比为1∶4的条件下，设计不添加PC-P减水剂的废石尾砂充填料浆流变实验，废尾比分别为5∶5、6∶4和7∶3的条件下，测定料浆质量浓度为73%、75%和77%时的剪切应力。

2 废石尾砂充填料浆流变特性

水浴温度为21 ℃，未添加PC-P的废石尾砂的充填砂浆流变曲线如图2所示。图中流变曲线的分布形态为一条与剪切应力轴相交的直线，剪切应力与剪切速率呈现正相关关系。当剪切应力超过剪切应力轴端截距时，料浆具有流动趋势，表现出屈服流体的特征，符合Buckingham流体模型：

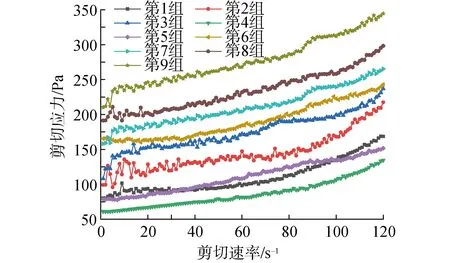
图2 未添加PC-P的废石尾砂充填料浆流变曲线Fig.2 Rheological curves of waste rock taillings filling slurry without adding PC-P

τ=τb+μbv

(2)

式中：τ为剪切应力，Pa；τb为屈服应力，Pa；μb为Buckingham粘度系数，Pa·s；v为剪切速率，s-1。

该类料浆为内部粒子间结合力强的多相混合体系，当粒子浓度达到能够让粒子间相互接触摩擦时，形成粒子的三维网格结构，屈服应力值可以直接描述这一结构的强弱程度。基于该模型，对剪切速率与剪切应力线性回归，获得流变特性参数方程，如表2所示。

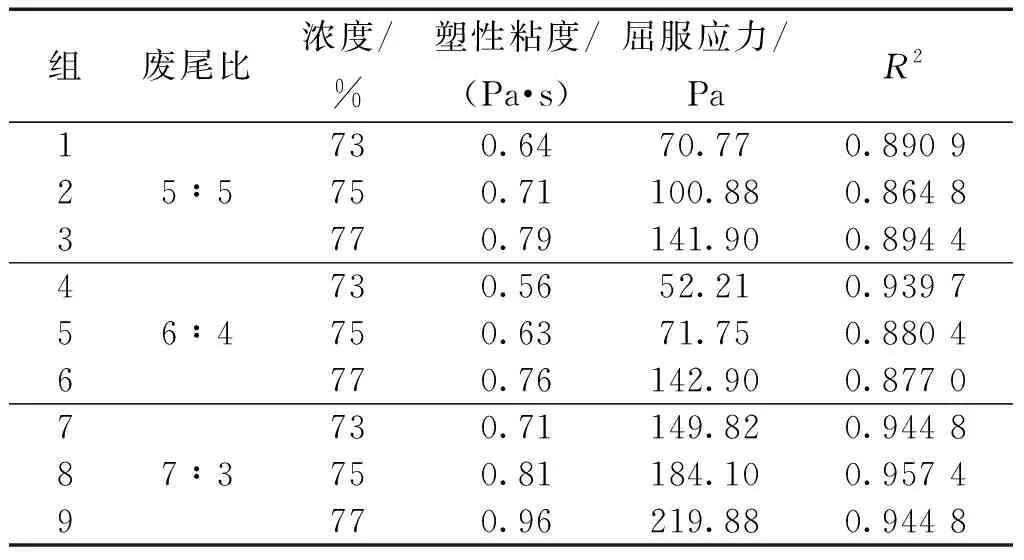
表2 流变特性与线型回归结果Table 2 Rheological properties and linear regression results

依照表2的线性回归结果，相同质量浓度条件下，屈服应力随废尾比的增大呈现先减小后增大的趋势。在相同废尾比条件下，料浆屈服应力与质量浓度呈正相关关系，由低到高的3种废尾比情况下，屈服应力的相对差量分别100.52%、173.68%和45.18%，该现象可能与堆积密实度有关。依据二维度堆积密实度理论：

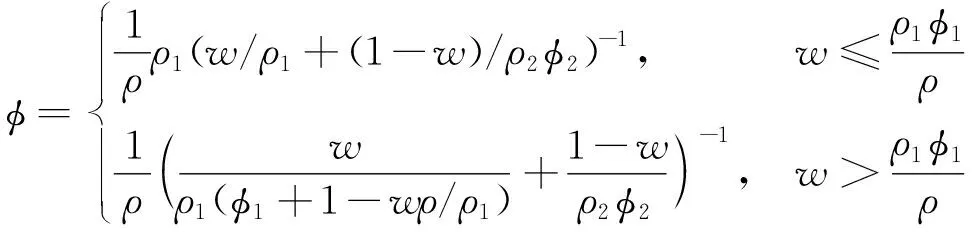
(3)

式中：ρ1为废石粗骨料容重，t/m3；ρ2为全尾砂细骨料容重，t/m3；ρ为2种骨料的混合容重，t/m3；ρ=[ω/ρ1+(1-ω)/ρ2]-1,0≤ω≤1；φ1为废石堆积密实度；φ2为全尾砂堆积密实度；ω为废石占骨料的质量分数，%。

计算得出废石尾砂的混合堆积密实度，如图3所示，废尾比的值为1.50时料浆的堆积密实度最大。

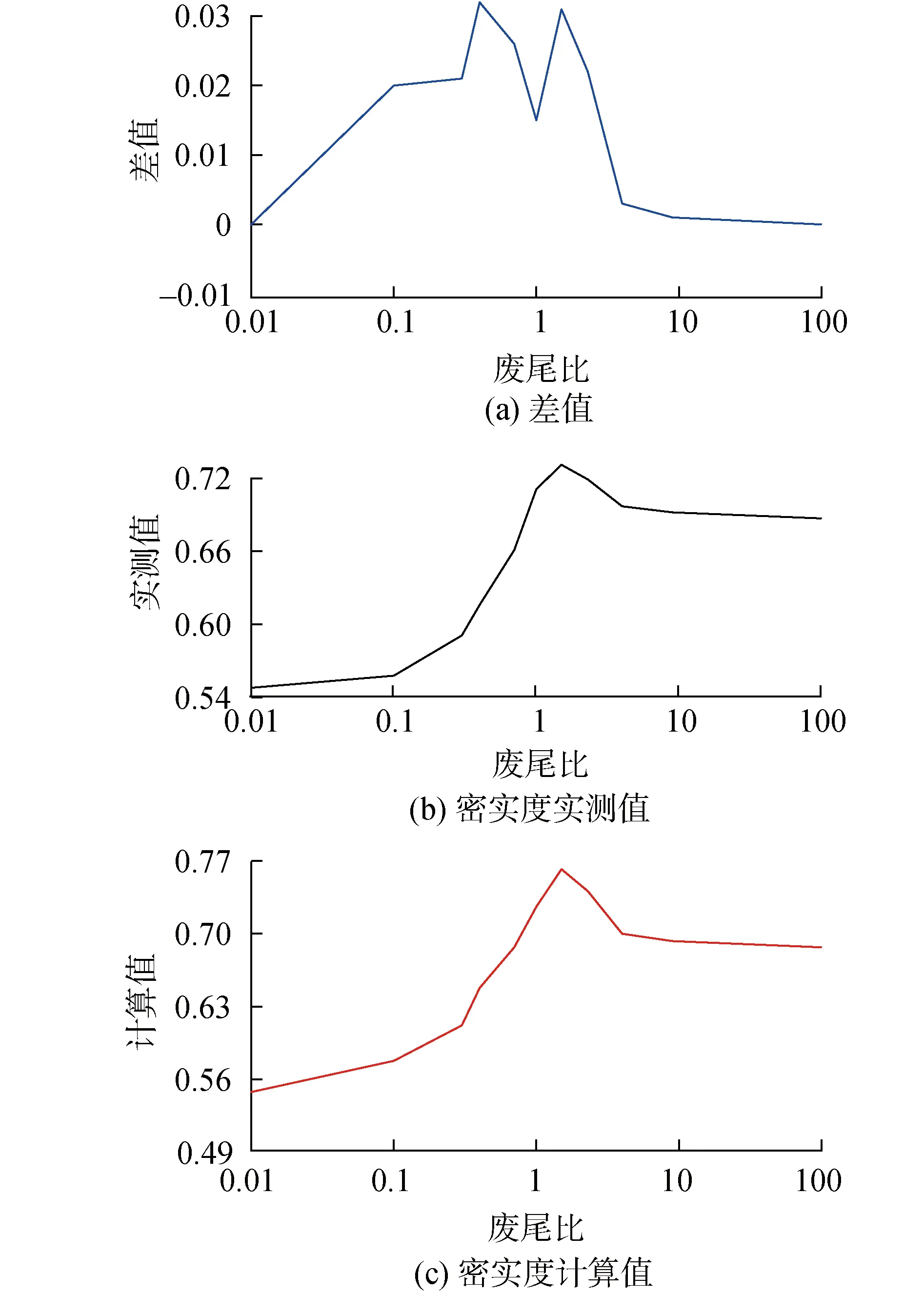
图3 堆积密实度的计算值与实测值Fig.3 Calculated and measured values of packing density

由图可知，当废尾比小于1.50时，混合骨料的堆积密实度随废尾比增加而增大，因为该阶段废石之间的孔隙量增加，尾砂恰好填充于废石的裂隙中，骨料之间的嵌锁水平不断提升，该过程的流变过程也从“无序”逐步趋于“有序”，即料浆复杂体系的熵增过程，熵值越大堆积密实度越大。当废尾比等于1.50时，此时废石的质量分数ω=60%，混合骨料的堆积密实度最大，骨料之间的嵌锁水平到达顶峰，废石间的缝隙与尾砂的填充量完全相等，该阶段质量浓度对料浆流变参数的作用尤为显著。当废尾比大于1.50时，混合骨料的堆积密实度随废尾比增加而减小，该阶段尾砂量已经不足以填充废石之间的孔隙，废石间的“边壁效应”成为控制该阶段混合骨料堆积密实度的主要因素，故堆积密实度逐渐下降，直至趋于废石骨料的堆积密实度，该过程由“有序”再次趋于“无序”，即料浆复杂体系的熵减过程，熵值越小堆积密实度越小，料浆的质量浓度对屈服应力的影响作用降低。

3 PC-P作用下料浆的流变特性

基于上述分析，设定胶砂比1∶4，尾废比7∶3，料浆质量浓度77%的恒定条件下，设计PC-P掺量(质量分数，%)为因素变量的流变实验。前期对比不同掺量的PC-P聚羧酸减水剂、FDN萘系减水剂和AK脂肪族减水剂条件下，尾砂水泥充填料浆流变特性，分析发现PC-P质量浓度处于0～0.5%时作用效果显著。为了达到绿色矿山“降本增效”的要求，设计减水剂PC-P含量(ωPC-P，%)的水平为0.00%、0.10%、0.20%、0.30%、0.40%和0.50%共6个水平，PC-P作用下料浆的流变特性曲线如图4所示。

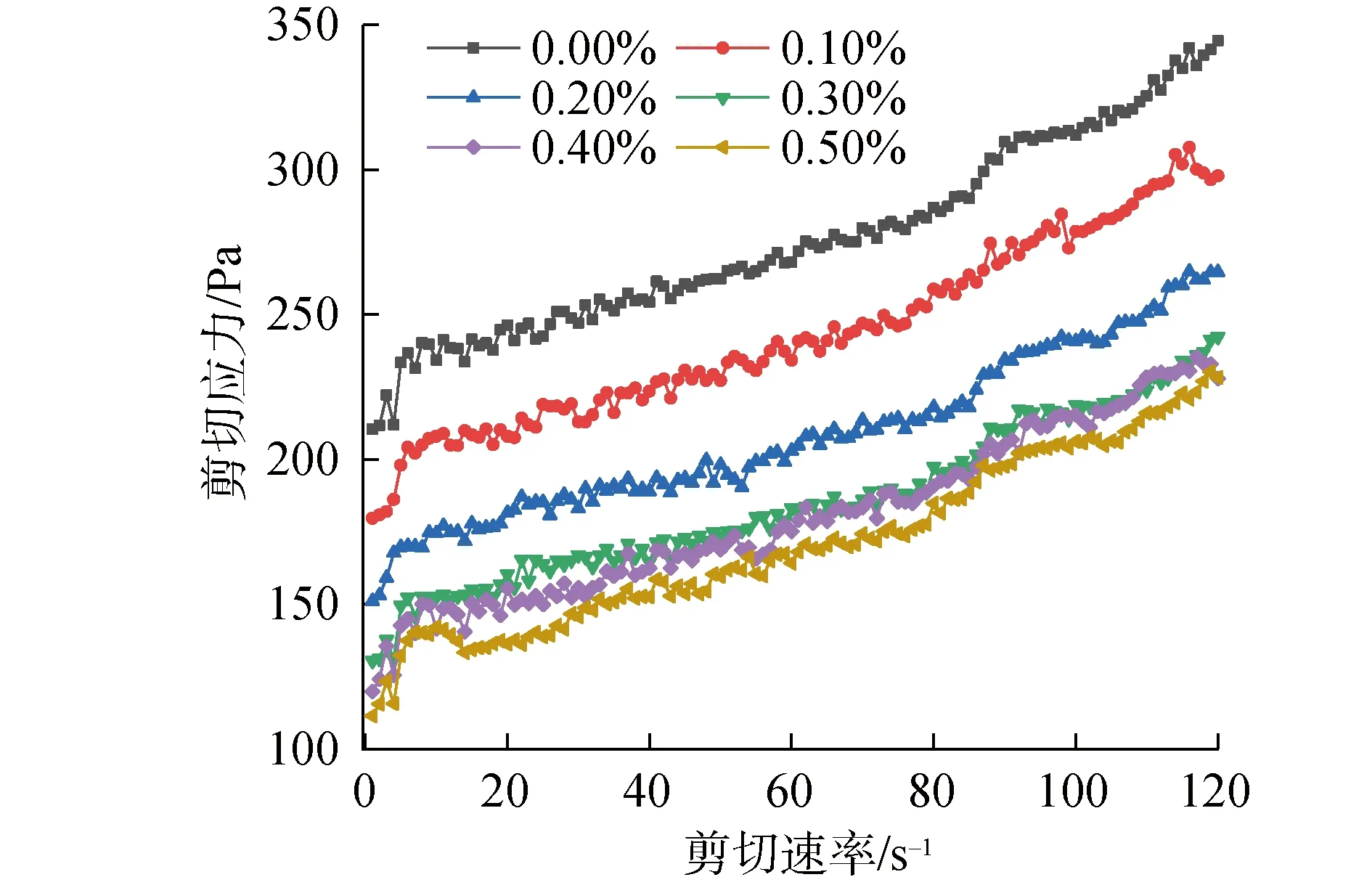
图4 PC-P作用下料浆的流变特性曲线Fig.4 Rheological characteristic curves of slurry under the action of PC-P

由图4，PC-P作用下料浆的流变特性曲线与未添加减水剂的料浆流变曲线分布情况类似，剪切应力与剪切速率呈正相关关系。随着ωPC-P的增加，相同剪切速率下料浆的剪切应力呈逐级递减的态势，说明ωPC-P的值处于[0.00%,0.50%]内时，PC-P改善了料浆的和易性，但从整体来看，PC-P对料浆剪切应力的影响程度随ωPC-P的增加逐渐减小。考虑到实验尾砂属于超细粒级，料浆体系内粒度越小的颗粒表面能越大，尾砂颗粒可能因为彼此聚团对自由水的状态和形态起到限制作用，且废石的粒径较大且不均匀度高，曲线有明显的震荡特征。故采用线性回归、多项式回归、指数回归和逻辑回归4种方法对PC-P作用下料浆的流变参数进行了回归计算[21]，不同ωPC-P的料浆流变参数如表3所示，屈服应力、塑性粘度与PC-P掺量的回归结果分别如表4、表5所示(R2为复相关系数)。

表3 不同PC-P掺量的料浆流变参数Table 3 Rheological parameters of slurry with PC-P

表4 屈服应力τ与PC-P掺量x的回归结果Table 4 Regression results of τ and x

表5 塑性粘度μ与PC-P掺量x的回归结果Table 5 Regression results of μ and x

屈服应力与减水剂掺量的回归结果中，根据显著性要求，线型回归、多项式回归、指数回归和逻辑回归的复相关系数均接近1，但塑性粘度与减水剂掺量的回归结果中，4种回归的复相关系数均未及0.90，故分别选取剪切应力、塑性粘度与ωPC-P的4组回归模型中较显著的3组，计算回归计算结果与标准结果的误差，绘制如图5的误差分析图。

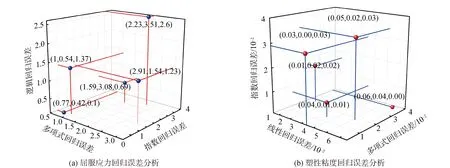
图5 回归模型误差分析Fig.5 Error analysis of regression model

依据图5(a)计算，4种屈服应力与减水剂掺量的回归模型中，多项式回归模型、指数回归模型和逻辑回归模型的累计误差值分别为8.50、9.09和5.98，对应误差所占百分比分别为1.15%、1.23%和0.81%。在显著性分析的基础上考虑误差分析，适配性最优的参数模型为逻辑回归模型，如图6(a)所示。参数方程为：

y=95.86+124.00/(1+(x/0.21)1.52)，

R2=0.998 9

(4)

依据图5(b)计算，塑性粘度与减水剂掺量的线型回归模型、多项式回归模型和指数回归模型的累计误差值分别为0.19、0.10和0.11，对应误差所占百分比分别为4.60%、2.37%和2.67%。对于塑性粘度与ωPC-P间关系的最优适配模型图6(b)所示，多项式回归模型为：

y=-0.97x+1.51x2+0.94，R2=0.866 7

(5)

综合分析，对于数学模型(4)，其给出屈服应力随ωPC-P增大持续降低，而对于数学模型(5)，当ωPC-P=0.32%时，模型取最小值0.78 Pa·s。因此，针对料浆浓度为77%的废石尾砂充填料浆，添加PC-P的最优方案为ωPC-P=0.32%时，充填料浆的屈服应力为139.57 Pa，塑性粘度为0.78 Pa·s，能够收益最大的和易性改善效果。

由图6(a)可知，废石尾砂充填料浆的屈服应力随PC-P掺量增加而降低，其逻辑回归曲线呈“先陡降再缓降”的趋势。该过程中，PC-P减水剂依靠静电斥力将料浆中被细微颗粒包围的充填水释放出来，从而降低料浆的屈服应力。同时，尾砂属于惰性材料，化学反应活性极低，其与水混合后附着于颗粒表面的电荷数量有限，为PC-P提供了一定的吸附点位，该阶段PC-P对料浆屈服应力的影响显著。继续向料浆中添加减水剂，随着PC-P分子的浓度增加，多余的减水剂分子只能处于全尾砂浆体的自由水中，PC-P对料浆屈服应力的影响减弱。同时，由图6(b)可知，废石尾砂充填料浆的塑性粘度随PC-P掺量增加呈现先下降后上升的趋势。实验设计添加减水剂的样本为质量浓度77%、灰砂比1∶4、废尾比7∶3的废石尾砂充填料浆，屈服应力达到219.88 Pa，说明固体颗粒紧密堆叠程度高。该体系中的自有水大部分用于浸润细颗粒表面，剩余的少量自由水受到PC-P大分子之间产生物理堆叠作用，逐步趋于饱和，继续向体系内添加减水剂，造成塑性粘度的反向增长。PC-P减水剂对料浆复杂体系内细颗粒作用示意图如图7所示。

图6 屈服应力和塑性粘度的最优表征Fig.6 Optimal characterization of yield stress and plastic viscosity

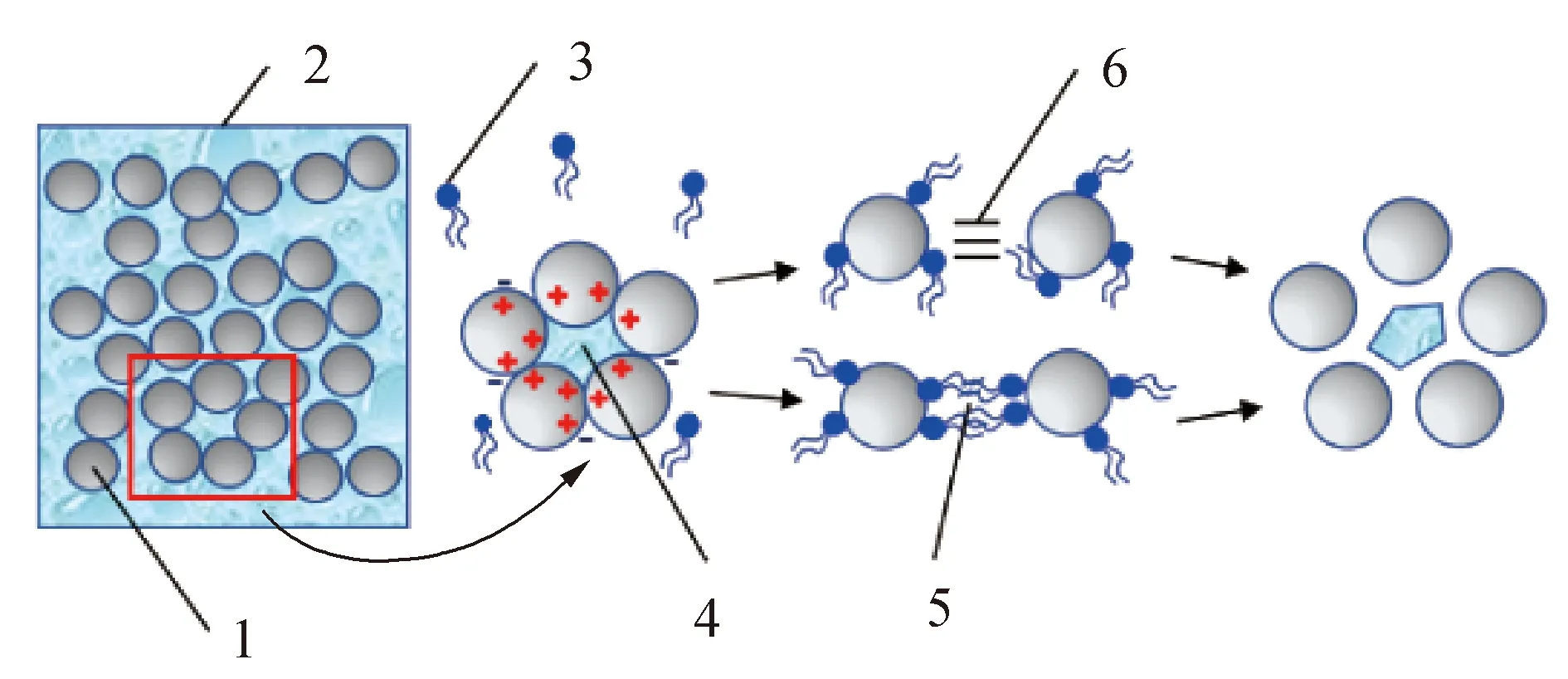
注：1.细颗粒，2.料浆体系，3.PC-P减水剂，4.结合水，5.空间位阻力，6.静电斥力图7 PC-P在废石尾砂料浆中的作用机理示意Fig.7 Schematic diagram of the action mechanism of PC-P in waste rock-unclassified pastes slurry

4 料浆管道输送摩擦阻力计算模型

使用减水剂的充填料浆固相含量一般较大，在高浓度废石尾砂充填料浆复杂体系中，牛顿流体和固液两相流模型均无法准确描述料浆流动性，在矿山及相关领域的应用与研究中，常把高浓度料浆看作塑性粘度大的非牛顿流体。为了表征添加PC-P后料浆的流动性，在添加PC-P的研究基础上，构建料浆管道输送的阻力计算模型。充填料浆在水平圆形管道输送过程中的受力分析如图8所示。

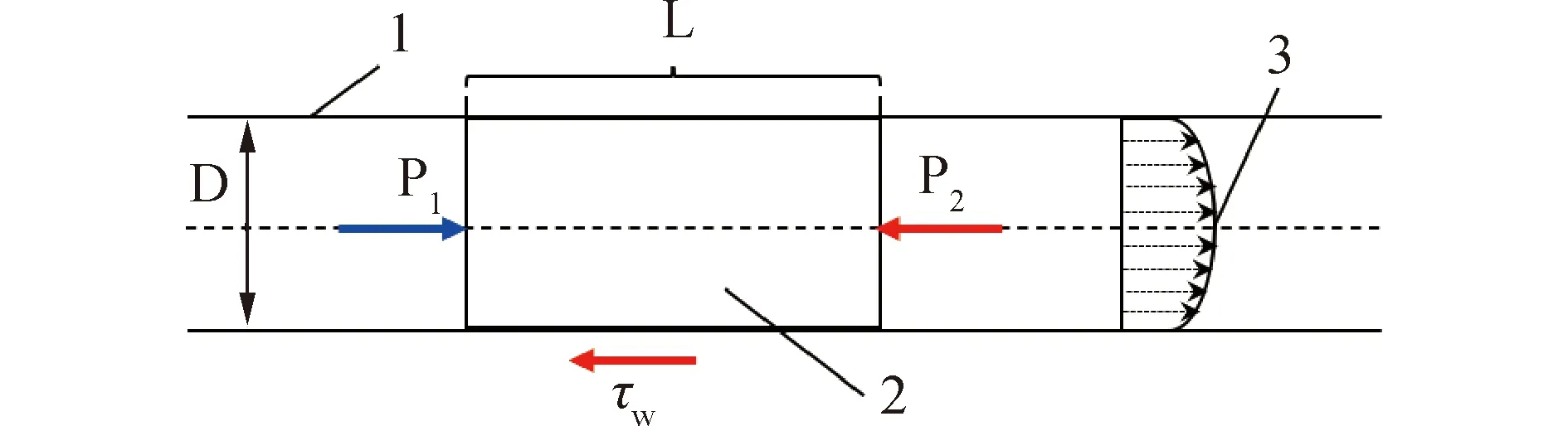
注：1.充填管道管壁，2.分析受力的料浆微元，3.流动方向图8 充填料浆管道输送受力分析Fig.8 Force analysis of conveying micro-element

在管道中取长度为L的一段微元体进行受力分析：

(6)

式中：τw为料浆在管壁处的切应力，Pa；D为管道内径，m；L为微元体长度，m；P1为左端面的压强，Pa；P2为右端面压强，Pa；ΔP为管长L的压力损失，即ΔP=P1-P2，Pa；im为摩阻损失，Pa/m。求解方程可得：

(7)

对于废石尾砂充填料浆的实验样本，其特性与Buckingham塑性体基本吻合。基于Buckingham理论模型推演料浆层流区管壁切应力τw与流速v关系为：

(8)

式中：μ为料浆粘度，Pa·s。在乘积关系中，底数小于1的高次幂项经多次迭代后值趋于0，为划定误差范围，选取误差分析中的最大误差4.60%为阈值，计算添加PC-P条件下屈服应力与最大剪切应力的比值结果如表6所示，其中τ0为料浆的屈服应力，Pa；τwmax为料浆的最大剪切应力，Pa。由表可知，当PC-P含量(ωPC-P，%)为0.20%～0.50%时，满足设定阈值，即当τ0/τw<0.6时，τ0/τw的4次项的值分别为4.00%、4.00%、3.00%和2.00%均小于4.60%，认为该项可以忽略，结合推导式(7)，基于Buckingham理论模型推演的料浆管输阻力为：

(9)

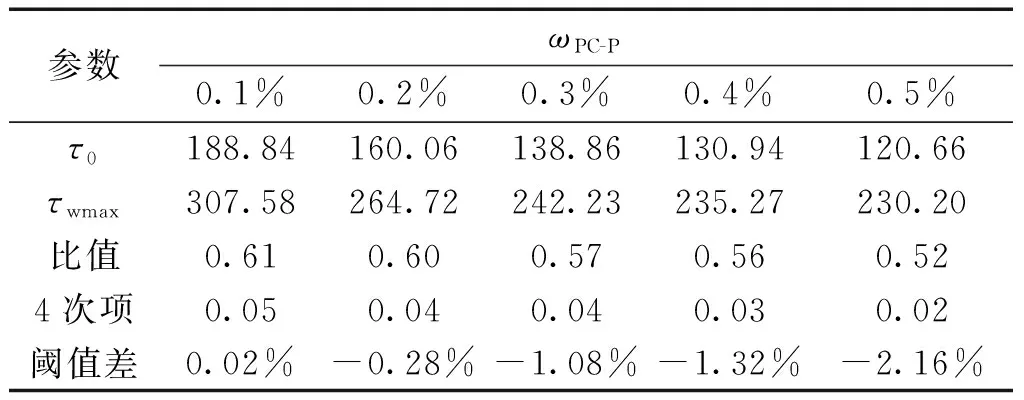
表6 屈服应力与最大剪切应力及其比值Table 6 Yield stress and maximum shear stress and ratio

当ωPC-P=0.10%时，该模型可推演为一元五次方程，求解该模型需借助高次幂的DOA跟踪算法[22]，化简结果为：

(10)

综上所述，添加PC-P减水剂的废石尾砂胶结充填料浆的管道输送阻力模型为：

(11)

对于倾斜管道，料浆除了克服沿程的管道阻力以外，还应加上一个固体重量垂直分量，故倾斜管道的管输阻力可以表征为：

i′=im+Cv(ρs-ρw)sinθ

(12)

式中：i1为倾斜管道沿程泵压，Pa/m；im为水平管道的沿程阻力损失，Pa/m；Cv为浆体的体积浓度；ρs为固体颗粒密度，kg/m3；ρw为清水密度，kg/m3；θ为倾斜管道倾角，(°)。

本试验的样本料浆管道阻力计算基于国内某镍矿的工程材料，依据该矿山某段水平管道验证计算模型的准确性，其规格为内径152 mm，充填料浆流速设定为2.4 m/s，对照该矿山原有的经验公式与计算模型的管输阻力损失，绘制模型对比差值图。计算结果如表7所示，数据曲线如图9所示。

表7 PC-P作用下2种管输阻力模型对比Table 7 Pipeline resistance model pair by PC-P

图9 PC-P作用下计算模型与经验模型对比Fig.9 Comparison of two models of PC-P slurry

通过验证结果可知，当ωPC-P为0.20%时，计算模型与经验模型的管道输送阻力差值达到最大172 Pa/m;当ωPC-P为0.30%时，计算模型与经验模型的管道输送阻力差值为最小44 Pa/m，输送阻力的计算值相差不足1 kPa。综上，不同的PC-P浓度下，管道输送阻力的计算模型与经验模型结果相似程度高，PC-P作用下的废石全尾砂管输阻力计算模型准确，为矿山添加减水剂的高浓度废尾充填输送工艺提供一种思路。

5 结论

1)充填料浆ωPC-P=0时，质量浓度分别为73%、75%和77%的充填料浆屈服应力均随废尾比的增加呈先减小后增大趋势；而在相同的废尾比条件下(5∶5、6∶4或7∶3)，料浆屈服应力与质量浓度呈正相关关系，且废尾比为1.50时料浆骨料的堆积密实度最大。

2)构建了4种不同的回归模型，分析了不同的PC-P掺量对料浆屈服应力和塑性粘度的影响效果，经模型的显著性筛选与误差分析，结果表明屈服应力与ωPC-P关系的最优表征为逻辑回归模型，塑性粘度与ωPC-P关系的最优表征为多项式回归模型，两模型的交集最优解为ωPC-P=0.32%，此时充填料浆的屈服应力为139.57 Pa，塑性粘度为0.78 Pa·s。

3)低浓度PC-P依靠静电斥力释放出料浆中被细微颗粒包围的充填水，显著降低料浆的屈服应力；随ωPC-P增加，PC-P出现过饱和现象，大分子之间产生物理堆叠作用，少量的自由水无法溶解多余的PC-P分子，PC-P对料浆屈服应力的改善效果减弱，塑性粘度反向增长。

4)基于充填料浆在管道内的受力分析结果与Buckingham理论模型，推演了添加PC-P条件下的料浆管输阻力计算数学表达式，通过对参数方程高次幂项的阈值划分，以ωPC-P为划分依据分类讨论了管道输送的阻力计算模型，结果表明计算模型的输送阻力输出值与经验公式相差不足1 kPa，模型可靠，可供矿山工作人员参考。