复杂工程约束下基于NSGA-III的车身梁截面优化设计

张鸣鹤, 熊志华, 侯文彬,2

(1.大连理工大学 汽车工程学院，大连 116024；2.大连理工大学宁波研究院，宁波 315016)

1 引 言

车身薄壁梁具有较高的刚度-质量比，其力学性能由其截面形状(图1(a))决定，进而影响车身整体的力学性能。在汽车概念设计阶段，通常将梁截面的详细特征简化，如将复杂的过渡圆角简化为普通折弯角(图1(b))，通过焊接连接的两个板简化为一层，但其厚度是两个板之和。薄壁梁截面形状对于车身设计非常重要。Enger等[1]在复合载荷下通过边界摄动法进行了截面优化。Kim等[2]研究了汽车发生正碰时前纵梁的吸能量，并对比各种截面形状对吸能的影响。Nishigaki等[3]设计实现了FOA系统，该系统可简化白车身梁和接头结构并进行优化。Kim等[4]提出用拓扑优化方法确定梁截面加强板形状和位置。左文杰等[5]以车身弯曲刚度和扭转强度作为优化约束，以降低车身重量作为优化目标，以板厚度值为设计变量，对车身截面进行优化设计。Yoshimura等[6]将梁截面线离散化，将截面点坐标作为设计变量，然后通过遗传算法实现了梁截面形状和板厚的优化。

由于薄壁梁大多是冲压工艺的产物，不能生产出任意形状的截面。目前车身设计师多依赖于现有截面库来设计梁截面形状。截面优化是一个多目标优化问题，目标函数数量往往大于两个，而NSGA-II算法采用拥挤距离的方法来选择个体，往往在小于三个目标函数时有较好效果。当目标函数增加时，若继续采用拥挤距离对个体进行排序，会出现算法的收敛性和多样性不好的问题(即得到的解在非支配层上分布不均匀，这样会导致算法陷入局部最优)。如何设计合适的梁截面形状控制方法并同时兼容各种工程制造约束成为当前待解决的问题。

对于梁截面优化模型及工艺约束处理方法，王增飞[7]将焊点距离进行等分得到截面控制点坐标，解决了优化过程中产生的截面负角和板交叉等问题，但未能解决实际制造过程中冲压角和线段长度等约束。桂春阳等[8]推导了多室复杂截面的力学特性公式。对冲压工艺约束进行了数学定量描述并进行了截面优化，但其对于设计变量范围的控制方法具有局限性。本文首先提出一种梁截面形状控制方法，并基于梁截面形状控制方法给出设计变量的定义方法，推导出设计变量关于工程约束的约束公式。在满足工程约束的前提下，对梁截面进行优化设计，寻求最小截面面积，以达到车身梁轻量化设计的目的。结果表明可有效提高新车概念设计阶段的开发效率。

2 车身梁截面设计的工程约束

梁截面一般由多层板焊接而成[9]，如图1所示。层数通常为一层～四层。设计截面时首先要使截面属性满足设计人员的要求，截面属性主要包括面积(A)、惯性矩(Iy,Iz和Iy z)和扭转常量(J)等，此外还需要使截面面积尽量小，以实现减重轻量化的目的。设计截面时，可调整的变量为每层板的厚度和截面形状，因此截面设计的约束主要是组成截面板的厚度和形状。

图1 车身典型截面

2.1 形状约束

截面形状由截面控制点的坐标控制，截面形状优化问题等价于截面控制点坐标变化问题。控制点坐标变化是连续的，其变化范围受装配和制造等诸多工程因素制约。对于某些多层截面，其外板和内板的形状需要和其他部分进行装配，形状不可更改，只能调整其加强板来进行优化，如车身B柱。由于截面板由冲压工艺制造，故设计时不能产生负角(图2(a))，相邻板间不能出现负角(图2(b))，纵向和横向变形也受到一定约束(图2(c))。某些特殊截面对截面纵向和横向距离范围提出严格约束，沿板方向控制点变化产生的角度即冲压要求的拔模角应大于某一角度，同一层截面相邻两控制点之间距离即最短线段长度需大于某一值(图2(d))。为解决上述问题，现开发一个综合的截面设计工具，在满足各种约束条件下对截面的材料厚度和截面形状进行优化，满足设计人员需要的性能。

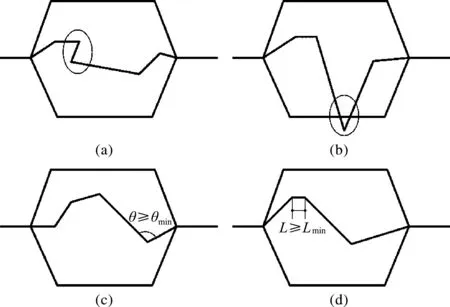
图2 截面工程约束

2.2 材料约束

当前车身材料仍大多采用价格低廉的普通钢。但镁铝合金以及碳纤维复合材料等也逐渐开始应用在汽车上，这些板的厚度一般从(0.7，0.8，1.0，1.2，1.5，1.8，2.0) mm 中选择，是一个离散类型的变量。车身设计人员必须从供应商可提供的厚度中进行选择以进行车身设计。

3 截面优化模型设计及约束处理

梁截面优化设计问题需要确定优化三要素并选择适合此问题求解的优化算法，下面进行优化模型定义。

3.1 优化目标函数

截面属性直接影响截面对应梁的弯曲扭转性能，同时也是其刚度计算和模态计算基础。截面分为开口和闭口两部分，若截面包含n条壁段，闭口部分含有nc个腔，第i壁段如图3所示，则由弗拉索夫薄壁杆件理论[10，11]可推导下列属性计算公式。

(1)

(2)

(3)

(4)

(5)

(6)

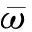
图3 截面第i壁段

3.2 优化设计变量定义

优化设计变量包括连续类型的截面形状和离散类型的板厚，截面形状是此优化问题的主要内容。梁截面形状优化受到装配和制造约束。设计变量的定义要兼容各类约束问题处理且方便优化算法应用。

如图4所示，以截面两个焊点连线为y轴，过左侧焊点做y轴垂线设为z轴，建立局部坐标系。定义设计变量Li j和θi j，其中Li j表示第i层板第j个可变化壁段的长度，θi j表示第i层板第j个可变化壁段与z轴正向之间的夹角。这样每个控制点坐标就表示成设计变量Li j和θi j的组合，即

(7)

图4 设计变量定义

3.3 工程约束处理

为保证截面控制点变化过程中满足各种约束，设计变量L和θ在算法迭代中需要受到限制。图5 为某截面实际制造约束。可以看出，主要的约束类型为长度约束、拔模角约束和装配约束，其中装配约束又包括负角和交叉约束。下面分析设计变量约束的转换。

图5 某截面制造约束

首先是最短线段约束L≥Lmin>0。为避免截面出现负角，θ的取值范围在0°～180°之间(图6(a))，大部分截面冲压工艺要求冲压角在93°～180°之间。若最小冲压角是93°，同一层截面上前一壁段的θi ,j控制着后一壁段的θi ,j + 1的变化范围(图6(b))。如果0≤θi ,j≤90°，则θi ,j +1的范围是(0°,87°+θi ,j)；如果90≤θi ,j≤180°，则θi ,j + 1的范围是(θi ,j-87°，180°)。对于板交叉约束，首先需保证每层可变化的第一壁段不产生交叉，需定义下一层壁段的角度要大于上一层(图6(c))，可通过计算板交叉点数量来判断板是否产生交叉，交叉点数Ni s p为0时，截面不发生交叉。判断两线段相交的方法，

(8)

其计算方法为[8]

(9)

(10)

(11)

(12)

(13)

(14)

图6 约束的设计变量定义

图7 线段的相交与分离

3.4 优化模型及算法实现

高维多目标优化即为目标函数数量大于3的优化问题，解之间的优劣难以判断，在进化算法领域得到广泛研究。与NSGA-II[12]不同，NSGA-III没有采用NSGA-II的拥挤距离方法，而是采用基于参考点的个体筛选方法，NSGA-III[13]利用算法预定义的参考点集控制算法对个体的筛选，在迭代过程中维持解的多样性。

由于截面优化问题至少需要优化面积和两个坐标轴的惯性矩，故目标函数往往大于等于3个，而拥挤距离方法不再适用于此问题。综上，本文采用NSGA-III算法来优化此高度非线性优化问题。梁截面优化问题描述为

(15)

4 车身截面优化设计模块开发

综上所述，为解决薄壁梁截面优化问题，现开发一个独立的截面模块FVO -Section(图8)。系统主要功能结构如图9所示[14]，包括以下功能模块。

图8 FVO -Section软件界面

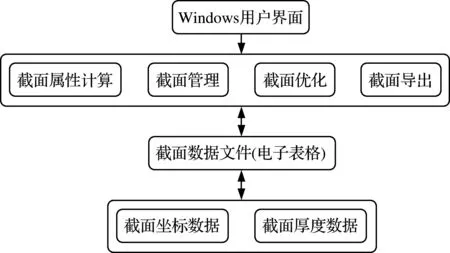
图9 截面优化系统功能结构

截面批量导入。用户需根据指定的格式编辑截面数据文件实现截面批量化导入，截面数据文件包括截面控制点坐标、板厚度和截面点连接方式。

截面属性计算。包括截面面积、惯性矩、扭转常量和翘曲常量等截面属性。用户仅需点击选中截面即可实现截面属性计算，并将计算结果显示给用户。

截面优化。包含板厚度优化和形状优化两个模块供用户选择，也可选择厚度和形状同时优化。用户可自由选择优化的板，如某些截面仅可优化加强板。用户优化前需根据需求设置截面可制造性约束。

截面导出。用户可以手动选择截面以一定数据格式导出。

4.1 优化实例

以某汽车企业提供的截面为算例，其形状约束如图10所示。提取控制点初始坐标后(图11)导入FVO -Section中计算出相应的截面属性。为方便算法优化，将点2和9设置为固定点，除角度约束e外，其余约束为此截面特有约束，需额外添加约束公式如下,

max(z8,z7,z4,z3)-min(z16,z15)=a≤74.8

y2-y9=b≤132.5

min(z6,z5)-max(z13,z12)=c≥5

min(z14,z11)-max(z19,z18)=c≥5

min(z19,z18)-max(z16,z15)=c≥5

(16)

遗传算法每一代的种群数量为100，交叉概率为0.80，变异概率为0.20。优化过程共迭代200次，多目标优化的结果是找到一系列最优解的集合，车身设计人员需根据截面属性要求从Parato解集中选取某一个解为最终截面形状。经截面属性研究得知惯性矩对梁刚度影响最大，因此拟采用以惯性矩设计值与优化结果值相差最小为标准选取解。

约束条件： a≤ 74.8 mm； b≤132.5 mm； c≥5 mm； d≥15 mm(有效搭接边，最多3层板搭接)；e≥ 98°，其他未标注所有角度均需要≥95°标注圆角的按照尺寸定义，未标注圆角尺寸的要求倒角≥2倍板厚；所有零件厚度范围为(0.7，0.8，1.0，1.2，1.5，1.8，2.0) mm。

图11 截面控制点编号

使用NSGA-III算法对算例截面进行优化。对于单一截面的优化，本文选取

取得最小值的第i个个体，在解集中以红色点标识。obj_Iy与obj_Iz为两个坐标轴惯性矩的目标值。

通过NSGA-III优化算法的优化结果、截面属性及约束值列入表1～表3。为方便设计人员进行参考，此次优化厚度值设定为连续变量，设计人员可以根据优化后的结果自行调整相应的厚度值。优化后截面的惯性矩和扭转常量都有较大提升，同时截面面积略有减小。本次优化耗时384 s，满足概念设计阶段的快速设计要求。

表1 优化结果属性对比

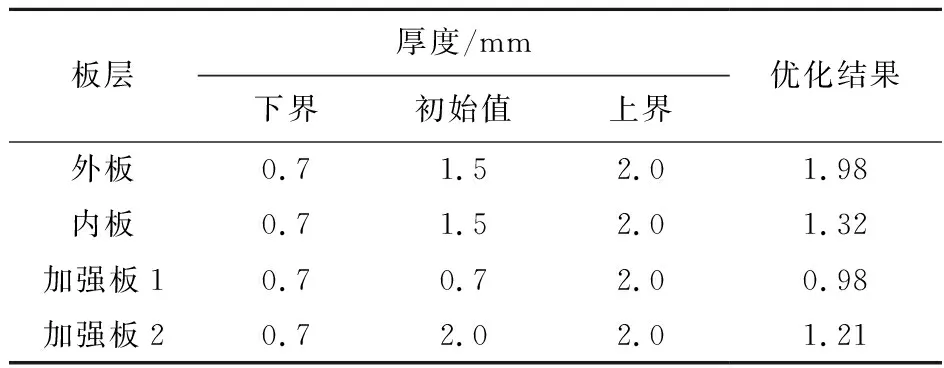
表2 厚度变量和优化结果

表3 优化前后截面性能比较

5 结 论

为处理截面优化过程中的约束问题，提出一种新的梁截面形状控制方法并推导出相应的工程约束公式，方便对冲压角和线段长度等约束进行处理。截面优化是一个高维多目标优化问题，引入NSGA-III作为该优化问题的算法，并对参考截面进行了测试。结果表明，此截面优化设计方法实现了对截面的约束，并提高了截面惯性矩和扭转刚度，同时减小了截面面积，实现了薄壁梁的轻量化设计。利用此方法可以在概念设计阶段对车身梁截面的设计提供参考，能有效提高梁截面设计效率。