基于光滑粒子流体动力学的滑油泵数值仿真

张显鹏， 徐 绯*， 吴京泽， 季 哲，杨 扬， 马春浩， 王安文

(1.西北工业大学 航空学院，西安 710072； 2.FluiDyna GmbH,Edisonstrasse 3,Unterschleissheim,D -85716 Germany； 3.西安爱生技术集团,西安 710065)

1 引 言

齿轮泵作为液压传动过程的重要元件，因自身结构简单紧凑、体积小、重量轻、工作可靠、寿命较长和维修方便[1]等优点而广泛地运用在农业机械、航空航天和工程机械等领域。依据啮合形式其结构可分为外啮合与内啮合齿轮。外啮合齿轮泵由于结构简单和成本低的优点而广泛地运用于供油泵、润滑泵和计量泵等场合[2]，但又因流量脉动、噪声相对较大和排量不可调节等缺点较难应用于高精密和超高压等环境领域；内啮合齿轮泵结构紧凑且体积小，齿轮转向相同，相对滑动速度小，磨损小，因此使用寿命长，且流量脉动和噪声都较小，使其在外啮合齿轮泵应用较为困难的领域得以广泛使用[3]。

作为齿轮泵研究的主要手段，试验广泛用于各型泵的设计当中，但针对间隙及高空低温低压等极限工况，难以大规模开展试验来提供有效数据。而伴随计算技术发展起来的数值模拟[4-6]，则为齿轮泵研究提供了一种新的思路。相比试验研究，数值模拟不仅成本较低，而且可以详细记录内部流体流动情况，提供较为完整的细节信息，便于分析研究对象的内部机理。

图1给出基于计算流体力学构建的内啮合齿轮泵流场网格模型，但由于齿轮泵内部结构以及运行原理复杂，使得在利用传统网格方法进行数值计算时，动网格技术和齿轮啮合点网格质量问题处理比较困难。并且齿轮泵内部存在的微小间隙，给齿轮泵的数值模拟增加了难度。目前常用的FLUENT和Pumplinx[7,8]均可较好地解决网格设计的诸多问题，但其划分网格的前处理和条件设置的复杂性以及计算时间较长，都在一定程度上延长了齿轮泵的研究周期。

图1 流场网格模型

本文使用的nanoFluidX软件是由德国慕尼黑的Flui-Dyna公司开发的一款基于SPH方法的GPU(图形处理单元)运算软件，主要用于预测在复杂几何体中有复杂机械运动的流动，GPU并行技术的使用提供了显著的性能优势，实现了快速高效的流体力学问题数值仿真。齿轮传动问题是该软件的主要应用领域之一，可以用于预测有旋转轴和齿轮的传动系统润滑并分析系统每个部件的力和力矩，并已有了相关成功应用案例[9]。

SPH计算方法起源于Colagrossi[10]和Mo -naghan[11]的相关研究工作，该方法使用一组粒子离散和代表所模拟的介质(流体或固体)，并且基于粒子体系近似和估算介质运动的控制方程。对于齿轮传动这种包含复杂几何运动的应用，SPH方法对比传统的网格方法来说具有几个明显的优势[12]。 (1) SPH方法作为一种粒子方法，运动过程中粒子数量不变，质量严格守恒； (2) SPH方法应用粒子代表所模拟的介质系统，避免大变形导致网格畸变，适合模拟大变形问题； (3) SPH是拉格朗日方法，能够自然地描述介质运动的历史过程，避免计算对流或输运项； (4) SPH方法可以在特定位置布置粒子，通过跟踪粒子的运动确定物质的运动，不需要复杂的算法来追踪诸如自由表面、移动边界及运动界面等运动特征； (5) SPH方法用粒子而非网格单元代表所模拟的系统，适合非连续介质的模拟。

2 SPH理论模型和控制方程

在拉格朗日框架下，等温流体的能量守恒自然满足，因此控制方程可以用连续性方程

(1)

和动量方程来描述，

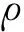
(2)

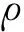
粘性力Fv可表示为

(3)

SPH粒子位置的更新遵循拉格朗日方法为

dx/dt=v(t)

(4)

本文采用弱可压方法对流体进行建模。假设模拟低声速的不可压流体，这样允许不超过1%的人工可压缩性。较低的声速放松了CFL时间步长的条件，可使计算效率显著提升。该方法不需要求解泊松方程，而是求解一个人工的状态方程来计算压力[13],

(5)

3 计算模型及结果分析

在利用NanoFluidX进行滑油泵数值仿真分析前，首先需要确定SPH粒子间距。在SPH方法中，粒子间距对计算结果的精度影响较大，粒子间距越小，计算精度越高，但同时计算效率也会随之下降。因此在正式计算之前，需要建立不同粒子间距的初始模型进行预计算，以确定能同时保证计算精度和计算效率的粒子间距。对于该齿轮泵模型，预计算结果表明0.5 mm的粒子间距足以保证计算精度和计算效率。对于齿轮泵进出口压力边界的施加，由于SPH方法直接给粒子施加压力容易造成计算不稳定，因此将采用以下两种方法构建压力边界。

(1) 周期模型。进出口设置周期边界。压力边界以进出口选定区域内设定强制加速度的形式给出，

(6)

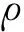
(2) inlet模型。入口生成具有初速的流体粒子，出口直接流出，入口压力由生成的流体粒子冲击入口预设挡板产生，具体大小可通过粒子初速调整。

3.1 周期模型

图3为周期模型在入口压强101 kPa、出口压强360 kPa和转速3185 r/min情况下，于稳定时刻获得的内部流体压强分布。

图3 周期模型压力分布

结合图2和图3可以看出，进出口强制力施加边界确定了油泵内部流体的稳定段，周期模型尽管在初始时刻填满壳体内部，但流体只在边界的限制段内达到平衡稳定。在进出口强制力施加区域内，检测进出口压力边界的施加情况，

入口： 97.15 kPa+Δ1

Δ1∈(-0.35 kPa，+3.47 kPa)

出口： 544.03 kPa+Δ2

Δ2∈(-1.51 kPa，+3.81 kPa)

与预设的进出口压力值之间偏差较小。且齿间的高低压区分明显，入口低压升高至出口高压。计算流量为15.72 L/min。随后,调整计算参数中的转速，获得相应流量，并与试验值对比如下。

由表1可知，模拟与试验值之间偏差极小，说明构建的周期模型能够准确进行滑油泵于中低速下的数值模拟。

表1 计算参数及流量结果

3.2 inlet模型

inlet模型需在图4入口位置设置流量入口，本文需要定义粒子的初始速度和位置。但流量入口生成的粒子并不直接流入泵内，而是冲击设置的挡板产生入口边界压力，推动其右侧布置的粒子进入泵内。该模型计算得到的流量为15.74 L/min。提取plate附近和出口强制力施加区域的压力，

Pplate: 100.15 kPa+Δ1

Δ1∈(-0.25 kPa,+1.31 kPa)

Poutlet: 546.35 kPa+Δ2

Δ2∈(-0.85 kPa,+2.91 kPa)

相较于周期模型，与压力边界的偏差更小。

图4 inlet改进模型的压力分布

进出口边界和压力边界设置的不同,使得两种模型在结构和计算效率上存在差异。表2给出粒子数与模拟时间的对比。

表2 两种模型对比

从粒子规模上看，inlet模型规模最大。原因在于inlet模型入口产生的流体粒子并未直接进入泵内，相反仅起到推动挡板的作用，因此需预计运转稳定段内的全部粒子，并将其预设在挡板右侧，造成模型整体规模最大。

从运算时间上看，周期模型较短。inlet模型规模大,造成运算时间增长。因此,从模型构建和数值模拟的角度，选择周期模型作为滑油泵仿真模型。

4 影响齿轮泵性能的参数

4.1 高转速流量分析

当齿轮泵结构一定时，泵的每转排量也随之确定，理论流量与转速的关系如下[14,15],

q=2πZbm2n

(7)

式中Z为齿数，b为齿宽，m为模数，n为转速。

利用上述构建的周期模型对滑油泵中低转速进行模拟，转速范围为637 r/min～3822 r/min，其余参数值不变，得到流量与转速的关系曲线如图5所示。

图5 周期模型-流量与转速关系

可以看出，流量与转速呈现较为严格的线性关系，这与式(7)给出的流量与转速关系十分吻合。但在试验中发现，随着转速的持续增长，流量会在高转速情况下出现数值的降低。

根据油泵运行原理，齿轮退啮合后形成局部低压环境，与外部压力形成的压差推动流体进入齿间，并随齿轮运转排除。但当转速过高时，内外压差无法驱动流动完全填满退啮合的齿间，使得齿轮容积效率降低，因而流量下降。为实现高转速时齿间未填满现象的模拟，需对周期模型进行适当调整。

假设油泵处于无穷大转速，此时齿间无流量传输，对于周期模型齿间亦无流体粒子分布。因此考虑初始便删除齿间粒子，预留内部空间以完成高转速模拟。综上，构建以下四种对比模型。

(1) 模型a。在内部填满的基础上，删除两个齿间布置的流体粒子4806/1071721(占总数0.448%)。

(2) 模型b。在内部填满的基础上，删除齿间布置的所有流体粒子31833/1071721(占总数2.97%)。

(3) 模型c。内部均匀减少一定数目流体粒子，不局限于齿间122008/1071721(占总数11.38%)。

(4) 模型d。在模型c的基础上，删除齿间所有的流体粒子138945/1071721(占总数11.97%)。

将上述四种模型在工况一条件下针对不同转速进行模拟，得到流量-转速关系如图6所示，并绘制出其结果趋势线作为参照。

图6 流量与转速关系

可以看出，在内部充满流体粒子的基础上，对模型进行删减粒子从而构建的模型能够对高转速工况进行模拟，理由如下。

(1) 转速8000 r/min时，四种模型得出的流量相较于线性数值已有略微降低，这说明构建的四种模型能够进行高转速模拟。

(2) 对于模型a，仅删除两个齿间的粒子时，模拟转速存在下降临界值，随着转速的升高，产生的未填充区域会大于预留区域。

(3) 对于删除粒子数大于或等于齿间总粒子数的模型b、模型c和模型d，高转速模拟的数值结果基本重合，且当转速为20000 r/min时，模型c和模型d依然可以完成仿真。

(4)当转速为10000 r/min时，模拟的数值结果和提供的参考值36.5 L/min的偏差在2%以内。

(5) 中低转速时，删除粒子并未对结果产生影响。原因在于进出口压力边界确定油泵内部稳定段，删除粒子后该范围内依旧存在足量粒子参与计算。

4.2 齿轮泵间隙泄漏分析

滑油的泄漏严重影响齿轮泵性能的充分发挥，而以端面间隙和径向间隙造成的泄漏为主要部分[16]。利用CFD解决油泵内部的微小间隙，因前处理网格构建复杂以及运算时间较长，给间隙模拟带来一定难度。本文基于SPH方法构建的粒子模型，通过构建大量模型端面间隙，获得对应的流量泄漏值，利用间隙泄漏的理论公式[17]反推得到对应的理论间隙，最终建立端面理论间隙与模型间隙的关系。图7给出模型中端面间隙，粒子间距为0.5 mm。构建多个模型间隙，得到相应泄漏量，列入表3。

图7 端面间隙

表3 端面间隙与泄漏量

利用泄漏量及模型确立的泄漏理论公式[18]，获得相应的理论间隙，拟合得到两种间隙的对应关系为

y=2789.1x3-740.8x2+66.8x-0.8

(8)

式中x为理论间隙，y为模型间隙。

利用现有的模型及理论公式构建的两种间隙的拟合关系，适用于粒子间距为0.5 mm的计算模型，旨在获得任意齿轮泵规则或不规则端面间隙与泄漏量的关系。径向间隙对应的关系式构建步骤与端面间隙相同。

4.3 空化现象分析

油液的空化会导致滑油泵性能和效率下降[19,20]，产生气泡，造成流量降低，同时还会产生振动和噪声，对齿轮泵造成损伤[21]。但粒子模型构建时，粒子的相态便已确定，无法在过程中实现气液转化。因此本文通过近似处理的方法，考虑饱和蒸气压对齿轮泵流量的影响。

图8中B为入口强制力施加位置，A点为齿轮泵吸油腔处。当模型确立后，流体由B至A沿程损失，造成压力下降。通过不同入口压力的模型，得到压降与入口压力的关系如图9所示。

图8 压差的求解

图9 压降与入口压力

由此已知B点入口压力值，便可确定A处的压力。考虑饱和蒸气压对流量的影响，即是通过判定A处压力值与饱和蒸气压值的关系。

(2) If:pB-Δp≤ps，判定无流体流入。

通过直接将饱和蒸气压减去的方式，近似考虑其影响，可体现出对流量的影响。但无法实现气液动态变化，同时夸大气化对流量的影响，因此只能作为对饱和蒸气压的粗略分析，整体的精确性还有待结合试验与模拟进一步研究。

4.4 齿轮扭矩分析

在检验泵的综合性能时，齿轮的扭矩也是一项重要指标。以往对于该问题的研究主要采用试验和经验分析相结合的方法，存在一定的适用范围和局限性。NanoFluidX软件可直接提取齿轮扭矩，从而可从数值计算的角度为该问题的研究提供新的思路。提取周期模型中不同转速下的齿轮扭矩值，结果如图10所示，可见扭矩与转速基本呈线性关系。

图10 扭矩与转速关系

5 结 论

基于SPH方法的仿真工具NanoFluidX软件，因其粒子法的特性，使其在解决复杂几何体中伴随复杂机械运动的流动具有较大的优势。本文将其应用在齿轮泵的数值研究中，得到了较好的研究结果。

(1) 通过初始模型的简化和边界的设置，得到了两种不同的粒子模型。两种模型在中低转速下获得的计算流量均与转速呈现较好的线性关系，且与试验值吻合良好。

(2) 通过适当调整周期模型初始布置的流体粒子，删除内部填充的部分流体粒子，可在不影响中低转速模拟结果的前提下进行高转速滑油泵的数值仿真。

(3) 为了获得径向端面间隙与泄漏量的关系，通过构建大量模型端面间隙的方法，获得相应泄漏量，并利用理论公式建立了模型与理论间隙的对应关系。

(4) 为了在计算模型中加入空化现象，提出了将饱和蒸气压值加入边界压力设置的近似处理方法。

(5) 对不同转速下的齿轮扭矩计算结果进行了提取，初步发现扭矩与转速基本呈线性关系，与试验结果的对比有待进一步研究。

致谢:感谢中国航发哈尔滨东安发动机有限公司对本研究提供的无私帮助。