一种基于双前沿推进的边界层网格生成算法
2022-03-10刘田田董庆利冷珏琳郑澎
刘田田, 董庆利, 杨 洋, 冷珏琳, 郑澎
(1.中物院高性能数值模拟软件中心,北京 100088; 2.北京应用物理与计算数学研究所,北京 100094;3.中国工程物理研究院计算机应用研究所,绵阳 621900)
1 引 言
高雷诺数绕流仿真模拟中存在紧贴壁面的粘性力不可忽略的流动薄层,即边界层。在边界层内,物理量梯度变化很大,为了提升模拟精度,要求边界层内的网格尽量垂直于壁面。目前,分块结构网格和混合网格是粘性计算中常用的两类网格。分块结构网格采用分而治之的策略,将模型分解成若干个子块,每个块内生成结构化网格。这类网格的正交性好,但对于复杂外形,需要花费大量的时间进行子块分解,操作非常繁琐。混合网格在边界层采用半结构化的三棱柱单元,剩余区域采用四面体单元填充。半结构化的边界层网格在垂直于壁面方向具备结构化特征,能很好捕捉边界层的粘性流动特征;在平行于壁面方向具备非结构化特性,能灵活地适应复杂几何外形。这两类网格的边界层网格生成都是粘性模拟过程中的难点问题,吸引了众多学者的关注和研究。
分块结构网格的边界层网格生成方法有两类,一类是基于表面网格,利用双曲方程或椭圆方程等生成边界层网格,如商业软件Pointwise等,这类方法无法自动处理边界层网格相交的情况,需人工一层一层生成。另一类是在拓扑分区时预留出边界层的子区域,利用超限映射等方法生成初始网格,再对网格进行正交性优化,如商业软件ICEM等,这类方法面向复杂几何外形时,增加了人工分区的难度和工作量。卢风顺等[1]提出一种适用于飞机的分块结构网格边界层拓扑自动生成方法,该方法对表面网格进行几何特征提取,根据几何特征构造边界层网格框架,基于超限插值方法在边界层网格框架内生成边界层网格。该算法在一定程度上提高了分块网格生成的自动化程度,减少了拓扑分区的工作量。
经过数十年的发展,适用于混合网格的边界层生成算法研究已经取得了很多成果[2-17]。然而,对于复杂几何外形的边界层网格生成,至今没有形成完善的解决方案。目前,混合网格边界层网格生成方法有如下三类。
(1) 局部前沿层进方法。局部计算前沿点的法向和步长,逐层生成边界层网格。这类方法是目前研究最广泛的一类方法,发展了可视锥[2]、最优法向[7,18]、多法向[3]、法向合并[5]、步长缩减[19,20]和自动缩层[15,21]等多种技术处理局部细小特征和凹凸特征。
(2) 四面体聚合方法。在边界层附近生成各向异性四面体网格,然后合并四面体得到三棱柱网格[16,22]。
(3) 全局前沿层进方法。整体计算新前沿的位置。一种是将前沿的推进过程转化成物理量传播的过程,通过求解PDE方程得到下一层前沿的位置[10]。另一种是利用水平集方法整体推进前沿[9,23]。
目前混合网格的边界层网格大都是利用三角形生成三棱柱单元,实际上这类方法同样适用于四边形生成六面体单元。分块结构网格的表面网格拓扑分区可以看成是一个非结构四边形网格,因此,混合网格边界层的网格生成方法可以用于分块结构网格边界层拓扑分区的生成。分块结构网格的一类边界层生成方法是在拓扑分区内进行结构网格细分,这种思想也可以用于混合网格边界层的生成。因此,混合网格的边界层网格生成方法和分块结构网格的边界层网格生成方法可以互相借鉴,形成优势互补。受文献[1,20]方法的启发,在已有研究成果的基础上,本文提出了一种双前沿推进思想,综合采用多种技术处理局部几何特征,形成了一种边界层网格生成算法。
2 算法概述
双前沿推进过程中,存在标架前沿和参考前沿两套数据。标架前沿是需要生成边界层的前沿,参考前沿可以是更密的网格也可以是几何,用来辅助标架前沿在推进过程中进行相交检测。如图1所示,在分块结构网格中,标架前沿是表面的拓扑分区,参考前沿是表面网格或几何数据。在混合网格中,标架前沿是待生成边界层的表面网格,参考前沿可以是加密的表面网格,如果参考前沿和标架前沿使用同一套网格,则等同于以往的混合网格边界层前沿推进算法。因此,双前沿推进算法可以看成是局部前沿层进算法的扩展。
基于双前沿推进的边界层网格生成算法流程如图2所示,算法的输入、输出和具体流程如下。

图2 双前沿推进边界层网格生成流程
输入:标架前沿、参考前沿、边界层的第一层高度、相邻层之间的过渡比以及总的边界层层数等。
输出:边界层网格。
流程: (1) 构建标架前沿和参考前沿;(2) 计算标架前沿点的法向;(3) 计算标架前沿点的步长;(4) 光滑化标架前沿点的法向和步长;(5) 判断标架前沿中是否存在相交,若存在相交,调整标架前沿点的法向或步长,若不存在,执行下一步;(6) 插值计算参考前沿点的法向和步长;(7) 判断参考前沿中是否存在相交,若存在相交,调整标架前沿的法向或步长,执行(6),若不存在,执行下一步;(8) 生成一层边界层单元,判断边界层单元是否有效,如网格单元质量、单元是否反转等;(9) 根据需要细化边界层单元;(10) 优化边界层网格单元质量。
与传统的局部前沿层进方法相比,双前沿推进算法不仅考虑当前待推进前沿的特征,还考虑了更精细的几何特征,其优势主要包括两个,(1) 将局部前沿层进算法从混合网格推广至分块结构网格,可同时适用于分块结构网格的边界层生成和混合网格的边界层生成。将结构网格的表面分区看成是非结构网格,利用双前沿推进算法可以有效提升生成结构网格分区拓扑中边界层分区构建的自动化程度。(2) 由于考虑了更精细的特征,能有效避免因网格离散精度不够导致的边界层位置不合理。
3 边界层网格生成
3.1 标架前沿点的法向计算
最传统的方法采用相邻单元的法向平均作为前沿点的生长方向,但在尖锐特征附近极易产生反转单元。文献[2]提到,不产生反转单元的一个必要条件是前沿点的生长法向与点连接的所有单元都是可见的,即法向在可视锥范围内,如图3所示。设点P周围的面单元集合为Fp,面单元的法向分别为Nj(j∈Fp)。三角形单元的法向取其外法向方向,对于四边形单元,首先将其划分成两个三角形,单元的法向取两个三角形法向的平均值。对每个前沿点,可视锥定义为[2]
{M∈R3|PM·Nj>0,∀j∈Fp}
(1)

图3 可视锥
可视锥本身是一个多面锥,为了简化,可以用圆锥来替代。文献[7]的最优法向技术可以保证计算出的法向在可视锥范围内。最优法向的计算方法是,极小化法向与周围单元法向的最大夹角。该问题的求解可以转化为点集的最小覆盖圆问题,其中两点之间的距离定义为球面距离。有定理表明,最小覆盖圆一定会穿过点集的两个或至多三个点。由于每个前沿点周围的面个数一般在4~8个左右,可以采用枚举的方法求解该问题。计算所有过任意两点或三点的覆盖圆,筛选其中半径最小的圆,该圆心与P点的连线方向就是前沿点的法向。
图4(a)给出了利用最优法向计算得到的前沿点的初始方向。这种方法对一般的几何外形可以满足,但是对于有凹角的外形,在凹角处很容易网格相交。为了减少凹角处的网格相交,采用加权的Laplacian平滑算法对法向进行平滑,
(2)

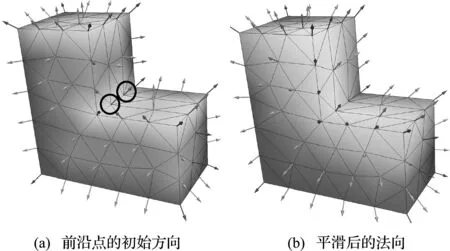
图4 标架前沿点法向

表1 平滑前后凹角点的最大步长
3.2 标架前沿点的总步长计算
边界层的第一层高度记为h1,相邻层之间的过渡比为t,总的边界层层数为n,则计算出边界层的初始总高度为
(3)
为减少前沿相交,首先利用射线法计算每个前沿点的最大可行步长。为节省计算量,采用R-Tree对前沿单元进行空间位置分割。基于R-Tree和单元的碰撞检测技术,计算从前沿点Pi出发沿法向方向Ni长度为2h的线段是否与其他前沿相交,若相交,则计算第一个交点Qi与Pi之间的距离,记为前沿点Pi的最大可行步长,hmax(i)=|PiQi|,否则,hmax(i)=2h。根据最大可行步长,重新计算每个前沿点的步长为
(4)
前沿面以波阵方式向前推进时更有利于凹凸特征附近生成光滑的前沿面,从而提高网格单元质量。因此,在凹角点附近减小步长,凸角点附近增加步长,像吹气球一样使步长平滑过渡。凹凸角点的判定方法参见文献[15]。根据凹凸性计算步长的公式为
(5)
式中βi为前沿点的特征角,取Pi邻接的所有边二面角的平均值,
(6)
dihedral(lj)为Pi邻接的第j条边相邻两个面的二面角。
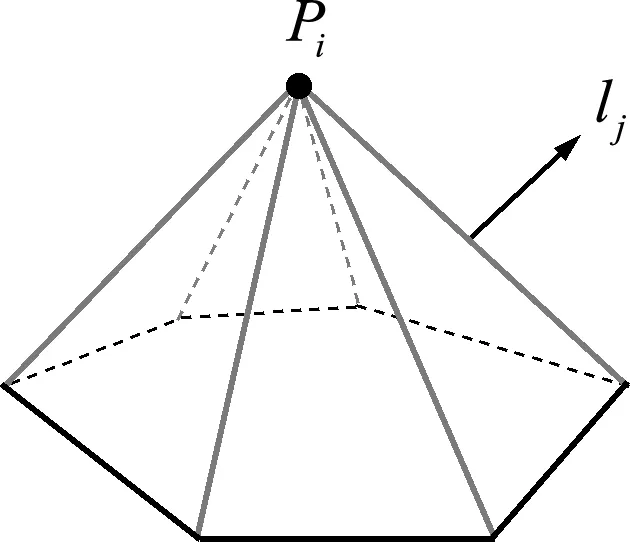
图5 特征角
图6给出了一个立方体分别向内和向外生长边界层时的步长。向外生长时立方体边上的点是凸点,图中步长明显缩减,向内生长时立方体边上的点是凹点,图中步长明显增大。为了避免相邻点之间的步长相差过大导致单元畸形,对前沿点的步长进行Laplacian平滑,
(7)
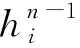

图6 凹凸特征步长
3.3 标架前沿相交性检测
为了避免标架前沿生成网格时产生相交问题,需检测前沿推进后在空间中是否相交,并据此调整标架前沿点的步长。采用R-Tree空间搜索树对数据进行空间分割,从而提升数据搜索效率。具体算法流程如下。
(1) 将标架前沿的原始前沿面和推进后的前沿面进行三角化。
(2) 构建所有三角形单元的空间包围盒搜索树。
(3) 对每一个推进后的前沿面,利用搜索树查找与其包围盒相交的单元,采用三角形碰撞检测判断是否存在实际相交。若相交,则缩短其包含的前沿点的步长,直到不再相交,h″(i)=ε·h′(i),其中ε为步长收缩因子,取值[0.5,1.0)。对于无法通过步长缩减避免相交的前沿单元,局部调整其包含的前沿点的法向,再进行相交检测,直到不再相交。
3.4 参考前沿相交性检测
将计算参考前沿的每一个前沿点投影到标架前沿,计算投影点相邻的标架前沿点,根据这些点的法向和步长插值计算参考前沿点的法向和步长。为了避免复杂特征处,由于网格离散精度不够导致的边界层网格不合理的问题,判断参考前沿点推进后是否会存在空间相交。相交性检测的方法同 3.3 节相同,如果参考前沿单元相交,需缩短标架前沿点的步长,并重新计算参考前沿点的步长,直到参考前沿中不存在相交。
3.5 单元有效性检测和修正
确定前沿点的法向和步长,可以获得一层总的边界层单元。为了避免产生质量非常差的单元,判断这一层总的边界层单元中是否存在无效或质量差的单元。判断网格质量的标准是计算单元的Jacobian值和扭曲度。Jacobian值若为负值,表示单元反转。扭曲度在一定程度上能表征与理想单元的偏离程度,定义如下,
(8)
式中θe为面单元或体单元的等角,θmin和θmax为面单元或体单元的最小角和最大角。对于体单元,计算偏斜度时,采用skewness=max{Surface(skew),Volume(skew)},其中Surface(skew)为体单元包含的所有面单元的偏斜度,Volume(skew)为利用体单元二面角计算出的偏斜度。
对于Jacobian异常或扭曲度差的单元,缩短其包含的前沿点的步长或局部调整法向,直到所有单元质量达到要求。
3.6 边界层单元细化
对于分块结构网格,标架前沿推进后得到的每一个单元都是边界层的一个拓扑子块。在每个拓扑子块内,根据边界层参数要求,采用超限映射方法(TFI)对边界层网格进行细化,再将网格点投影到真实的几何。对于混合网格,得到一层总的边界层网格后,根据边界层的层数和过渡比,计算每个前沿点对应的每层边界层单元的高度,将总的边界层细分成指定层的边界层网格。记前沿点Pi的总步长为h*(i),则Pi对应的每层边界层单元高度为
(9)
3.7 边界层网格优化
分块结构网格的边界层网格可以采用带源项的椭圆方程进行网格正交性优化。混合网格的边界层网格采用文献[9]的能量函数法改善边界层单元的质量。三棱柱的能量函数定义可以推广到六面体网格,利用采用棱边单元的正交性能量函数E⊥(τ)和底面单元的形态能量函数Eθ(τ),定义单元的质量能量如下,
E(τ)=μEθ(τ)+(1-μ)E⊥(τ)
(10)
式中μ为底面单元形态与棱边正交性之间的权重比重。优化网格质量的方法是极小化所有单元的总能量,
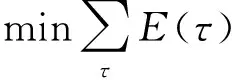
(11)
利用拟牛顿迭代求解该极小化问题。
4 数值实验
输入前沿后,给定边界层第一层的高度、层高的过渡比和总的层数,可以自动生成边界层网格。以下实例中,混合网格的表面网格为三角形或四边形单元,远场网格采用四面体单元。分块结构网格的边界层内采用TFI生成初始网格,再用椭圆优化进一步优化网格质量。图7给出一个简单球体的网格生成效果,包含了混合网格和多块结构网格的边界层网格,验证了双前沿推进算法对两类网格的适用性。

图7 球体模型边界层网格
图8给出了三维翼型模型的混合网格和多块结构网格结果。翼型区域内表面设置为壁面。从图8(a)可以看出混合网格的边界层过渡非常平滑,单元形态规整。图8(b)左图是翼型模型的拓扑分区,将该拓扑分区映射到几何模型后生成多块结构网格,如图8(b)右图所示。
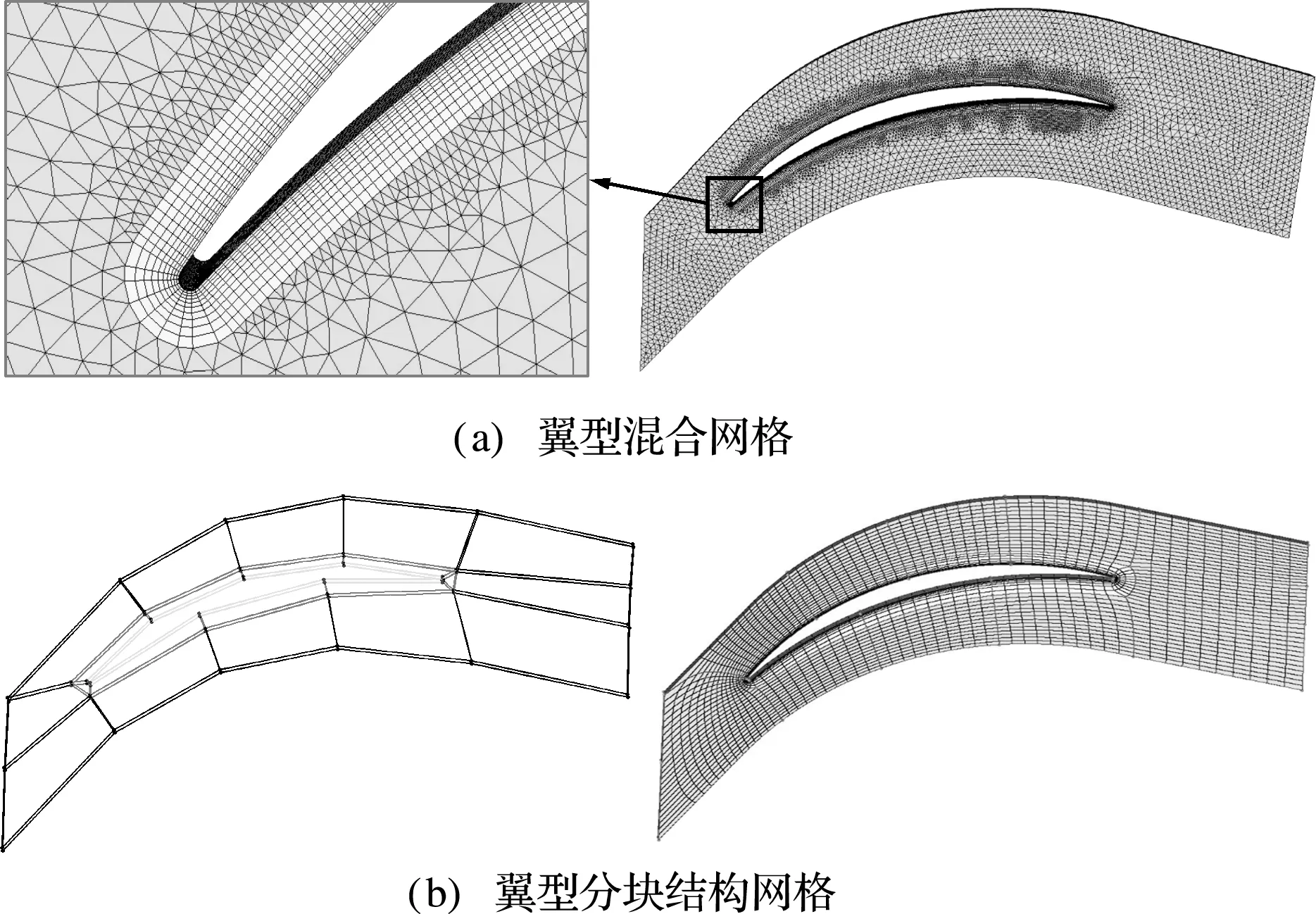
图8 翼型模型
为了进一步验证算法的有效性,对F6模型进行了混合网格剖分,如图9所示。图10对边界层网格的扭曲度进行了统计。可以看出绝大部分边界层网格质量都很好,但包含非常少量的扭曲度大于0.9的单元,这也是后续要继续研究的问题。

图9 F6模型混合网格

图10 F6混合网格质量统计
5 结 论
本文面向粘性流体模拟的边界层网格生成问题,提出了一种双前沿推进思想,并发展了一种同时适用于分块结构网格边界层生成和混合网格边界层生成的算法。为了适应复杂几何特征,算法综合采用了最优法向技术、步长调整技术和极小化能量优化网格等关键技术。测试算例表明了该算法的有效性,但对复杂模型在凹凸特征附近会产生少量质量差的单元,这是下一步研究工作的重点。
