相似集合预报技术在粤西风场预报中的应用

何泽锋，薛宇峰，张宇，龙景超，张树钦，郑福涛，魏晓钰，郑美盈，田霖

（广东海洋大学海洋与气象学院，广东湛江 524088）

相似集合法（Analogue Ensemble，AnEn）是结合相似理论、气象观测资料与模式资料，对气象资料或数值预报产品进行分析、解释和误差修正的一种统计释用方法［1］，应用于相同地点、相同起报时刻、相同预报时效的模式订正。相似集合法采用了大数据的统计分析与预报集合思路，在模式订正方面具有较为稳定的特点［2-4］，也是目前较为新颖的一种订正释用技术［5-6］。在全球气候变暖的背景下，极端天气事件频发导致的气象灾害以及引发的次生灾害发生发展趋于严重［7］，更加突显了模式后处理的可靠、高效和准确在预报业务中绝对的重要性［8-9］。粤西地区三面环海，丘陵区域地形条件复杂，又恰好处在南亚季风与东亚季风交汇之地，风速风向复杂多变，预报难度极大；同时，由于探测、同化等多方面存在的不足，数值预报误差较大［10-11］，尤其对沿岸测站的预报误差随风力增大趋于显著［12］。本研究以粤西10 m风速作为预报对象，采用相似集合方法来建立粤西地面风场订正预报模型，为改进粤西地区风的预报提供参考。

1 资料与方法

1.1 相似集合法

对于任一个需要订正的气象要素，找出与该气象要素相关性较大的若干气象因子，利用这些因子来构成相似集合模型。相关性大小可籍公式（1）计算环境场的相似程度来判断：

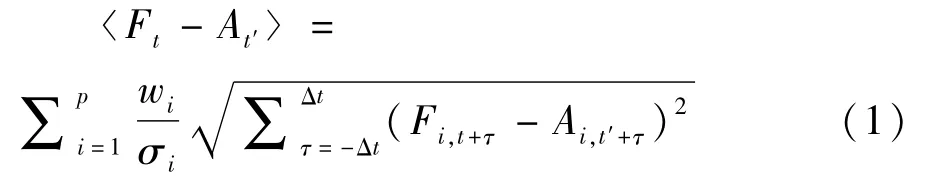
其中，t为变量订正的时刻，而t′为某一历史时刻；Ft是t时刻确定性的模式环境场；At′为在与Ft相同位置上t′时刻的模式环境场；p是选取的相似因子个数；σi是第i个因子历史时间序列的标准差；Fi，t＋τ和Ai，t′＋τ是第i个因子分别在t和t′时刻要素的值；wi是相似因子的权重。式（1）表示在t时刻某一要素场前后Δt时段内与历史某一t′时刻要素场在前后Δt时段内的相似程度（前后Δt时间段长度称为时间窗长度），采用时间窗长度可以考虑到要素场在这一时间窗内持续变化的相似性，使得式（1）能描述要素场对于一段时间内持续演变过程，而式（1）中根号下Fi，t＋τ-Ai，t′＋τ的平方和 可视 为两要 素场之 间 的“距离”。“距离”越短，表示这两个时刻的要素场相似程度越高。假设历史数据样本集足够大，那么利用该公式可以找到与Ft相似的若干个历史t′时刻的要素场At′，若干个相似的历史要素场则可以利用集合预报的思想计算得出对应要素的确定性要素值，即获得订正后的模式数据。选取其中n个“距离”最小、相似程度最大的历史t′时刻的要素场At′，然后利用式（2）与t′时刻对应要素的气象观测值一并来计算订正后确定性的模式数据FANEN：

其中，n是相似成员数。

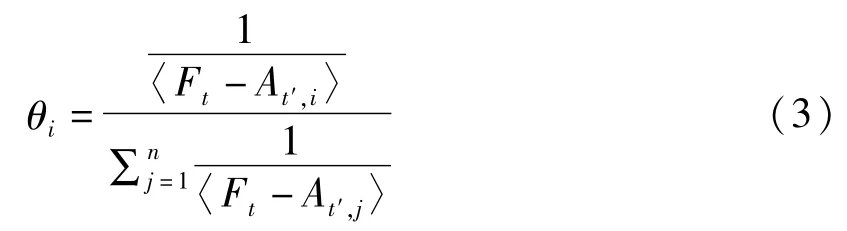
其中，〈Ft-At′，i〉为式（1）中计算出n个需订正时刻t与t′时刻的历史要素场“距离”最小的结果；Oi为对应要素场的观测值。

1.2 资料

使用2017年1月1日—2018年12月31日共计730 d逐时ERA5再分析资料，插值到粤西17个地面站点上（图略），计算得到10 m风的逐日平均风速与最大风速，以此730 d的平均风速与最大风速作为需要订正的两个要素。以2017年1月2日—2018年12月30日逐日风速（Δt＝1）作为需要订正t时刻，同时选取2007年1月2日—2016年12月30日逐日ERA5资料作为历史t′时刻通过式（1）计算相似度，从中得出n（本研究n＝20）个相似集合成员，结合对应历史t′的观测资料通过式（2）得出订正后逐日平均风速与最大风速。

参照王在文等［4］研究成果并考虑天气学意义，分别选取与风速相关性较好的3个物理量作为相似度判据的因子（即式（1）中p取3）：海平面气压、2 m气温、平均风速和最大风速。

2 订正结果与检验

2.1 检验指标

均方根误差：

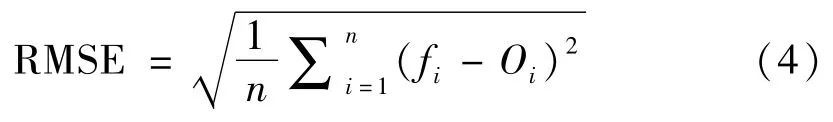
订正偏差：

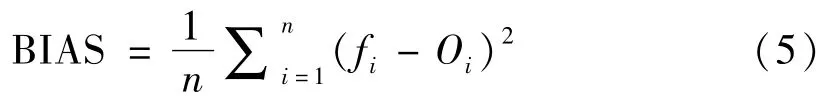
其中，n为需要订正的时次；fi为第i个模式的值；Oi为第i个站点的观测值。均方根误差的数值直接反映订正数值的精确程度，而订正偏差反映出订正的偏差程度。

2.2 空间分布检验

粤西地区17个站点2017年1月2日—2018年12月30日平均风速的空间检验结果显示（图1），ERA5的均方根误差均大于0.68 m/s，最大为2.30 m/s，在海岸线附近的站点均方根误差都较内陆站点的要大得多，而在平原地区的均方根误差相对较小。化州站均方根误差最大（12.01 m/s），分析发现化州站在此期间的历史资料中相似成员数较少，引入了相似程度不高的要素场，导致订正误差显著偏大。在后续的数据处理以及讨论中剔除该站点。除去化州站，经过AnEn订正后的平均风速均方根误差总体不超过0.88 m/s，且在靠近海岸线的几个站点订正效果尤为显著，平均均方根误差减少率为41.84%，最高达72.25%。而平均风速经过AnEn订正后偏差接近0 m/s。

图1 粤西地区17个站点2017年1月2日—2018年12月30日平均风速的订正检验

ERA5资料计算的最大风速（图略）具有较高的均方根误差，各站点基本都在1.50 m/s以上，最大值为2.47 m/s。经AnEn订正后，均方根误差都降到了1.63 m/s以下，最小降为0.96 m/s。吴川站出现了负的均方根误差减少率，可见AnEn对该站最大风速订正无效。除去吴川站以外，最大风速的平均均方根误差减少率为23.02%，减少率最大达到38.03%。对比可见，AnEn方法对于最大风速的订正效果没有平均风速的好，而对于最大风速来说ERA5的值普遍偏小，最大的偏离程度达到了-1.71 m/s，而在最大风速经过AnEn订正后偏差程度也接近0 m/s。

2.3 时间顺序的效果检验

通过建立相似集合模型，构建起2017年1月2日—2018年12月30日日平均风速与日最大风速的相似集合订正成员集。为了判断该相似集合订正成员集的订正效果与稳定程度，对订正后的日平均风速与日最大风速进行检验。

对平均风速总样本全部日数计算逐日均方根误差（图2a），总体上看，经过相似集合订正后的AnEn集合在日平均风速的均方根误差明显要小于ERA5资料。ERA5的日平均风速均方根误差日变化大，最小0.2 m/s，最大达到了3.9 m/s；AnEn的日平均风速均方根误差几乎稳定在0.5 m/s以下且日变化小。ERA5的日平均风速均方根误差大概在8月中旬—9月上旬出现最大误差（图2b），而在6、7月份均方根误差相对较小；AnEn的日平均风速均方根误差无明显季节变化，全年相对稳定。

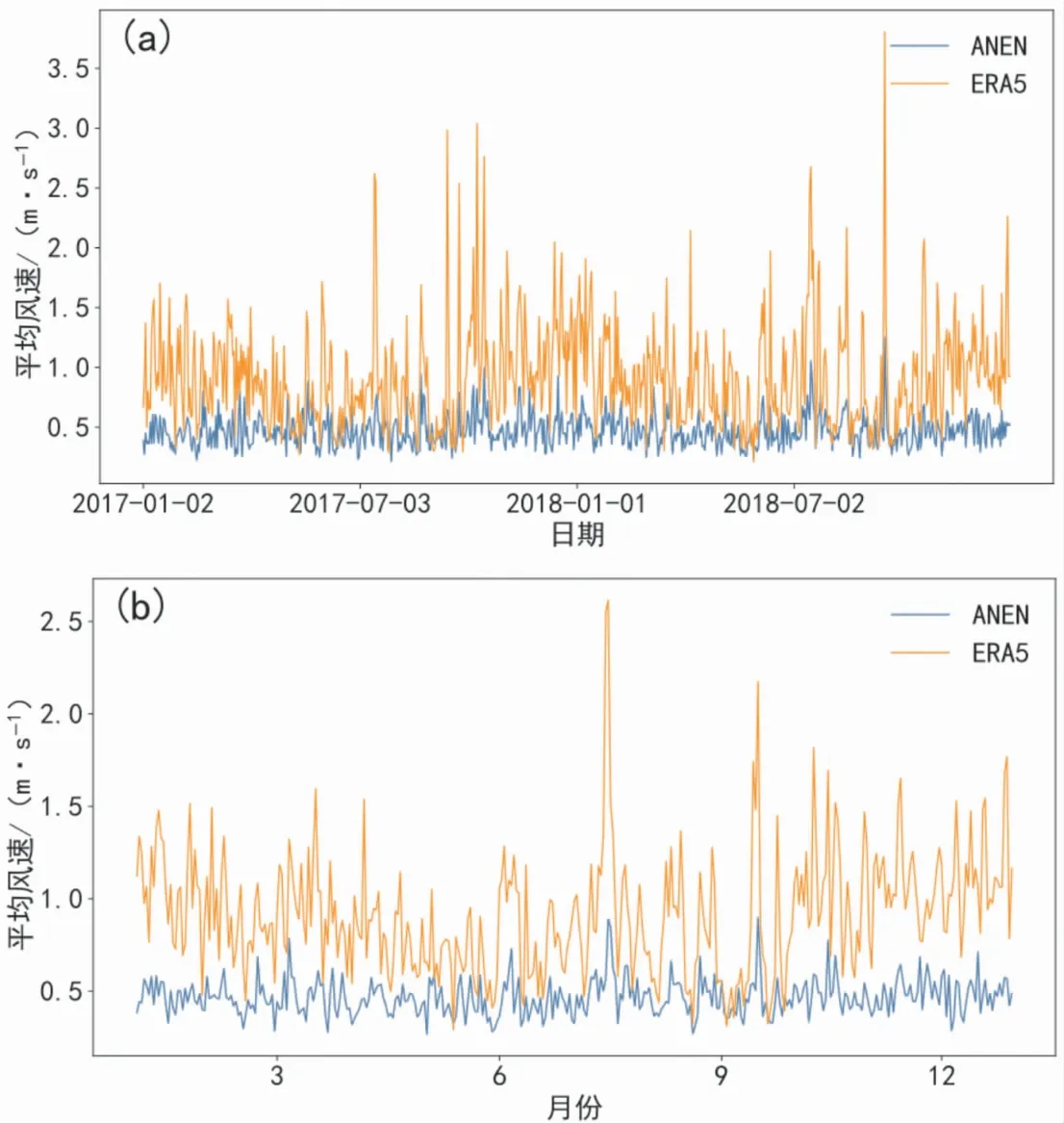
图2 平均风速的均方根误差检验

不管是ERA5资料还是AnEn资料的日最大风速的均方根误差明显要比日平均风速的误差大（图略）。ERA5的日最大风速均方根误差都在0.3 m/s以上，最大接近6 m/s，波动非常大；AnEn的日平均风速均方根误差曲线中存在某几天的误差极大，这可能是由于在相似集合模型中与该几天相似形势场的天数较少。但AnEn的日平均风速均方根误差除去个别几天存在极大的误差之外，总体的AnEn日平均风速均方根误差小于ERA5资料，说明AnEn对日最大风速的订正还是比较好的。ERA5再分析资料日最大风速的均方根误差有较为明显的季节变化，11月中下旬到次年4月份均方根误差比5—10月的均方根误差要小且相对稳定，基于ERA5资料订正的AnEn数据，其日最大风速的均方根误差有着和ERA5再分析资料相似的季节变化，其波动变化也较为相似。在季节变化总体上看，相似集合的订正还是比较有效的。

3 集合性能评估

3.1 相似集合各成员逐日均方根误差

在式（2）各历史相似成员为加权平均和，若要分析单个成员与实际风速的均方根误差，必须修改公式形成新的相似集合成员与实际风速进行对比。此处公式简化为

即只考虑订正时刻的要素场和与之相似的历史要素场之间的相似程度，忽略其相似程度对订正结果加权平均的影响。在所研究的17个站点中，每个站点均有20个相似成员，即一天共有340个成员。

相似集合的订正对于日平均风速与日最大风速来说，日平均风速的异常值数量要远小于日最大风速（图3），而且其相似集合成员相对日最大风速来说也更为集中。以3—5月代表春季、9—11月代表秋季，对比两个季节的日平均风速，在春季各相似集合成员的均方根误差要优于在秋季。而对比春秋季日最大风速，并无明显的季节性变化。总体来看，不管是日平均风速还是日最大风速，其各相似集合成员的日均方根误差与相似集合的日均方根误差（蓝色实线）较为接近，各相似集合成员还是比较接近订正后的结果。

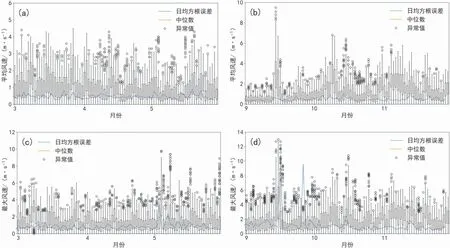
图3 相似集合各成员3—5月（a、c）和9—11月（b、d）日平均风速（a、b）与日最大风速（c、d）的均方根误差

3.2 集合离散度和集合平均方根误差

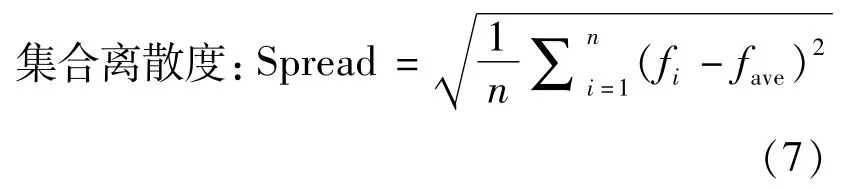
其中，n为相似集合成员数；fi为相似集合各订正成员的大小；fave为相似集合各订正成员的平均值。集合离散度（总样本的离散程度）检验的是相似集合成员对订正要素的稳定性和离散的偏差，而集合平均方根误差检验的是相似集合成员的准确度。集合离散度和集合平均误差越接近，表示集合离散度越能够代表系统的误差演变特征，集合系统越可靠［13］。

图4对比了日平均风速与日最大风速的集合离散度和集合平均均方根误差。日平均风速和日最大风速的集合离散度都较小于集合平均均方根误差，同时日平均风速较日最大风速要更为集中，集合平均均方根误差要更小，说明日平均风速更为稳定和准确。虽然日最大风速的集合平均均方根误差波动较大，但是总体上来看，不管是日平均风速还是日最大风速的集合离散度和集合平均均方根误差还是比较相近的，说明相似集合系统较为可靠。

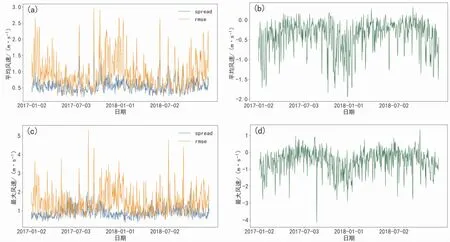
图4 总样本天数日平均风速与日最大风速集合离散度与集合成员平均的均方根误差（a、c）及集合离散度与集合成员平均的均方根误差之差（b、d）

4 结论

基于ERA5再分析资料，采用相似集合法对粤西地区地面日平均风速与日最大风速进行订正，研究相似集合法在粤西地区的适用性，探讨其在空间上订正效果以及集合成员的性能。

1）利用相似集合法对粤西地面风场的日平均风速与日最大风速进行误差订正后，空间检验效果显著。日平均风速和日最大风速在各个站点上误差都有明显减小，且在复杂地形的山区也有较好的订正效果，个别站点效果不理想。日平均风速的误差平均减少率为41.84%，而最大风速的误差平均减少率为23.02%，日平均风速的订正效果优于日最大风速。

2）ERA5与AnEn的逐日均方根误差曲线显示，ERA5的日平均风速的均方根误差要小于日最大风速，且波动更小更为稳定。基于ERA5再分析资料订正的AnEn，误差波动较为相似，对于更为稳定误差更小的日平均风速做出的订正，AnEn中日平均风速的订正效果也要优于日最大风速。AnEn的日平均风速全年误差波动较小，无明显起伏，也没有明显的季节变化，而日最大风速全年误差波动较为剧烈，在5—10月的误差比其他月份误差更大。

3）对于各成员离散度分析中，日平均风速的相似集合成员相对日最大风速来说更为集中。日平均风速的相似集合成员在春季比秋季集中，而日最大风速在春秋季没有明显差异。两者的集合离散度和集合平均均方根误差大部分都比较相近，说明集合系统较为可靠。日平均风速的集合离散度和集合平均均方根误差更为接近，说明日平均风速更为稳定和准确。

总体而言，相似集合法在粤西地面风场的日平均风速与日最大风速订正中有较好的释用效果。但存在个别站点或者个别天数误差较大的情况，或许可从调整相似因子的选取、相似成员数n和采用更庞大的数据集来减少误差，获得更为良好的数据订正集合，有待进一步深入探讨。