基于神经网络自适应算法的机械臂位置/力控制
2022-03-10王泰华马彬彬李亚飞
王泰华,马彬彬,李亚飞
(河南理工大学 电气工程与自动化学院,河南 焦作 454003)
0 引言
机械臂在许多领域有着不同的应用,如航空、医疗、农业、工业等[1-4]。在工业生产中的抛光、打磨等加工工艺,要求机械臂施加指定的力并沿指定的轨迹移动,这就需要做到位置和力同时控制。此外,机械臂是一个参数未知且变化的非线性对象,存在外部干扰、摩擦以及非线性耦合等,所以此类系统仍有许多问题有待解决。
为了解决机械臂动力学模型中不确定参数和外部扰动,文献[5]提出了一种基于模糊滑模控制,通过将模糊算法与滑模控制相结合,解决了在不确定环境下机械臂力/位置混合控制问题;文献[6]提出了一种模糊PID 滑模控制器,该方法实现了对冗余机械臂末端轨迹的精确跟踪,提高了冗余机械臂位置控制时对模型不确定性和外部干扰的鲁棒性;文献[7]提出了一种基于自适应PID 算法的位置/力控制,实现了工作空间下的位置/控制。但文献[5-7]所使用的方法无法满足工作空间下存在外界干扰和建模误差等不确定因素的情况。因此,本文设计了一种基于神经网络自适应算法的机械臂位置/力控制方法。
1 问题描述
机械臂动力学模型可以描述为[8-9]

将m维工作空间分解机械臂与环境接触时的法向r维接触力空间和切向m-r维位置空间,故可写为

2 控制器设计
2.1 RBF神经网络
RBF 神经网络是一种前馈式神经网络,可对任意未知非线性函数进行逼近,其结构[12]如图1 所示。
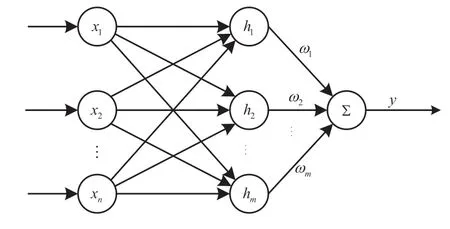
图1 RBF神经网络结构
RBF 神经网络算法表示为

2.2 控制器

控制器结构如图2 所示。
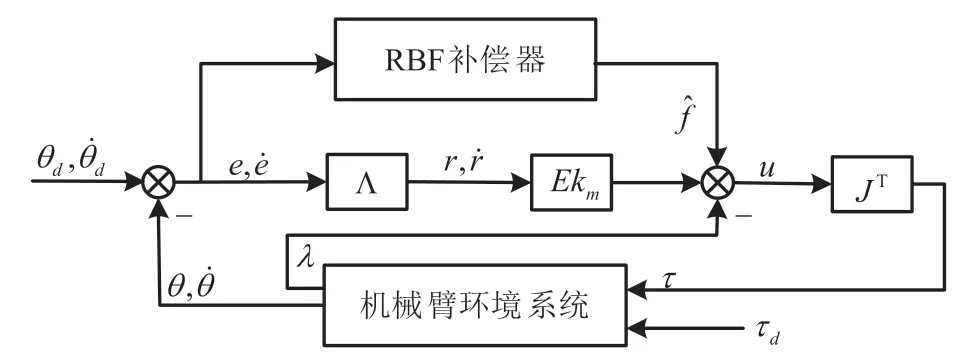
图2 控制器结构图
设计控制律为

设计神经网络自适应律为

2.3 稳定性分析
设计Lyapunov 函数为
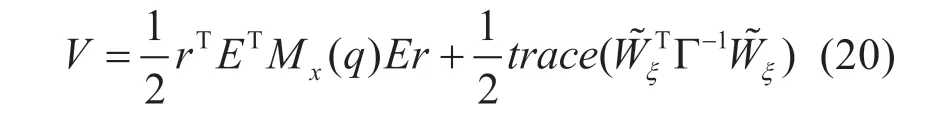
式(20)对时间求导,并由假设2 和式(18)得

3 仿真实验
3.1 仿真参数设定
为了验证控制算法的有效性,选择二连杆机械臂系统进行仿真。其动力学方程为式(1),系统结构如图3 所示。

图3 机械臂系统
机械臂参数如下:

3.2 仿真结果分析
基于上述参数设定,以PID 方法设计对比实验,取仿真时长为10 s,仿真结果如图4~图7 所示。
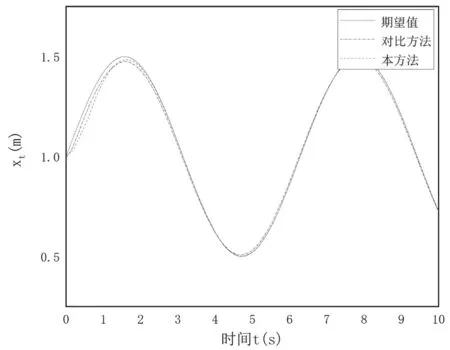
图4 切向位置
图4 为切向位置的期望值、实际值和对比值,图5 为法相接触力的期望值、实际值和对比值,图6 为不同方法与期望值的位置误差,图7 为不同方法与期望值的力误差。由图6 和图7 可知,补偿系统经过短时间的学习可以快速跟踪到期望值,滑模面在有限时间内收敛。根据图6 和图7 可知,在0.5 s 后位置实际值误差接近零,较对比方法快了约2.5 s;在0.2 s后接触力误差接近零,较对比方法快了约0.2 s,且更稳定。
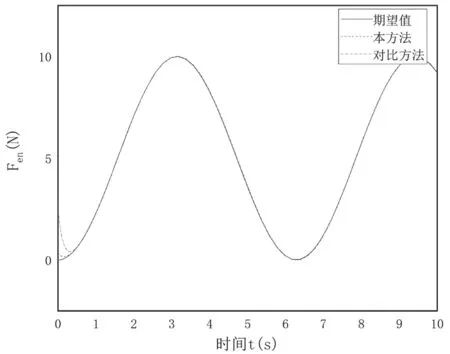
图5 法向接触力
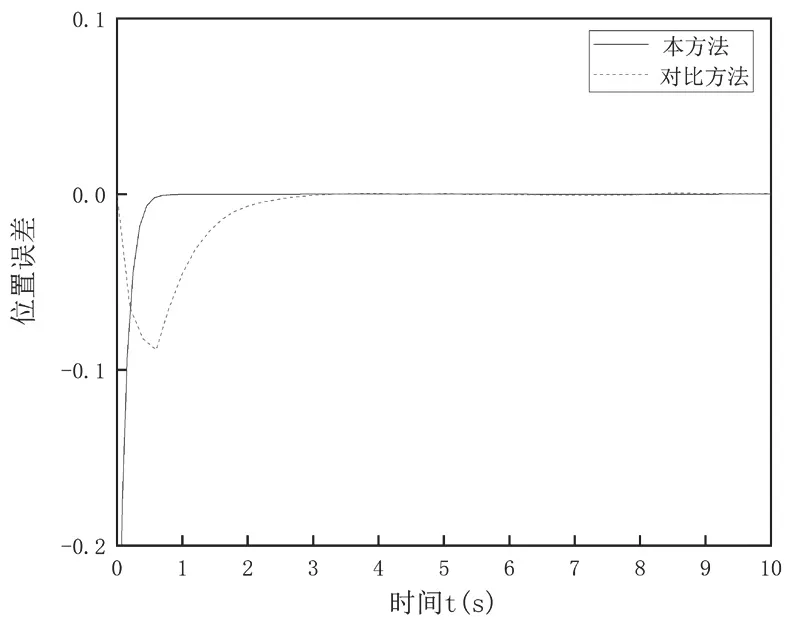
图6 位置误差

图7 接触力误差
综上结果表明,在满足一定条件下,本文所设计的系统可以对模型中的非线性、不确定部分进行补偿且具有良好性能,验证了理论的有效性。
4 结语
本文设计了一种基于神经网络的位置/力控制系统。利用RBF 神经网络对不确定项进行逼近,补偿控制器,实现了工作空间下存在不确定因素时的机械臂力/位置控制。设计仿真模型并与PID 自适应算法进行对比,仿真结果表明,系统可在有界干扰以及建模误差下具备良好性能。
