轴向磁通三相感应电机的优化设计

上官璇峰，贾晓路，杨恒宇

（河南理工大学 电气工程与自动化学院，河南 焦作 454003 ）

0 引言

轴向磁通感应电机（Axial Flux Induction Motor，AFIM）具有轴向尺寸短小、结构紧凑、散热性好、可靠性高、效率高、材料利用率高、转动惯量小等特点，曾因为加工技术和生产工艺等问题，受到一段时间的冷落。随着科学技术的进步与生产生活的需要，近年来受到越来越多的关注[1-3]。国外对AFIM 研究起步早，且在不断发展与完善，我国相比之下不足之处还有很多。AFIM 在电动汽车、数控机床、风力发电、混合动力汽车等领域有广阔的应用前景[4-7]。AFIM 存在三维模型建立与运行所需时间长、计算量大的问题，目前AFIM 常用的研究方法有平均直径法与分环法，文献[8-10]表明在计算、仿真、分析AFIM 时，采用分环法相对于平均直径法具有较高的准确性。文献[11-13]表明T 形等效电路可作为分析AFIM 稳态特性的有效工具，可转化解决AFIM 存在的三维模型建立与运行所需时间长、计算量大的问题。

田口法通过建立正交实验，能在最少的实验次数内搜寻出多目标优化的最佳组合；响应曲面法为一种建立近似响应面模型的统计方法，通过实验或模拟得到的结果获取响应值与变量参数之间的数学关系；田口法与响应曲面法被广泛应用于电机的多目标优化设计领域。

本文以一台三相单边鼠笼式AFIM 样机为例，旨在提高其额定运行时的功率因数、效率与电磁转矩，降低其能量的浪费，利用T 形等效电路求解电机稳态结果，避免三维模型建立与运行时间长，计算量大等问题；分别采用田口法、响应曲面法对电机进行了优化。

1 AFIM结构参数优化

AFIM 与传统径向磁通感应电机的工作原理相同，最主要的区别是其磁场方向为轴向与定、转子铁心为盘状；三相单边鼠笼式AFIM样机结构如图1 所示，其由一个盘形定子与一个盘形转子组成，定、转子之间是盘形气隙，定、转子铁心均开槽，定子绕组与鼠笼绕组分别放在定、转子槽内。三相单边鼠笼式AFIM 的主要参数见表1，其定、转子槽形如图2 和图3所示。

图1 三相单边鼠笼式AFIM结构图

表1 三相单边鼠笼式AFIM主要参数

图2 定子槽

图3 转子槽

1.1 田口法

在田口法正交实验中，选取定子槽宽bs1、定子槽口宽bs0、转子槽口宽br0为变量参数，每个变量选取3 个水平；保证电机起动性能、定子槽满率等约束条件，合理选择优化变量的取值范围；选取电机额定运行时的功率因数cosφ、效率η、电磁转矩Te为优化目标，参数及因子水平配置见表2。

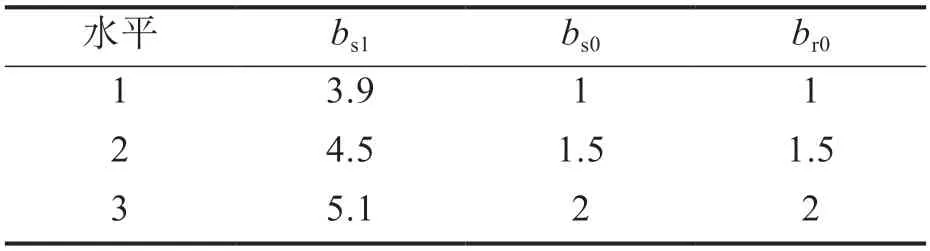
表2 优化变量及其水平配置 mm

正交实验选取3 个影响因子为变量，每个变量因子的水平为3，按照传统优化单一变量的优化方法，需要进行33=27 次，利用田口法只需要进行9 次，可降低时间成本。由于AFIM 存在三维模型求解不易实现等问题；本文利用解析法与有限元法相结合计算电机的定子电阻Rs、定子漏抗X1σ、折算后转子电阻R'r、折算后转子漏抗X'2σ、励磁电阻Rm、励磁电抗Xm参数(见表3)，在求解励磁电抗时，采用了分层模型，将分层模型工作于空载状态，利用有限元法求解出的反电势、铁耗值等进行相应计算得到，利用T 形等效电路(图4)求解电机稳态结果[14-16]，得到正交实验表4。采用二维有限元法(平均直径法)求解电机稳态结果，对比两种方法求出的电机稳态结果，得到图5、图6 和图7。

图4 T形等效电路

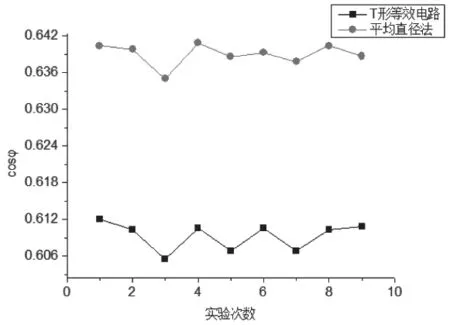
图5 功率因数对比

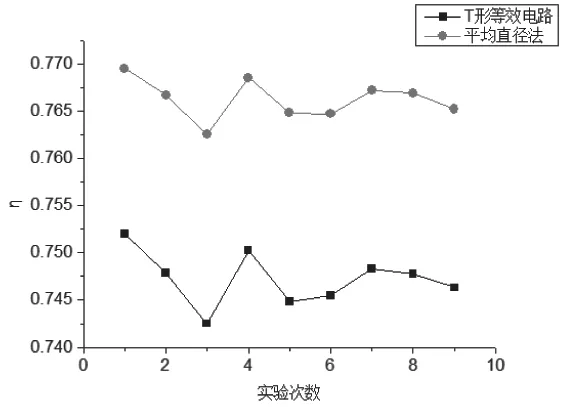
图6 效率对比

表3 电机电磁参数 Ω

表4 正交实验矩阵及求解结果

由图5～图7 可以看出，两种方法求出的电机稳态结果变化趋势几乎一致，在一定程度上表明了T 形等效电路求出电机稳态结果的正确性。

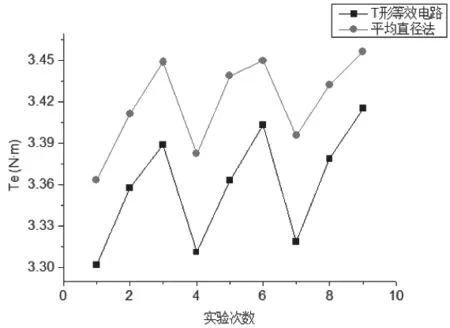
图7 电磁转矩对比

采用T 形等效电路求出的电机稳态结果略小于平均直径法，原因在于：

1)平均直径法是以电机整体为研究对象，忽略气隙磁密、饱和系数等参数沿径向的变化，相应参数均取其平均直径处数值；

2)采用T 形等效电路求解稳态结果时，需先求出T 形等效电路所需的电磁参数，解析法求解电磁参数可能存在误差。

对正交实验表4 中求出的电机稳态结果进行平均值(式1)、方差(式2)计算：

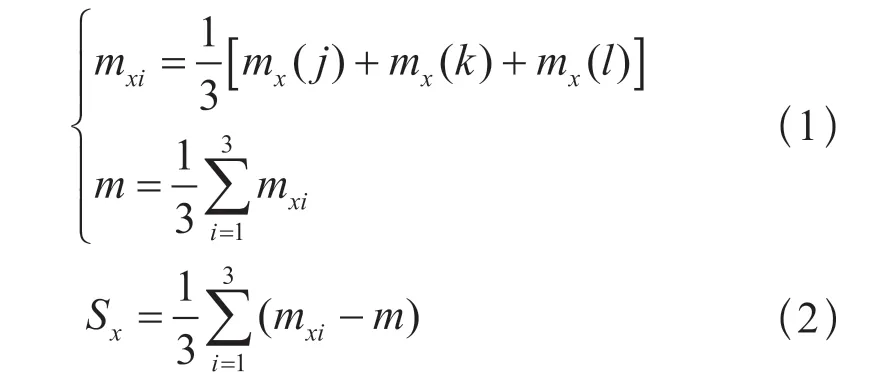
其中，mxi为变量参数x的第i水平值相对应的某一优化性能指标的平均值；mx(j),mx(k),mx(l)为变量参数x的第i水平值相对应的各实验下的某一优化性能指标，j、k、l为实验序号；m为变量参数x的各水平值的某一优化性能指标的平均值；Sx为变量参数x相对应的某一优化性能指标的方差值；x为变量参数(bs1,bs0,br0)。

不同变量参数在不同影响因子水平下优化性能指标的平均值与方差值见表5，将表5 中数据进行整理得到图8、图9 和图10。求出各参数变化对目标性能的影响比重，影响比重的占比结果见表6。

由表5～表6 以及图8～图10 可以看出，考虑到不同水平下目标性能的平均值变化趋势与变量参数改变对目标性能的影响，选取bs1=5.1，bs0=2，br0=1 为田口法优化结果。

表5 各变量参数因子水平对应的目标性能平均值、方差值

表6 变量参数对目标性能的影响

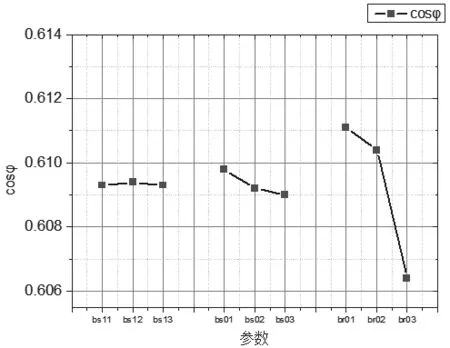
图8 各参数不同水平下电机功率因数的平均值

图9 各参数不同水平下电机效率的平均值

图10 各参数不同水平下电机电磁转矩的平均值

2 响应曲面法

由于田口法只是在统计上有意义，并不保证最少实验次数就能得到最佳结果。故采用响应曲面法求取定子槽宽bs1、定子槽口宽bs0、转子槽口宽br0与电机额定运行时优化目标之间数学模型，响应曲面法设计矩阵、电磁参数与求解结果见表7 和表8。采用二维有限元法(平均直径法)求解电机稳态结果，对比两种方法求出的电机稳态结果，得到图11、图12 和图13。

图11 功率因数对比

图12 效率对比

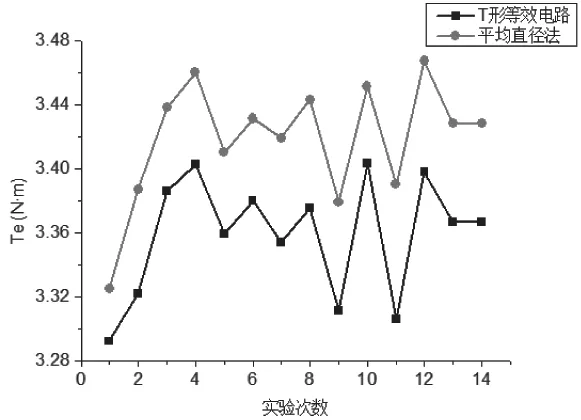
图13 电磁转矩对比

表7 电磁参数 Ω

表8 响应曲面法设计矩阵求解结果

由图11～图13 可以看出，采用T 形等效电路与二维有限元法(平均直径法)求解电机各次稳态结果趋势变化几乎一致，此处不在赘述存在差异的原因，在一定程度上表明了采用T 形等效电路求出稳态结果的正确性。采用T形等效电路求出稳态结果，求出各优化目标与各变量参数之间的一个近似数学模型，其回归方程如下（式3）。

其中bs1∈[3.9,5.1]；bs0∈[1,2]；br0∈[1,2]，由田口法求出的不同水平下优化目标平均值的变化趋势（图3～图5）可知，各优化目标存在相互影响；对于AFIM 而言，额定运行时其功率因数、效率与电磁转矩是望大的；对三个优化目标给予相同的权重，求解公式3 得到一系列优化结果，见表9，尽可能大的提高功率因数、效率、电磁转矩，选取响应曲面法优化结果为(bs1,bs0,br0)=(3.9,1.54,1)。

表9 响应曲面法优化结果

3 优化结果对比

利用T 形等效电路分别将响应曲面法、田口法得到的优化结果与优化前数据进行对比，得到表10。采用二维有限元法(平均直径法)求解了电机稳态结果，对比了两种方法求出的电机稳态结果，得到图14、图15、图16。由表10 可以看出，采用田口法优化的结果，电磁转矩增大，功率因数与效率稍微降低。采用响应曲面法优化的结果，功率因数些许提高，电磁转矩增大，效率稍微降低。由图14、图15、图16 可以看出，采用T 形等效电路与二维有限元法(平均直径法)求解电机稳态结果趋势变化几乎一致，在一定程度上表明优化结果的正确性。由于三维有限元法实现困难，本文未利用三维有限元法验证优化结果。

表10 优化前后对比

图14 功率因数对比

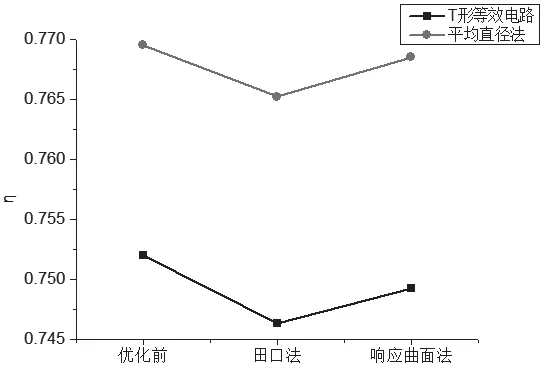
图15 效率对比

图16 电磁转矩对比

4 结语

本文将田口法、响应曲面法应用到轴向磁通感应电机优化过程中，计算出电机电磁参数，采用T 形等效电路求解电机稳态结果，避免了三维模型存在的建立与运行所需时间长以及计算量大等问题，分别利用田口法与响应曲面法对电机进行优化。采用二维有限元法求解电机稳态结果，对比两种方法求出的电机稳态结果，分析了存在差异的原因，利用T 形等效电路与二维有限元（平均直径法）将优化前、后额定运行时电机的功率因数、效率、电磁转矩进行了对比，各次稳态结果趋势变化几乎一致，在一定程度上表明了优化方法的正确性。