基于柱坐标抛物方程的海上雷达覆盖范围研究

汪路遥 邓小川 廖成 杨巨涛 冯菊

（1. 西南交通大学电磁所，成都 610031；2. 中国电波传播研究所 电波环境特性及模化技术重点实验室，青岛 266107）

引 言

复杂海洋环境如大气波导、粗糙海面、降雨降雾等多种因素对雷达波传播有着重要的影响[1-3]，因此准确构建海上电波传播预测模型，对海洋环境中的电磁态势进行预测和分析，在雷达远距离目标探测、识别、跟踪以及海上通信等领域具有重要意义[4-6].

抛物方程(parabolic equation，PE)模型是一种高效的电波传播预测模型，最早由Leontovich和Fock提出[7]. 该模型既能处理非均匀媒质带来的折射效应，又能处理复杂地表引起的绕射效应，在远距离复杂环境下具有较高的计算精度；结合分步傅里叶变换还可实现快速求解，计算效率高. 目前该模型已被广泛用于大区域复杂环境下的电波传播预测[8-10]. 美国军方基于传统直角坐标PE模型开发了高级折射效应预警系统(Advanced Refractive Effects Prediction System, AREPS)[11]，用于模拟复杂环境下的电波传播特性，对雷达系统性能进行评估.

然而基于直角坐标的传统三维PE(three dimensional PE, 3DPE)模型受近轴传播条件限制，只能计算特定扇形区域，一般为偏离传播主轴方向约30°方位角内的电波传播问题[12]. 且在大区域传播计算问题中，需要划分数量庞大的网格，因此计算效率较低.2005年，R.S.Awadallah等人提出基于二维剖面构造的准三维PE(quasi-three dimensional PE, Quasi-3DPE)模型，分析对流层雷达波的传播特性[13]，较3DPE模型大幅提高了计算速度，但由于忽略了水平方位面的绕射效应，精度较低.

针对上述问题，本文提出基于柱坐标PE(cylinder PE，CPE)电波传播预测模型，采用径向非均匀扇形网格，一次计算即可实现波源电磁能量的全向辐射特性. 该模型克服了3DPE模型水平剖面计算角度受限的问题，同时有效地考虑了电波横向绕射效应的影响，是雷达覆盖范围研究分析的有力工具. 论文首先对柱坐标PE传播模型的正确性进行验证. 然后结合具体的海洋环境，对海面的电波传播特性进行计算和分析. 最后基于雷达方程，评估了海洋环境雷达的有效探测范围. 仿真结果对海上雷达探测性能评估具有重要的参考价值.

1 柱坐标PE模型

PE模型是电波传播损耗预测的一种确定性模型，可体现电波的折射和绕射效应，在大区域环境下具有较高的计算精度和效率.

设电磁场时谐因子为 e−jωt，则柱坐标系下的亥姆霍兹方程[14-16]为

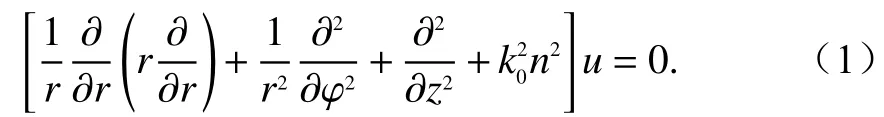
式中：k0为 真空中的传播常数；n为空间媒质的折射指数；u为传播空间中的电场. 采用分离变量法，电场通解可表示为三个正交方向基函数的乘积，即

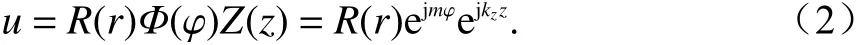
将式(2)带入式(1)可得径向基函数的支配方程

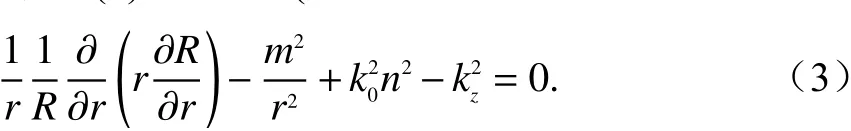
在柱坐标系下，若电波沿高度z方向传播，径向基函数满足贝塞尔函数形式；若电波沿径向传播，则应采用汉克尔函数形式. 由于本文分析雷达波在方位面的全向传播问题，即电波沿径向传播的情况，因此采用后者. 解式(3)，并忽略后向传播项，可得前向PE的解为

式中：am,kz为 各模式的激励系数；为m阶 第一类汉克尔函数. 可利用三角函数的正交特性，采用空间傅里叶变换进行数值求解[16]，得CPE模型迭代公式如下：

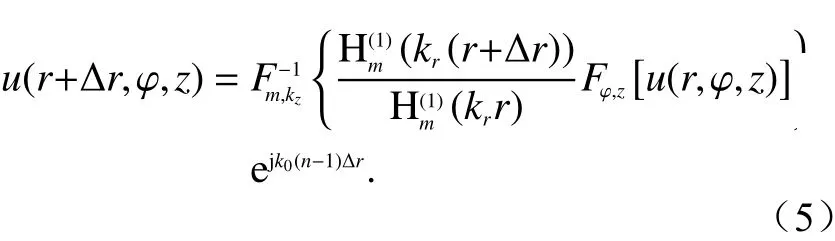
2 柱坐标PE模型验证和性能分析

为了对柱坐标PE模型的正确性进行验证，本文采用矩量法(method of moments, MoM)、3DPE模型和Quasi-3DPE模型分别对典型场景进行了仿真分析，并与CPE模型计算结果比较. 仿真算例如下.

算例1：八木天线的辐射场空间分布. 频率为0.3 GHz的八木天线置于距地表高6 m的位置. 天线增益方向图如图1所示.

图1 八木天线增益方向图Fig. 1 Yagi antenna gain pattern

分别利用MoM、CPE模型和3DPE模型计算电波传播100 m处电场随高度的变化曲线，结果如图2所示. 可以看出，直射波和反射波的相互干涉产生了波峰和波谷，三种方法计算所得场强曲线吻合较好，证明了CPE模型在高度向的正确性. 图3为传播距离100 m处，接收天线高度为6 m时，电场随方位角的变化曲线. 可以看出：CPE模型和MoM结果基本吻合；而3DPE模型的横向计算受到角度限制，仅在近轴小角度30°内与MoM结果吻合良好，超过50°时由于横向截面设置吸收边界条件，电场强度急剧衰减. 可见，CPE模型突破了传统3DPE模型计算方位角上的限制，具有全向性的优点，且具有较高的精度.

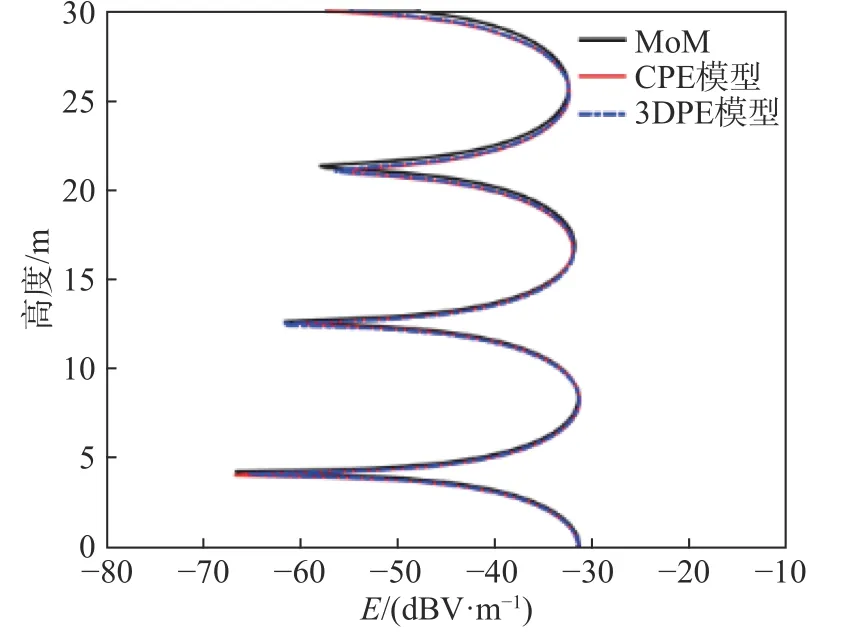
图2 传播距离100 m处电场随高度的变化Fig. 2 Variation of electric field with height at 100 m of propagation distance

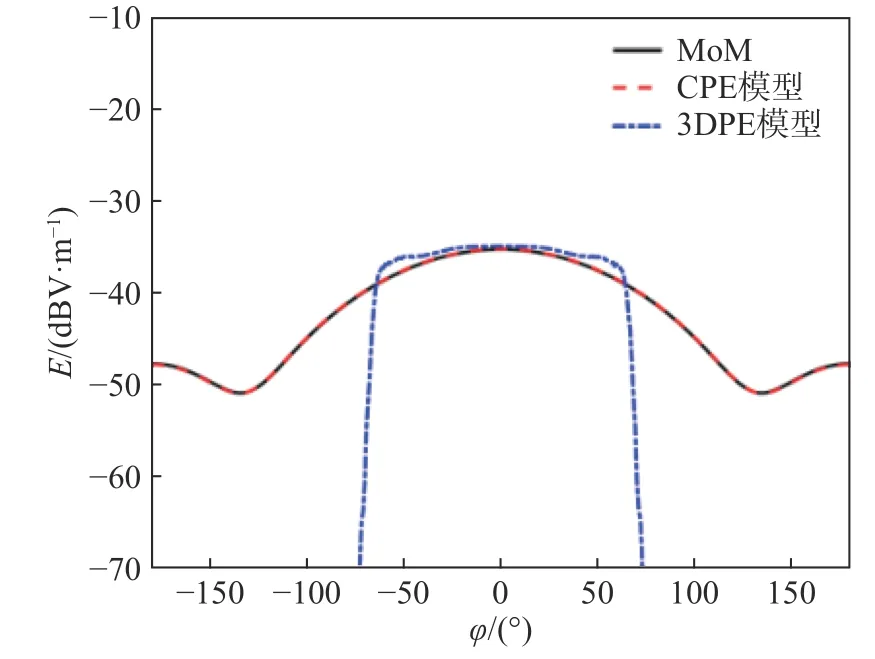
图3 传播距离100 m接收天线高6 m处电场随方位角的变化Fig. 3 The variation of electric field with azimuth at the propagation distance of 100 m and the height of 6 m

算例2：存在障碍物空间的辐射场分布. 设辐射源频率为0.3 GHz，高度4 m，在传播距离35 m处有一个长宽高分别为10 m、20 m、16 m的长方体型障碍物. CPE模型和Quasi-3DPE模型在仅考虑有物体遮挡的半空间中，计算所得电场的空间分布如图4所示. 可以看出：图(a)障碍物后方存在部分能量，侧后方出现了明显的干涉条纹，表明CPE模型考虑了电波的横向绕射效应；图(b)是Quasi-3DPE模型的计算结果，由于其实质还是二维方法，忽略了横向绕射效应，障碍物阴影区信号强度基本为零. 图5给出了接收天线高度分别为2 m、4 m、15 m时，电场随方位角的变化. 可以看出，未考虑电波在障碍物后方的绕射效应，Quasi-3DPE模型的计算误差随着高度的增加而增大. 表1为两种算法在相同剖分网格数量情况下的计算时间对比，可以看出Quasi-3DPE模型与CPE模型计算时间相当，仅快6 s，但其以损失计算精度为代价.

表1 两种模型计算时间对比Tab. 1 Comparison of calculation time between the two methods

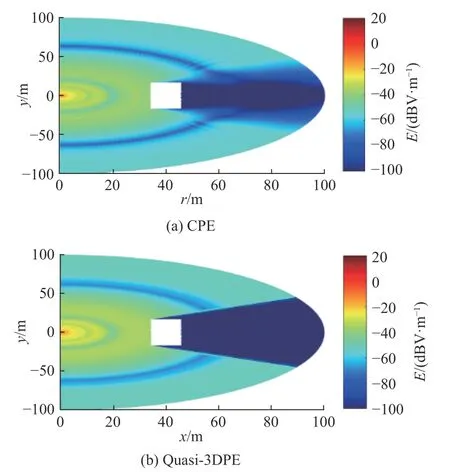
图4 CPE和Quasi-3DPE模型的电场分布伪彩图Fig. 4 Pseudo color diagram of electric field distribution of CPE and Quasi-3DPE

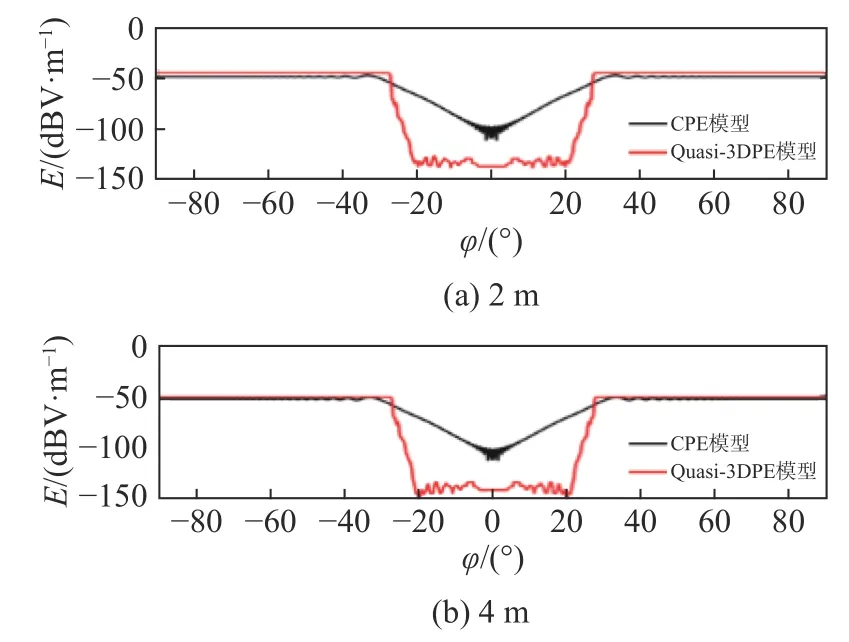
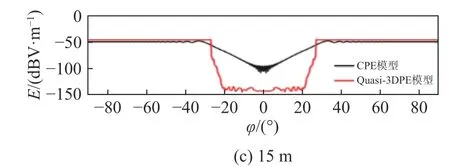
图5 不同高度处电场随方位角的变化Fig. 5 The change of electric field with azimuth angle at different heights

算例3：为了验证CPE模型处理非均匀大气的有效性，利用CPE模拟分析表面波导条件下的电波传播特性，其修正折射率如图6所示. 天线置于距地表50 m的高度，其频率为3 GHz采用波瓣宽度为3°的高斯方向图. 图7为CPE模型和3DPE模型垂直剖面电场伪彩图，两者电场分布趋势吻合很好，同时也可以看出：1)大气波导对电波具有明显的陷获作用，在波瓣临界角处发生分裂，且小于临界角的电波能量集中在波导层内不断向前传播，实现了电磁波的超视距传播特性；2)沿着波导层顶部，电波能量损耗较大，极易出现探测盲区. 图8为传播距离150 km处电场随高度变化曲线. 可以看出，CPE模型和3DPE模型计算结果吻合较好，进一步验证了本文提出的CPE模型能有效处理不同大气折射效应.

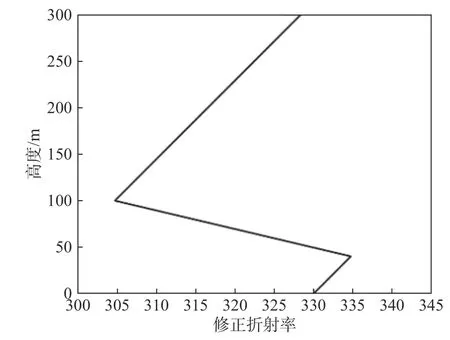
图6 表面波导修正折射率Fig. 6 Surface waveguide modifies refractive index

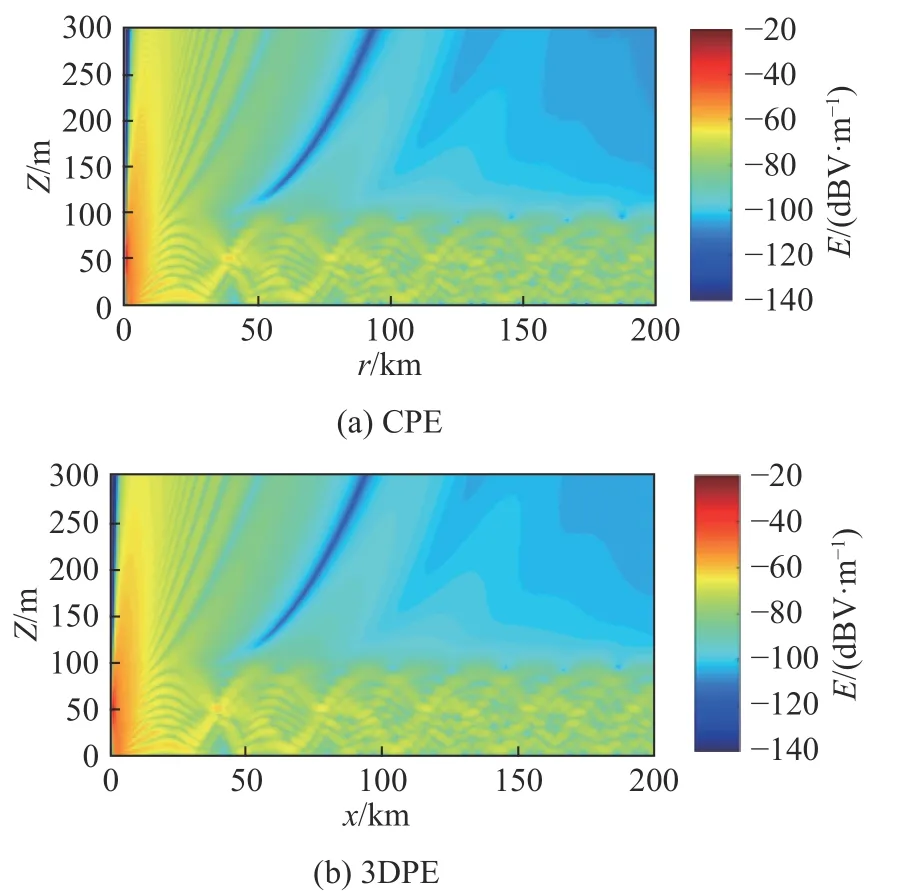
图7 φ=0°时垂直剖面内电场分布伪彩图Fig. 7 Pseudo color diagram of electric field distribution in vertical section φ=0°

图8 传播距离150 km处场强随着高度变化曲线Fig. 8 The curve of electric field intensity at 150 km of propagation range varies with height

3 雷达探测性能分析

依据文献[18]，雷达最小可检测信号的损耗门限值为

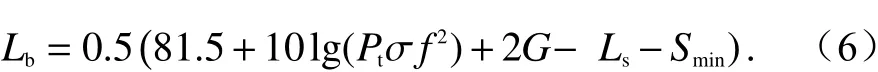
式中：Pt为雷达发射功率； σ为目标反射截面；G为收发天线增益；f为天线发射频率；Ls为系统带来的损耗；Smin为雷达最小可检测信号电平.

由CPE模型计算得到的损耗为LPE(r)， 当Lb≥LPE(r) 时 ，对应距离r内的目标能被雷达监测到，此区域即为雷达有效探测范围.

本节应用CPE模型分析海上波导环境、起伏海面对雷达波传播特性的影响，研究雷达的有效覆盖范围. 其中粗糙海面采用改进的分形模型模拟波动起伏的实际海况，海面风速为8 m/s. 蒸发波导高度为40 m. 发射天线高度为20 m，频率为2.8 GHz，方位面全向辐射，采用垂直极化方式. 假设雷达接收机的目标雷达散射截面积(radar cross section, RCS)为100 m2，由式(6)可得最小损耗门限为134 dB.

图9为方位角为0°时的电波损耗分布图. 可以看出波导层内电波损耗较小，实现了电波的超视距传播，最远传播距离处的损耗为135 dB，比标准大气的损耗减少了120 dB，有效探测范围显著增加.

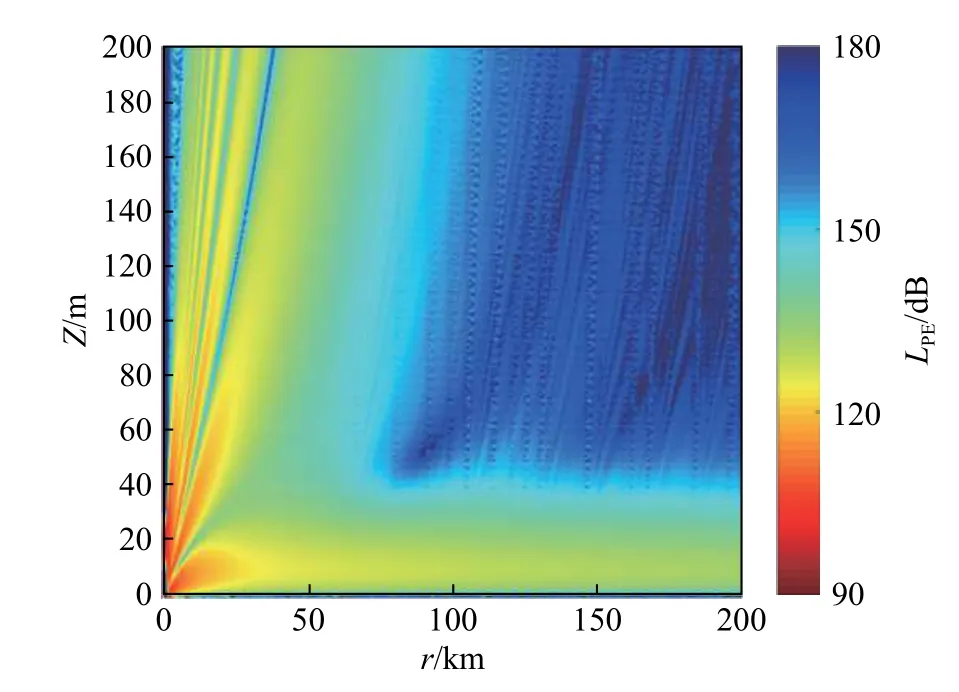
图9 φ=0°时电波损耗分布伪彩图Fig. 9 Pseudo color diagram of electromagnetic wave loss distribution in vertical section φ=0°

结合雷达方程，从图10可以得到雷达在20 m高度处的最大探测范围，由于蒸发波导的超折射条件，电波能量覆盖范围远大于标准大气环境.

图10 雷达探测距离Fig. 10 Radar detection distance

海上环境复杂多变，为定量研究不同风速对雷达能量覆盖范围的影响，图11给出了风速为0m/s、15m/s、30m/s时的雷达探测威力图. 可以看出，随着风速增大，海面粗糙度增加导致电波损耗增加，探测范围减小.

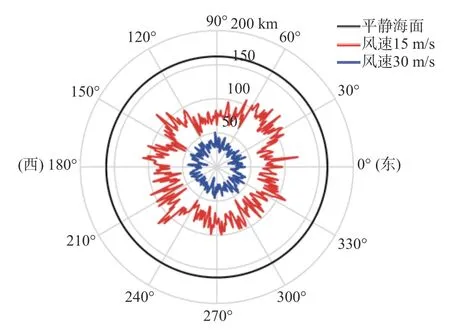
图11 风速对雷达探测距离的影响Fig. 11 Influence of wind speed on radar detection distance

此外，图12给出了不同波导高度下的能量覆盖情况. 其中收发射天线高度为10 m，发射频率为2.8 GHz，风速均为8 m/s. 从图12可以看出，在一定条件下，波导高度越高，陷获能力越强，在波导内部能量储存越多，雷达探测范围越大.

图12 波导高度对雷达探测距离的影响Fig. 12 Influence of waveguide height on radar detection distance

4 结 论

本文主要提出了基于柱坐标PE的电波传播预测模型，对海上雷达的全向传播特性进行研究. 在亥姆霍兹方程的基础上，推导了柱坐标系下的前向PE分步傅里叶解法. 与传统的3DPE模型相比，该模型突破水平方位角30°内近轴传播的限制，实现了电磁能量的全向特性计算，同时拥有比Quasi-3DPE模型更高的计算精度，特别适用于海上雷达波的探测性能分析. 最后结合实际情景，考虑大气波导、粗糙海面等对海上电波的影响，模拟了雷达的有效覆盖范围，结果表明提出的模型能有效地计算复杂海洋环境的电波传播特性. 本文研究对未来海上电子战的发展具有重要的参考价值.