基于GNSS的武汉区域电离层TEC建模

吴伟铨 周晨 禹智斌 左平兵 赵家奇 赵正予

（1. 武汉大学电子信息学院空间物理系，武汉 430072；2. 哈尔滨工业大学空间科学与应用技术研究院，深圳 518055）

引 言

电离层天顶方向总电子含量(vertical total electron content, VTEC)是卫星导航系统的重要产品. 近年来不少优秀的学者利用经典的电离层模型，对VTEC进行了建模研究. Lanyi等[1]提出利用2阶或3阶多项式模型计算单站VTEC；Schaer等[2]利用球谐级数模型进行全球电离层建模；Yuan等[3-4]提出广义三角级数函数模型，该模型在小区域VTEC 建模中有很好的效果. 在各种电离层模型被提出之后，又有不少专家学者对这些模型进行了比较分析. 文献[5]对多项式模型、三角级数模型和低阶球谐级数模型之间的一致性和参数设置局限性进行了分析，指出了它们的优缺点. 文献[6]根据应用环境对电离层模型进行了分类，并提出了模型的一些问题和改进措施. 文献[7]指出了多项式模型和三角级数模型不适用于大区域的电离层建模. 文献[8-9]表明在模型参数选取适当的情况下，球谐级数模型适用于各种大小区域的电离层建模. 文献[10]基于球谐级数模型对山东区域进行电离层建模，并采用单频精密单点定位验证了该区域电离层模型的有效性. 电离层在不同高度上的电子密度会有很大差异, 文献[11]提出了一种三层的电离层模型，可以反映不同高度区域的VTEC情况. 在电离层建模中，通常要采用一定的估计策略来对模型系数进行估计. 常采用的是分段常数(piece-wise constant, PWC)估计策略和分段线性(piece-wise linear, PWL)估计策略. 文献[12]指出，只有在低纬度地区的电离层模型改正精度才会对估计策略比较敏感，而这种影响是随纬度升高而减小的. 文献[13]在总结全球导航卫星系统(Global Navigation Satellite System, GNSS)电离层延迟修正成果的基础上，从建模及误差分析等方面介绍了我国在这一领域的研究进展. 但是，上述文献都没有对电离层建模方法和估计策略进行综合对比分析，也没有研究地磁活动对电离层建模的影响. 因此，本文在上述研究的基础上，对武汉地区进行电离层建模，目的是比较不同建模方法和估计策略在该区域中的适用性，以及探究地磁活动和电离层建模的相关性.

国际GNSS服务(International GNSS Service,IGS)的电离层联合分析中心(Ionosphere Associate Analysis Centers, IAACs)可以提供高精度的电离层产品，主要包括欧洲轨道确定中心(Center for Orbit Determination in Europe, CODE)[8]、美国喷气推进实验室(Jet Propulsion Laboratory, JPL)[14]、欧洲太空局(European Space Agency/European Space Operations Center, ESA/ESOC)[15]、西班牙加泰罗尼亚理工大学(Universitat Politècnica de Catalunya, UPC)[16]、加拿大自然资源部门(Natural Resources Canada, NRCan)、中国科学院测量与地球物理研究所和光电研究院(Chinese Academy of Science, CAS)[17]及武汉大学卫星导航与定位技术研究中心(Wuhan University, WHU)[18].本文选择CODE提供的电离层产品作为参考源，其采用15阶球谐级数进行全球的电离层建模，能提供时间分辨率为1 h、空间分辨率为2.5°×5°的全球电离层格网地图(global ionospheric map, GIM)[19]. 选取以武汉为中心的十七个连续运行参考站(continuous operation reference system, CORS)在不同地磁活动情况下的数据进行试验，并与CODE公布的GIM作对比，对于分析建立武汉地区的电离层模型、削弱电离层延迟误差具有重要意义[10].

传统的二维电离层模型是区域电离层建模的经典手段，但是，它们只能根据经度和纬度拟合区域内的VTEC，却不能反映高度上的电子密度变化情况.而通过三层电离层模型可以从经度、纬度、高度三个维度上对电离层进行建模，并且可以有效提高电离层地图的拟合精度[11]. 此外，多层电离层模型对空间目标监视和低轨卫星航天测控具有重要应用价值.本文通过研究三种二维电离层模型和估计策略对VTEC计算精度的影响，探索适用于武汉区域的电离层模型、模型参数和估计策略，以及分析模型精度和地磁活动的相关性. 在此研究的基础上，进一步通过三层电离层模型，来分析不同高度区域的VTEC情况.

1 电离层模型

二维电离层模型包括多项式模型、三角级数模型、球谐级数模型、样条函数模型、广义三角级数模型. 下面主要介绍多项式模型和球谐级数模型，以及在二维电离层模型基础上提出的三层电离层模型.

1.1 多项式模型

多项式模型[1]将VTEC看作如下表达式：

式中：Tv(φ,S)是电离层穿刺点(ionosphere piece point,IPP)处的VTEC；m和n是 模型阶数；Eij是模型系数；φ是地理纬度； φ0是IPP覆盖中心的地理纬度；S是太阳时角；S0是IPP覆盖中心的太阳时角.

太阳时角S具有如下形式：

式中：θ是地理经度，单位是(°)；t是UTC时间，单位是h.

通常求解一个多项式模型用2～3 h，所以要每2～3 h计算一组模型系数.

1.2 球谐级数模型

球谐级数模型[2]的表达式如下：

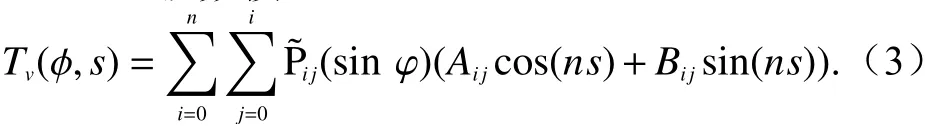
式中：n是模型阶数；(sinφ) 是i度j阶的缔和勒让德函数；φ是IPP的纬度；s是IPP的经度；Aij和Bij是模型系数.

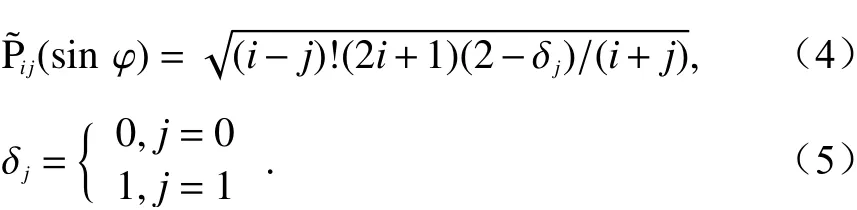
求解球谐级数模型也是使用2～3 h. 区域电离建模时，可以采用低阶的球谐级数模型.

1.3 三层电离层模型

三层电离层模型[11]把总电子含量(total electron content, TEC)看成与经度θ、纬度φ和高度h都相关的函数，其表达式如下：

式中：T是发送机到接收机路径上的TEC；Rtra和Rrec分别是发送机和接收机的位置；Ne(θ,φ,h)是电子密度函数. 即TEC是电子密度沿发送机和接收机路径的积分. 电子密度函数可看成水平基函数和垂直基函数的线性组合，表达式如下：

式中：cij是 参数；Hi是水平方向的电子密度基函数，可沿用在二维电离层模型中使用的函数；Vj是垂直方向的电子密度基函数，可采用国际参考电离层(international reference ionosphere, IRI)模型[20]输出的电子密度作为该函数；NH和NV是两个基函数的阶数.

三层电离层模型把VTEC看作如下表达式：

式中：Tv(φ,S,h1,h2)代 表纬度φ、 太阳时角S、高度h1到h2之 间的VTEC；Tv(φ,S,0,∞)是二维电离层模型计算的结果；cj是参数. 即通过垂直方向电子密度函数的积分可以得到与高度、纬度、经度都相关的VTEC.

2 武汉地区电离层建模

本文对武汉周边17个CORS 2016-01-01—05的数据进行建模，如图1所示. 图2是2015-12-31—2016-01-07的地磁活动指数(Dst和Kp). 可以看到，01-01处在磁暴恢复相期，而01-05处在地磁平静时期，选取这两天数据有利于研究不同地磁活动水平对区域电离层建模的影响.

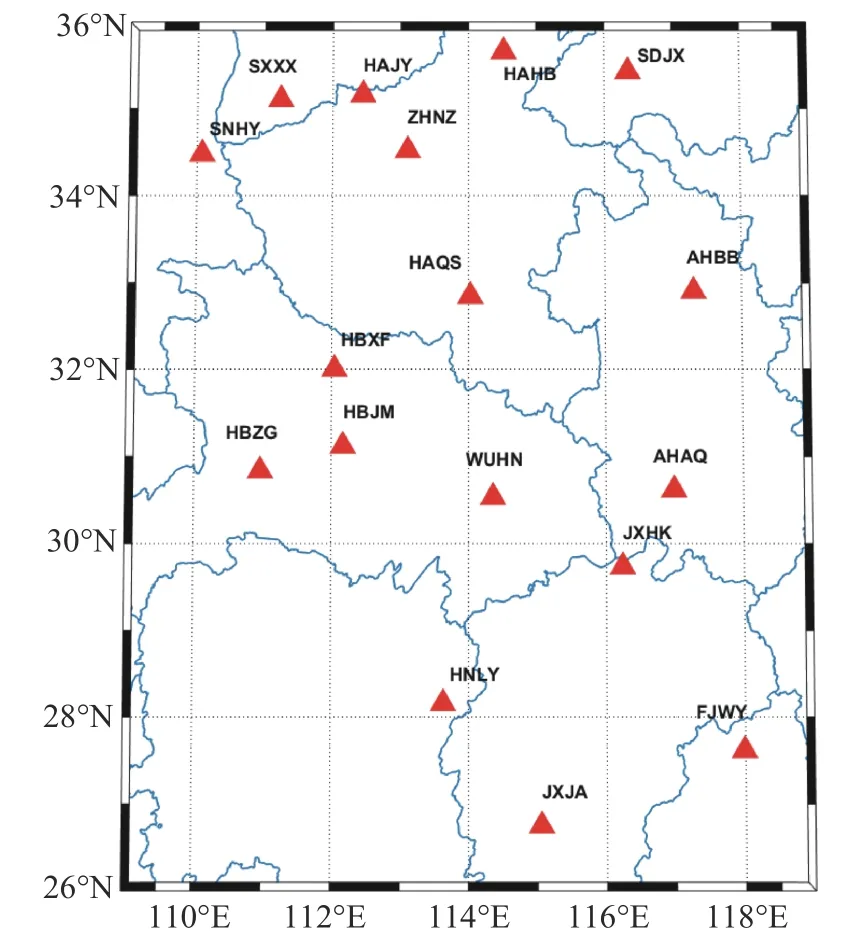
图1 武汉周边17个CORS分布图Fig. 1 Distribution map of 17 continuously operating reference stations around Wuhan

图2 2015-12-31—2016-01-07 Dst指数和Kp指数Fig. 2 Dst index and Kp index from Dec. 31st,2015 to Jan. 7th, 2016

2.1 建模方法

本文基于GNSS观测数据，使用载波相位平滑伪距法[14]提高伪距观测精度，卫星截止仰角设置为15°，投影函数采用标准投影函数，时间采样率为30 s，电离层薄层高度设置为450 km.

本文利用参考文献[1]中提出的2阶多项式模型、文献[5]中使用的4阶球谐级数模型，以及文献[21]中使用的4×3阶多项式模型这三种模型进行区域VTEC建模. 估计策略分别采用PWC估计策略和PWL估计策略[12]. PWC假定VTEC模型系数在适用时间内不变；PWL假定模型系数在这段时间线性变化，通常需要两组系数，分别代表该时间段开始和结束时的模型系数，则任意时刻的模型系数都能由这两组系数线性表示. 将VTEC模型系数和硬件延迟偏差(differential code biases, DCB)联合建立法方程[22]，采用最小二乘法，每2 h计算一组系数. 得到联合DCB后，通过假设所有卫星的DCB之和为零来分离接收机和卫星DCB. 按照0.1°的间隔划分网格点，求得模型系数后再反代入网格点，计算出各网格点处VTEC.

2.2 结果和分析

对2016-01-01的数据进行建模，采用PWC估计策略时，4×3阶多项式模型、2阶多项式模型、4阶球谐级数模型的VTEC建模结果如图3所示.

图3 2016-01-01三种模型采用PWC估计策略的VTEC建模结果Fig. 3 Modeling diagram of three models and piece-wise constant strategy on Jan. 1st, 2016

对2016-01-05的数据进行建模，采用PWC估计策略时，4×3阶多项式模型、2阶多项式模型、4阶球谐级数模型的VTEC建模结果如图4所示.

图4 2016-01-05三种模型采用PWC估计策略的VTEC建模结果Fig. 4 Modeling diagram of three models and piece-wise constant strategy on Jan. 5th, 2016

从图3～4的二维电离层模型结果可以看出：在0:00—6:00UT时，电离层电子浓度逐渐增大，并在6:00UT时达到峰值，而在16:00—24:00UT电子浓度都偏小；低纬度地区的电子浓度比高纬度地区高；发生磁暴时，电离层电子浓度显著增大，说明地磁活动会影响电离层的电子浓度.

鉴于CODE在硬件延迟及电离层解算方面的优越性，采用CODE公布的GIM作为外部对比源. CODE提供的该区域2016-01-01和01-05的VTEC结果如图5所示.

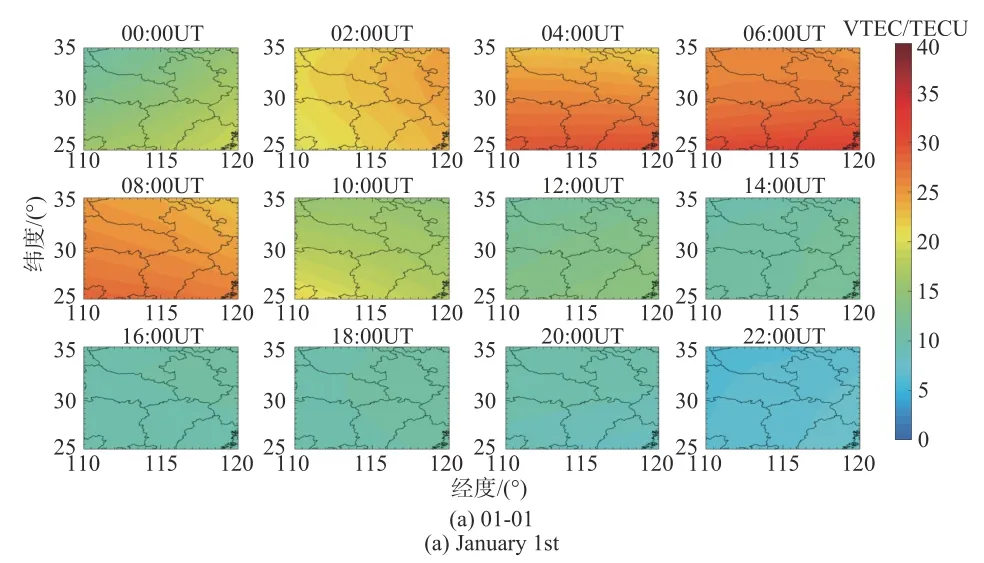
图5 2016-01-01和01-05 CODE公布的VTEC建模图Fig. 5 Modeling diagram published by CODE on Jan. 1st and Jan. 5th, 2016

通过三种模型的VTEC建模图和CODE公布的建模图进行对比可以发现，三种模型都能达到较好的拟合效果. 为了进一步分析这些模型在地磁平静时期和地磁扰动时期的建模精度变化，对武汉单站VTEC在PWC估计策略下的计算结果和CODE公布值进行了比较，结果如图6所示.

图6 2016-01-01和01-05武汉单站VTEC建模结果和CODE公布结果对比Fig. 6 Comparison of VTEC modeling results and code results of Wuhan single station on Jan. 1st and Jan. 5th, 2016

从图6可以看出，三种模型的建模结果几乎重叠在一起，且和CODE公布的VTEC变化趋势基本一致，但VTEC大小依然存在一定的误差. 原因是CODE进行的是全球电离层拟合，在中国区域用的站不到十个，在小区域范围内拟合精度不够.

鉴于此原因，本文将VTEC通过电离层投影函数转化成斜向总电子含量(slant total electron content,STEC)，与实测值比较计算30天的残差值均方根(root mean square, RMS)，以此来分析模型和估计策略的精度. 其中残差值的表达式如下：

式中：R是残差值；TS是STEC的观测值；fm是电离层投影函数，定义为STEC和VTEC的比；TV是VTEC；D是DCB.

统计2016-01-01—30的STEC残差值RMS，在PWL和PWC估计策略下的结果如图7所示.

图7 两种估计策略下的RMS分布Fig. 7 RMS distribution with two estimation strategies

从图7的残差RMS结果可以看出：无论采用哪种估计策略，效果最好的是4阶球谐级数模型，其次是4×3阶多项式模型，而2阶多项式模型的效果最差，这与其模型参数较少有关；三种模型在PWL估计策略下的效果要优于PWC估计策略，说明PWL估计策略更适用于区域的VTEC建模. 当使用PWL估计策略和4阶球谐级数模型时，RMS集中在0～1.5 TECU，区域VTEC建模达到较高的精度.

对比01-01和01-05的残差，发现01-05三种模型的RMS都比01-01对应的RMS要小. 另外，从图6可以看出，同一时刻，模型的计算结果会比CODE公布值小，除了在01-01T6:00UT，此时VTEC也恰好达到峰值. 从以上的分析可以推断出，地磁扰动会对VTEC计算结果产生干扰. 一方面，地磁活动强的时候GNSS观测误差会增大；另一方面，VTEC模型的计算精度也会降低.

谷子生育期为80～140 d，适合小麦、大麦等收后复种。笔者在内蒙古农牧业科学院试验地曾进行饲用谷子不同生长时期全株营养物质测定试验，结果表明：初花期预干全株的蛋白质含量要明显高于成熟期的蛋白质含量，而初花期预干全株的纤维含量要明显低于成熟期纤维含量，初花期预干全株的干物质量与成熟期相当，所以饲用谷子在初花期就可以进行收获，大大缩短了生长周期，是短日期作物收获后复种的优良作物之一。

以上都是基于经度和纬度的二维电离层建模.然而，二维电离层模型不能反映VTEC与高度之间的关系. 为了进一步研究底部电离层、峰高电离层和顶部电离层的VTEC情况，本文在上述研究的基础上利用三层电离层模型对武汉地区进行建模. 参考文献[11]中对电离层高度的分层方法，将电离层分为三个区域：90～350 km，350～600 km，600～1 500 km. 利用IRI模型计算出每个IPP三个高度区域的VTEC比例，再代入4阶球谐级数模型在PWC估计策略下的计算结果中，构建出三层电离层模型.2016-01-01和01-05的建模结果如图8所示.

图8 2016-01-01和01-05三层电离层模型建模Fig. 8 Modeling diagram of three layer ionosphere model on Jan. 5th, 2016

从图8可以看出：90～350 km高度区间的电离层TEC最大，其次是350～600 km，而在600 km以上，TEC会变得很稀少. 在得出该结果后，本文进一步研究三层电离层VTEC随时间的变化规律. 利用2015-12-31—2016-01-06七天的数据，对武汉上空的VTEC进行了计算，得出三个高度区间以及总的VTEC结果如图9所示.

从图9可以看出：在每天VTEC达到峰值时刻前后，底部电离层的VTEC要明显大于峰高电离层和顶部电离层的VTEC. 当VTEC在谷值时，底部VTEC和峰高VTEC较为接近. 同时，不同高度的VTEC对地磁活动变化的响应也有明显区别，底部TEC和峰高TEC受地磁活动的影响较大.

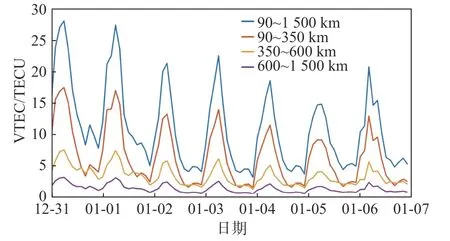
图9 2015-12-31—2016-01-06武汉上空三层电离层VTEC结果Fig. 9 VTEC results of three layers over Wuhan from Dec.31st, 2015 to Jan. 6th, 2016

3 结 论

本文针对区域电离层建模的三种模型和两种估计策略，分别选取地磁平静和地磁扰动的两天数据进行计算，并以CODE公布的GIM和STEC实测值作为对比源进行分析，得出一些结论.

1)在区域VTEC建模中，三种二维电离层模型的建模结果和CODE公布的GIM基本一致，达到较好的拟合精度.

2)地磁扰动会对模型的拟合结果产生干扰，降低模型的拟合精度.

4)当使用PWC估计策略时，所有模型的拟合效果都会变差. 因此，在该区域VTEC建模中建议使用PWL估计策略.

5)从三层电离层模型结果可以看出，电离层的电子含量集中在90～600 km高度区间，不同高度的VTEC对地磁活动变化的响应有很大区别.

文中的试验是基于武汉周边地区两天的数据来进行的，没有考虑不同的地区和更长时间的情况. 而且，模型的精度受实际应用场景和观测数据密集程度等多种因素的影响，为了达到详细的分析对比，需要进行更加完善的试验设计.