基于KNN-TSVR算法的MIMO-OFDM系统信道估计

李 朔， 雷为民， 张 伟

(1. 东北大学 计算机科学与工程学院， 辽宁 沈阳 110169； 2. 辽宁科技大学 电子与信息工程学院, 辽宁 鞍山 114051)

新兴的5G通信系统、家庭音频/视频网络以及无线局域网等系统的发展对高速无线通信技术提出了较高的要求.在非视距情形下高速数据传输速率仍然因为信道衰落和噪声污染等原因而不能满足需求；另外，宽带传输系统也存在通信距离延长的问题.多输入多输出(multiple input multiple out，MIMO)无线通信技术由于其阵列增益、分集增益、空间复用增益和抗干扰性能的提高，部分地解决了上述问题.正交频分复用(orthogonal frequency division multiplexing，OFDM)将串行的数据流转换为多路并行的低速数据流，在多个载波上同时进行传输，扩大了符号间的时间间隔，这样可以降低传输中的多径效应对传输的不利影响.在接收端采用相干解调方法可以降低传输过程中对于信噪比(SNR)的要求，使得每个子信道上的信号带宽小于信道的相关带宽，这样每个子信道可以看成是平坦衰落的，从而消除码间串扰.正是由于MIMO和OFDM技术的这些优点，MIMO-OFDM被4G和5G无线通信系统所采用.

有许多方法用来估计选择性信道，其中包括最小二乘(LS)法[1]、线性最小均方误差(LMMSE)法及其改进算法[2-4].文献[5]提出了基于双选择性信道基扩展模型(BEM)的OFDM系统的信道估计算法，文献[6]为OFDM设计了自适应加权估计器；这些算法从不同的技术路线提升了信道估计性能，但这些方法将通信信道模型假定为线性的[7-9].OFDM的自适应加权均衡估计器[10]在选择性多径衰落信道的情况下，由于元件饱和、光纤色散等原因，信道响应呈现出复杂的非线性，如果采用线性方法，可能会降低估计精度；因此，有必要对信道进行非线性分析.文献[11]中提出了一种基于非线性Kalman滤波器的OFDM系统高速信道估计算法,文献[12]提出了一种基于深度学习的信道估计方法.

目前关于将孪生支持向量回归(twin support vector regression，TSVR)算法[13]应用于OFDM通信系统信道估计的研究，主要集中于利用经典的TSVR算法改进LTE(long term evolution)系统的信道估计[14]；这些算法虽然在估计性能上有所提高，但同时存在计算量大、收敛速度较慢等问题[15].本文结合OFDM系统和MIMO-OFDM系统的特征[16-17]，重点从如何在控制和降低计算代价前提下，加快非线性控制模型的收敛速度并提升估计性能等方面展开研究，设计并验证评价了新的估计算法，即K近邻加权孪生支持向量回归(KNN-TSVR)算法.

1 MIMO-OFDM系统模型

MIMO-OFDM系统模型如图1所示，假定系统有MT个发射天线和MR个接收天线.

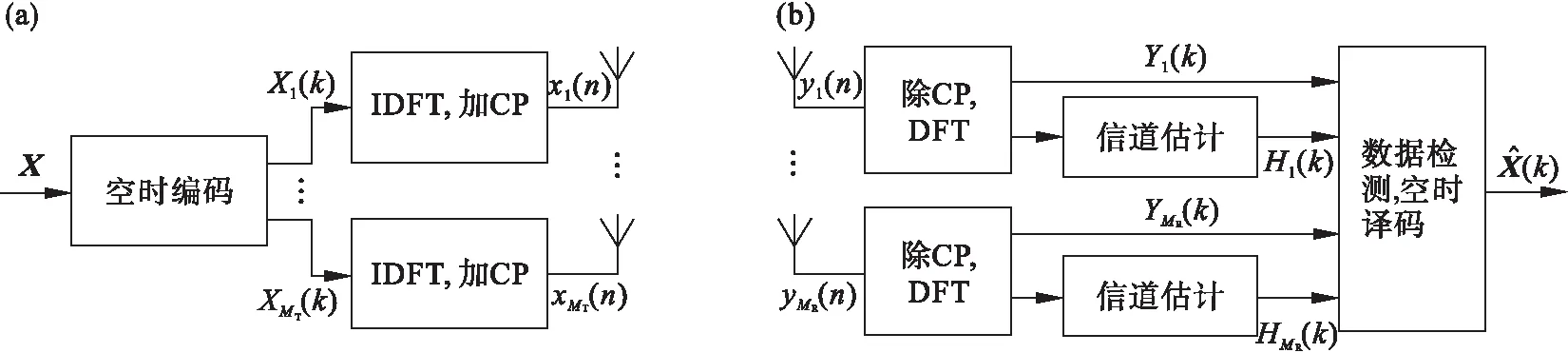
图1 MIMO-OFDM系统基带等效模型

Xi(k)是待发送信号X经过空时编码器输出的待发送信号序列，被分成N个块, 由QPSK星座映射得到；Xi(k)=Aicosθicos(ω0k)-Aisinθisin(ω0k)(k=0, 1,…,N-1，i∈MT).其中Ai和θi分别表示第i个接收天线上星座图中映射点的幅度和相位，ω0表示载波基频频率.使用离散傅立叶逆变换(IDFT)对Xi(k)进行频率调制，为了避免码间串扰，将长度为LCP的循环前缀(cyclic prefix，CP)插入到每个块的头部，再将输出序列解析成n个符号的块(n=1,…,N-1)，然后采用IFFT变换成时域序列，得到发射天线的待发送时域信号xi(n)：

(1)

xi(n)通过无线信道到达接收天线，在接收端去除CP后， 接收到的时域信号为y(n)：

(2)

式中：v(n)=[v1(n),v2(n),…,vMR(n)]T是加性高斯白噪声(AWGN)，vi(n)(i=1,2,…,MR)的期望值和方差分别为0和σ2，且v(n)各元素间相互独立；hi(n,l)=[hi,1(n),hi,2(n),…,hi,MR(n)]T是第i个发射天线到各接收天线的信道冲激响应向量.令Y(k)为去掉CP后在第k个子载波处的频率响应向量：

(3)

将式(2)代入式(3)可得

(4)

2 空时编码传输

在发射端，数据传输可采用Alamouti空时编码方案来获得分集增益.最简单的MIMO-OFDM系统有两个发射天线和一个接收天线，即2I1O-OFDM，该系统的空时编码可以用下面的矩阵表示：

(5)

式中：(·)*是取复共轭；X表示待发送信号；下标1和2分别表示天线1和天线2；下标o和e分别表示待发送信号的奇数和偶数序列.如果信道响应在连续的两个符号周期内保持不变，则接收天线接收到的频域信号为

(6)

式中：Xo(k),Yo(k)和Vo(k)(Xe(k)，Ye(k)和Ve(k))分别表示奇序列(偶序列)的第k个子载波处的发射信号、接收信号和噪声；H1(k)和H2(k)分别对应于第1个和第2个发射与接收天线间第k个子载波处的信道响应.

3 MIMO-OFDM系统信道估计

经典的信道估计是基于线性假设的，在对非线性的无线通信信道进行信道估计时会产生估计误差.本文利用TSVR对非线性系统的回归特性，采用改进的加权TSVR估计算法(即KNN-TSVR算法)来估计MIMO-OFDM信道的频率响应.

3.1 导频子载波信道估计

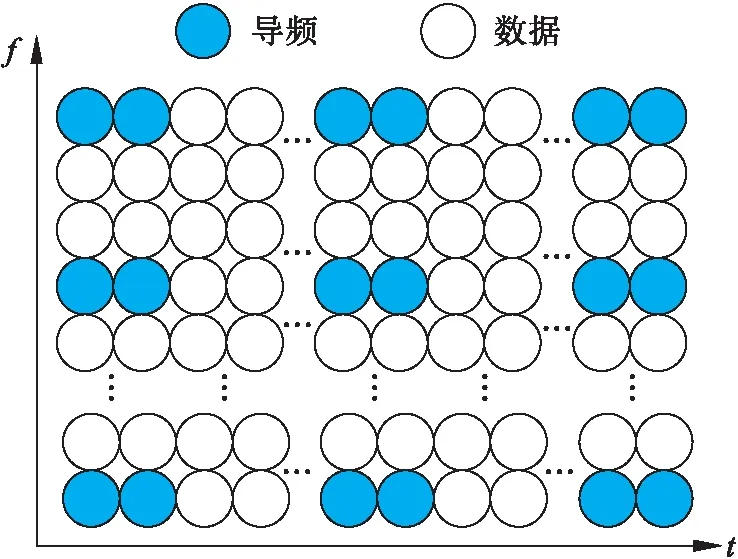
图2 导频插入方案

由式(6)可以得到信道频率响应估计值：

(7)

(8)

3.2 信道估计算法

给定一个训练集S={(τ1,r1),(τ2，r2),…,(τm,rm)}；τk∈R2为输入在时域和频域的位置，rk∈R为导频点冲激响应的实部或虚部，作为训练输出；m为训练样本数目.将所有训练输出堆叠构成输出向量R=[r1,r2,…,rm]T，所有训练输入堆叠构成输入矩阵T=[τ1,τ2,…,τm]T.

采用KNN-TSVR来估计MIMO-OFDM系统的信道响应.与经典的TSVR相似，回归函数由下界f1(τ)和上界f2(τ)组成，最后的回归函数可取上下界的平均值：

(9)

为了回归非线性关系,可以采用核函数映射方法将训练样本映射到更高维空间：回归函数的上下界分别为f1(τ)=K(τ,TT)g1+δ1和f2(τ)=K(τ,TT)g2+δ2，其中K是核函数，g1，g2∈Rm,δ1，δ2∈R是待估计参数.f1(τ)和f2(τ)的平均值是最终的回归结果，与线性回归方法(9)的表达式相同.优化问题可以表示为

s.t.R-(K(T,TT)g1+eδ1)≥-ε1e-η1，

ε1≥0，η1≥0.

(10)

s.t. (K(T,TT)g2+eδ2)-R≥-ε2e-η2，

ε2≥0，η2≥0.

(11)

式中：v1,v2,c1,c2,c3,c4>0为预选参数；ε1,ε2为不敏感常数；η1,η2为反映训练样本是否位于ε管内的松弛向量；d=[d1,d2,…,dm]T,D=diag(d)分别为权值向量和权值矩阵，用KNN算法计算.

目标函数(10)和(11)是基于结构最小化原则提出的，该原则有助于弱化过拟合问题，提高回归性能.用拉格朗日乘子将它们映射到对偶空间中再优化问题进行求解.这样，式(10)可以转化为

(12)

式中：α=[α1,…,αm]T；β=[β1,…,βm]T；γ>0是拉格朗日乘子.利用Karush-Kuhn Tucker(KKT)条件，可以得到对偶问题为

(13)

其中Λ=[K(T,TT)e].

通过计算对偶QPP问题，即式(13)，可以得到

(14)

类似地，式(11)的解为

(15)

式中，λ为式(11)转化为对偶空间QPP问题的拉格朗日乘子.

这样，可以利用导频所在位置的信道响应作为训练数据，通过求解对偶优化问题，分别获得各个接收天线对应的无线信道中所有时频位置上的信道响应.

4 仿真实验

通过仿真实验对本文提出的基于KNN-TSVR的MIMO-OFDM系统的信道频率响应估计算法进行性能分析.同时，对线性插值算法和经典TSVR算法也进行性能仿真，以便与本文算法进行性能比较.

在接收端，MR个接收天线中任意一个天线都需要独立估计MR个信道响应，因此不失一般性地选择2个发射天线，1个接收天线，即考虑一个具有双衰落信道的2I1O-OFDM系统作为测试实例.传输路径的数目L=5，各信道抽头被假定为独立且分布相同.信道响应在时间上是相关的，可以表示为

E(h(n1,l1)h*(n2,l2))=

σ2J0(2πfmaxTs(n1-n2))δ(l1-l2) .

(16)

式中：E(·)表示取期望值；(·)*表示取共轭；ni和li(i=1，2)分别是时间和信道路径标记；J0是第一类零阶贝塞尔函数；Ts和σ2是采样间隔和信道冲激响应的方差.系统参数：调制方式为16-QAM，载波频率fc=2.15 GHz，一个码元内子载波数N=128，循环前缀长度LCP=5，采样间隔Ts=72 μs，通信终端与基站间的相对移动速度分别为120和350 km/h.仿真时在时域和频域中同时插入导频.将高斯函数作为非线性映射核：

(17)

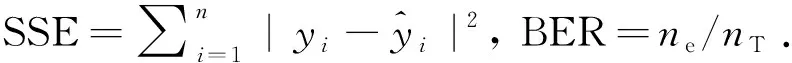
图3给出了KNN-TSVR对非线性信道的回归情况，其中SNR=10dB，路径数目L=5，移动速度v=350 km/h，图例*是作为训练样本的有噪声信道响应.由图3可见，本文算法的预测曲线和无噪声条件下的已知函数曲线接近，拟合曲线平滑，拟合效果较好，KNN预处理有效.

图3 KNN-TSVR对信道频率响应的回归

图4和图5分别为Δt=Δf=4，Δt=Δf=8条件下不同移动速度时信噪比对误码率的影响，其中，Δt为导频插入的时域间隔，Δf为导频插入的频域间隔.为了将本文算法与现有的其他典型算法进行性能比较，图中同时还给出了线性插值法、基于经典TSVR的估计方法，以及已知信道参数的BER曲线.

图4 不同移动速度时信噪比对误码率的影响(Δt=Δf=4)

图5 不同移动速度时信噪比对误码率的影响(Δt=Δf=8)

由图4和图5可以看出：随着信噪比的增加，本文方法的BER有较显著的下降.当信噪比小于10 dB时，由于加性噪声是主要的干扰因素，本文算法的BER的下降并不显著；移动速度的加快会使BER有所上升，这是因为移动速度越快，信道间干扰就越大，导致BER上升.本文方法与基于经典TSVR算法的误码率曲线趋势相似，性能优于线性插值方法，说明SVR具有非线性关系的回归优势.对比图4和图5可以看出，时间间隔和频率间隔增加，使得插值间隔增大，导致回归性能下降.信道频率响应的SSE如表1所示，这些结果是50次蒙特卡洛运行得出的平均值.表1的结果也从SSE的角度给出了相同的结论，进一步验证了本文算法的有效性.

表1 估计方法的SSE

5 结 语

训练样本数的增加使支持向量机的计算复杂度显著增加，因此，本文在保证估计精度的前提下降低计算复杂度，给出了一种基于KNN-TSVR的MIMO-OFDM信道频率响应估计器：该方法在发送端，在数据序列中插入导频信号，经过编码处理通过天线发送出去；在接收端，经过OFDM解调和空时解码，利用基于KNN-TSVR的估计器进行插值.采用KNN算法计算某个样本周围的样本数量来判别该样本自身的重要性，并由此得到用于改进TSVR的权值，从而提高回归性能.本文方法适用于基于时间序列样本的回归，将其用于MIMO-OFDM系统信道参数的辨识可提高信道估计的性能.