基于模糊数学的STS管幕结构的连接参数优化
2022-03-08曹文欣贾鹏蛟
曹文欣, 赵 文, 路 博, 贾鹏蛟
(1. 东北大学 资源与土木工程学院, 辽宁 沈阳 110819; 2. 苏州大学 轨道交通学院, 江苏 苏州 215131)
在“交通强国”战略的驱动下,我国轨道交通得到快速发展.截至2020年,我国已有44座城市开通地铁,总里程数超过6 500 km.而地铁路网的不断完善,难免会出现新老地铁线路的交叉和地铁换乘站建设等施工难题.以洞桩法为代表的传统浅埋暗挖法在地质情况较为复杂的区段施工时难以满足施工安全的要求,而管幕法以安全性高、能有效控制地表沉降等优点而逐渐被应用到城市地铁工程的建设当中[1-2].
管幕工法是利用顶管机将钢管顶入土中,再将钢管横向连接形成整体,然后在管幕结构支护下进行地下空间施工的一种方法.1962年日本在东海道新干线第一热海隧道工程施工中使用了管幕工法,在1971—1980年间日本采用管幕工法施工的工程就有6项,管幕工法在日本得到了较多的应用[3-4],随后管幕工法在日本、新加坡、美国得到快速发展和广泛应用[5-10],20世纪80年代中期中国香港首次应用管幕工法,进入21世纪后,管幕工法逐渐被运用于北京、上海和沈阳等城市的地铁车站及地下通道工程中.然而传统管幕结构的管间通过锁口连接,使得钢管连接部位较为薄弱,需要边开挖边支撑以确保安全,不利于我国轨道交通的快速发展[11].针对上述问题,赵文及其研究团队提出了STS(steel tube slab)新型管幕支护体系,它在相邻钢管间采用高强螺栓并焊接下翼缘板以提高支护体系的抗弯承载力和刚度,弥补了传统管幕结构的不足.
Xiao等[12]在考虑管土相互作用和混凝土弹性模量的基础上分析管幕的整体受力模式,研究了管幕在施工过程中的力学机制;赵文等[13]通过室内试验对STS管幕构件的横向抗弯性能进行研究,并得出了翼缘板焊接、钢管间距、混凝土强度等级和翼缘板厚度等参数的变化对STS管幕构件抗弯性能的影响规律;关永平等[14]基于6榀STS管幕简支梁的对称集中荷载抗弯试验,分析了混凝土强度、钢管间距及管间横向连接形式对承载力的影响规律,并通过数值计算给出了翼缘板厚度及钢管壁厚比的合理取值范围;贾鹏蛟等[15]基于室内试验,利用数值模拟的方法深入研究钢管厚度、螺栓直径、配筋率、翼缘板间距等连接参数对STS管幕构件横向力学性能的影响,其中翼缘板间距的调整对试件的极限承载力和横向刚度具有显著的影响;Jia等[16-18]结合沈阳地铁十号线东北大马路站工程监测数据,提出STS管幕结构作为永久性支撑系统能够有效控制和减少地表沉降,通过室内试验研究STS管幕结构的破坏过程和裂纹发展规律,并得到了STS管幕结构的荷载-位移曲线,结果表明下翼缘板焊接能够显著提高STS管幕结构的抗弯能力.此外,一些学者在管幕结构的连接形式上开展了进一步的研究.Zhang等[19]提出了槽钢连接的管幕结构设计方法,并通过设计试验和数值模拟,得到了槽钢连接的管幕结构破坏模式,而后分析了该结构的横向抗弯承载力和横向抗弯刚度;赵文等[20]提出了咬合型管幕结构,并分析了咬合程度、钢管壁厚及上侧焊接长度等参数对咬合型管幕结构的横向抗弯刚度性能的影响规律.综上所述,目前对STS管幕结构的横向抗弯承载力、横向刚度以及影响参数的研究较为细致,而对其纵向受力的研究较少,使得设计工作偏向于利用管幕结构的横向受力特性来评估整体结构的受力,从而导致结构受力不合理和材料的浪费.
基于此,本文通过ABAQUS软件建立三维有限元模型,并基于STS管幕结构纵向抗弯性能试验验证数值模型的有效性和正确性,对不同参数组合下的STS管幕构件纵向抗弯性能进行系统分析,并结合多指标正交试验,引入经济性指标分析不同参数组合的经济性;随后,结合模糊数学理论对结构参数进行优化,使得到的最优连接参数能够同时兼顾安全性和经济性,研究结果能够为STS管幕结构的设计和施工提供指导.
1 STS管幕结构简介
STS管幕结构是一种用于修建地铁车站或下穿既有道路、地下管线等现有结构物的新型地下支护体系.它是由若干个相互平行、共同受力的钢管组成,钢管之间通过高强螺栓和焊接翼缘板连接,并在管内和管间浇筑混凝土使其成为一个共同受力的组合结构,STS管幕结构见图1.

图1 STS管幕结构示意图
1.1 施工步序
STS管幕结构施工步序[21]:①在设计位置顶进钢管;②钢管顶进过程中进行实时纠偏并清理管间土体;③在相邻钢管间安装横向连接螺栓;④在钢管端部焊接钢板后浇筑管内和管间混凝土;⑤开挖管幕结构下方土体,而后对翼缘板进行焊接,完成主体结构施工.STS管幕构件加工见图2.
1.2 结构特点
STS管幕结构相较于传统管幕结构主要有以下优势:①钢管间由高强螺栓和焊接翼缘板连接,且在管内和管间浇筑混凝土,大大提高了管幕结构的抗弯性能;②取消了传统管幕结构架设临时支撑的复杂施工步序,同时极大地提升了地下工程施工的安全性.此外,STS管幕结构结合洞桩法施工,相比于传统管幕结构更适用于超浅埋大跨度地铁车站建设.

图2 STS管幕构件加工图
2 STS管幕构件有限元模型的建立
2.1 单元选取
有限元模型中钢管与上、下翼缘板均采用了四节点减缩积分格式的壳单元(S4R);管内和管间混凝土和上、下钢垫块均采用了八节点减缩积分格式的实体单元(C3D8R);横向连接螺栓则采用两节点线性积分格式的三维桁架单元(T3D2),主要部件网格图见图3.
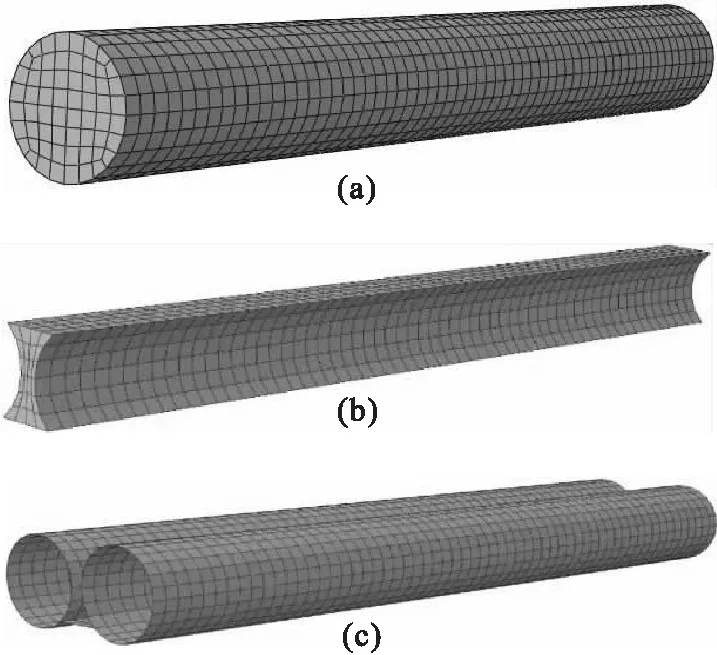
图3 有限元模型网格图
2.2 材料本构模型
建模过程中,钢垫块取为弹性模型;横向连接螺栓和上、下翼缘板均采用理想弹塑性模型[22];管间混凝土的本构模型采用《混凝土结构设计规范》(GB 50010—2010)中的应力-应变关系曲线模拟;钢管内部混凝土的本构模型采用由韩林海[23]提出的钢管混凝土单轴应力-应变关系曲线.
2.3 接触模拟
钢管与管内混凝土及钢管、翼缘板与管间混凝土之间的相互作用采用表面与表面接触来模拟.混凝土与钢管、翼缘板接触面之间的作用分为法向和切向,本文模型中采用“罚函数”定义切向作用,摩擦系数取为0.2;法向作用为“硬”接触,即两个接触面脱离后,两部件之间的相互作用将不再存在;螺栓使用Embedded region命令嵌固在混凝土内部;垫块与钢管接触面采用Tie命令约束.
2.4 边界条件及加载方式
为达到较好的模拟效果,有限元模型的边界条件及加载方式与试验保持一致,即边界条件模拟简支梁的形式;模型的边界条件施加在垫块底面,垫块上各耦合一参考点,集中荷载便施加于其上;数值模拟中加载方式采用单调静力加载.构件的边界条件和加载方式见图4.

图4 构件边界条件和加载方式
3 试验验证
3.1 试验概况
贾鹏蛟[11]通过STS管幕结构纵向抗弯性能试验研究了不同参数下STS管幕构件纵向抗弯性能的变化规律.主要变化参数为相邻钢管连接方式、相邻钢管中心间距、焊接上翼缘板及下翼缘板厚度等,试验中采用了对称集中静力加载直至试件破坏的加载方式.
3.2 有限元模型
本文依据STS管幕结构纵向抗弯性能试验中LCB-2和LCB-6构件的参数建立有限元分析模型,其具体的结构连接参数见表1.

表1 标准构件连接参数表
3.3 数值模拟与试验结果对比分析
构件LCB-2和LCB-6的荷载-位移曲线见图5.由表2对比结果分析表明计算值与试验值吻合良好.

图5 室内试验结果与数值计算结果对比

表2 数值计算与试验结果对比
4 STS管幕结构参数分析
本节主要通过正交试验研究钢管壁厚、钢管直径、螺栓直径、钢管间距和翼缘板厚度对STS管幕构件的纵向抗弯性能及经济性指标的影响.
4.1 正交试验设计及评价指标计算
正交试验的3个评价指标、5因素及5水平如下:
1) 评价指标:构件达到屈服荷载时的跨中位移y1,构件纵向抗弯承载力y2,每延米构件材料平均价格y3.
2) 因素:钢管壁厚x1,钢管直径x2,螺栓直径x3,钢管间距x4,翼缘板厚度x5.
3) 水平:①钢管壁厚4~8 mm,②钢管直径181~235 mm,③螺栓直径8~12 mm,④钢管间距250~330 mm,⑤翼缘板厚度4~8 mm.构件设计参数,见图6.
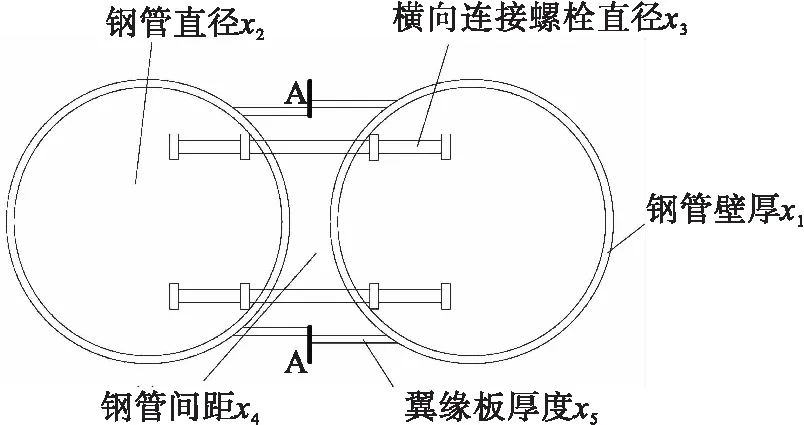
图6 结构设计参数
由数值模拟计算得出评价指标y1和y2,再由式(1)计算得y3,正交试验设计及各组计算结果见表3.
y3=(m1s1+V2s2+m3s3)/lSTS.
(1)
式中:m1为钢管质量(t);s1为钢管每吨单价(元/t)[24];V2为混凝土体积(m3);s2为每立方米混凝土单价(元/m3);m3为螺栓质量(t);s3为螺栓每吨单价(元/t);lSTS为STS管幕构件纵向长度(m).
4.2 正交试验极差分析
由式(2)计算各因素的极差Qk,j(表3中因素xj的指标yk的极差),并通过比较各因素的极差大小来判断该因素对某指标的影响程度;各因素的极差在极差总和的占比越大,影响就越大.
(2)

STS管幕构件达到屈服荷载时的变形y1的极差分析见表4.由表4可知各参数对y1的影响程度,其中y1受钢管直径影响最大,极差占54.85%,增加钢管直径,y1呈减小趋势;其次是钢管壁厚(20.79%)、螺栓直径(12.01%)、钢管间距(6.88%),对y1影响最小的是翼缘板厚度(5.48%).考虑降低y1,在未引入经济指标的前提下,STS管幕构件连接参数可取为:钢管壁厚8 mm,钢管直径235 mm,螺栓直径11 mm,钢管间距250 mm,翼缘板厚度6 mm.

表3 构件参数组合及评价指标计算结果

表4 STS管幕构件达到屈服荷载时跨中位移y1的 极差分析
STS管幕构件的纵向抗弯承载力y2对应的极差分析见表5.由表5可知,y2受钢管壁厚的影响最大,极差占45.01%,增加钢管壁厚,y2呈增大趋势; 其次为钢管直径 (34.84%)、 螺栓直径(9.01%)、钢管间距(5.68%),对y2影响最小的是翼缘板厚度(5.46%).考虑适当提高y2,在未引入经济指标的前提下,STS管幕构件连接参数可取为:钢管壁厚8 mm,钢管直径235 mm,螺栓直径11 mm,钢管间距330 mm,翼缘板厚度8 mm.

表5 STS管幕构件的纵向抗弯承载力y2的极差分析
STS管幕构件每延米构件材料平均价格y3对应的极差分析见表6.由表6可知,y3受钢管壁厚的影响最大,极差占45.27%,增加钢管壁厚,y3呈增大趋势;其次为钢管间距(28.13%)、钢管直径(11.02%)、翼缘板厚度(10.61%),对y3影响最小的是螺栓直径(4.97%).从经济性的角度考虑,STS管幕构件连接参数可取为:钢管壁厚4 mm,钢管直径181 mm,螺栓直径8 mm,钢管间距270 mm,翼缘板厚度4 mm.

表6 STS管幕构件每延米构件材料平均价格y3的 极差分析
4.3 正交试验结果分析
由上节的数据分析,分别得出三组对于各自评价指标最优的STS管幕构件连接参数,见表7.
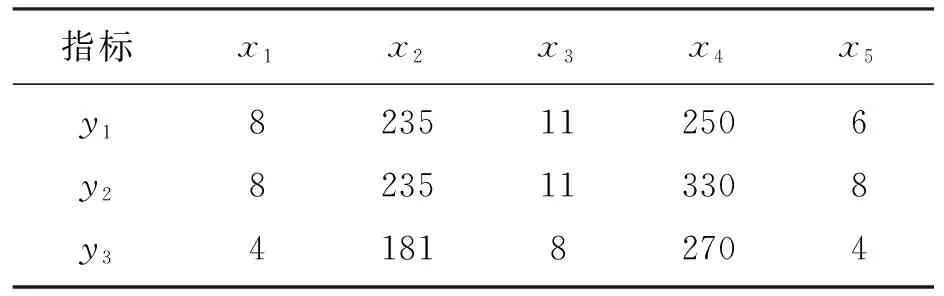
表7 仅考虑各自指标时的最优组合
可见参数取值方面存在矛盾,实际工程中需要综合考虑结构的安全性和经济性等各方面问题.因此,本文引入模糊数学理论优化STS管幕构件的连接参数,以得到兼顾安全性和经济性的参数组合.
5 多指标参数优化模糊分析
5.1 综合评价参数确定
应用模糊数学理论来定义评价指标的隶属度函数.本次正交试验中,y1和y3为偏小型指标,y2为偏大型指标.
对偏小型指标yk,第i次试验时,因素xj的隶属度fik定义如下:
(3)
对偏大型指标yk,第i次试验时,因素xj的隶属度fik定义如下:
(4)

根据式(3)、式(4)计算各次试验的各评价指标的隶属度值,再由隶属度值构成模糊关系矩阵G=(fik)25×3.通过对比三个评价指标各自的重要程度,可以得出一组总和为1的评价指标权重值:
ω=[ω1,ω2,ω3]T.
(5)
STS管幕结构施工应满足上述安全性指标、可行性和经济性指标.本文根据各评价指标的重要性,采用层次分析法对指标权重值进行取值,结果为
ω=[0.31, 0.53, 0.16]T.
(6)
模糊综合评价隶属度的计算公式为
t=G·ω.
(7)
t=[t1,t2,…,t25]T.取ti最大值对应的试验组为正交试验组中最优方案.
5.2 模糊综合评价计算及分析
根据模糊数学理论,由正交试验各因素的隶属度得到模糊综合评价隶属度ti,见表8.

表8 模糊综合评价隶属度ti
第25组正交试验的模糊综合评价隶属度在正交试验组中为最大的,故该正交试验组中的最优组合为第25组.本文对模糊综合评价隶属度ti做极差分析以寻找25组正交试验之外的最优化组合,见表9.
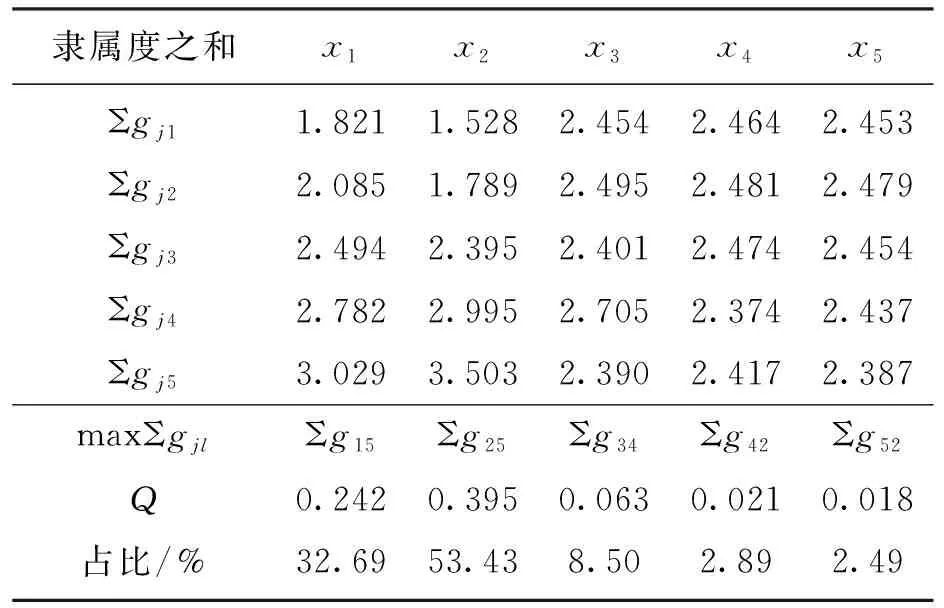
表9 模糊综合评价隶属度极差分析
由表9可知各因素对综合评价的影响程度依次为:钢管直径(53.43%)、钢管壁厚(32.69%)、螺栓直径(8.50%)、钢管间距(2.89%)、翼缘板厚度(2.49%).将模糊综合评价隶属度极差最大值对应的参数水平分别赋给STS管幕构件,则最优参数组合为:钢管壁厚8 mm,钢管直径235 mm,螺栓直径11 mm,钢管间距270 mm,翼缘板厚度5 mm.此时需重新建立有限元模型进行验算.
5.3 优化组合参数验算
5.3.1 优化组合的数值模拟计算结果
构件采用上述优化参数时,计算结果为:y1=4.45 mm,y2=1 148.56 kN,y3=519.38元.优化后的STS管幕构件与优化前的构件LCB-2相比,y1减小14.85%,y2增大45.64%,该优化方案有效控制了结构的变形能力,并提高了结构的承载力.
5.3.2 优化组合的综合隶属度计算
由于评价指标y1的最小值发生变化,重新计算y1的隶属度,并按照式(7)重新计算模糊综合评价隶属度ti,见表10.
由式(3)、式(4)计算得到优化后的STS管幕构件参数组合评价指标的隶属度为
g=[1.000 0.985 0.034] .
(8)
根据式(6)、式(7)和式(8)计算得到优化后STS管幕构件参数组合的模糊综合评价隶属度为0.837,与表10中数据对比,优化后的STS管幕构件参数组合的模糊综合评价隶属度最大,故该优化参数组合是合理的.

表10 优化后模糊综合评价隶属度ti
5.4 最优化参数组合对比分析
贾鹏蛟[11]依托STS管幕结构纵向抗弯性能试验,并结合数值模拟提出钢管壁厚和翼缘板厚度的比值在1.00~1.25之间,且相邻钢管间距和翼缘板厚度的比值应在40左右时其受力较为合理.按照本节所提出的参数优化选取方法,在不考虑经济指标y3的情况下,得到的最优参数组合为钢管壁厚8 mm,钢管直径235 mm,螺栓直径11 mm,钢管间距290 mm,翼缘板厚度7 mm,该参数组合能满足文献[11]给出的取值范围.此外,本文引入了经济指标y3,从安全性和经济性的角度,采用模糊数学理论得到了一组进一步优化后的连接参数组合:钢管壁厚8 mm,钢管直径235 mm,螺栓直径11 mm,钢管间距270 mm,翼缘板厚度5 mm.引入经济指标前后STS管幕构件的评价指标计算结果对比见表11.

表11 引入经济指标前后的评价指标对比
由表11可知,在考虑经济指标时,构件的极限承载力虽下降3.79%,但y1降低1.77%,而y3却下降了5.67%,对于大体量工程项目该指标的降低是比较可观的.由此可见,在承载力得到保证的情况下,不仅能很好地控制结构变形,而且也有效降低了工程成本;因此本文所得结论在为STS管幕结构的工程推广上具有一定参考价值.
在实际工程中根据顶管施工要求,钢管直径往往为定值,根据本文研究得到的各参数优化结果比值为钢管直径∶钢管壁厚∶螺栓直径∶钢管间距∶翼缘板厚度=1∶0.03∶0.05∶1.15∶0.02.
6 结 论
1) 建立了STS管幕的有限元计算模型,构件LCB-2的承载力和刚度与试验值分别相差0.43%和4.94%;构件LCB-6的承载力和刚度与试验值分别相差1.33%和0.75%,吻合度较高.
2) 3个评价指标各自均有2个因素较其他3个因素对其具有显著影响.对于STS管幕构件达到屈服荷载时跨中竖向位移,影响显著的因素是钢管直径和钢管壁厚;对于STS管幕构件极限承载力,影响显著的因素是钢管壁厚和钢管直径;对于STS管幕构件每延米构件材料平均价格,影响显著的因素是钢管壁厚和钢管间距.综合来看,对于连接参数影响显著的因素依次是钢管直径、钢管壁厚.
3) 得到了兼顾安全性和经济性的最优连接参数比,即钢管直径∶钢管壁厚∶螺栓直径∶钢管间距∶翼缘板厚度=1∶0.03∶0.05∶1.15∶0.02.
