基于机器学习的拉矫延伸率预测模型及数值分析
2022-03-08韩烬阳唐晓垒夏搏然
陈 兵, 韩烬阳, 唐晓垒, 夏搏然
(北京科技大学 机械工程学院, 北京 100083)
拉伸弯曲矫直机是带钢冷轧生产线上的重要生产设备,其作用是为了改善产品板带形貌指标(板形),提高产品机械力学性能(消除屈服平台),以及提高来料氧化铁皮机械破鳞效率,因此酸轧拉矫机在现实工程中使用频繁[1].然而,在冷轧板带生产过程中,如果拉矫机工艺参数设置不合理,会导致带钢延伸率不达标,严重影响带钢破鳞效果和板形质量[2],对企业经济效益造成较大的影响.但是,从力学角度对延伸率进行建模预测或者对延伸率进行有限元仿真分析往往基于连续介质假说,最终结果与生产实际存在一定偏差,即使依托大量生产实践得到的经验公式也难以符合生产实际.机器学习算法不用先验性假设,仅从数据本身寻找规律,继而进行数据预测,其预测精度高于常规理论模型计算精度[3];但不同的机器学习算法得到的预测精度也不同.如何在众多算法中找到更适合生产现场的算法,并设定算法的相关超参数,提升算法预测精度一直是困扰众多学者的问题.
根据国内外已公开的文献资料可知, Huh等[4]采用弹塑性有限元法研究不同拉矫参数对带钢延伸率和残余应力的影响,发现不同的网格尺寸对分析结果的影响很大,其中不同尺寸下的应变最大相差了两倍;只有经过多次划分,才能得到网格无关性的近似精确解.Zhou等[5]指出,延伸率是由张力和弯曲曲率共同决定的,利用变形功的计算可以帮助设置张力和弯曲曲率从而调节延伸率.马伟然等[6]利用BP神经网络良好的非线性映射能力,在给定带钢规格等相应的输入参数后,可以输出拉矫所需的插入深度,实现了拉矫参数的设定.张清东等[7]采用MARC有限元软件分析“两弯两矫”的变形过程,利用拟合回归法对拉矫机工艺参数进行拟合预测,建立了延伸率和张力的预测模型.Mathieu等[8]利用有限元软件对带钢输送拉矫过程进行数值模拟,并考虑壳单元离散和辊子之间的摩擦接触,预测最终的带钢形状.
综上所述,当前众多学者主要利用解析模型求解拉伸弯曲矫直过程中的带钢延伸率或者基于弹塑性有限元法建立仿真模型[9],或者利用BP神经网络建立预测模型,对带钢延伸率进行预测;但是针对预测模型精度的研究较少,尤其是在建模时未考虑各参数的相关性,因此模型精度低[10],不能满足企业实际生产要求.本文采用数值解析模型、支持向量机及BP神经网络算法预测带钢延伸率,充分比较了基于弹塑性力学理论的解析模型与机器学习预测模型,分析了两种模型产生差异的原因;利用Adam方法进一步提高神经网络预测精度,利用遗传算法对支持向量机参数进行优化,并比较了各种算法的预测精度.模型经过较长时间的上线运行考核,现场生产数据表明,本文所提出的优化算法可显著提高冷轧板带生产线拉矫工艺参数模型的预测精度.
1 数学解析算法
本文以国内某钢铁企业的宽幅冷轧薄板酸轧生产线拉伸弯曲矫直机组传动系统为例进行研究.图1为典型的“两弯一矫”型拉伸弯曲矫直机组成示意图,图中的A区表示入口张紧辊组,B区表示弯曲及矫直辊组,弯曲辊组可以上下运动,实现工作辊的插入深度调整,C区表示出口张紧辊组.
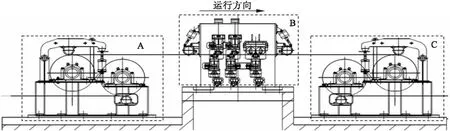
图1 拉伸弯曲矫直机拉矫过程示意图
带钢在过拉矫机进行弯曲变形过程中,由于带钢的弹性,其弯曲半径要大于弯曲辊的辊面半径.带钢的实际弯曲半径与张力、插入深度、带钢规格等多个工艺参数呈非线性关系[11],目前还无法从理论上完全确定其解析式,通常做法是通过对现场实测数据进行拟合,得出经验公式[12].因此参考弯曲半径经验公式[13-16]建立如图2所示的带钢拉矫过程中的应力分布图.
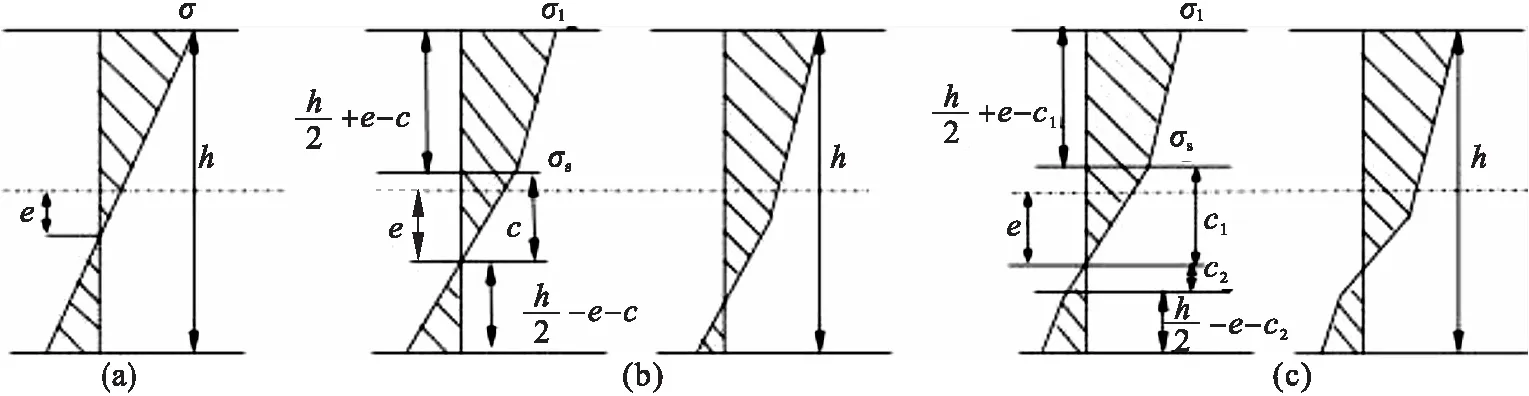
图2 拉矫应力分布图
设定弯曲曲率就是调节设备上弯曲辊和矫直辊的压弯量.当确定了所需的曲率之后,可以根据如下公式确定压弯量[17-18]:
(1)
(2)
(3)
(4)
则中心层应变εr(带钢最终延伸率)为
(5)
(6)
(7)
式中:σF为单位宽度带钢张力所对应的纵向张应力,MPa;F为单位宽度带钢张力,kN;B为带材宽度,mm;h为板带钢厚度,mm;εc为带材表面应变;σs为屈服强度,MPa;ρ为带钢的弯曲曲率半径,mm;d为弯曲辊直径,mm;θ为带材在弯曲辊上的实际包角,rad;δ为插入深度,mm;α为调整系数;E为材料弹性模量,MPa;e为中性层偏移量,mm;εs为带材屈服极限应变;ε0为带材所受的张力应变;E1是材料的加工硬化指数;t为带材厚度,mm;Zs为弹性区高度,mm.
通过上述公式可建立带钢过拉矫机时延伸率的解析模型.以国内某酸轧薄板带生产线实际生产的板带产品为例,该生产线典型产品参数范围为:带钢屈服强度191~660 MPa;带钢厚度1.5~6.0 mm;带钢宽度830~2 000 mm.将生产现场实际工艺参数代入计算模型,随机选取30个样本,其计算值与真实值的比较结果如图3所示.误差为计算结果值与带钢真实延伸率值的差值.
由图3可知,延伸率误差在0附近波动,且波动较大.采用拟合优度R2和均值绝对百分比误差MAPE来评估解析模型精度:R2越接近1,表示预测值对真值的拟合程度越好;MAPE越小,表示模型精度越高,误差越小.计算模型的拟合优度R2为0.734,均值绝对百分比误差MAPE为23.3%.其中,
(8)
(9)

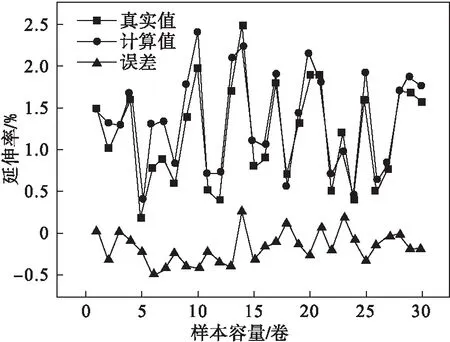
图3 延伸率对比图
综上可得,利用公式计算所得的延伸率与实际生产数据之间存在较大误差,R2小于0.75,MAPE大于23%;因此选用较优方法建立优化模型预测延伸率非常必要.本文提出利用机器学习算法对拉矫机工艺数据建立回归模型,用以预测板带钢延伸率.
2 拉矫生产工艺数据预处理
本文从拉矫生产工艺数据入手,从大量生产数据中寻找规律,建立延伸率预测模型.相关数据来源于国内某钢铁企业的宽幅薄板带酸轧生产线连续生产4个月的数据,如表1所示.其中,强度、宽度、速度指标分别为带钢的屈服强度、带钢宽度和带钢运行速度.张力为拉矫机对带钢施加的张力.辊1、辊2、辊3深度分别为拉矫机的三个工作辊的插入深度.
在分析大数据前,对生产数据进行预处理,剔除影响权重较小的因素和数据中存在的异常值,以减小预测模型的误差.各变量之间相关程度通过计算它们的相关系数进行评定.Perason相关系数一般用于分析两个连续型变量的相关关系,是最常用的方法.
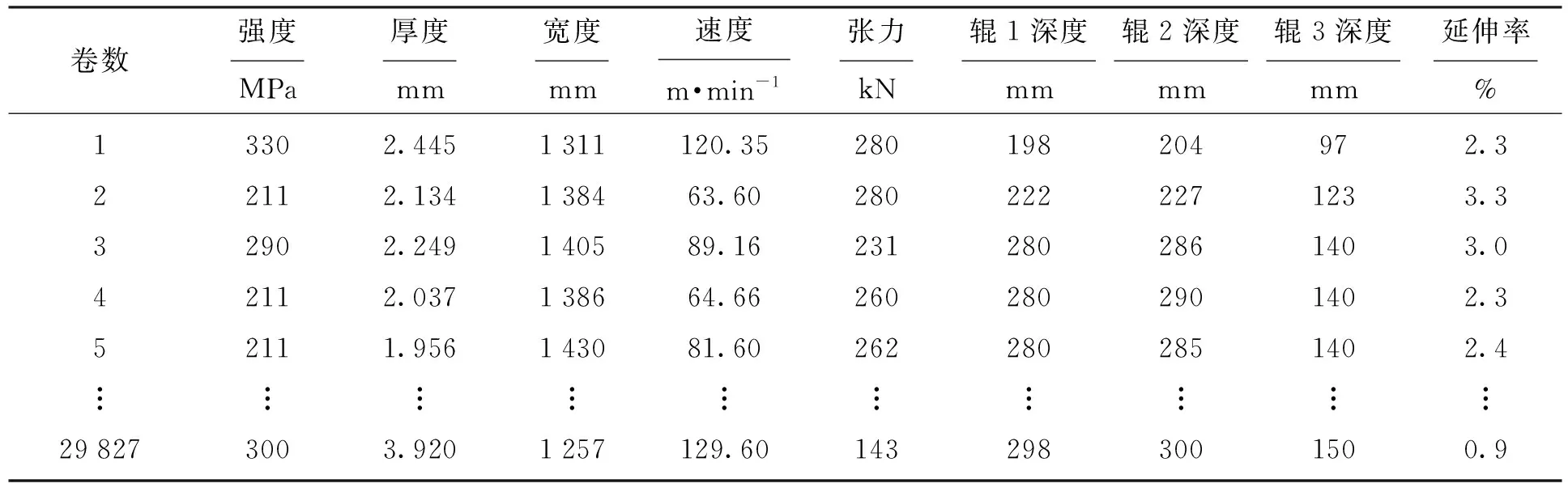
表1 生产数据
若随机变量X和Y的联合分布是二维正态分布,xi和yi分别为n次独立观测值,则相关系数r的公式定义如下:
(10)
|r|≤1,|r|越大,则两变量的相关程度越强;若|r|=1,则两变量完全相关.
计算各个变量与延伸率之间的相关系数,结果如表2所示,数值越大表示相关性越强.从表中可以看出部分变量之间有着较强的相关性.

表2 各变量与延伸率之间的相关系数
将|r|≥0.3的特征进行筛选处理,删除冗余变量宽度、速度和张力.筛选之后的因素包括带钢屈服强度、带钢厚度及两弯一矫型拉矫机最关键的工艺参数(2个弯曲工作辊及1个矫直工作辊的插入深度值).
运用箱线图检验法识别各个特征中的异常值,如图4所示.强度因素识别出高于上界的异常值;3个工作辊插入深度均存在异常值.
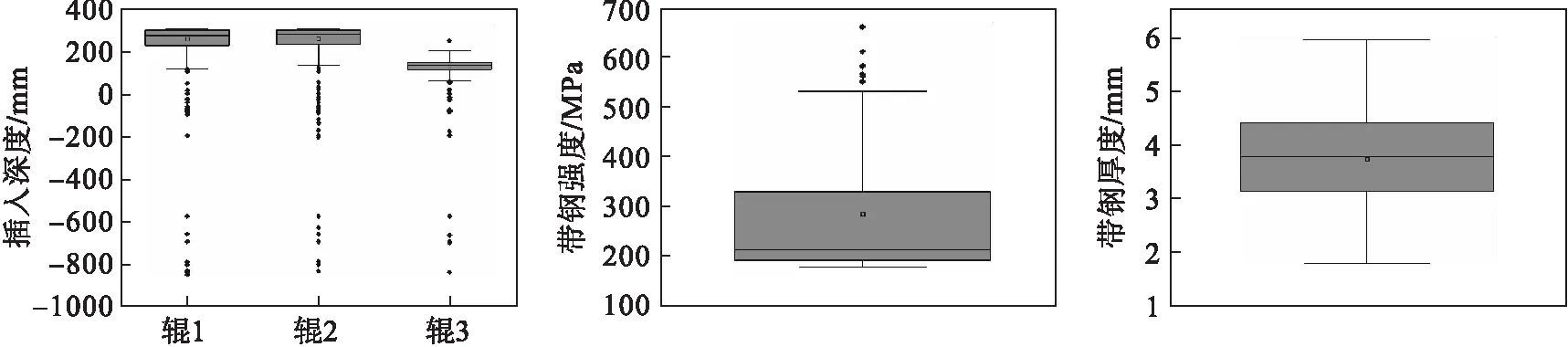
图4 各参数的箱线分析图
3 延伸率预测模型
3.1 预测模型及优化
根据前文中对不同工艺参数相关性的分析、异常数据的剔除及数据标准化的处理结果,研究带钢延伸率预测模型.对基于不同机器学习算法的延伸率预测模型进行比较,在此基础上,择优选择拉矫机延伸率预测模型最终方案.用BP神经网络及支持向量机(SVM)回归算法对大量生产数据进行模型预测试算,继而建立回归预测模型,其中BP神经网络是一种有监督的学习算法,由前向计算和误差反向传播算法组成多层前馈式网络.SVM是一种基于统计学习理论的机器学习算法.SVM为凸二次优化问题,能够保证模型找到理论上的最优解;它的优点在于能够很好地利用映射关系将低维空间中的非线性问题转变为高维空间中的线性问题,降低构建模型的难度,同时提高模型的精度.
图5为基于BP算法和基于SVM算法的预测模型得到的延伸率预测曲线.MAPE和R2作为判定模型预测精度的指标.

图5 两种算法预测结果比较
将延伸率预测结果代入式(8)和式(9),分别算出R2和MAPE:BP算法R2和MAPE分别为0.899和15.4%;SVM算法R2和MAPE分别为0.903和15.3%.BP算法预测精度和SVM算法预测精度相近,比之前理论模型的预测精度高;但两种算法的R2值均没有达到0.95.为进一步提升模型精度,采用Adam算法对BP神经网络的权重值进行优化,记为BP+Adam预测模型;采用遗传算法(GA)对SVM的参数进行优化,记为SVM+GA预测模型.
图6表示利用Adam算法对BP神经网络模型优化后得到的延伸率预测值及其与真实值的误差曲线,可以看出误差曲线的波动较小,拟合效果优于未经优化的BP模型.

图6 优化后BP算法得到的预测曲线
采用遗传算法对SVM进行优化,其中SVM采用高斯核函数,优化的参数为惩罚系数C,宽度系数gamma,和epsilon参数.遗传算法的适应度取值为模型在测试集上的R2,适应度越高越好.其中优化算法的流程图如图7所示.
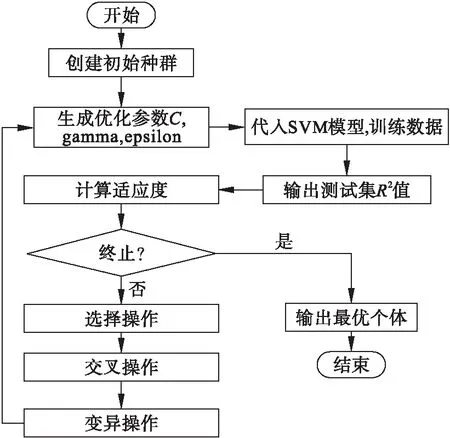
图7 遗传算法优化SVM模型流程图
遗传算法的进化曲线如图8所示,可以看出算法最终收敛于最优值.优化后的参数为C=1.32, gamma=0.18, epsilon=0.26.优化后测试集的R2为0.953.
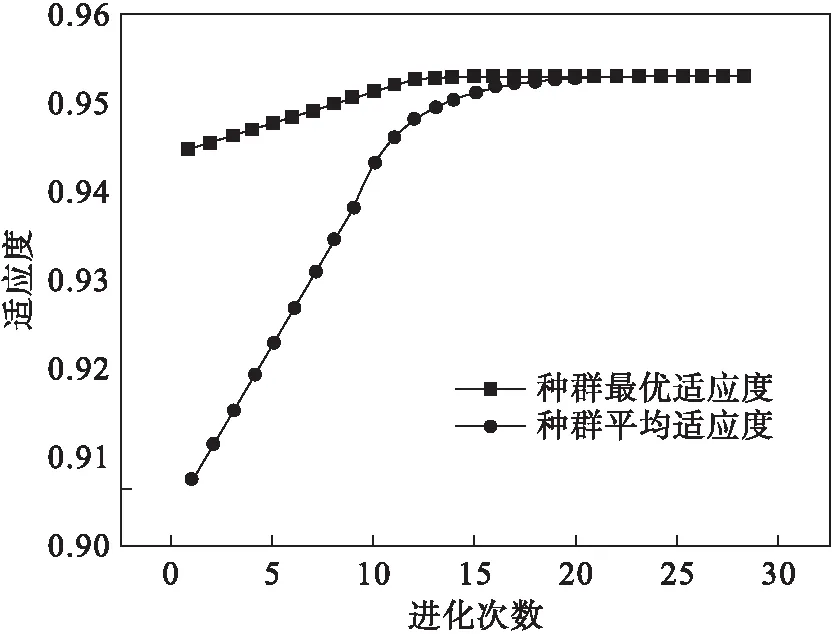
图8 遗传算法进化曲线
将遗传算法得出的最优参数代入SVM模型中进行数据拟合.图9为采用遗传算法优化后的SVM模型预测曲线.由图中可以看出误差曲线的波动进一步减小,拟合效果优于使用Adam算法优化的BP模型.
3.2 模型精度分析
将理论计算模型、基于机器学习的预测模型及其优化的预测模型进行比较,结果如表3所示.
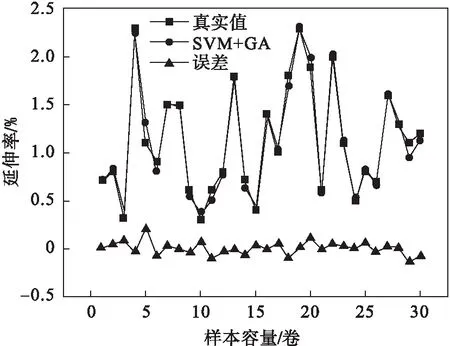
图9 遗传算法优化SVM后得到的预测曲线
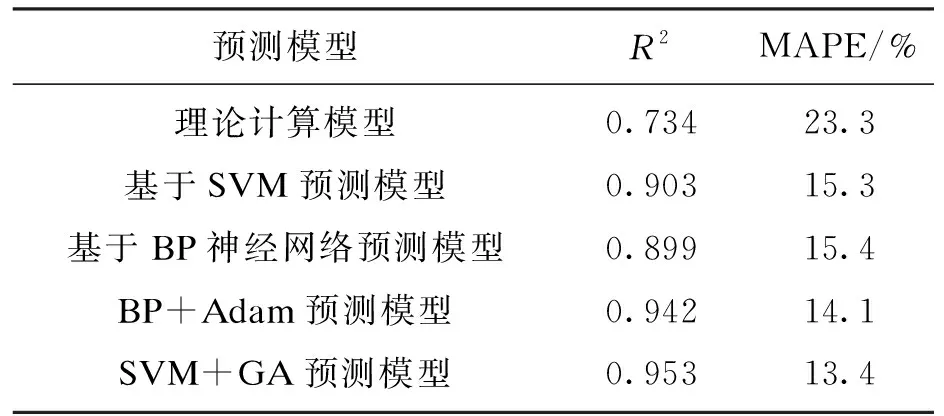
表3 预测模型的精度和误差
由表3可见,拟合优度最高的模型为SVM+GA,R2达到了0.953,远远高于最初未经优化的SVM模型,而MAPE降低到13.4%.BP+Adam模型的预测效果也好于优化前的BP模型,R2提高到0.942.
4 结 论
1) 基于机器学习算法的延伸率预测模型比传统解析模型的拟合优度R2提升了0.219,均值绝对百分比误差MAPE降低了9.9个百分点.
2) 传统计算方法从工艺角度出发,考虑的因素为屈服强度、厚度、张力,以及三个工作辊插入深度,据此预测延伸率;而机器学习模型从生产大数据出发,仅考虑对预测模型相关系数影响较大的因素,模型预测精度优于传统解析模型.
3) 采用遗传算法优化的SVM预测模型拟合优度R2比优化前SVM模型提升了0.050,均值绝对百分比误差MAPE降低了1.9个百分点,优化后的SVM模型和BP神经网络模型均获得了较好的预测效果.
