基于分形理论研究RTSF混凝土冲击压缩性能
2022-03-08王瑜婷陶云霄
陈 猛, 王瑜婷, 陶云霄, 王 浩
(1. 东北大学 资源与土木工程学院, 辽宁 沈阳 110819; 2. 中国水利水电科学研究院 水资源研究所, 北京 100038)
废旧橡胶轮胎的焚烧和掩埋处理会污染空气和占用土地资源,合理利用废旧橡胶轮胎材料有较大的社会效益[1-2].从废旧橡胶轮胎中回收的钢纤维(recycled tyre steel fiber,RTSF)长度分布和几何形状不同于工业钢纤维(industrial steel fiber,ISF),国内外学者将RTSF加入到混凝土中,研究RTSF对混凝土工作性能和力学性能的影响.Caggiano等[3]发现RTSF与混凝土的黏接强度主要与纤维长度有关.另外,RTSF能够有效抑制混凝土裂缝的开展,提高混凝土的抗压强度、韧性和变形能力[4-6],RTSF最优体积分数在0.5%~1.0%之间[7].端钩型钢纤维能够改善混凝土的冲击破坏形态[8-9],掺入体积分数1%的ISF,可以有效提高混凝土的抗冲击能力[10],而目前对RTSF混凝土的研究主要集中在静态力学性能方面[11-12],对RTSF混凝土在冲击荷载作用下的破坏模式和作用机理仍需进行系统分析.
在冲击荷载作用下,混凝土破碎成不同尺寸的碎块,利用分形理论由质量-尺寸关系计算相应的分形维数[13-15],建立混凝土的宏观损伤与力学性能之间的关系.尹跃刚等[16]利用分形理论对混凝土的动态力学特性进行研究,发现混凝土动态压缩强度随冲击破坏分形维数的增大近似呈线性增长.李启帆等[17]研究了钢纤维混凝土冲击破坏时表面裂纹的分形特征,拟合了动态抗压强度、冲击韧度与分形维数的变化关系式.利用分形理论研究材料损伤特征主要是通过盒维数法分析碎块质量和粒径分布的关系[18],而裂纹扩展及能量耗散与碎块数量直接相关,建立基于碎块数量的分形维数可以更准确地分析冲击荷载下混凝土的力学性能.
本文采用直径100 mm的分离式霍普金森压杆(split Hopkinson pressure bar,SHPB)对普通混凝土(F0)、ISF混凝土和不同掺量的RTSF混凝土进行动态冲击压缩试验,对碎块数量进行分级统计,并进行分形特征分析,揭示RTSF掺量和应变率对混凝土分形维数和损伤状态的影响规律,分析RTSF混凝土动态抗压强度及断裂能与分形维数的关系.
1 试验概况
1.1 原材料及配合比
采用P.O 42.5硅酸盐水泥;细骨料为细度模数2.25的天然河砂,密度为2.56 g/cm3;粗骨料为5~10 mm的连续级配花岗岩碎石;减水剂为减水率38%的聚羧酸高效减水剂.RTSF和ISF形貌见图1,物理及力学性能见表1,RTSF长度分布情况见图2.

图1 RTSF和ISF形貌图
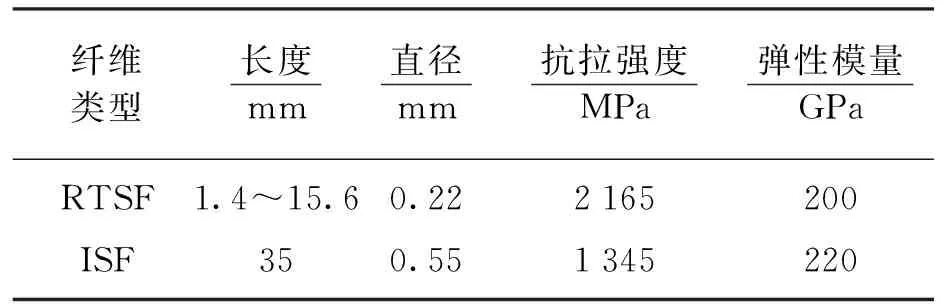
表1 纤维物理及力学性能
混凝土配合比为:水泥477 kg,砂485 kg,碎石1 283 kg,水200 kg,减水剂4 kg;RTSF掺量分别为39,59,78和98 kg(体积分数分别为0.50%,0.75%,1.00%和1.25%),材料编号分别为RTSF 0.50,RTSF 0.75,RTSF 1.00和RTSF 1.25;ISF掺量为78 kg(体积分数为1.00%),材料编号为ISF 1.00.
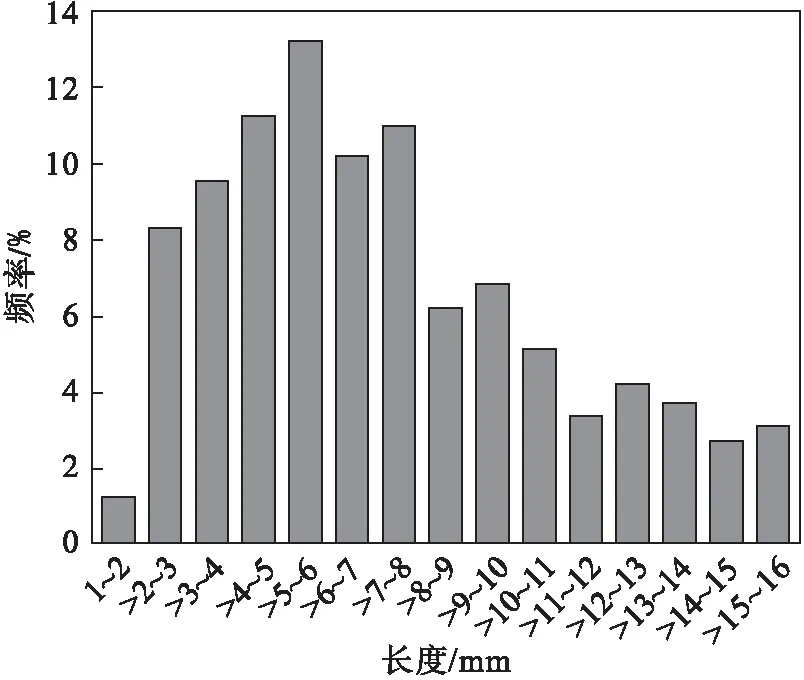
图2 RTSF长度分布频率图
1.2 试件制备
按照配合比将粗骨料、细骨料和水泥放入搅拌机中干拌2 min,然后倒入水和减水剂湿拌2 min,最后加入RTSF或ISF搅拌3 min至纤维分散均匀.将混凝土拌合物装入直径100 mm、高度50 mm的圆柱体试模,振捣密实后静置24 h后拆模,标准养护至28 d.取出试件后对其上下底面进行磨平加工,保证试件两端面不平整度在0.05 mm以内.
1.3 试验设备及方法
SHPB装置(如图3所示)的撞击杆、入射杆、透射杆和吸收杆(长度分别为600,5 000,3 500和1 200 mm)均为直径100 mm的高强合金钢,弹性模量为209 GPa,密度为7 850 kg/m3.采用直径为50 mm、厚度为2 mm的橡胶片作为波形整形垫片,冲击压缩试验的应变率范围约为55~125 s-1.
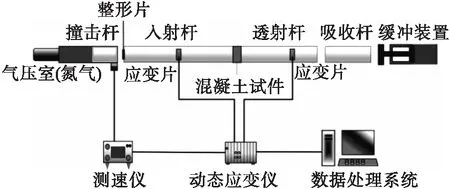
图3 SHPB试验装置示意图
收集冲击试验后的混凝土碎块,碎块质量总和与原试件质量误差在5%范围内.选用尺寸为35,19,9.5,4.75,2.36和1.18 mm的标准方孔筛进行筛分,通过精度为0.1 mg的电子称称量筛上滞留碎块质量.统计不小于4.75 mm的各级碎块数量,对小于4.75 mm的各级碎块以一定数量进行称重,得到碎块平均质量随碎块数量的变化趋势,估算各级尺寸碎块的数量.
2 冲击破坏块度的分形特征
2.1 破坏形态
表2为不同应变率下混凝土的冲击破坏形态.随着应变率的增加,试件中裂纹增多,混凝土的破碎程度不断加剧.当应变率从55 s-1增至75 s-1左右时,试件周围出现张应变破坏,混凝土内部裂纹逐渐发育,F 0和RTSF 0.50试件出现边缘裂开和脱落破坏,RTSF 0.75,RTSF 1.00,RTSF 1.25和ISF 1.00试件周围仅出现少量大尺度碎块,表明RTSF和ISF能够抑制裂纹的开展;当应变率从95 s-1增至110 s-1左右时,混凝土试件周边破碎,中间部分保持完整,纤维出现脱黏失效,拔出基体(见图4),即留芯破坏形态;当应变率为125 s-1左右时,F0试件破碎成松散的颗粒,表现为整体破坏.冲击压缩过程中,混凝土试件的损伤裂纹由外部向内部扩展,原因是内部混凝土受外部混凝土的约束.高应变率时,混凝土由于抵抗冲击能量而产生的裂纹数量增多[19-21],裂缝扩展并伴随纤维拔出,直至试件完全破坏.

图4 裂缝处的RTSF和ISF
2.2 分形维数
混凝土由于内部存在孔隙和微裂纹,破碎时碎块的分布状态和几何形状在一定的测量范围内具有自相似性[13,19].对RTSF混凝土破碎后的碎块进行分级统计,对比不同粒径下的碎块形貌(见图5)发现RTSF混凝土碎块存在自相似性,即具有明显的分形特征.

表2 冲击压缩试验不同应变率下混凝土的破坏形态

图5 不同孔径标准筛上碎块形貌图
分形维数与碎块的块度分布具有密切关系,分形维数越大,裂纹在破坏过程中扩展贯通越充分,对应试件的破坏情况越严重.分形维数Db为
Db=logxN-1.
(1)
式中N为粒径大于x的碎块个数.
图6为各材料在不同应变率下分形维数随粒径的变化图.不同应变率下F 0在4.75 mm粒径时的分形维数最大;当应变率为55 s-1和75 s-1左右时,RTSF混凝土和ISF 1.00分别在1.18 mm和2.36 mm粒径时分形维数最大;应变率达到95 s-1左右时,RTSF和ISF混凝土的分形维数在4.75 mm粒径时最大.当应变率从55 s-1增至95 s-1左右时,RTSF和ISF混凝土分形维数最大值的对应粒径随应变率增大而增大,说明在较低应变率时RTSF和ISF可有效降低混凝土的破碎程度.取不同应变率对应的最大分形维数作为该材料的分形维数代表值,可得应变率在55~125 s-1左右时F 0,ISF 1.00,RTSF 0.50,RTSF 0.75,RTSF 1.00和RTSF 1.25的Db最大值变化范围分别为1.83~2.30,1.35~2.09,1.37~2.23,1.33~1.94,1.36~2.19和1.43~2.25.
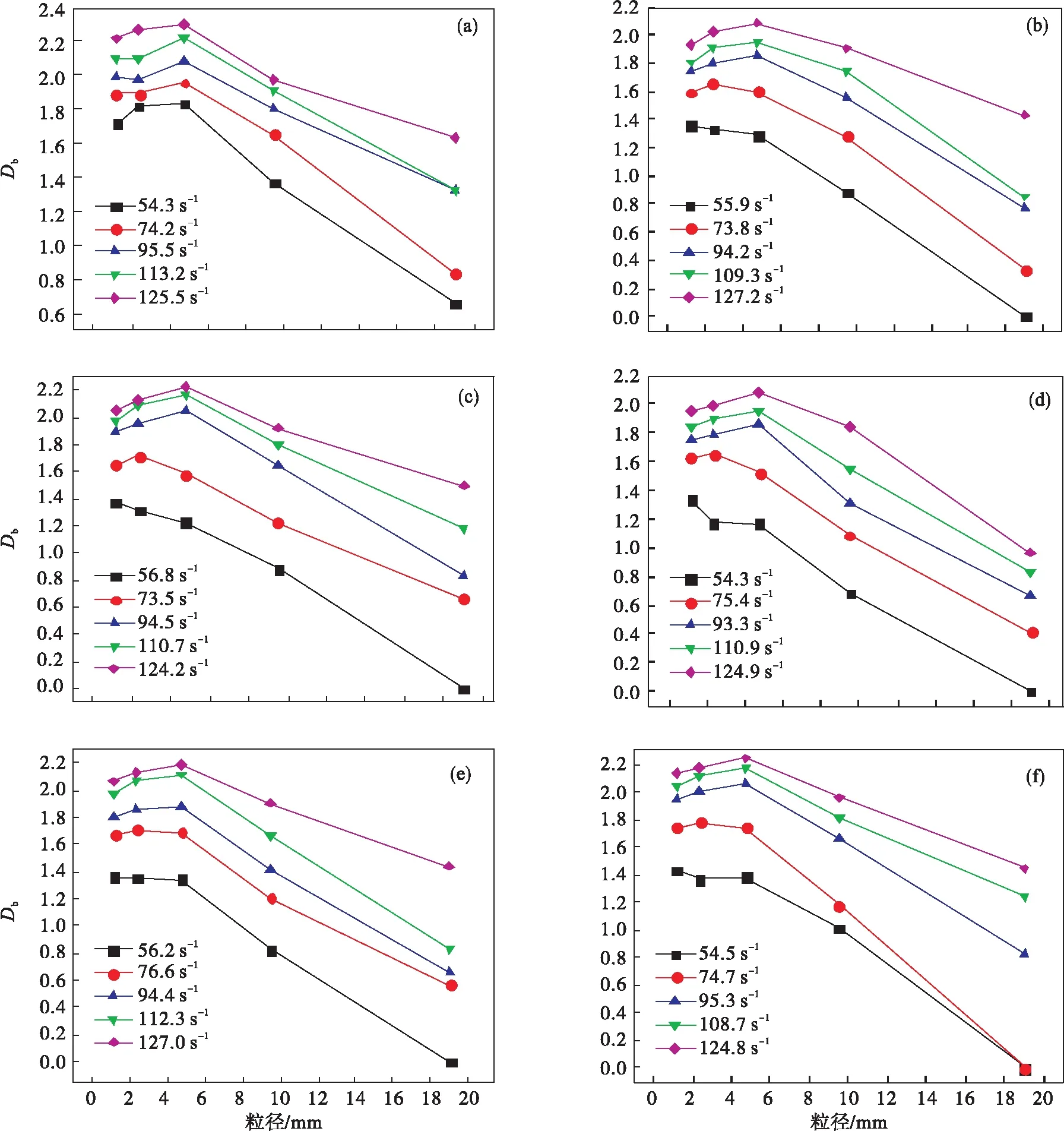
图6 不同应变率混凝土的分形维数随粒径的变化
2.3 应变率对分形维数的影响
图7为不同材料的分形维数随应变率的变化图,不同材料的分形维数随着应变率的增加而增大,具有明显的应变率效应[16],这是因为混凝土在冲击荷载下由一维的应力状态向一维应变状态转变[20],试件在短时间内微裂纹的数量迅速增加,试件破坏时碎块尺度减小,数量增多,分形维数增大.当应变率从55 s-1增至125 s-1左右时,F 0,ISF 1.00,RTSF 0.50,RTSF 0.75,RTSF 1.00和RTSF 1.25的分形维数增幅分别为25.4%,53.7%,62.1%,44.4%,60.5%和56.6%,其中RTSF 0.75的分形维数增幅在RTSF混凝土中最小,此掺量下混凝土受应变率影响最低.在应变率为55 s-1左右时,RTSF降低混凝土分形维数的效果较为明显,比F 0表现出更好的抗裂性能.当应变率在125 s-1左右时,ISF 1.00,RTSF 0.50,RTSF 0.75,RTSF 1.00和RTSF 1.25的分形维数相对于F 0分别降低了9.2%,3.2%,16.0%,4.7%和2.4%,说明在较高应变率下RTSF和ISF均可有效降低混凝土的损伤破坏.不同应变率下ISF 1.00分形维数介于RTSF 0.75和RTSF 1.00之间,说明体积分数0.75%的RTSF能更有效地提高混凝土的抗冲击破坏能力.
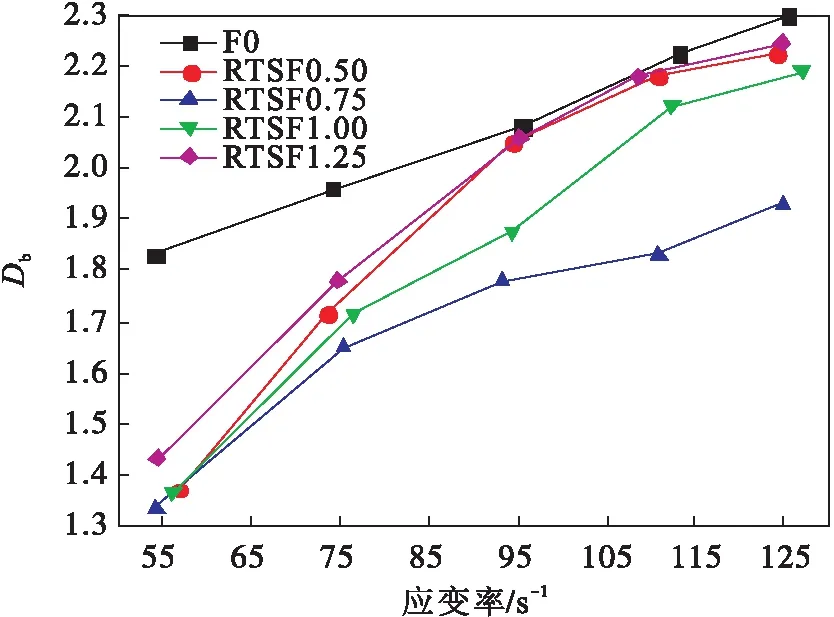
图7 不同材料分形维数与应变率的变化关系
2.4 纤维掺量对分形维数的影响
图8为不同应变率下RTSF混凝土分形维数随纤维掺量的变化图.不同应变率下,混凝土的分形维数随RTSF掺量的增加出现先减小后增大的趋势,RTSF体积分数为0.75%时分形维数最小,这是因为一定掺量的RTSF可以与混凝土基体有效黏结,在冲击荷载作用下发挥“桥连”作用[21],抑制基体裂缝的开展,降低混凝土的破坏程度;另一方面,当RTSF体积分数过大时,混凝土纤维与浆体的薄弱界面增多,产生了更多可供气体进入的通道,增大了混凝土的含气量[7],对混凝土的工作性能和力学性能产生不利影响.
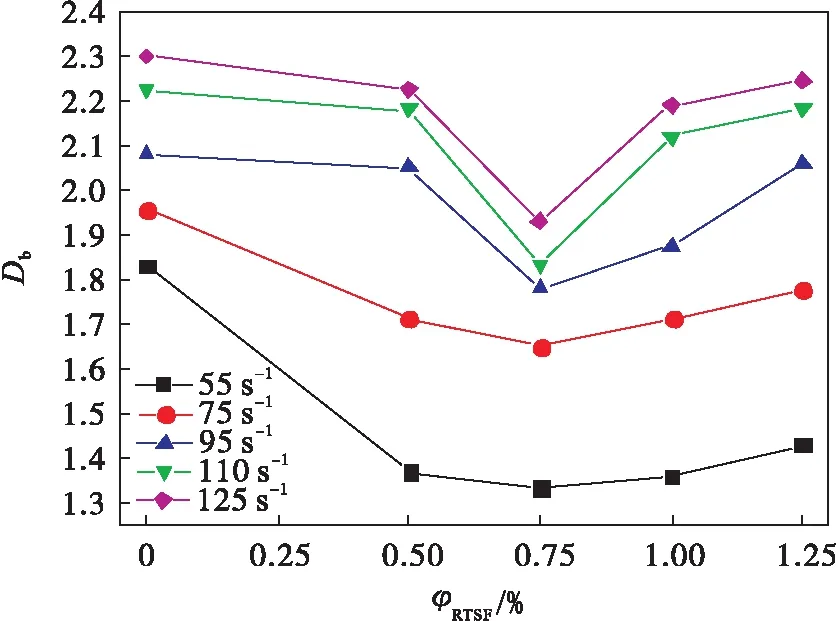
图8 不同应变率下混凝土分形维数与RTSF掺量的 变化关系
2.5 动态抗压强度与分形维数的关系
图9为不同材料的动态抗压强度随分形维数的变化图,各材料的动态抗压强度随着分形维数的增加而增大.在冲击荷载作用下,混凝土内部没有足够时间积累能量来抵抗变形,只能通过增加内部应力和裂纹抵抗冲击能量[22],RTSF延缓了裂纹扩展,提高了混凝土的动态抗压强度.
当分形维数为1.36~1.86时,ISF 1.00与RTSF 1.00的动态抗压强度相差不大;分形维数超过1.86时,ISF 1.00的动态抗压强度大于RTSF 1.00,即相同动态抗压强度时,ISF 1.00破坏程度小于RTSF 1.00.当分形维数为1.33~1.94时,RTSF 0.75的动态抗压强度最大,说明在该分形维数范围内体积分数为0.75%的RTSF提高混凝土强度的效果最明显.
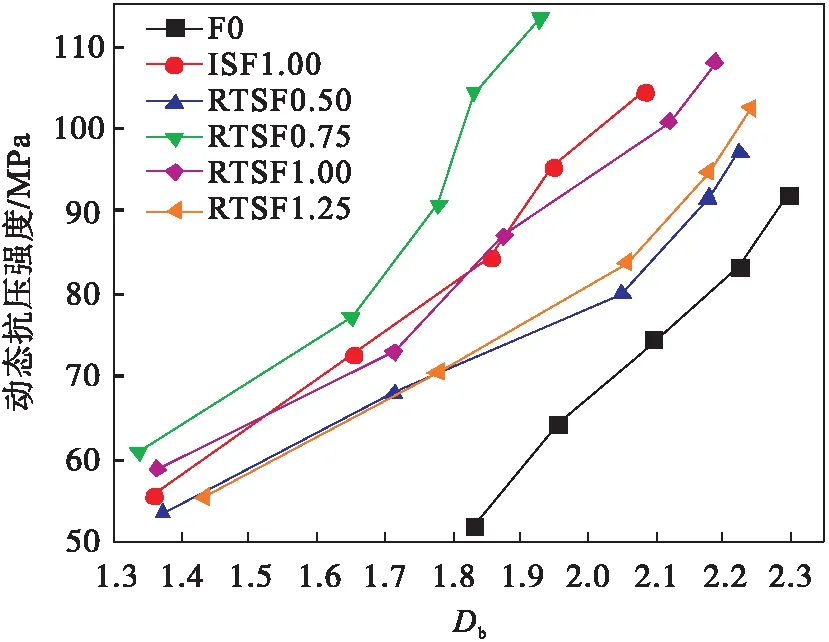
图9 混凝土的动态抗压强度与分形维数的变化关系
2.6 断裂能与分形维数的关系
断裂能为试件在SHPB试验中达到峰值应力时所吸收的能量[23],图10为不同材料的断裂能随分形维数的变化图,可见不同材料的断裂能随分形维数的增加而增大,这是因为裂缝的产生和扩展使桥连在裂缝处的纤维从混凝土基体中滑移拔出,提高了混凝土断裂能.随着分形维数的增大,F 0,RTSF 0.50和RTSF 1.25试件在维持一段能量平衡后进入能量储存阶段,该阶段材料的分形维数增大而能量变化较小,这是混凝土应变硬化的表现.断裂能在150~180 J左右时,能量逐渐耗散,造成材料劣化[18],混凝土强度丧失;而RTSF 0.75,RTSF 1.00和ISF 1.00的断裂能随分形维数增大呈线性增长,表明此时纤维与混凝土基体在试件断裂过程中可以均匀发挥作用.
当分形维数为1.33~1.94时,RTSF 0.75的断裂能最大,说明RTSF 0.75的能量耗散能力最强.在相同分形维数时,RTSF混凝土比F 0断裂能大,表明RTSF与混凝土相互作用吸收了部分外荷载对试件做的功,提高了材料的吸能能力.当分形维数为1.36~1.86时,ISF 1.00与RTSF 1.00的断裂能变化趋势相似;分形维数超过1.86时,ISF 1.00的断裂能介于RTSF 0.75和RTSF 1.00之间,原因是RTSF的形状为三维弯曲状,在混凝土中具有较大的机械锚固力,在拔出过程中与基体形成较大的摩擦力[24],同时不同长度的RTSF在混凝土中发挥“长短混杂”效应,其中短纤维主要抑制微裂纹的产生,而当微裂纹逐渐扩展时, RTSF混凝土中的短纤维逐渐被拔出,长纤维开始对裂纹产生抑制作用,延长了混凝土被破坏的时间[25].根据纤维体积分数和纤维长度计算出RTSF 0.75的数量约为ISF 1.00数量的3倍,由纤维间距理论可知RTSF 0.75比ISF 1.00能更有效地抑制裂纹的产生和扩展.
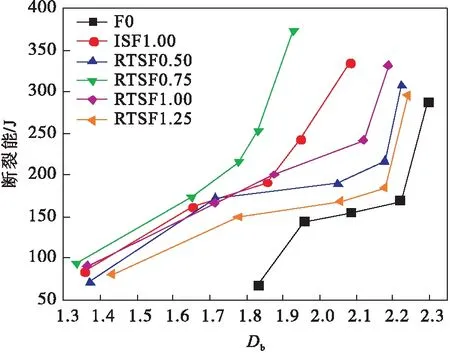
图10 混凝土的断裂能与分形维数的关系
3 结 论
1)冲击破坏后RTSF混凝土碎块具有明显的分形特征.应变率为55~125 s-1左右时,F 0,ISF 1.00,RTSF 0.50,RTSF 0.75,RTSF 1.00和RTSF 1.25的分形维数变化范围分别为1.83~2.30,1.35~2.09,1.37~2.23,1.33~1.94,1.36~2.19和1.43~2.25.
2) RTSF混凝土的分形维数随应变率的增大而增大,具有明显的应变率效应.在相同应变率下,RTSF混凝土比F 0的分形维数小,且随RTSF掺量的增加出现先减小后增大的趋势,RTSF 0.75分形维数最小.
3) RTSF混凝土的动态抗压强度和断裂能均随分形维数的增加而增大,RTSF 0.75的动态抗压强度最大,能量吸收能力最强.
4) ISF 1.00的分形维数、动态抗压强度和断裂能均介于RTSF 0.75和RTSF 1.00之间,掺入体积分数0.75%的RTSF比掺入体积分数1.00%的端钩型ISF(长度为35 mm,长径比为65)更能降低混凝土在冲击荷载作用下的破坏程度.
