基于启发式遗传算法的模糊测试样本集优化方案
2022-03-08王志华王浩帆程漫漫
王志华,王浩帆,程漫漫
(郑州大学 网络空间安全学院,郑州 450002)
随着信息与通信技术的快速发展,信息技术改变了人们的生活方式。然而,伴随而来的网络与信息安全问题也逐渐引起了社会各个领域的广泛关注。
软件漏洞挖掘技术[1]在信息安全领域中占据了重要地位。模糊测试[2]则是漏洞挖掘中较为有效的方法之一,其是一种基于缺陷注入的自动化软件测试技术,主要依赖于不断输入非预期的数据并对数据进行监控和观测的方式发现软件是否会存在异常。传统的模糊测试技术并没有对初始样本集进行处理,而是直接进行变异分析。样本的重复性会产生大量代码率低且无用的测试用例,从而降低了模糊测试的效率。如何改进模糊测试的缺陷已经成为当前研究热点。考虑模糊测试样本集的特点,可以对其进行优化,从而精简样本集的数量,提高样本集的质量,进而提升模糊测试的效率。因此,研究模糊测试样本集的高质量性精简问题,具有很大的理论意义和工程应用价值。本文对模糊测试样本集精简进行了研究,借助0-1矩阵,在遗传算法的基础上进行改进,将贪心逼近算法与遗传算法结合,提出了基于启发式遗传算法的样本集精简解决方案。实验结果表明,本文方法是有效的。
1 相关工作
近年来,众多学者从集合覆盖、机器学习、遗传算法等角度围绕模糊测试样本集的精简问题开展了大量的研究工作。马金鑫等[3]设计了一种贪心逼近的求解算法来优化模糊测试的输入样本集,在样本集覆盖率不变的前提下求解获取最小样本集合;Bhme等[4]把模糊测试问题建模为Markov模型,并采用特定的策略引导AFL优先选择低频路径和变异频率低的文件作为文件进行变异;随后Bhme等[5]提出采用模拟退火算法对能逼近特定目标位置的测试输入分配更高的能量,并优先选取高能量种子文件进行变异;Wang等[6]提出了一种质量感知的测试用例优先级技术,优先输入高质量的种子,直接定义获取高质量的种子;唐枭[7]利用污点分析和其他技术来获取数据的执行路径,对代码覆盖率相关字段进行基因编码,并执行遗传算法的选择变异过程,对危险操作相关字段执行边界值赋值,产生新的测试用例。
在实际处理过程中,采用集合覆盖技术解决样本集的精简或筛选时,精确算法能够找到集合覆盖问题的最优解,近似算法能够取得有质量保证的解,但其求解速度较慢,只能求解较小规模的实例。采用机器学习方法时,需要对数据进行大量的训练并分类,但由于模糊测试样本集的整体性特点,需要人工干预设定指标,反而降低了模糊测试的效率。使用传统的逼近算法可以实现对样本集的缩减,但是没有考虑样本在实际问题中的适用性。
2 基础理论和评价指标
2.1 基础理论
2.1.1 贪心逼近算法
贪心逼近算法[3]是指利用有关算法解决一些实际问题的场景或精确度,且给出的解决方法是理论上的最优解。在样本集的精简中,贪心逼近算法指的是尽可能精确地给出样本的最小样本集,获取优质样本是贪心逼近算法的唯一标准。
2.1.2 遗传算法
遗传算法[8]是一种基于生物进化原理构想出来的搜索最优解的仿生算法。其模拟基因重组与进化的自然过程,把待解决的问题的参数编程成二进制码或十进制码(也可编成其他进制码),即基因,若干基因组成一个染色体(个体)。对染色体进行类似于自然选择、配对交叉和变异运算,经过多次重复迭代(世代遗传)直至得到最后的优化结果。
遗传算法的步骤如下:
步骤1 初始化第0代种群P0。
步骤2 对第i代种群Pi迭代执行步骤2.1~步骤2.5,直到满足停止准则:
2.1 计算Pi中每个个体的适应值,并按照适应值的大小对所有个体进行排序。
2.2 将Pi中适应值最佳的个体加入Pi+1。
2.3 按照适应值的大小排序在Pi中选择2个父体。
2.4 按概率选择杂交算子或者变异算子对两父体进行遗传操作,将生成的个体加入Pi+1。
2.5 如果Pi+1的规模已经与Pi持平,则i←i+1并转步骤2,否则转步骤2.3。
步骤3 将最终种群中适应度最好的个体作为遗传算法的结果。
2.1.3 集合覆盖问题
集合覆盖问题(SCP)[9]:在模糊测试中,任何样本集都可以转化为最小集合覆盖问题,而最小覆盖集为经典的NP-hard问题[10],难以计算最优解。集合覆盖问题形式上可以描述如下:令A=(aij)为一个m行、n列的0-1矩阵。C=(cj)为一个n维整数向量。令M ={1,2,…,m},N ={1,2,…,n}表示矩阵A的行向量和列向量维数。值cj(j∈N)表示某一列的代价。不失一般性,假定cj>0,j∈N。如果aij=1,则认为列j∈N覆盖了行i∈M。集合覆盖问题要求一个最小代价的子集合S⊆N,这样每一行i⊆M 至少被一列j⊆S覆盖。集合覆盖问题的一个自然的数学模型可以描述为:v(SCP)=m incjxj,服从于aijx˙j≥1,i∈M,xj∈(0,1)(j∈N);如果xj=1(j∈S),则xj=0。
2.2 评价指标
1)压缩率。对比样本精简前和样本精简后的测试样本数量,并计算压缩率来表示算法对样本集的优化程度。
2)执行模糊测试所需要的时间。假设模糊测试初始样本集数量为n,模糊测试时间函数为f(n),随着模糊测试数量n的增加,模糊测试执行时间的增长率与f(n)的增长率正相关。
3)样本质量。主要由代码覆盖率为判断依据;代码覆盖率为测试的代码行数占总代码行数的比例。
3 基于启发式遗传算法的样本集优化
样本集的精简是将数量庞大的数据集进行缩减的过程。从本文所解决的问题出发,对于模糊测试集中的样本,样本的重复不仅表现在完全相同的样本,而且从变异的根源来说,样本间基本块的相互覆盖是导致变异产生大量重复测试用例的问题所在。因此,本文在进行样本选取时,规定优先选取包含代码基本块数最多的样本(代码块数多的样本在进行变异时可以得到更多测试用例),再按照样本性能依次选择,直到新样本集基本代码块可以覆盖原始样本集的基本代码块为止。本文要定义的启发式算法是对染色体选择的算法,最终获取所求染色体集合。
3.1 染色体的表示
为了保证在样本集数量最少的基础上得到更优质的样本(基本代码块数多且变异能力好),在实现过程中,引入0-1矩阵[11],向量x的元素是0或者1,用一个n位的二进制串作为染色体结构,n是矩阵A的列数,第i位上的值“1”意味着第i列被选择。
进行模糊测试时,每个程序都有自己所包含的基本代码块,根据基本块地址找到的内容就是对应的代码块。基本块地址信息的获取是比较方便的,故将基本块地址作为研究对象(每个基本地址块相当于遗传算法中的基因)。每个样本看作一个以基本代码块地址为元素的集合(样本相对于遗传算法中的染色体)。样本中如果存在某个基本地址块就用“1”表示,否则用“0”表示,所有的样本构成一个以0或1为元素的0-1矩阵。矩阵中的“1”即表示染色体的基因,每一列基因的集合相当于一个染色体。
3.2 启发式遗传算法改进染色体
选择的染色体都会有自己独特的基因存在,交叉重叠的基因也不计其数。在进行集合覆盖时,需要确定最小覆盖集合并保证该集合冗余最小。
在实际的遗传过程中,由于变异操作产生的染色体并不适合问题集合,本文不再对新个体的变异基因进行修复,而是将变异产生的新个体直接舍弃(由于原始数据较相似,出现新的基因的概率很小)。遗传算法执行后会保留所有产生的染色体,该启发式算法的作用包括以下2点:①消除因为基因重复产生的冗余;②选择更优质的染色体(包含的基因多且基因组合更丰富)。
启发式算法阐述如下:
1)矩阵中的染色体和基因表示。
在0-1矩阵中,一列表示一个染色体,矩阵中的“1”表示某个染色体包含这个基因,“0”表示该染色体不包含该基因。算法使用性能代价比的优先思想:性能指的是染色体中某位基因所对应集合中的列包含“1”的个数,个数越多,则该列覆盖的行数就越多,说明该染色体的性能比较高。假设一组染色体使用遗传算法时产生的所有染色体集合为:Sall={s1,s2,s3,s4,s5},s1={2,4,6},s2={1,6},s3={3,5},s4={2,3,7},s5={1,7}(本文采用数字来表示其包含的基因及位置)。
2)染色体的基因交换。
假设A1和A2是父代的2个染色体,B1和B2是染色体交换之后所得的孩子染色体。可以覆盖矩阵A的集合,借助集合C1和C2,用其来存放基因没有覆盖的行号;集合D1和D2用来存放B1和B2包含的全部基因。例如,A1={s1,s5},A2={s2,s3,s4}集合,B1、B2、C1和C2均为空集,D1={1,2,3,4,5,6,7},D2={1,2,3,4,5,6,7}。
①计算集合A1和A2中每个基因体的性能η,即每列所包含的“1”的个数,“1”越多,表示该染色体能覆盖行越多,其包含的基因就越多,其性能就越高。此时各个基因的性能为:ηs1=ηs4=3,ηs2=ηs3=ηs5=2。
②A1和A2中性能最高的染色体放入集合B1,统计该染色体包含的基因,并在集合D1中将其删除,计算其未包含的基因,将这些基因的行号存入集合C1,再按照相同方法排列A1和A2剩下的基因到B1,最后将其他的基因放入B2。
③在进行基因选择时,可能会出现一些基因性能一样的情况,因此在性能相同的基因中选取最优质的基因是算法设计的关键。例如,假设集合父辈A1中有2个性能一样的基因:s1={2,4,6},s2={1,4,6},当前集合B1中包含一个基因s3={2,3,5,6},s1、s2作为被选择对象,s2和s3中相同的代码块要多于s1和s3的代码块,因此选择s2比s1更合适。除此之外,模糊测试样本在进行变异时,会根据自己的代码块随机变异生成测试用例。例如,s1={2,4,6},s2={1,4,6},当前集合B1中包含一个染色体s3={2,3,5,6}。在染色体s1中,2号和6号代码块在B1中已经出现,代码块进行变异后,相当于产生了一个新的基因组合。s3中,当3号和5号基因不变异时,剩下的2号和6号的基因组合与染色体s1在4号基因不产生变异的基础上是一样的效果。相比较,染色体s2除了4号基因,1号和6号基因在进行变异时会产生新的组合,进而产生新的测试用例。在实现消除冗余的基础上,在进行下一个染色体选择时,会出现性能相同的染色体,但其所包含的基因是不同的;在进行选择前,将等待选择的性能相同的染色体与集合B1中已选的染色体做“差”,记录“差”集的元素个数,按照上述规则,元素个数多的“差”集与已选染色体不相同的个数就越多,那么对应的染色体即为下个候选染色体。
启发式遗传算法在原始种群的基础上借助于0-1矩阵获取所需染色体;在不需要改变遗传算法工作过程的前提下优化搜索条件,提升模糊测试的效率。
3.3 启发式遗传算法实现
启发式遗传算法的实现过程在理论意义上与传统的遗传算法是没有区别的,同样需要重点考虑以下几个方面:①种群大小和种群初始化。种群样本集的大小可以人为控制,而不随机选择。②父代选择。在千万样本集中选择2个样本集作为父代,这是遗传算法仿生物的表现。③交叉率。确定父代在染色体的某个点进行交叉繁殖产生来后代。④变异率。产生后代的方法不仅依靠交叉,变异也是新物种最重要的来源。⑤精英比率。直接进入下一代而不参与基因交换的优秀个体的比例。⑥停止准则。传统的遗传算法需设定界限;样本集合覆盖问题需要设定其遗传的代数,或者某一个子代覆盖了所有测试路径时停止。
1)种群大小和种群初始化。
使用遗传算法解决实际问题时,种群的大小对遗传算法所求得的解的质量有很大影响。适当的种群数量可以提高算法的性能。种群数量过大,影响算法的效率;种群数量过小,整个算法过程起到的作用不大,反而将集合问题复杂化。在样本集精简问题中,本文算法没有对种群的大小进行太多的限制,数量根据实际情况自行定义,但是也会对不同种群数量进行不同的测试,以便粗略地获取较好的种群数量范围。
2)父代的选择。
父代的选择是对种群中每个个体赋予的产生后代的机会。一般选择方法包括随机选择法、锦标赛选择法和轮盘赌注法。本文采用轮盘赌注法,其基本思想是:个体被选择的概率与其适应度大小成正比。具体实现操作如下:
①计算出种群每个个体的适应度fi(i=1,2,…,M,M为种群大小)。

④在[0,1]区间内产生一个均匀分布的伪随机数r。
⑤若r<q1,则选择个体1,否则,选择个体k,使得:qk-1<r≤qk成立。
⑥重复④、⑤共M次。
3)交叉率[12]的选择。
交叉是产生新个体的主要方法,在被选中的父代中确定一个交叉点,使双亲在交叉点进行基因的重组。交叉率是用来设定交叉池中参与交叉的染色体的个数,合理的交叉率可以保证交叉池中不断产生新个体,且不会产生过多的新个体,导致遗传秩序破坏。不同的交叉方法对应着不同的交叉率,当前主流的方案是采用自适应方法。
4)变异率[13]的选择。
变异率指的是一个种群中发生变异的基因数目与全体基因数目的比例。变异是产生新个体的另一种方式,可以通过设定随机变异的基因数也可以设定变异率来控制变异情况。在本文所研究的样本集精简中,变异可以将包含独特基因的染色体提前纳入到所设定的搜索规则中,以便于保证遗传算法的全局性。为此本文采用实验来设定合适的变异率,将最后一条含有独特基因的染色体混入其他染色体,并使用本文提出的启发式遗传算法来进行选择。
图1给出了变异率在0.5、0.6和0.7时待选基因随着初始染色体数量的增加被启发式遗传算法选入的时间变化。由图1可以得出,变异率为0.6时,花费时间最少。变异率过小会导致参与变异的染色体过少,并不能将含有独特基因的染色体提前录入集合;变异率过高将会使得参与变异的染色体过多,更容易产生一些非法的数据并且增大时间开销。因此,综合考虑后,本文启发式遗传算法选取的变异率为0.6。
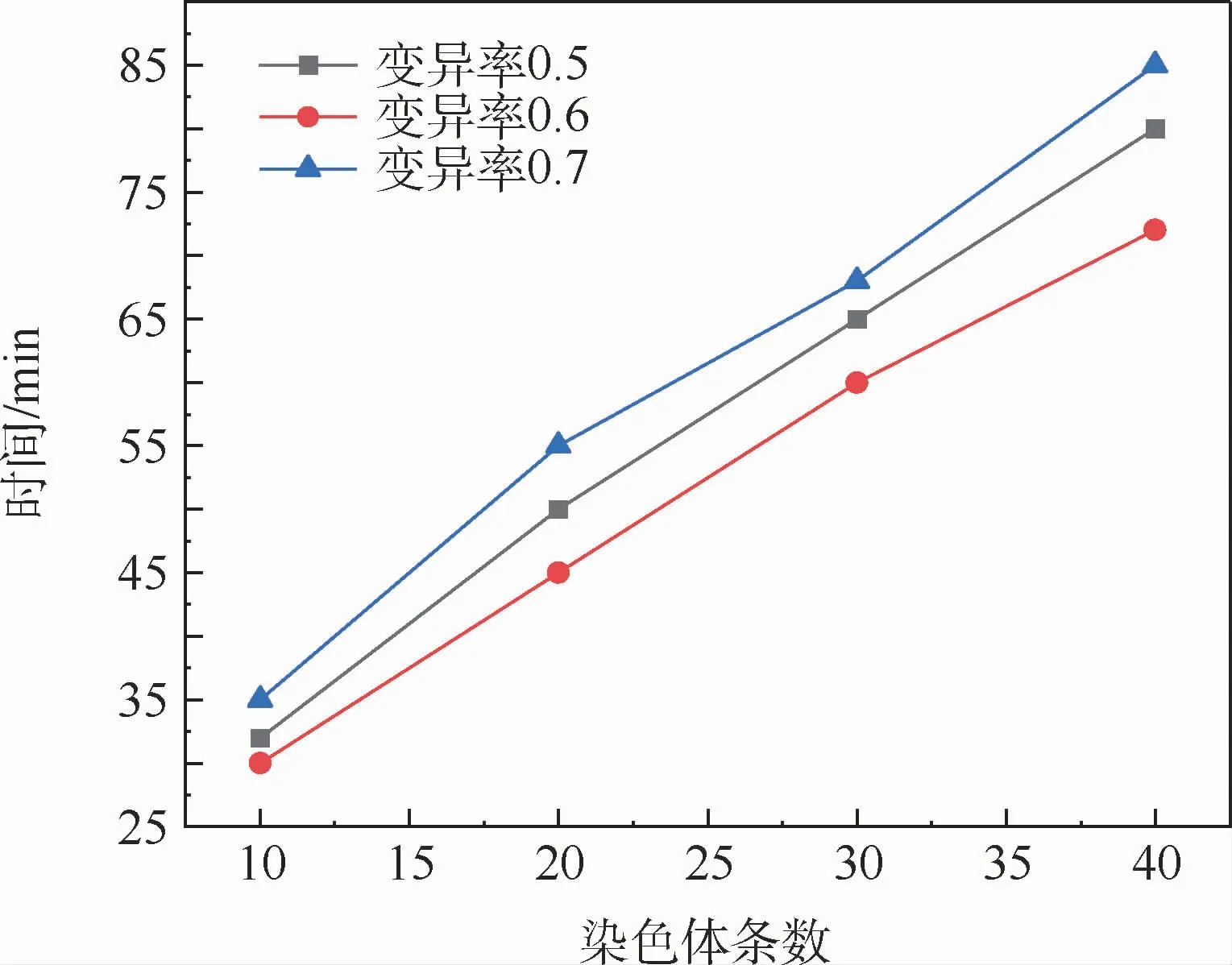
图1 不同变异率选取染色体时间折线图Fig.1 Broken line graph of chromosome selection time with differentmutation rates
5)精英比率。
当前种群中适应度最高的个体不参与交叉运算和变异运算,而是用来替换掉本代群体中经过交叉、变异等遗传操作后所产生的适应度最低的个体,本例中设置精英比率为0.08。
6)停止准则。
遗传算法在实际操作中都要经过多代进化,直到适应值趋于稳定,或者找到最优解或者达到规定的遗传代数,进化过程结束。本文的样本集精简目标是在不降低代码覆盖的前提下尽可能降低测试用例的数量。当算法执行到特定迭代次数或选择出的测试用例不再发生变化时,算法停止。
4 实验设置与评估
4.1 实验准备
1)实验环境。实验在W indows 10系统下,配置为Intel Core i7-4790 CPU 3.6 GHz,8 GB内存,使用peach等工具采用启发式遗传算法对模糊测试样本集进行精简优化。
2)测试环境与目标程序。在模糊测试实验中,本文选取peach[14]作为模糊测试工具:①安装方便;②有开放的使用说明;③不同的命令可实现多种操作,在获取样本的执行路径时无需再借助于其他工具。同时选取 mspaint、pdfium、VLC Player作为目标程序。
3)数据来源。本文实验所需的jpg、PDF、AVI类型数据来源于互联网开源数据集。此数据集中包括很多重复数据,并且不同数据之间存在交叉;其将增加模糊测试样本集录入的时间,并使peach在变异时产生更多重复甚至没有任何利用价值的测试用例。
4.2 实验方法与分析
3.3节阐述了本文方案的算法评价指标,通过时间复杂函数来展现算法随着初始数据的变化而变化的程度,而这些表现可以多种角度来展示。为了更直观地展现算法的有效性,设计了以下实验,并以jpg类型数据实验过程进行分析。
1)样本集数量。
启发式遗传算法在0-1矩阵的基础上操作,将矩阵中的元素“1”看作是遗传算法中的染色体。在遗传算法过程中,通过父代染色体的变异和交叉产生新的染色体,父代的选择也是样本精简的一个过程,只选择性能好的染色体作为父代,直至进化到停止准则要求时间。实验中,对初始样本集做了定向的选择。jpg1:随机选择;jpg2:3组jpg1;jpg3:随机选择,jpg4:随机选择。精简样本集的数量与初始样本集的数量关系在表1中给出。由前2组数据可以看出,第2组数据在启发式遗传算法后数量明显减少,jpg2包含3组jpg1,jpg2的精简样本集数量与第1组一样,启发式遗传算法在某种程上可以对样本进行精简,但是jpg2是特殊的数据组,不能体现算法的实用性。jpg3随机选取的2 000个样本集和jpg4随机选择的4 000个样本集,其经过启发式遗传算法优化后获得相应精简样本集,即启发式遗传算法并不会受选取样本的影响。从jpg2和jpg3两组数据可以看出,该启发式遗传算法可以减少样本集的数量;从jpg1、jpg3和jpg4的初始样本集数量和精简样本集的数量进行观察,假设存在精简比例,那么jpg3的精简样本集数量应该是818,jpg4的精简样本集数量应该是1 636,而实际精简样本集数量却比期望低。这是因为:选取样本集数越大,该样本集所包含“基因”越多,其可覆盖“染色体”就越多,剩余不能覆盖的“染色体”就越少,那么精简样本集数量就越少。
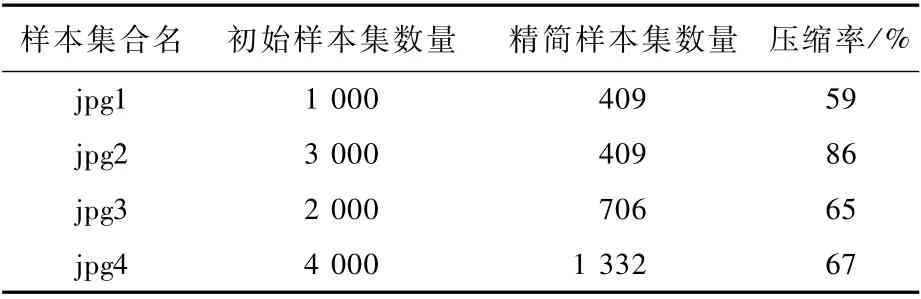
表1 样本集数量Tab le 1 Num ber of sam p le sets
2)模糊测试时间。
为了验证本文启发式遗传算法的有效性及能否提升模糊测试效率,对整体模糊测试时间进行统计。将表1中所采用的4组数据进行启发式遗传算法优化后进行模糊测试,其花费的时间如表2所示,通过模糊测试时间的变化来说明该启发式遗传算法是否可以提升模糊测试效率。样本数量与测试用例个数的对比情况如图2所示。在一定程度上,测试用例的产生主要取决于原始样本的最小样本集合。模糊测试时间与样本数量情况如图3所示。精简后的样本模糊测试时间低于未精简样本的模糊测试时间;样本集精简后模糊测试的时间比精简前降低了22%。本质上,模糊测试用例的数量由输入样本集的数量来决定,而模糊测试用例通过启发式遗传算法去除冗余可以提升模糊测试的效率。
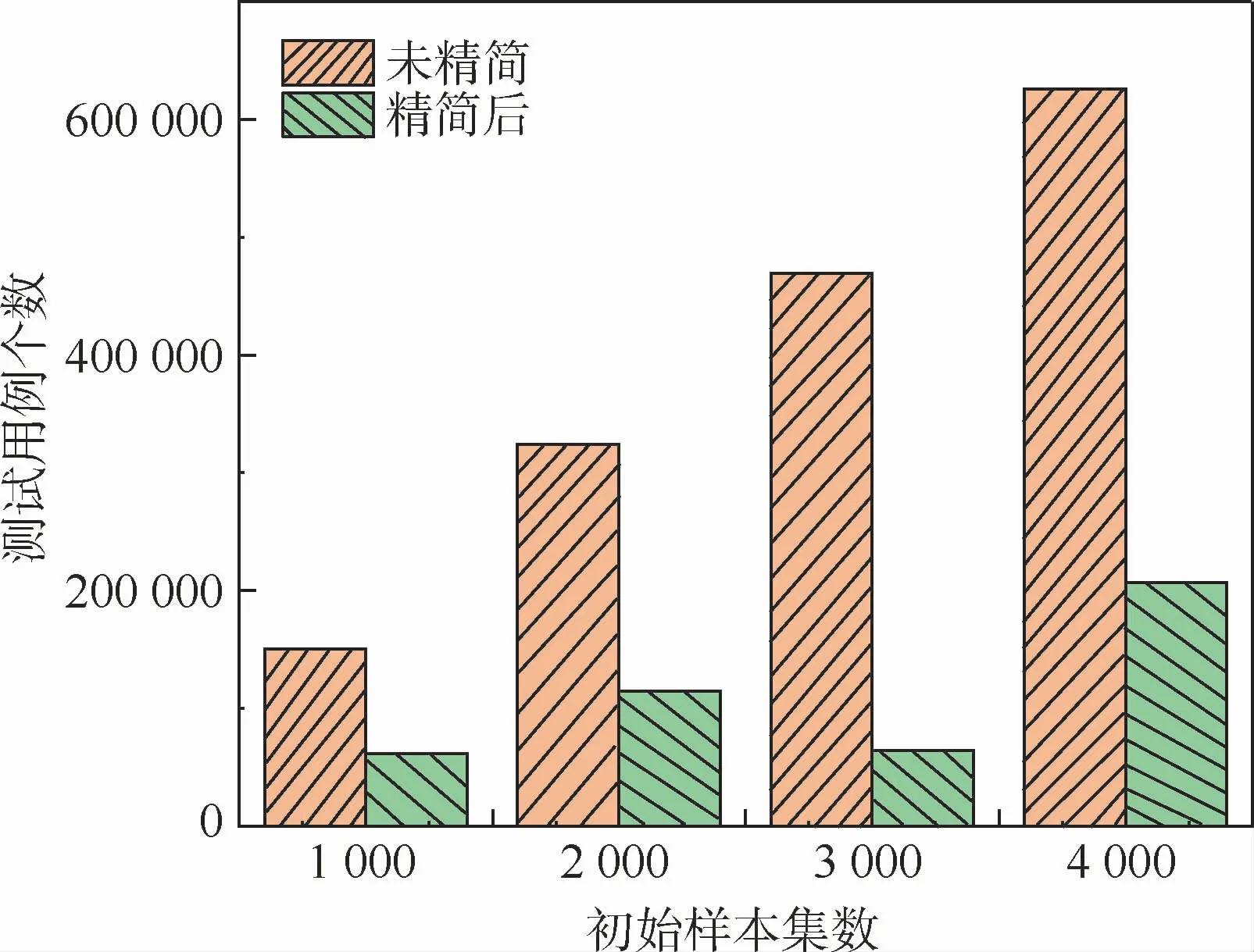
图2 测试用例个数与样本数量Fig.2 Number of test cases and number of samp les
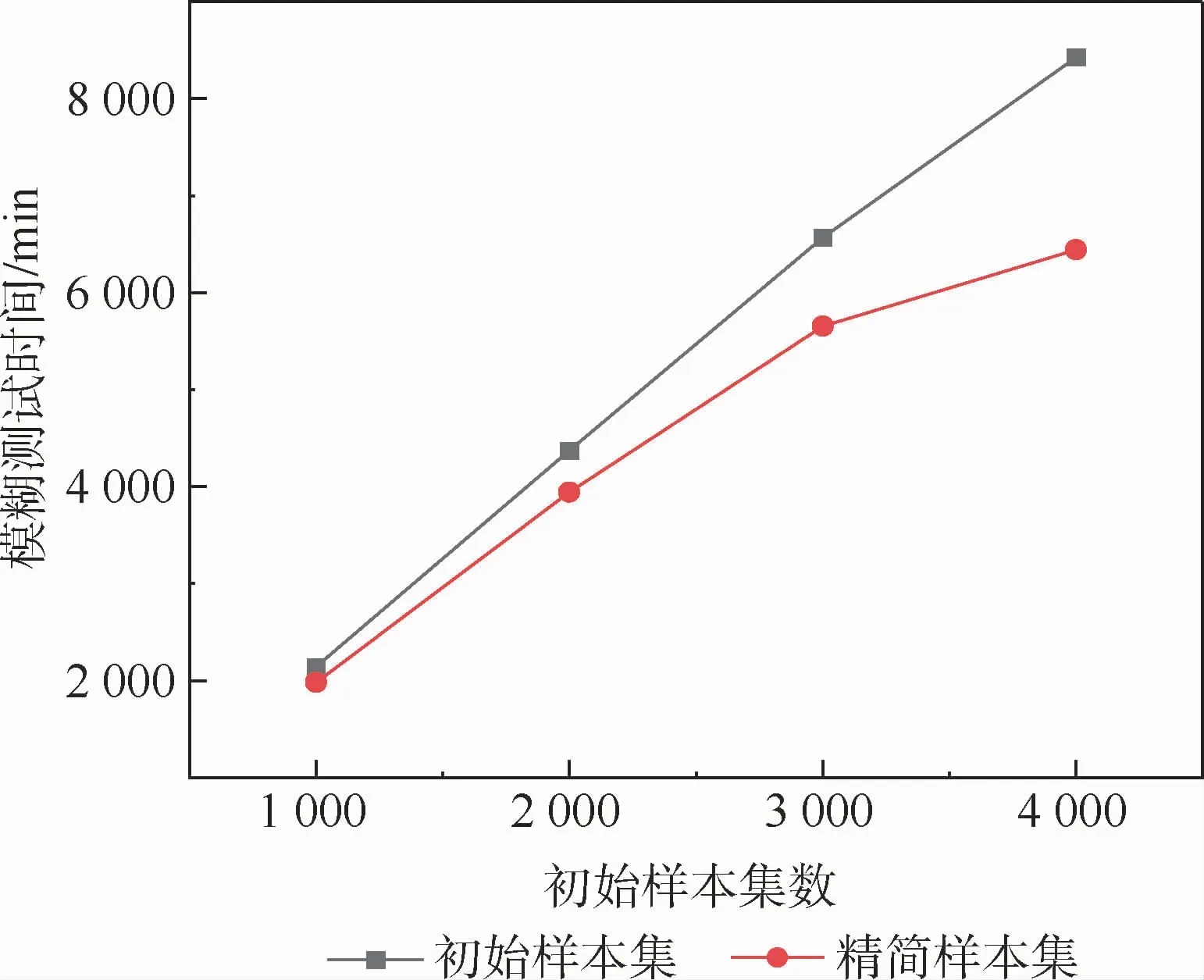
图3 模糊测试时间与样本数量Fig.3 Fuzzy testing time and sample size
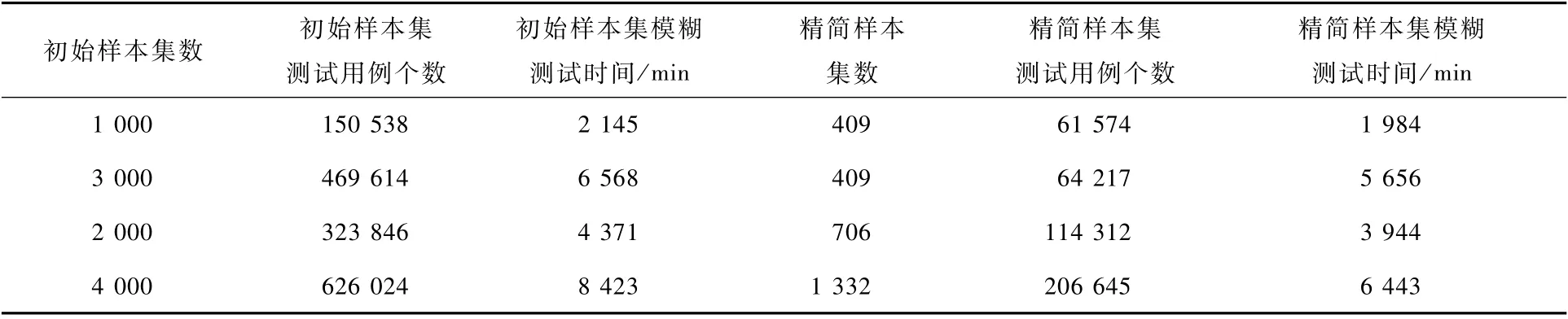
表2 模糊测试时间Tab le 2 Fuzzy testing tim e
3)样本质量。
每个样本都有对应的代码块,根据不同的代码块变异而产生测试用例。在未精简时,重复样本产生无用测试用例。在时间一定的前提下,输入同一组初始种群,对产生的测试用例进行标记以保证获取的测试用例的不重复性,统计精简前后变异产生的测试用例的数量。本文从jpg3和jpg4中各取一个子集,名为Test1和Test2。实验测试用例数据情况如表3所示。测试时间一定时,未精简的样本集短时间内产生的测试用例大于精简后的样本集所产生的测试用例,但其标记后的测试用例个数小于精简后的标记个数。样本集在经过启发式遗传算法后,其样本的质量有所提升;在相同的时间内,其产生的测试用例存在的重复性小,同时精简前后的代码覆盖率没有发生变化,算法兼顾了样本质量。

表3 测试用例数据Tab le 3 Test case data
4)对比实验。
通过比较文献[3,15]提出的算法,观察不同模糊测试样本集优化方案的处理效果。文献[3,15]对比实验按照文献原文中设定参数进行精简优化,对千兆级样本数据进行处理,实验数据如表4所示。通过表4可以观察出,使用文献[3,15]和本文所述样本集精简方案对初始样本集进行优化后,样本集中数量有一定下降,且代码覆盖率都维持在初始样本水平,保证了样本质量。但进一步观察,结合图4所示,贪心逼近算法运算速度较快,但需多次迭代方能达到和其他算法相同的精简数量,因此其速度却远远要慢于启发式遗传算法的速度;并且如表4所示,本文所述方案处理过的样本集中数量少于文献[3,15]提出的方案,说明经过本文所述方案优化后的样本集更加有效。
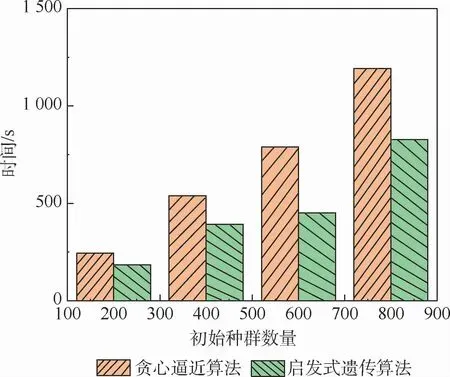
图4 不同算法产生相同精简样本集所需时间对比Fig.4 Comparison of time required for different algorithms to produce the same simplified sample set

表4 多种方案测试样本数量和覆盖率Table 4 Test sam p le size and coverage rate for m ultip le schem es
5 结 论
1)启发式遗传算法在遗传算法上进行改进并且应用到集合覆盖问题中,通过染色体来表示集合中的覆盖情况,以高质量的染色体为背景,对染色体进行启发式改进,使之在种群中随时进化,从而精简优化样本集。该方案比传统方案压缩率提升约40%,展示了该算法的有效性。
2)本文在进行优质染色体选择过程中使用0-1矩阵与集合覆盖的方式来完成优质染色体的选取工作,并且改进了基因交叉的规则,加快模糊测试速度,同时能够兼顾样本质量和处理时间,测试时间降低了约22%,比传统方式更加高效。
