基于能源分解的用户用电行为模式分析
2022-03-08卢瑞瑞于海阳杨震赖英旭杨石松周明
卢瑞瑞,于海阳,杨震,赖英旭,杨石松,周明
(北京工业大学 信息学部,北京 100124)
近年来,大数据技术给人们的生活带来了很多便利,而智能电网被看作是大数据技术的应用之一,吸引了很多学者利用用户数据挖掘数据中潜在价值方面的研究。
能源问题是当今社会面临的最大挑战之一。在美国,建筑消耗的能源占总能耗的40%,其中73%是电力消耗[1]。研究表明,有效的能源管理可以减少建筑物的10% ~15%电力消耗[2],用户对家用电器用电量的掌握有助于调节用电行为,实现能源优化调度。而能源分解可以获得用户的详细用电信息,让用户对自己的用电状态更加了解,在一定程度上也可以诱导用户用电行为达到节能的目的。另外,能源分解后的数据可以反映详细的能源使用情况,给用户提供改进的依据。详细的能源分解可以实现对家庭用户电力消费行为分析,实现配电的双向交互、信息交换、信息处理等环节的智能控制,提高供电侧的可靠性和安全性,从而实现用户方和供电方的利益最大化。
由于智能电网是直接面向用户的,网络结构复杂、类型繁多,如何深入分析用户的用电行为,挖掘出用户用电行为潜在价值,成为该领域的研究重点和难点。20世纪80年代,麻省理工学院提出了非侵入式负载监测(NILM)[3]方法,该方法首次从智能电表端采集用户的聚合用电信号并从中推断出每个电器的用电信号。随后,研究人员在这些方法的基础上寻找更有效的电信号特征,如稳态功率的谐波、电流消耗和瞬态噪声[4-7],这些方法都称为基于事件的方法,其依赖于通过捕获特征来识别设备[8];另外一种方法不依赖于事件检测分类设备,而是综合考虑所有的样本建立预测模型,是基于非事件的方法。2010年,Kolter等[9]使用稀疏编码算法来学习每个设备在一周内的功耗模型,再结合这些学习模型,仅使用其聚合信号来预测以前未知家庭中不同设备的功耗。Kim[10]和Parson[11]等 使 用 因 子 马 尔 可夫模型(FHMM)将用户的聚合用电信号分解成单个电器的用电信号,并且隐藏设备的状态。2012年,Kolter和Jaakkola[12]在FHMM框架的基础上,提出了基于凸规划的近似算法。随着深度学习的发展,一些研究人员提出使用深度神经网络的方法通过分类来识别设备从而进行能源分解[13-15]。除了这些单通道源分离工作外,研究人员还致力于利用其他信息来进行能量分解。2016年,Batra等[16]提出了单个设备的功耗可以通过具有相似特征家庭的数据估计得出。然而,所有这些技术大部分都需要高分辨率的数据,而大多数智能仪表的采样率都达不到这个要求。另外,这些方法需要复杂且耗时的分解过程,难以在普通家庭中快速投入使用。
2005年,李培强等[17]基于模糊聚类原理提出了模糊C均值算法和模糊等价关系2种算法对变电站的综合负荷进行分类的方法。2009年,王璨和冯勤超[18]提出从当前的市场价值、潜在市场价值和区域贡献价值等角度来对用户的用电行为进行聚类研究。这2种聚类角度都过于宏观,未考虑到用户的用电负荷特征,不能实现用户电力负荷的精细化管理。2010年,李欣然等[19]提出使用模糊C均值算法对用户的日用电负荷曲线进行分析来对用户所属的行业进行分类。2018年,Zhong等[20]提出使用K-Means算法对用户添加标签,实现用户画像为电力公司了解用户的电力消耗习惯、了解用户需求、提高服务质量提供数据支撑。2019年,Nordahl等[21]提出使用K-Medoide方法来分析和理解家庭的用电量数据,通过提取的知识为每个特定家庭创建正常用电行为模型用于异常行为检测。
综上分析,在众多的能源分解方法中,稀疏编码方法相对简单有效,根据相似用户预测能耗的方法有一定的合理性但是不完全据此预测,而智能电网用户用电行为分析方法仍过于粗糙,需要进一步精细化分析。如何提高能源分解的准确性,并合理利用分解结果对用户的用电行为进行分析是一个有趣且充满挑战的问题。
本文针对现有能源分解系统分解准确率不高、难以应用到普通用户、用户用电行为聚类分析特征欠缺等问题,首先,提出基于稀疏约束的能源分解方法,在不丢失信号特征的前提下更简单地获取信号中蕴含的主要信息,同时也方便对信号做进一步的加工处理。其次,提出基于同质性约束的能源分解方法,在能源分解的过程中把用户之间同质性考虑进去,来提高分解系统的准确性。最后,通过对基于用电模式的用户行为聚类分析,完成智能电网用户的分类,并分析每类用户的用电特点。
1 系统描述
1.1 系统架构流程
本文的整体结构可以表述为如图1所示的四元结构图,普通用户家庭、智能电网、数据分解系统和聚类分析系统是整个结构的4个组成部分。普通用户家庭从智能电网获取电能,从数据分解系统获取一段时间内的用电反馈。智能电网给用户提供电能,并采集用户的用电数据反馈给数据分解系统和聚类分析系统。数据分解系统将总用电数据分解成单类用电器的用电数据反馈给用户,或者提供给聚类分析系统分析用户的用电行为。聚类分析系统通过数据分解系统提供用户的详细用电数据对用户用电行为进行聚类分析应用于网络规划、需求响应和信息推荐等。
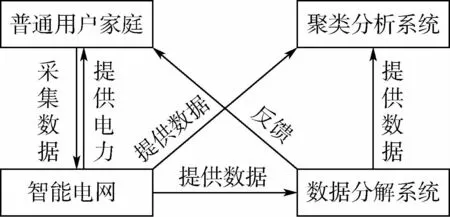
图1 系统四元结构Fig.1 System quaternion structure
系统首先从智能电网采集数据集,对数据集进行筛选和预处理,选择用电数据多的用户,统一数据格式,把数据处理成结构化的矩阵数据为使用做准备;其次能源分解模块把用户单类电器用电数据作为训练集训练模型,用户总的用电数据作为测试集,把用户总的用电数据分解成单类用电器的用电数据输出;然后评测能源分解模块的性能,能源分解模块分解出来的单类用电器的用电数据也可以提供给其他第三方应用;最后使用能源分解前的总用电数据和能源分解后的单类电器用电数据对用户进行聚类,并对比分析其聚类结果。
1.2 系统主要模块
1.2.1 数据预处理模块
本文采用Pecanstreet数据集进行实验,该数据集中包含69个电器,每个用户的单类用电器是每小时采集一次用电量,如果采集500个家庭一个月的用电量可达到2亿多条数据。数据规模庞大,用户用电器类别不一致,并且包含很多无效的数据。因此,本文对原始数据集进行预处理。首先,筛选可用的数据,选择部分用电器和用户的用电数据进行研究;其次,处理缺失数据,对邻近时间段的数据求均值进行插入来完善数据集;再次,处理异常数据,把长时超出电器负荷的值作为异常数据,用邻近时间段的数据来替代;最后,把数据转换成本文需要的数据格式为实验做准备。其中,数据筛选部分选取数据的准则为:对于电器类别,选择大部分家庭中都有的用电器作为主要研究对象,不常见或者只存在部分家庭中的用电器的用电数据对其求和作为杂类;对于用户,选择用电数据较多的用户,丢弃连续多天不用电或用电异常的用户。最终得到5类电器(空调、电炉、洗衣机、冰箱和其他电器)的总和,264个用户2周内的用电数据用于本文的实验。
1.2.2 能源分解模块
本文的能源分解模块把用户的总用电数据分解成单类用电器的用电数据。非负矩阵分解(nonnegative matrix factorization,NMF)是处理盲源分离问题的一种有效方法,其可以通过一些线性组合来近似混合信号。2010年,Kolter等[9]提出判别式稀疏编码的能源分解方法,认为用电数据存在稀疏性,在用非负矩阵进行能源分解时,优化目标中加入了L1正则化项来进行稀疏约束。本文基于稀疏非负矩阵分解这个研究方向来改进原有的算法,提升能源分解的准确率。首先,收集数据并对数据预处理,把数据稀疏表示,生成稀疏约束正则项L1;其次,计算不同家庭特征和用电量之间的相关性进行相关性分析,建立同质性正则项L2;然后,基于非负矩阵分解算法、同质性约束和稀疏约束建立模型;最后,继续优化模型并进行模型求解。
1.2.3 聚类分析模块
本文的聚类分析模块利用能源分解模块得到的分解结果对用户的用电行为进行聚类分析。首先,总结了传统的智能电网用户聚类方法,然后,选择基于K-Means聚类算法的智能电网用户聚类方法对其改进应用于本文提出的方法。
2 能源分解和聚类分析设计
2.1 基于L 1/2范数和同质性约束的能源分解方法
2.1.1 基于非负矩阵分解的能源分解模型
NMF是由Lee和Seung[22]于1999年在Nature上提出的一种矩阵分解方法[23],该方法分解后的所有分量都是非负的,并且可以实现降维的目的。具体地,NMF方法主要解决如下问题:给定非负矩阵X,找到非负矩阵B和A使得X≈BA,目标函数可以建模为

式中:X为待分解矩阵;B为特征矩阵,每一列是一个基向量即特征,矩阵A是代表特征重要程度的权重矩阵,即A的行表示每个基向量的贡献大小。优化式(1),找到最优的B和A使得式(1)最小。式(1)在求解时,如果只考虑B或者A一个变量时是凸函数,但是同时考虑2个变量时就是非凸问题,对于非凸函数想要找到全局最优解是不切实际的。Lee和Seung[22]提出使用乘性迭代法进行求解,对2个变量交替迭代寻找最优,迭代如下:

对于NMF方法进行优化求解时,是一个非凸优化问题,最终得到的是一个局部最优解,也就是说基本NMF方法的最优解不唯一。因此,在实际应用中,研究者通常会加入一些数据的先验知识,缩小解的范围并且使求解结果更加合理。而这些先验知识则是通过给NMF添加正则项约束的方法加入,添加正则化后的NMF方法模型如式(4)所示:
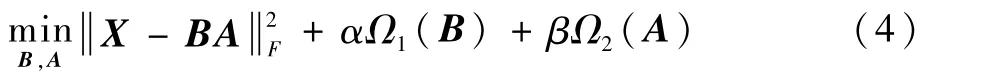
式中:函数Ω1和函数Ω2表示正则化项,对矩阵B和矩阵A进行约束;α和β为正则项系数,来控制该正则项约束的强弱。正则化的NMF方法因其加入了先验知识,使矩阵分解的结果具有了一定的实际意义,更具有可解释性,因此越来越受到关注。本文提出的能源分解方法即建立在正则化的NMF方法基础之上。



式中:L为损失函数用来描述真实值与预测值之间的误差;Ω为正则项。正则项可以把先验知识加入到模型的学习中去,让学习到的模型具有指定的特性,让经验风险和模型复杂度同时最小。正则化还可以缩小解的范围,加快模型的求解速度,常见的正则项有L2范数、L1范数、L0范数等。其中L2范数可以防止模型过拟合,L1范数和L0范数正则项对参数惩罚可使参数稀疏。
L0范数、L1范数和L2范数的定义如下:
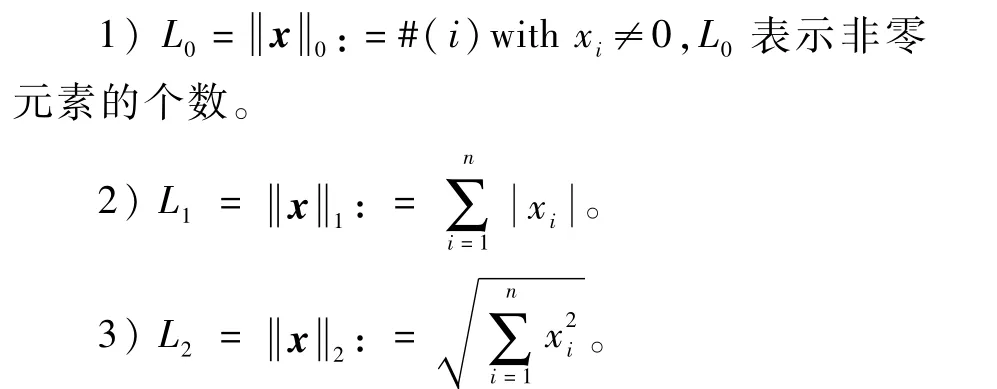
范数表示的是某个向量空间或者矩阵中每个向量的长度或者大小。因此,范数正则项可以理解为对模型参数解空间添加限制,L2范数把参数的解限制在一个圆形的球体内,L1范数把参数的解限制在锥形体内,L0范数则把参数的解限制在坐标轴上。L2范数正则项使模型的解取圆内的参数,缩小解的范围以防止模型过拟合,提升模型的泛化能力。而L1范数与L2范数不同之处在于L1范数把解约束在锥形体内,等直线最先和解空间相交的地方总是在锥角即坐标轴上,而坐标轴上的点其他维坐标是零。因此,L1范数正则项使解中出现零更多,从而达到稀疏约束的目的。
近年来,对L1正则化性能的研究已经取得了很大的突破,然而,在实际应用中L1正则化产生的性能往往小于L0正则化,但是对L0正则化的求解又是一个NP难问题。本文通过对范数正则项的分析提出L1/2范数正则项来解决L1范数稀疏约束效果不好,L0范数不易求解的问题。基于L1/2范数稀疏约束的非负矩阵分解能源分解目标函数定义为
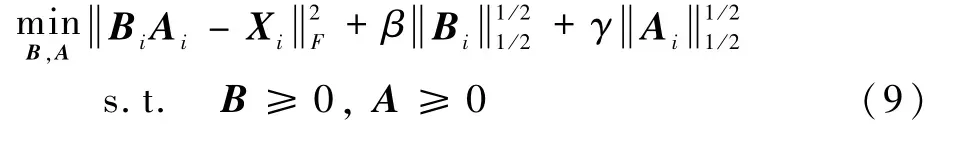
式中:Xi为第i类用电器的用电数据矩阵,i=1,2,3,4,5分别为空调、洗衣机、电炉、冰箱和其他电器的总和;Bi为特征矩阵;Ai为特征重要程度的权重矩阵;β、γ为L1/2范数正则项的系数,用来控制正则项的强弱。对于L1/2正则项定义如下:
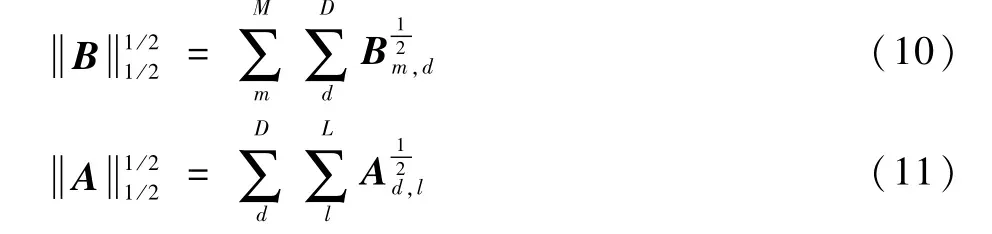
式(10)和式(11)可以通过如下所示的乘性迭代来求解:
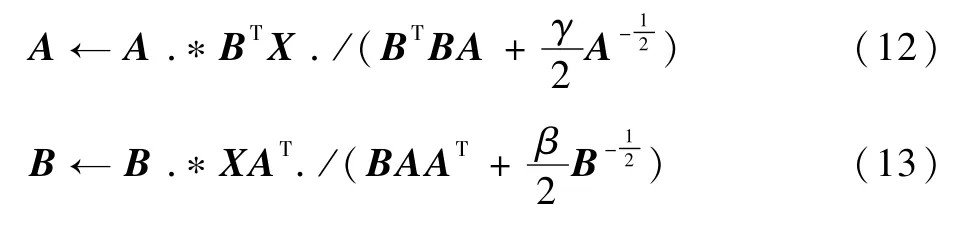
式中:符号“.*”和“./”表示矩阵的点乘和点除。如果矩阵A或者矩阵B中的元素为0,可以在0元素上加上一个很小的数进行平滑,避免分母为0。
2.1.3 用户用电模式同质性建模
在社交领域中,同质性表示不同用户之间的相似性[25]。本文利用家庭用电模式之间的相似性进行建模。
1)用户用电模式的相似性
利用相似的家庭相似耗能预测,可能得到错误的结论。因此,本文只考虑把相似性作为基础模型分解能源时的一个影响因素,来提高能源分解的准确率。
受此启发,本文通过对不同的数据集进行研究分析发现,总用电量和单类用电器能耗之间也存在着相似性。用电量较高且用电量比较相似的用户在对空调等大功率电器使用上具有一定程度的相似性。用电量较低且用电量比较相似的用户在对照明设备等小功率电器的使用上有着一定的相似性。同样,家庭住宅面积相似的用户在空调设备的用电上存在着相似性。
2)同质性模型
总用电量相似的家庭在空调等大功率电器的用电量更相似,家庭住宅面积相似的家庭在空调、照明设备等用电器的用电量更相似。本文利用这一先验知识,构建同质性系数,通过添加与同质性系数有关的正则项,来提高模型的分解性能。
首先,本文定义用户i和用户j之间的同质性系数为ε(i,j)并且满足:
①ε(i,j)∈[0,1]。
②ε(i,j)=ε(j,i)。
③同质性系数的值越大,用户之间的相似度就越大,即用户在某一用电器使用量上越相似。
用户在某一用电器用电量的相似性在本文提出的能源分解模型中,可以表示为非负矩阵分解后权重矩阵的相似,因为在特征矩阵确定后权重矩阵决定用户的用电量。因此,在提到用户的用电量相似和权重矩阵相似时表达的意思相同。
对于整个模型可以添加正则项式(14)来约束权重矩阵,从而提高模型的性能。
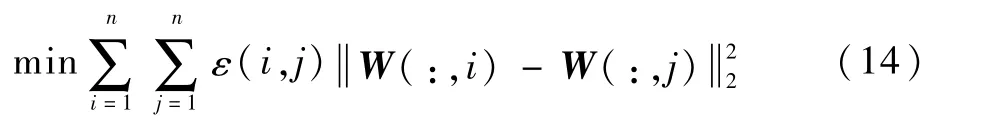
式中:W(:,i)和W(:,j)分别为矩阵W 的第i列和第j列,表示用户i和用户j对于某类特定设备的权重向量。对于2个不同的用户,某个电器的用电量越相似,在潜在空间中wi和wj的距离也会越近,同时调节它们之间的相似度的同质性系数的值也会越大。
对某一用户wi,其在潜在空间中的同质性正则项可以表示为

式中:同质性系数ε(i,j)控制着用户wi和其他用户之间的关系。对式(15)进行推导,可以得到正则项Tr(WLWT),推导过程如下:

同质性系数ε(i,j)表示相似度,常用的计算相似度的方法有欧氏距离、曼哈度距离、闵可夫斯基距离、余弦距离等。本文使用余弦距离相似度公式来表示用户i和用户j之间的同质性系数,对于第k类用电器,用户i和用户j之间相似性ε(i,j)定义如下:
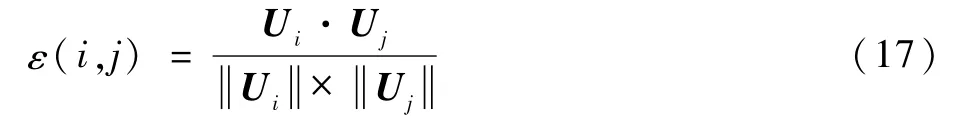
式中:Ui为用户i对第k类用电器的用电量向量。
2.1.4 基于用户用电模式相似性建模
由于同质性不能完全代表一个相似家庭的用电数据,本文只考虑把这一性质作为约束项加入基于非负矩阵分解的能源分解模型来改进基础模型,提高模型的性能。从数据出发,本文只考虑加入总用电量同质性和面积同质性。总用电量相似的家庭在单类用电器上存在着相似性,面积相似的家庭在空调的用电量上更相似。首先,计算总用电量同质性系数矩阵,对每类电器单独计算一个用户同质性系数矩阵。对于智能电网用户间的同质性系数通过用户的用电数据计算,训练数据和预测数据采用不同的计算方法。对于训练数据集,因为用户的单类用电数据是已知的,很容易通过余弦相似度公式得到同质性系数矩阵。而对于测试数据集,单类电器的用电量是未知的,此时采用近似计算方法来计算待预测家庭中每类电器的同质性系数,在训练数据集中找到总用电量最接近的3个用户,取这3个用户对应电器同质性系数的均值来计算。然后,计算面积同质性系数矩阵。对于面积同质性系数,采用相同的计算方法。最后,针对不同类型的电器,本文通过一个系数矩阵来控制同质性正则项的强弱。最终生成基于同质性约束的非负矩阵分解能源分解模型如下:

2.1.5 能源分解方法建模
在本节中,将提出本文最终的能源分解方法,再进一步优化,并给出求解过程。
1)基于L1/2范数稀疏约束和同质性约束的能源分解方法,建立的能源分解训练模型如下:
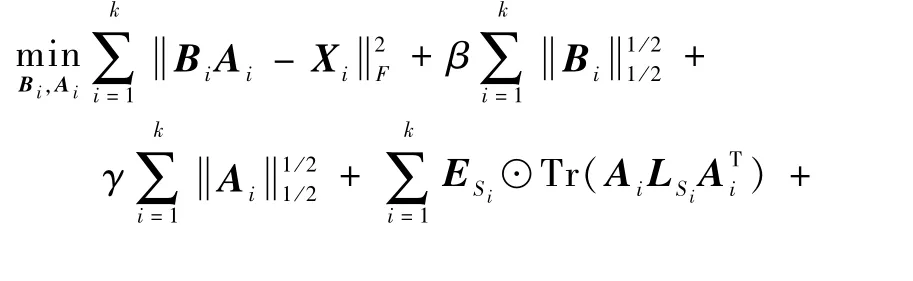

对于训练数据集,使用目标函数式(19)求解得到每类电器最优的特征矩阵Bi。对于测试集,用式(20)为每类电器找到最优的权重矩阵Ai,最终用式(21)预测每类电器的用电量。
2)模型优化与求解。如果训练过程和分解的过程能够同步进行,那么在求解过程中这2个结果会相互影响,对预测结果会有正向促进作用。因此,本文继续改进模型得到最终能源分解模型如下:

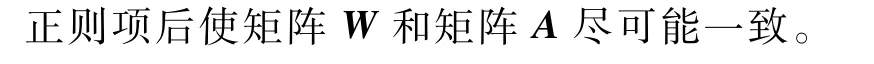
在上述内容中,已经得到了本文提出的最终的能源分解模型,如式(22)所示,但是该公式无法直接给出W、B、A的解,本文将采用乘性迭代法交替更新W、B、A来找到其最优解,具体过程本文不再赘述,迭代规则如下:

2.2 基于能源分解的用户用电行为聚类分析方法
2.2.1 基于改进K-Means聚类算法的用户聚类模型
选择K-Means聚类算法来辅助验证本文提出的观点。首先,介绍传统的基于用电行为的KMeans聚类算法。
假设数据集I={x1,x2,…,xn}∈RT,xn是T维的向量,表示用户n在T段时间内的总用电量,具体算法描述如下:
步骤1 随机初始化k个聚类中心u1,u2,…,uk∈RT。
步骤2 针对每个样本点,计算其与每一个类中心的距离,离哪个类中心近就划分到哪个类中,这样完成一次聚类。
步骤3 用类均值更新聚类中心。
步骤4 判断新计算出的类中心和原来的类中心之间的距离是否小于设定的阈值(表示重新计算的类中心位置变化不大,趋于稳定),如果小于阈值,算法终止,否则返回步骤2。K-Means聚类算法中通常选择欧氏距离来计算点到类中心的距离,对于样本点到类中心的距离计算如下:
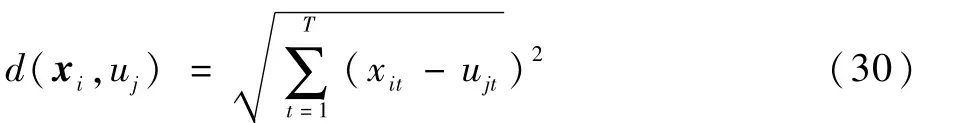
式中:xit为用户i在t时刻的用电量;ujt为聚类中心j在t时刻的数据。
为了避免总用电特征对用户聚类结果不够准确及不能反映用户的详细用电行为的问题。本文提出用能源分解后的单类用电器的用电特征来代替总用电特征,计算用户间的距离提升聚类效果,改进传统的K-Means聚类算法。
具体地,对于一个用户i,传统的方法是用一个向量来表示,该向量中的值是用户的总用电特征,现在我们用一个矩阵来表示用户i,矩阵中每一列是一个单独用电器的用电向量,K列就有K个用电器。在计算距离之前用Z-Score消除不同类电器量级不同带来的影响,改进后的算法的距离计算为
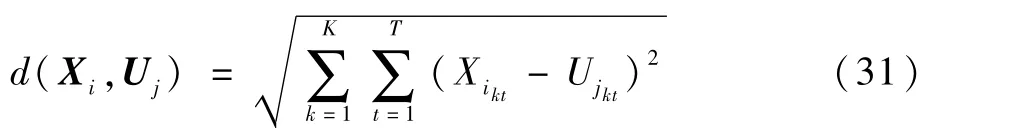
式中:Xi为用户i的特征矩阵;Uj为聚类中心j的特征矩阵;Xikt为用户i用电器k在t时刻的用电量;Ujkt为聚类中心j对于用电器K在t时刻的类中心数据。
2.2.2 初始聚类中心和K值的选择
K-Means聚类算法的第一步也是最重要的一步,即选择聚类数目K值和选择初始聚类中心。K值决定聚类结果的数目,K值不同聚类结果也不同,聚类结果对K值的依赖性在一定程度上影响着聚类分析。而聚类中心的选择影响聚类结果的稳定性,并且容易使算法陷入局部最优解。基本的初始聚类中心的选择是随机的,会使目标结果偏离最优结果,从而陷入局部最优解。因此,合适的K值和初始聚类中心对于智能电网用户的聚类结果至关重要。
本文采用最大距离法选择初始类中心。选取的初始类中心对象之间的距离应该尽可能离得远。首先,随机选取一个样本作为第一个类中心,然后,选择与第一个类中心最远的样本作为第二个类中心,接着用同样的方法选择其他的类中心。
本文选择聚类有效性指标来计算合适的聚类数目。常用的评测指标有手肘法、轮廓系数(silhouette coefficient,SC)、戴维斯-布尔丁指数(Davies-Bouldin index,DBI)、卡林斯基-哈拉巴斯指数(Calinski-Harabaz index,CHI,也被称为方差比标准)及权变矩阵。本文选择手肘法、DBI这2种内部有效性指标来选择最优的K值。这2种指标的计算方式如下:
1)手肘法。手肘法的核心指标是误差平方和(sum of the squared errors,SSE)计算如下:
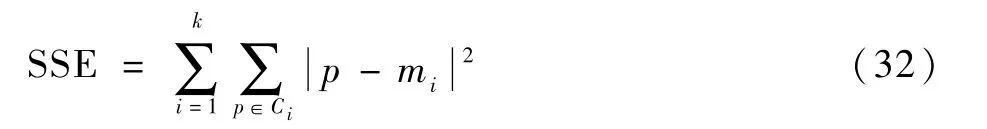
式中:Ci为第i个簇;mi为Ci的簇质心;p为Ci中的样本点;SSE为所有样本的聚类误差,代表着聚类效果的好坏。
手肘法的核心思想是:随着聚类数目K值的增多,每个簇的聚合程度也会逐渐增加,而SSE则会逐渐减小;并且当K值在小于最优聚类数目范围内增加时,SSE的下降幅度会比较大,当K值增加到最优聚类数目时,SSE的下降幅度则会骤减,然后随着K值的继续增大SSE会慢慢趋于平缓。SSE和K值的变化关系类似于手肘的形状,并且在肘部取得最优的K值,因此称为手肘法。
2)DBI。DBI有效性指标定义如下:

3 实验结果与分析
3.1 基于L 1/2范数和同质性约束的能源分解方法实验
3.1.1 不同方法对比实验结果分析
对基本的非负矩阵分解的能源分解方法(NMF)、L1范数约束的稀疏编码方法(NMF+L1)、基于L1/2正则项约束的能源分解方法(NMF+L1/2)、本文方法4种方法做实验。使用同一数据集,在参数最优的情况下经过多次重复实验,性能取均值的结果如表1和图2所示。
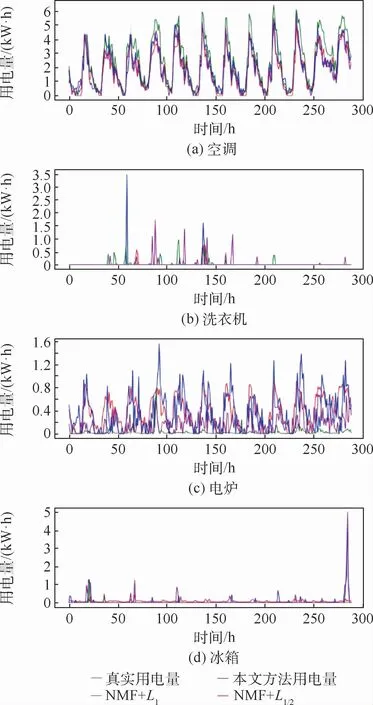
图2 真实结果和分解结果对比Fig.2 Comparison of real results and decomposition results
从表1中可以看出,在基本的非负矩阵分解模型上加入约束项之后,算法的性能都有很大的提升,并且模型的训练时间没有太大的波动。加入L1范数稀疏约束的模型相比于L1/2范数的稀疏约束的模型在训练集上效果要好,但是在测试集上没有L1/2范数的稀疏约束效果好,总体上L1/2范数的稀疏约束效果更好。本文所提出的方法,在NMF的基础上加入L1/2范数稀疏约束项、同质性约束项和一致性约束项,模型的性能在训练集和测试集上都取得了相对较好的结果。
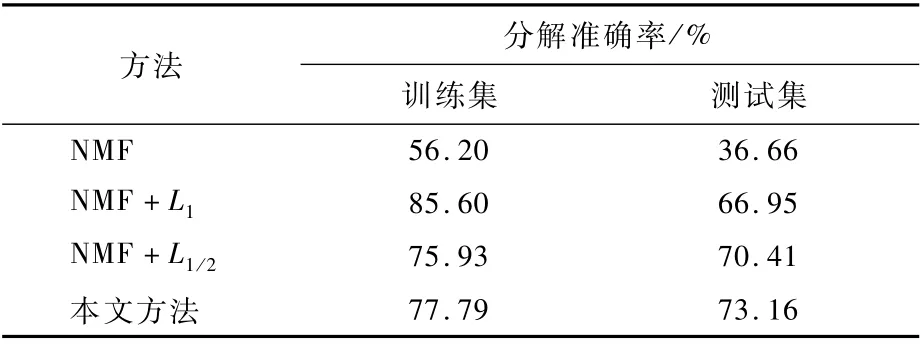
表1 实验结果Table 1 Experimental results
如图2所示,对于能源分解后空调的用电量3种对比方法都能很好的拟合,但是洗衣机、电炉、冰箱这3类电器本文提出的方法拟合效果更好。
3.1.2 同质性对实验结果的影响
1)总用电量同质性
总用电量同质性对实验结果的影响如图3所示,其中x轴为小功率电器参数El,y轴为大功率电器参数Eh,z轴表示分解准确率(Acc)。分解准确率随着参数Eh和El的变化呈现明显的规律性。参数Eh变化时对分解准确率影响较大,当参数的取值大于0.01分解性能急剧下降,当参数小于0.01时分解准确率相对稳定且较高,在0.001附近取得最优值。而分解准确率在参数El的影响下并没有呈现这种规律,参数El对分解准确率影响相对较小,随着El的增大模型的性能先增大后减小,在0.1附近取得最优值。
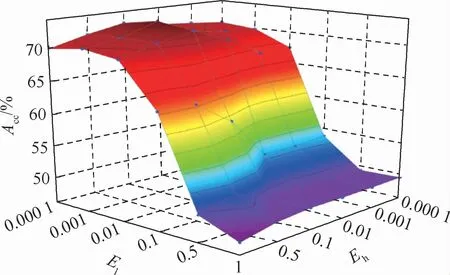
图3 不同参数对比Fig.3 Contrast diagram of different parameters
2)面积同质性
面积同质性对实验结果的影响如表2所示。可以看出,空调的同质性参数Ef取不同值时,模型的分解性能呈规律性变化,参数小于0.1时模型的性能相对较好,在0.001附近取得最优。

表2 参数E f对比结果Table 2 Par ameter E f contrast results
为了清晰地显示面积对空调分解性能的影响,随机选取一个用户分别画出空调2周内和1天内真实电量和预测电量之间的变化趋势,如图4所示,2条线变化趋势相同并且基本重合,预测值接近真实值。
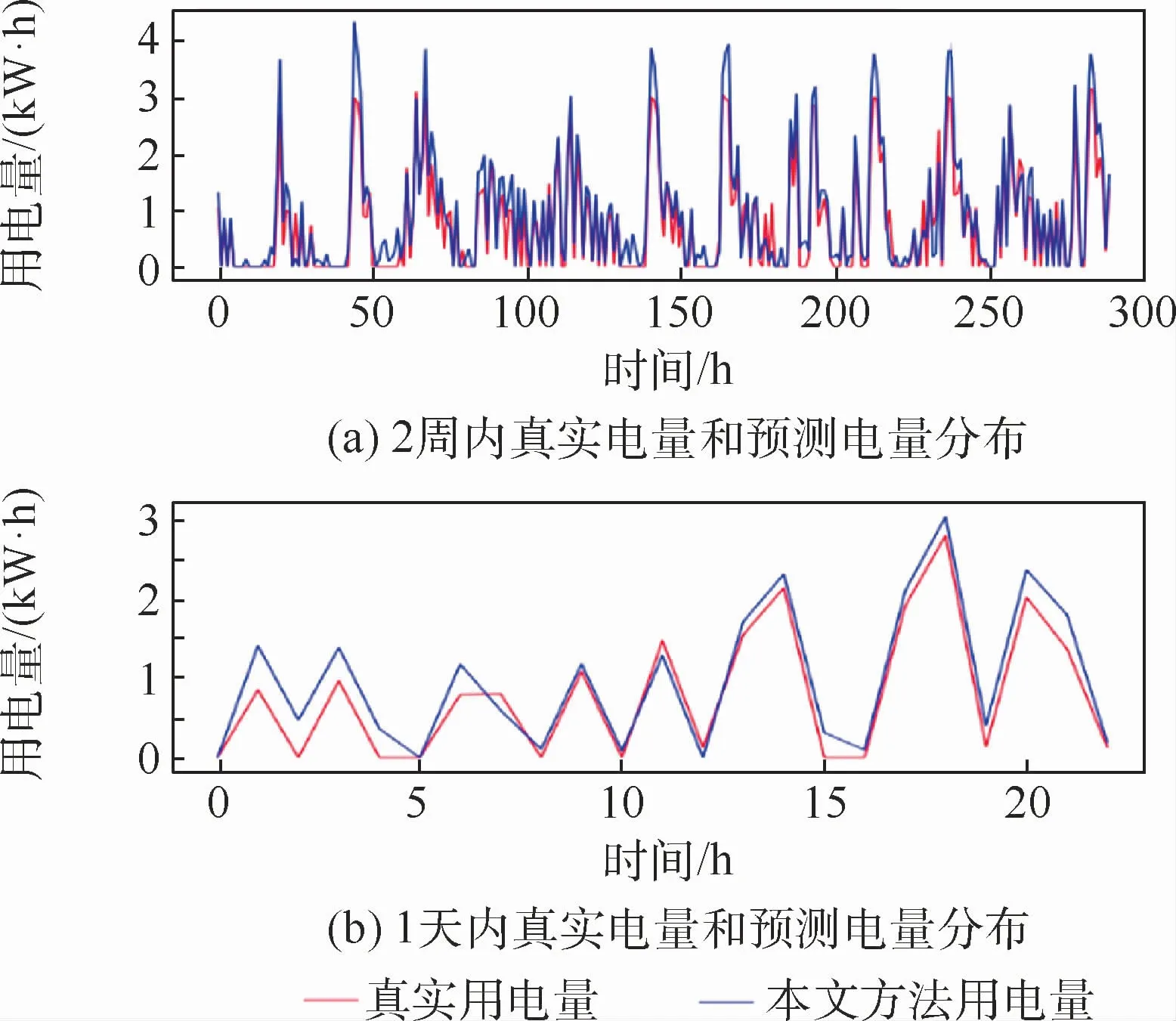
图4 2周内和1天内真实电量和预测电量分布Fig.4 Predicted distribution of real power consumption in two week and predicted distribution of real power consumption in one day
3.2 基于能源分解的用户用电行为聚类分析方法实验
3.2.1 最优聚类数目K的选择实验
1)传统的K-Means聚类算法K值确定
基于传统的K-Means聚类算法使用的是用户总用电特征进行聚类分析,即进行能源分解之前智能电表直接采集到的总用电特征数据集进行实验,采用欧氏距离计算用户之间的距离。聚类数目K取[2,10],DBI和SSE这2种有效性指标在不同聚类数目K下的结果分别如图5和图6所示,图中横轴表示聚类数目K,纵轴表示有效性指标。
从图5中可以,看出当K=4时到达SSE的变化曲线的肘部,因此在SSE有效性指标下最佳聚类数目为4。从图6中可以看出,DBI最小值为3,这表示在DBI指标下最佳聚类数目为3。但是,值得注意的是当K取4时DBI的值还非常大,而K=3或K=4时SSE差别并不大,因此本文选择K=3为传统的K-Means聚类算法的最佳聚类数目。

图5 传统的K-Means聚类算法有效性指标SSE评测结果Fig.5 Traditional K-Means clustering algorithn evaluation results of effectiveness index of traditional clustering SSE
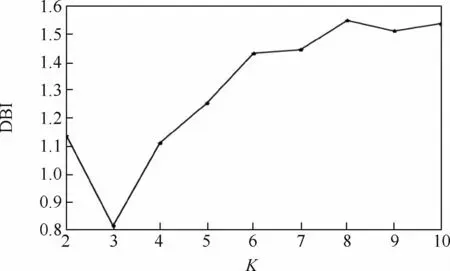
图6 传统的K-Means聚类算法有效性指标DBI评测结果Fig.6 Traditional K-Means clustering alorithm evaluation results of effectiveness index of traditional clustering DBI
2)改进的K-Means聚类算法K值确定
本文提出的聚类算法使用的是用户单类用电器的用电特征进行聚类分析的,即能源分解之后得到的数据,同样采用欧氏距离计算用户之间的距离,使用SSE和DBI这2种有效性指标选择最优的聚类数目K。随着K值的变化,SSE和DBI的变化曲线如图7和图8所示,图中横轴表示聚类数目K,纵轴表示有效性指标。
从图7中可以看出,当K=4时SSE曲线到达肘部,在SSE有效性指标下最佳聚类数目K为4。
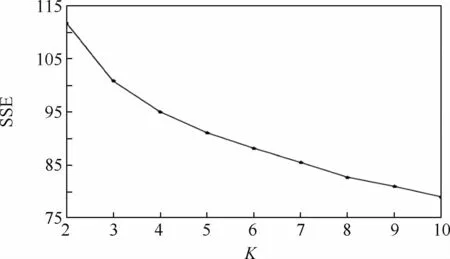
图7 改进的K-Means聚类算法有效性指标SSE评测结果Fig.7 Improved K-Means clustering algorithm evaluation result of effectiveness index of improved clustering SSE
从图8中可以看出,DBI在K=2时取得最小值,即最佳聚类数目K为2,但是在K=2时SSE还非常大,这不具有合理性。因此,本文退而求其次选择第二小DBI值处的聚类数目K,即K=4。综合分析,改进的K-Means聚类算法最佳聚类数目K应为4。

图8 改进的K-Means聚类算法有效性指标DBI评测结果Fig.8 Improved K-Means clustering algorithm evaluation result of effectiveness index of improved clustering DBI
3.2.2 不同方法对比实验
1)传统K-Means聚类算法实验分析
当K=3时,传统的K-Means聚类算法的聚类结果如图9所示,红绿蓝3条线分别代表3个类的类中心。图中:cluster0_139表示类0,clusterl_91表示类1,cluster2_34表示类2。从图中可以看出,蓝线代表的类中心变化幅度比较小,几乎趋于平稳,红线和绿线变化趋势相同,都是在5:00之后用电量慢慢上升,19:00用电量开始下降,但是变化幅度不同,绿线代表的用户变化幅度比较大,用电量比较多。对总用电数据聚类能反映用户的总体用电趋势,而每个分电器的用电特点无从得知,用电峰值也不突出,这在一定程度上会影响聚类结果的准确性。

图9 总用电量用户聚类结果Fig.9 Clustering results for users with total electricity consumption
2)改进的K-Means聚类算法实验分析
当K=4时,对用户的单独电器进行聚类算法的聚类结果如图10所示,图中每一行表示一类用户,从上到下依次为第1类、第2类、第3类、第4类用户。图10(a)~(d)分别代表4种用电器(空调、洗衣机、电炉、冰箱)的日用电特点。从图中可以看出,空调和电炉的用电趋势比较相似;洗衣机的日用电量,每个家庭使用时段不同,呈现出不同的特点;冰箱的日用电量,也可以通过电量分析,大致了解到每类用户冰箱的使用情况。实验中的4类用户中,后面3类用电都很平稳,第1类变化波动比较大并且相对用电量比较高,可能第1类用户更注重家庭饮食品质,冰箱存放食物更多。第1类和第4类用户洗衣机日用电量波动比较大,在上午和下午出现2次波峰,第2、3类用户无明显波动,这一天可能没有使用洗衣机。从图中也可以看出,第3类用户的4种用电器电量基本上没有浮动,都处于关闭状态,可以认为这类用户在这一天没有使用电器。

图10 单类用电器用户聚类结果Fig.10 Clustering result for users with single-type electrical appliances
3)对比分析
从2种对比方法的实验结果中可以看到,本文提出的聚类方法更能准确分析用户的行为,识别每类用户中单独电器的用电特点。针对每类用户的单类用电器的用电特点做出更有数据支撑、更合理的电网规划、需求响应和信息推荐等决策。由于数据集的局限本文只分析了4类电器,如果能够获得更多单类电器的用电数据,聚类结果将会有更大的应用价值。
4 结 论
随着智能电网和大数据技术的快速发展,大量用户的用电数据被记录和存储,如何合理、有效地利用这些数据挖掘出数据中潜在的价值越来越受到关注。能源分解和用户用电行为分析作为智能电网应用之一,能够用于节约能源、故障检测、电网规划、需求响应和信息推荐等。因此,对用户的电能分解并对其用电行为进行聚类分析具有重要价值,而如何提高能源分解的准确率和用户用电行为聚类效果变得极为重要。基于此,本文提出了一种基于能源分解的用户用电行为模式分析方法。采用非负矩阵分解的能源分解方法(NMF)结合L1/2范数的稀疏约束、同质性约束项及一致性约束项方法训练数据,得到的模型在训练集和测试集上都具有很好的效果,克服了传统采用NMF+L1方法得到的模型在测试集上效果不好的问题及克服了采用NMF+L1/2方法精度不高的问题。本文在传统方法NMF+L1/2上加入同质性约束项及一致性约束项训练的模型,一定程度上提高了模型在训练集和测试集上的性能。
