森林采伐机动臂时变可靠性分析
2022-03-07何昌明邓旻涯
何昌明 邓旻涯
(中南林业科技大学材料科学与工程学院,湖南 长沙 410004)
引言
第九次全国森林资源清查结果显示,截至2019年,我国森林资源总量继续位居世界前列,全国森林面积22044.62万hm2,森林覆盖率22.96%。因此,对我国现有的大面积森林的抚育、采伐、造材等作业机械化、高效化就成为一个核心的焦点。森林采伐机是一种集伐木打枝、造材、截梢、归楞、装车多功能于一体,适合于多种林地的多功能采伐机械。这种林业机械适用性非常广,能够大幅度提高木材生产率。在森林作业中,林木森林采伐机能显示出无法比拟的先进性[1]。与此同时,确保森林采伐机在工作过程中能够安全运行显得尤为重要,因为其意外事故不仅会带来巨大的经济损失,更为严重的是导致人员伤亡,对工程进度和林地的危害也不断增大。近年来,森林采伐机由于各种原因,如臂架设计时许用强度、刚度余量不大,或者是没有考虑服役期时间累积效应对结构抗力的影响等,发生的事故逐年上升。其中动臂作为森林采伐机的主要承载部件,决定了森林采伐机的作业范围和作业对象标准,影响着森林采伐机整机的作业性能,其安全性决定了整机的安全性。因此,研究林业工程领域内森林采伐机的可靠性有着非常重要的现实意义和经济意义。
1 结构时变可靠度
结构可靠度指的是在规定的时间和条件下,工程结构完成预定功能的概率,是工程结构可靠性的概率度量。而在随时间变化的过程中,工程结构能表现出腐蚀、疲劳、老化等特性,工程结构的可靠性则表现出时变特性,从而提出了时变可靠度这个概念[2]。根据时变可靠度的定义,在时间段[0,T]内结构的失效概率Pf(T)为:
Pf(T)=P{g(X(t),Y,t)<0,∀t∈[0,T]}
(1)
式中,Pf( )为失效概率,g( )为功能函数,X(t)=(X1(t),X2(t),…,Xm(t))为m维随机过程向量,Y=(Y1,Y2,…,Yn)为n维随机向量,n为时间,T为设计基准期。
早在20世纪40年代就开始了关于时变可靠性理论的研究,一直发展到现在,许多学者做了这方面的研究,时变可靠性理论的研究也更加成熟。王光远[3]根据结构抗力和载荷效应随时间变化的特点提出了时变可靠性的概念;Breitung[4]等运用跨越率方法求出载荷随时间变化的时变可靠度;Andrieu-Renaud[5]等提出了PHI2方法用于计算跨越率而求出时变可靠度;Mejri[6]基于PHI2方法提出一种可以计算非线性系统的时变可靠度分析方法;Sudret[7]解决了时间间隔Δt对上穿率计算结果的影响的问题,提出了一种改进点PHI2方法;Hu和Du[8]基于极值分布,通过将时变可靠度问题转换为时不变问题,提出一种针对极值分布的抽样方法;姜潮等[9]通过离散含区间参数的时变功能函数将时变转化为时不变问题,提出了含有区间不确定性的结构时变可靠度分析方法;最早出现于20世纪80年代的基于大量随机抽样求取可靠度的蒙特卡洛方法(Monte Carlo Simulation,MCS)。按照之前研究中解决时变可靠度问题的分析思路,主要可以分为蒙特卡洛模拟、跨越率方法和静态转化方法。其中,蒙特卡洛模拟一般计算量较大,常用于验证新方法;跨越率方法在计算跨越率上较为复杂,并且跨越率在概念上不易于理解;而静态转换法通过将时变可靠性问题转换为传统的时不变可靠性问题,从而避免了跨越率的求解,简化了计算过程同时也在概念上易于工程人员理解。
目前,韦新鹏[10]提出了一种计算高效,易于工程人员理解的iTRPD方法,既改进的基于过程离散的时变可靠性分析方法,该方法是将时变不确定性参数进行离散,从而将一个时变可靠性的问题转换为多个传统的时不变可靠性问题进行求解。若要保证结构不失效,则由时间离散的多个时不变可靠性的功能函数都必须大于零,即可靠概率:
(2)
式中,Xi=(X1(ti),X2(ti),…,Xm(ti))为X(t)进行时间过程离散后在ti处所对应的m维随机向量。
使用传统的一次二阶矩方法对式(2)中所有的时不变功能函数进行分析即可得出关于所有时不变功能函数可靠度指标和相关系数矩阵的可靠概率函数,从而获得结构的时变可靠度:
Pr(T)=Φp(β,ρ)
(3)
式中,Φp( )为p维标准高斯分布函数;β为所有时不变功能函数的可靠度指标;ρ为相关系数矩阵。
因此,本文综合考虑森林采伐机动臂结构的时变特征,通过iTRPD方法,建立森林采伐机动臂结构的时变可靠性模型,并以工程实例为背景,求得可靠性指标和失效概率。
2 森林采伐机动臂的力学模型分析
就森林采伐机动臂结构而言,其结构会随着使用年限的增加而表现出腐蚀、疲劳、老化等特性,从而导致结构抗力的逐渐弱化。同时考虑森林采伐机动臂抗力和载荷效应2个设计参数随时间变化的可靠度理论,即对森林采伐机动臂的时变可靠性分析[11,12]。因此,动臂结构的时变可靠性模型:
G(t)=R(t)-S(t)
(4)
式中,G(t)为动臂结构的极限状态函数;R(t)为抗力的时变函数;S(t)为载荷效应的时变函数。
即动臂结构的失效概率表示为:
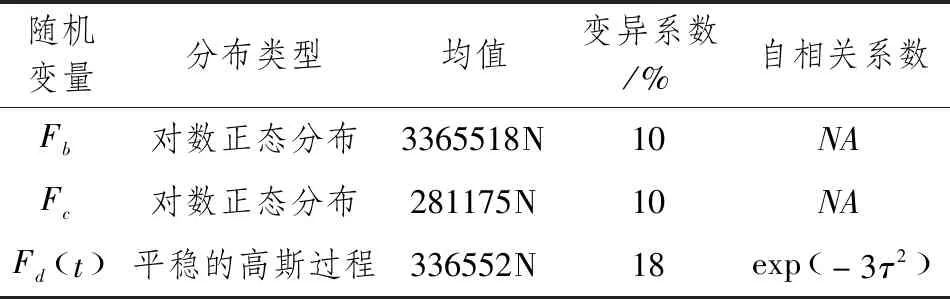
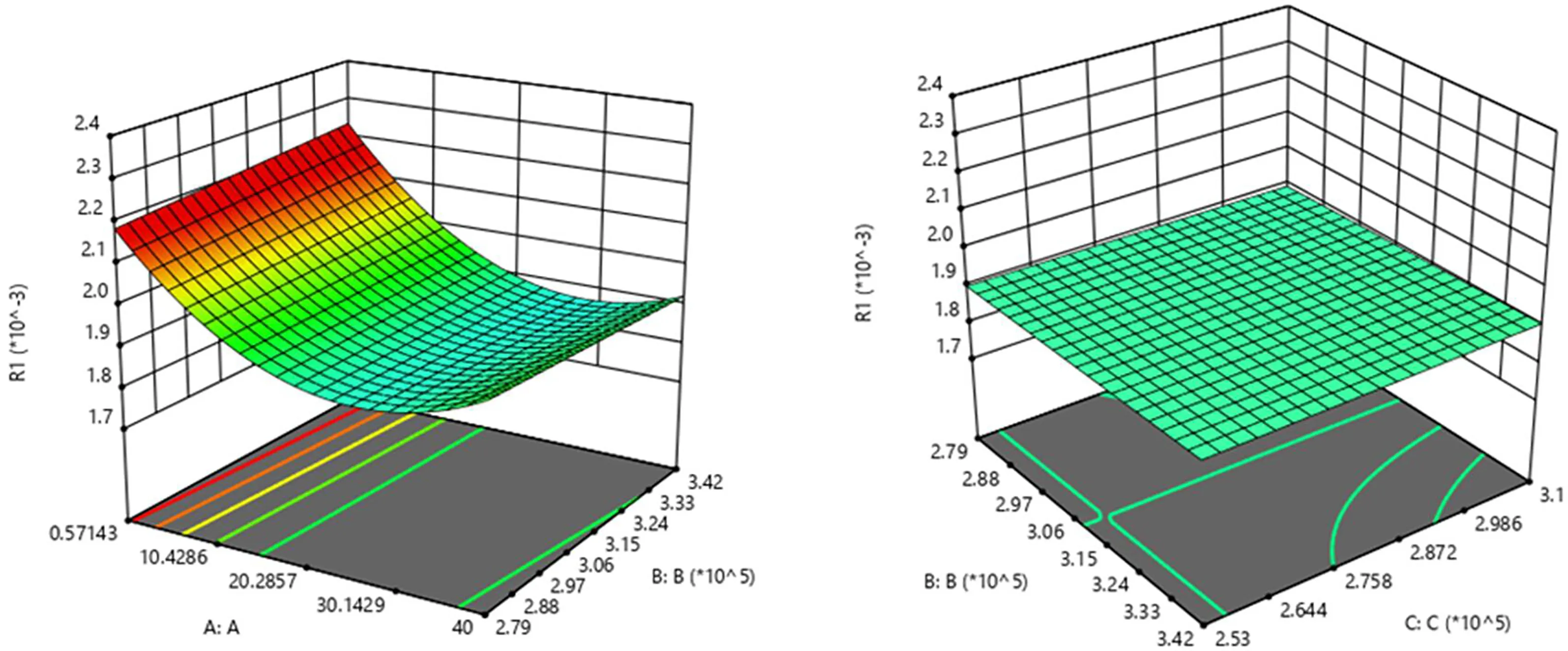
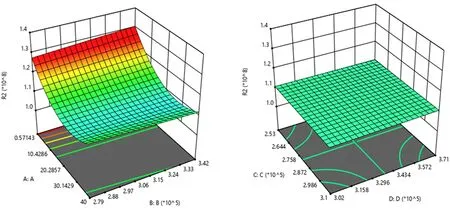
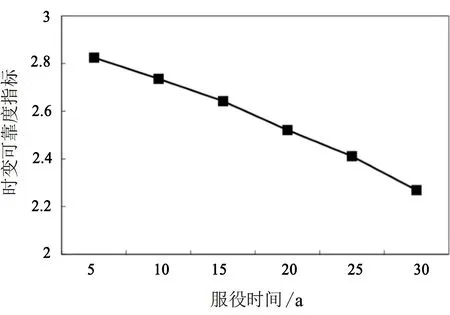
Pf(t)=P(R(t) (5) 式中,T为动臂结构的设计使用周期。 在实际应用中,采伐机动臂的抗力会随着服役时间的增加而表现的越来越小,所以动臂结构的时变抗力模型通常可以描述为结构初始抗力和抗力衰减函数的乘积。即: R(t)=R0(t)·φ(t) (6) 式中,R0(t)为动臂结构的初始抗力,初始抗力的均值与时间的起点无关,可表示为R(0);φ(t)为动臂结构的抗力衰减函数,一般为一确定性函数,表示为φ(t)=exp(-kt2);k为抗力退化速率。 森林采伐机动臂为左右对称封闭式中空箱形焊接结构,主要承受其自身重力,以及工作装置、液压缸的力或力矩作用,受力复杂,不能采用传统材料力学方法对其进行受力分析,为得到真实有效的载荷时变模型,故对其采用有限元分析方法建立模型,如图1所示。 图1 动臂结构 本文采用某15t履带式森林采伐机动臂为研究对象,其中动臂结构使用Q345(16Mn)材料,弹性模量为2.05×1011Pa,泊松比为0.3,密度为7.8×103kg·m-3。对其建立有限元三维实体模型。 对于采伐机动臂来说,其主要的工作形式就是动臂围绕支座的转动,所以需要约束采伐机动臂与支座铰接处销轴的UX、UY、UZ、ROTX、ROTY,而释放ROTZ,同时在采伐机动臂与其它构件铰接处施加载荷边界条件[13,14]。由于构建的是采伐机动臂时变可靠性模型,故采用瞬态有限元分析方法。 选取动臂最危险工况位置构建其载荷边界条件,可得载荷的随机变量分布,如表1所示。 表1 动臂随机变量分布 根据确定的采伐机动臂载荷及约束情况,对上述工况进行瞬态有限元计算,得到该试验下采伐机动臂的等效应力分布图和变形图,如图2所示。对结果分析可得该试验下应力集中部位、危险截面发生部位、变形量最大部位以及对应的时间关系。 图2 动臂有限元分析结果 2.2.1 RSM(响应面)方法 RSM方法起源于实验设计,其主要思想是针对于隐式或者需要大量计算得到的功能函数或极限状态面,用一个二次多项式来近似代替,进而求得可靠度指标的方法。本文应用有限元数值计算结果来拟合响应曲面[15]。 (7) 式中,a、bi、ci和dij为待定系数。 根据上述实验内容,将采伐机动臂结构的随机变量作为输入指标,各时刻对应的最大等效应力和形变量作为输出指标拟合响应曲面,可得采伐机动臂载荷效应的功能函数,如图3、图4所示。 图3 动臂应变响应面 图4 动臂应力响应面 Sdeformation(t)=2.33945-0.0140764t-0.155781Fb-0.00350699Fc+0.0422054FcFd(t)+0.000447313t2 (8) Sstress(t)=1.37047-0.00841479t-0.0944815Fb-0.0020963Fc+0.0235127FcFd(t)+0.000267371t2 (9) 2.2.2 采伐机动臂功能函数 由式(6)和式(8)可得采伐机动臂强度功能函数: G(t)=R(0)exp(-kt2)-1.37047+0.00841479t+0.0944815Fb+0.0020963Fc-0.0235127FcFd(t)-0.00026737t2 (10) 由式(6)和式(9)可得采伐机动臂刚度功能函数: G(t)=R(0)exp(-kt2)-2.33945+0.0140764t+0.155781Fb+0.00350699Fc-0.0422054FcFd(t)-0.000447313t2 (11) 在役采伐机动臂结构的时变可靠性分析是一定时间、条件和功能下的失效概率预测。设该15t履带式森林采伐机的服役期为30a,取时间步长为5a,抗力退化速率K为0.0005,利用iTRPD方法对其进行可靠度指标计算,计算结果如表2、表3所示。 图5 臂架强度时变可靠度指标 表2 采伐机臂架强度分析 表3 采伐机臂架刚度分析 图6 臂架刚度时变可靠度指标 建立森林采伐机动臂结构的时变可靠性数学模型,通过实际工程算例得出抗力均值、时变可靠度指标随着时间的累积,在逐渐降低;森林采伐机动臂结构结构的抗力均值、时变可靠度指标在服役年限前期退化较缓慢,在服役年限后期退化的较迅速,说明此森林采伐机动臂结构在服役过程中,各项功能特性在显著退化,需要加强对其进行定期的安全检测与评估;对于工程结构来说,考虑时间累积效应所得到的时变可靠度指标更加科学合理,也更加符合工程实际。2.1 动臂结构抗力的时变模型
2.2 动臂结构载荷的时变模型


3 可靠度指标的计算

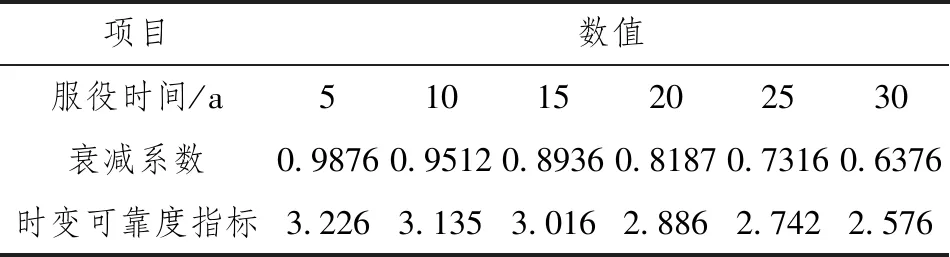
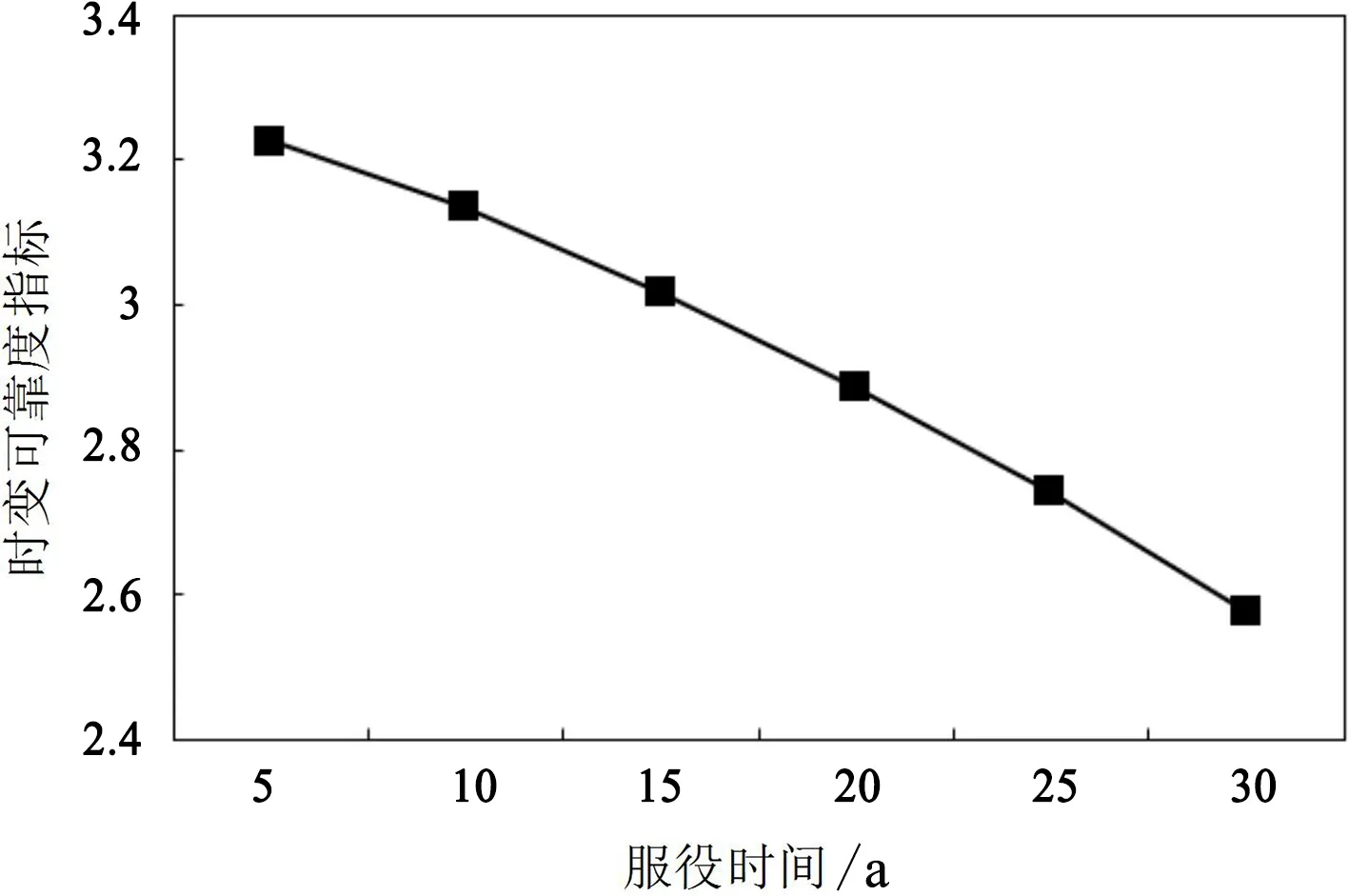
4 结论
