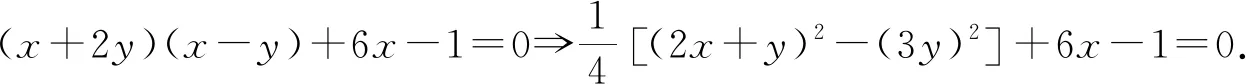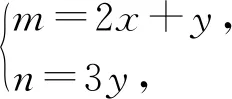基本不等式的别证及其它

江西省抚州市教育发展研究中心 (344000) 常家慧

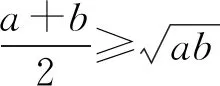
最值原理设x>0,y>0．

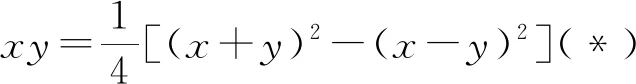
例1设x,y∈R，满足4x2-5xy+4y2=5，求x2+y2的取值范围．

例2 设x,y∈R，满足x2+4xy+y2=2，求x+2y的取值范围．

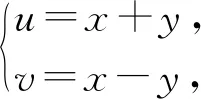
例3 设x,y∈R，满足4x2+6xy+9y2-2x+6y+2=0，求4x-y的取值范围．

例4 设x,y∈R，满足x2+xy-2y2+6x-1=0，求S=16x2-8xy+y2+1的取值范围．