基于一核、四层、四翼评价体系的试题分析——以2021年新高考Ⅰ卷第19题为例

江苏省苏州市吴县中学 (215151) 康小峰

1.背景分析

2020年初，教育部考试中心发布了《中国高考评价体系》，高考评价体系主要由“一核”、“四层”、“四翼”三部分组成, “一核”为核心功能,即“立德树人、服务选才、引导教学”,回答“为什么考”的问题; “四层”为考查内容,即“核心价值、学科素养、关键能力、必备知识”, 回答“考什么”的问题; “四翼”为考查要求,即“基础性、综合性、应用性、创新性”, 回答“怎么考”的问题.高考评价体系是高考命题、评价与改革的理论基础和实践指南,2021年新高考Ⅰ卷是在该评价体系下成功命题的一个典范,本文以此卷第19题为例从“一核”、“四层”、“四翼”三个维度加以分析,旨在更好的指导今后的高中数学教学,不当之处敬请同行批评指正.

2.试题呈现

(2021年新高考Ⅰ卷第19题)记△ABC的内角A，B，C的对边分别为a，b，c．已知b2=ac，点D在边AC上，BDsin∠ABC=asinC．

(1)证明：BD=b；

(2)若AD=2DC，求cos∠ABC．

分析：本题以三角形为载体，围绕常见的边角关系来设计问题，考查学生利用正弦定理和余弦定理来解决三角综合问题的能力，题设中——点D在边AC上，使得原本单个三角形变成了复杂图形，给人一种似曾相识的感觉.本题第一问直接用正弦定理便可得证,第二问内涵丰富,因此会有不同的思路,下面先给出4种解法.

解:(1)略.

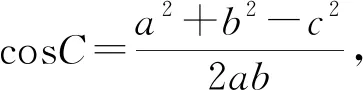
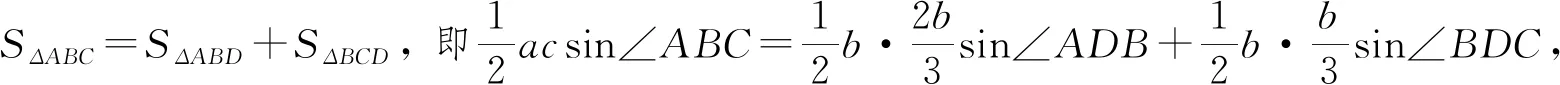
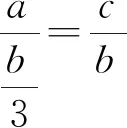
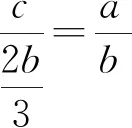
3.试题分析

3.1 体现高考的核心功能

本题第(1)问起点低，面向全体学生，让所有学生都有所得；第(2)问综合性较高，体现了“多层次、高落差”的特点，“多层次”体现为试题在难度设计上呈现出难度和思维的层次性，给学生提供了多种解决问题的途径，让不同层次的学生都有发挥的空间.“ 高落差”体现为在试题的难度设计上不仅有层次性，而且在思维的灵活性、深刻性，方法的综合性和创造性等方面,为优秀的学生提供施展才华的空间.如果第(2)问采取前三种解法则耗时较多，影响后续试题的解答，反之，若采取创新性的解法四，则解答省时省力，有利于考生腾出更多的时间去主攻导数压轴题，四种解法能有效甄别出不同思维的考生，从而展现出高考的选拔性功能.

该题很好的体现了“教材起点，高考落点“的高考命题原则，很多解题方法都是源自课本，比如解法二利用邻角互补的余弦值互为相反数，便来自于苏教版数学必修5教材第16页例6的求解方法.

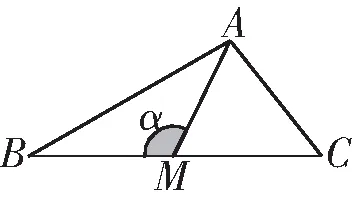
图2

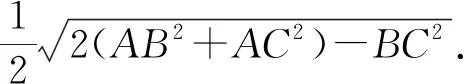
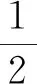
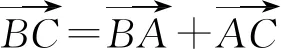
上述案例向我们一线教师传递出这样一个信号, 教材是一切知识的载体，一切命题的源泉，虽然新高考在情境载体、考查内容、试题结构等方面进行了有效的尝试和突破，但面对新高考我们绝不能以题海战术来代替课本教学，而是要扎扎实实的立足课堂用好课本，注重引导学生经历数学知识发生、发展的全过程，充分挖掘典型问题的内在价值与迁移功能，让学生感到学有所用，在潜移默化中提高 “四基”发展 “四能”，促进学生核心素养的形成.

3.2 体现“四层”的考查要求

根据高校人才选拔要求和国家课程标准，考试评价的规律，高考评价体系将考查的素质教育目标凝练为“核心价值、学科素养、关键能力、必备知识”的“四层”考查内容.

核心价值是指即将进入高等学校的学习者应当具备的良好政治素质、道德品质和科学思想方法的综合，是在各学科中起着价值引领作用的思想观念体系，是其在面对现实的问题情境时应当表现出的正确的情感态度和价值观的综合.数学是培养理性思维的学科，有助于学生树立科学精神和科学态度，有助于学生形成正确的人生观、世界观和价值观,比如本题以研究三角形中边与角的关联关系为切入点，要求学生在解决问题时，树立战胜困难的信心和勇气，要有百折不挠、契而不舍、刻苦钻研的探索精神，会用联系、运动和发展的辩证思维深入地思考和探究，从而突出试题的理性思维，彰显出数学的理性精神.

必备知识是指是指即将进入高等学校的学习者在面对与学科相关的生活实践经验或学习探索问题情境时，高质量的认识问题、分析问题、解决问题所必须具备的知识.本题是学习探索创新情境题，考查的是高中数学必备知识——解三角形及其向量.在试题设计中体现了“主题单元教学”理念，以解三角形核心考点为主线，把解三角形的相关知识(正弦定理、余弦定理、面积公式等)串联在一起，考查完整知识体系建构情况以及在知识交汇处灵活运用转化进行求解的策略.体现出高考在设计考查内容时，更加注重知识的系统性、整体性、结构性和交汇性.

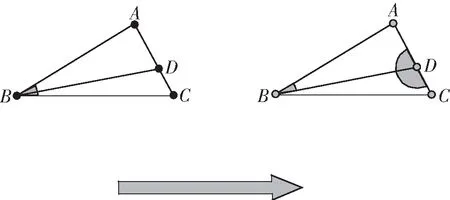
SΔABC=SΔABD+SΔBCD图3

关键能力是指即将进入高等学校的学习者在面对与学科相关的生活实践经验或学习探索问题情境时，高质量的认识问题、分析问题、解决问题所必须具备的能力.高考评价体系对高考数学科提出5大关键能力：逻辑思维能力、运算求解能力、空间想象能力、数学建模能力和创新能力.本题的不同解法，反映出不同的能力.解法一是解三角形中常见的解题思路，解法二和解法三考查了学生的逻辑思维能力、运算求解能力和数学建模能力.解法四是在认真分析现有图形与原有认知结构中的异同之后，通过变换面积视角并借助于三角形相似得出的，整个方法新颖、简洁、给人眼前一亮的感觉，展现了学生高水平的直观想象、数学建模、创新实践等关键能力，同时对数学语言表达能力的逻辑性和条理性也提出了更高的要求.

3.3 体现“四翼”的考查要求

“四翼”立足于素质教育应达成的内容表现与形式表现，是联结“四层”高考考查内容与高考命题实践的纽带，不仅是评价学生素质高低的基本维度，也是评价高考试题质量优劣的基本指标.

在“基础性”维度上，试题将三角形、三边长关系、边角关系等多个数学对象组合在一个情境中，由于没有给出图形，需要考生根据题意画出图形，在厘清图形中边、角关系后，考虑从两个方向切入：①将已知量全部集中在一个三角形中，利用正、余弦定理求解；②已知量与未知量涉及两个或两个以上的三角形，先考虑解条件充分的三角形，再逐步解其它三角形,然后展开分析与求解的过程.第(1)问考查了正弦定理的直接应用，第(2)问考查了余弦定理，利用第(1)问的结论和题设条件，结合课本中解三角形问题常见的处理方法便可以求解，整个求解过程无不在考查学生的基础知识、基本技能、基本思想方法和基本活动经验，可见试题注重情境的典型性、数学知识的基本性和求解策略的通用性，很好的体现了“四翼”的基础性.

在“综合性”维度上，本题第一个综合点是如何求线段BD长，题目给出的两个条件,一个是边的关系，另一个是边角混合关系，结合目标消角是关键，综合考查了学生分析问题的能力和消元的数学思想；第二个综合点是寻求三边a,b,c的关系，难点表现在两个方面：一是如何用好BD=b及线段BD在ΔABC中的位置；二是如何找到切入点列出关于a,b,c的等式，需要根据自身积累的数学解题经验并调动认知结构中现有的解题模型方可解决问题，学生要具备较强的直观想象能力和数学探究能力.

在“应用性”维度上，本题打破传统意义上用正、余弦定理来解三角形的解题套路，运用向量方法，亦可用平几知识中的三角形相似来求解，展现出“应用性”的丰富内涵.

在“创新性”维度上，试题的呈现没有出现在第17、18题位置，而是破除原来固有的模式，直接出现在具有区分度位置的第19题，体现出三角函数解答题题序的创新.高考结束后与一些学生交流得知，考试时感觉第(2)问看起来常规，但又不知如何下手，硬是浪费了不少时间，可见该题的理性探索之深刻，命题思路之深邃，体现了试题的灵活性与创新性，展现了稳定与创新的融合.而创新性的解法四，更可以考查学生的综合素质和创新精神，体现出命题者的良苦用心.其实，该题的创新性远不止于上述分析，还体现在试题的可推广性，比如将原题中的AD=2DC改为AD=λDC(λ>0)，试题的考查深度将更加深入，也可以更好的突出数学本质.

4.结束语

通过“一核”、“四层”、“四翼”对2021年新高考Ⅰ卷第19题的分析，试题很好的贯彻了高考评价体系的核心理念，以“立德树人”为宗旨，突出数学本质，倡导学以致用，聚焦核心素养，发挥数学科的选拔功能，从根本上体现了素质教育的要求，为今后的高中数学教学起到了积极的导向作用.