丙型肝炎病毒感染流行病学模型的全局动态

崔景安，冯振洲，郭松柏

(北京建筑大学 理学院，北京 102616)

常见的丙型肝炎简称“丙肝”，是由丙型肝炎病毒(Hepatitis C Virus,HCV)引起的一种肝脏疾病[1]，主要经输血、针刺、吸毒、性接触等方式传播.它是导致慢性肝病、肝硬化和肝细胞癌的主要原因，也是许多国家肝移植最常见的适应证.根据世界卫生组织统计，全球丙型肝炎病毒(HCV)的流行率约3%，即感染人数约有1亿7千万[2]，另外相关数据表明，大约10%～20%的急性丙肝患者会自发地清除病毒并产生自然免疫力，在急性期结束后，约55%～85%的HCV感染者会发展成慢性HCV感染，在慢性HCV感染者中，肝硬化的风险在20年内介于5%至15%，2%至4%的感染者也可能发展为肝癌[3].除此之外，由于它的易感人群分布广泛，加上它的预后很差，因此已对全球公共卫生构成了重大威胁.

目前，数学模型是评价各种传染病传播性、预测未来发病率和评价防治效果的有效方法[4-11]，已被广泛应用于HCV感染的动力学研究.例如，DEUFFIC等[12]研究了按年龄和性别划分的丙型肝炎数学模型，他们指出了20世纪40年代从法国开始流行丙型肝炎，并预测了这种疾病的传播；MARTCHEVA等[13]引入了一种具有慢性感染阶段的丙型肝炎的流行病学模型，他们的模型不包括恢复(或免疫)类，属于SIS模型，他们的研究表明，在一定的标准下，无感染状态是全局渐近稳定的，而地方性非均匀稳态是局部渐近稳定的，为了控制这种疾病，应降低感染和慢性个体的有效传播率；YUAN等[14]提出了一种具有指数变化的种群急慢性阶段的SEIV模型，其中慢性感染者可恢复易感性，得出两个平衡点：无病平衡点和地方病平衡点，这两个平衡点的稳定性由基本再生数控制，他们更多关注慢性期对呈指数增长或衰退的人群的疾病传播和行为的影响；CUI等[4]也提出了一种急性和慢性丙型肝炎的流行病学模型，并对该模型的局部和全局动力学进行了研究.他们强调急性丙肝患者可以自行消灭病毒，进入恢复类，而慢性丙肝患者不能自动消灭病毒进入恢复类，因此有相当一部分患者最终发展为肝硬化或肝细胞癌.

众所周知，疾病发生率在传染病模型中起着至关重要的作用.常见的疾病发生率包括双线性发生率、饱和发生率、标准发生率和非线性发生率.对于SI或SIS传染病模型，标准发生率已被广泛地研究过[15-17].然而，对于SICR传染病模型，较多的研究者关注的是双线性发生率或非线性发生率，标准发生率还较少被研究.受以上工作启发，在CUI等[4]对丙肝模型的研究基础上，考虑了具有标准发生率函数的微分方程的动力学模型，这样的改变也是基于人和群居动物来说，标准发生率更加符合实际.

本文的其余部分组织如下：在第一节中，建立了模型并求得了基本再生数；在第二节中，通过构造适当的Lyapunov函数证明了R0≤1时无病平衡点的全局稳定性；在第三节中，在特定条件下通过极限系统获得了R0>1时地方病平衡点的全局稳定性.

1 模型的建立

建立的传播动力学模型如下：

(1)

这里S(t)，I(t)，C(t)，R(t)分别表示易感者、急性感染者、慢性感染者和恢复(或免疫)者个体的数量，其中，模型参数的生物学意义列于表1，所有参数均为正数，人口总数用N(t)=S(t)+I(t)+C(t)+R(t)表示，并满足以下方程式：

(2)

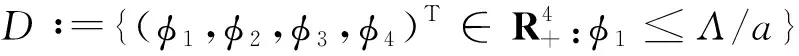
表1 模型参数的生物学意义

2 无病平衡点的稳定性

定理1如果R0<1，则模型(1)的无病平衡点P0是局部渐近稳定的.

证明通过计算模型(1)在P0处的Jacobian矩阵，得到特征方程为如下形式：

(λ+a)2(λ2+A1λ+A2)=0.

(3)

其中A1=2a+μ+γ-β>(a+γ)(1-R0),A2=(a+γ)(a+μ)(1-R0).

易知，方程(3)中有重根λ=-a<0.因为R0<1，所以有A1>0，A2>0.从而由Routh-Hurwitz判别法可得，无病平衡点P0是局部渐近稳定的.

定理2如果R0<1，则模型(1)的无病平衡点P0在D上是全局渐近稳定的.

证明由定理1知P0是局部渐近稳定的.因此，只需要证明P0是全局吸引的.设u(t)=(S(t),I(t),C(t),R(t))T是模型(1)过任意φ∈D的解.记ω(φ)为关于模型(1)的φ的ω极限集，即只需证ω(φ)={P0}.在D上构造如下V函数：

V(φ)=(a+μ)φ2+βφ3.

易知V在D上连续.于是V沿模型(1)的解u(t)的导数为

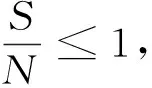
对于任意φ∈ω(φ)⊆D及R0<1，有ω(φ)≥(a+γ)(a+μ)-β(a+μ+pγ)=(a+γ)(a+μ)(1-R0)≡ω0>0.且由ω0b(φ)=0，可得I=0，根据文献[19]中的定理3.2，对于任意φ∈ω(φ)，都有I=0.

令ν(t)=(S(t),I(t),C(t),R(t))是模型(1)的解，由ω(φ)的不变性可证，对于t∈R有ν(t)∈ω(φ).因此对于t∈R都有I=0，利用模型(1)和ω(φ)的不变性可得ω(φ)={P0}.

3 地方病平衡点的稳定性

定理3如果R0>1，则模型(1)的地方病平衡点P*是局部渐近稳定的.

证明通过计算模型(1)在P*处的Jacobian矩阵，得到特征方程为如下形式：

(λ+a)(λ3+α1λ2+a2λ+a3)=0.

(4)

这里

进一步计算有

因此对于R0>1，可得a1>0,a3>0且a1a2>a3，从而由Routh-Hurwitz判别法可得，地方病平衡点P*是局部渐近稳定的.

定理4如果R0>1且μ=0，则P*在集合D0={φ∈D|φ2>0}中是全局渐近稳定的.

证明易证D0是模型(1)的一个正向不变集.由定理3知，P*是局部渐近稳定的，故只需证P*是全局吸引的，即证ω(φ)={P*}.首先利用文献[20-21]中的系统持久性方法可获得模型(1)是一致持久的.

可得到模型(1)的如下极限系统：

(5)

显然对于R0>1且μ=0,P*也是系统(5)的一个唯一的正平衡点.故由文献[4]中的定理3.2和定理4.2可得P*是全局渐近稳定的.于是Ws(P*)=D0，其中Ws(P*)是关于系统(5)的P*的稳定集.显然ω(φ)∩Ws(P*)≠Ø.因此，由文献[22]中的定理1.2可得，ω(φ)={P*}.

4 结 论

依据丙肝的传播机理，构建了一类具有标准发生率且总人口在变化的丙型肝炎流行病的动力学模型.首先根据下一代矩阵方法给出了模型的基本再生数R0，然后利用Routh-Hurwitz判别法给出了无病平衡点以及地方病平衡点的局部稳定性，并通过构造适当的Lyapunov函数和ω(φ)不变性证明了当R0<1时，无病平衡点是全局渐近稳定的；当R0>1时，地方病一致持久，且在特定条件下地方病平衡点是全局渐近稳定的，对丙肝的局部和全局动力学做进一步的研究.