高校学生成绩的聚类数据集划分为导向的教学思路探讨
2022-03-04顾偲雯沈新逸王加安句爱松
顾偲雯 沈新逸 王加安 句爱松
(1.常州工学院光电工程学院,江苏 常州 213032;2.大连理工大学化工学院,辽宁 大连 116024)
0 引言
学生的学习成绩是其对课程学习的掌握程度的一个重要体现,也是反映教师教学效果好坏的一个重要标准。 现今,随着高校的扩招,高校内的师生数量与日俱增。 学校内部的数据库已经积累了海量的数据,然而缺乏信息知识与技术,管理者往往无法在这大量的数据中提取到有用的信息[1]。 只能运用传统的排序及统计功能取得一些表层的信息。 怎样使用学生某一阶段的成绩提炼分析出有用的信息来提高之后的教学方案与学生成绩有着至关重要的意义。
学生成绩的评价的一般方式是将其粗略的划分为优秀、良好、中等、及格与不及格等几个等级[2]。 这种评价方式虽然简单方便, 但却存在着一些不合理性,比如有些课程的难度较高, 学生的普遍成绩都不高,这时使用这种方法就很难在学生之中划分出不同的群体。 如果可以把聚类分析实际应用于成绩分析之中,就可以通过动态的分析得到比较准确合理的划分结果[3,4]。
本文将k-means 聚类和层次聚类方法用作成绩及其影响因素的分析,利用MATLAB 软件实现聚类算法的实际应用,建立数据分析模型并对聚类结果进行评价,最后总结学生成绩提高的途径。
1 确定数据结构
本文选取了本高校学生的高等数学上/下,大学英语上/下, 大学物理上/下, 计算机基础与三门专业课(电工基础、工程制图、单片机原理)等共十门课程的学生成绩作为样本数据来进行分析。 每个班的学生成绩均为百分制形式。
把来自不同数据源的数据集中到一起,以便后续的分析和处理。 主要是规范处理不同数据源中数据的词义、名称、结构等不同,以形成适合做聚类分析的样本数据。 本文将三个班的学习成绩集中整理成一张成绩表。
另外,本文对采集的数据进行清洗,主要是要清除或补全样本数据中的残缺数据、错误数据、重复数据。 若有某学生的大部分成绩为空白值,则不录入该学生的所有数据信息,如果成绩信息中出现单个空白值,则计算出平均成绩进行填充。 部分原始数据经过处理后如表1 所示。

表1 预处理后的部分数据表—成绩
此外,绩点也是衡量一个学生学习质量的一个重要指标, 本文收集绩点、 学生旷课数量 (包括晚自习)、补考课程数目等数据,经过筛选和整理后得出的结果用作聚类分析。 数据经过预处理后部分数据如表2 所示。

表2 预处理后的部分数据
2 成绩数据集划分
2.1 问题描述
高校举行的各科目考试使学生的学习成效得以以数字的形式表现, 其不仅能反映出教师的教学水平,还可以使学生得知自己的优势与不足之处,进而协助教师与学生及时发现问题并能得以改进。 然而目前的普遍方法是对学生成绩做简单的数据统计处理,这种方法虽然简单,但不足之处是费时且费力,而且还不一定能得到有用的反馈信息。基于此,将k-means算法运用到学生的各科成绩中分析各类学生的薄弱方面并提出改进方案,以及对可能影响学生成绩的相关因素进行分析。
2.2 选取最佳聚类数
在k-means 聚类最优的k 值选取中常用的方法为“手肘法”。 手肘法的核心指标是SSE (Sum of the Squared Errors,误差平方和)[5]:

其中,Ci是第i个簇,p是Ci中的样本点,mi是的质心(Ci中所有样本的均值),SSE是样本数据聚类后的总误差平方和,其值越小,聚类结果越好[7]。 当k等于5 时, 误差平方和的下降趋势开始逐渐变得缓慢,所以这点对应的就是肘部位置。
2.3 学业成绩聚类分析
在MATLAB 软件中对预处理后的数据集直接调用k-means 函数[8]并选择聚类数为5 后得出聚类结果如表3 所示。

表3 成绩聚类结果表
表内数据为每一类学生的平均成绩,即分类后各类的聚类中心。 相应地,给出各类学生占比分布如图1 所示,图中用数字1、2、3、4 和5 来分别表示学生的类别。

图1 学生分类数量占比图
从表3 和图1 的聚类结果中可知,分析各类学生课程成绩中的优势与弱势学科可以帮助课程教师改进教学方案。 每类学生成绩特征与解决方案如下:
第一类学生占比为33%,人数最多,除了英语成绩稍低,其他课程成绩都还不错,可能是对英语的学习存在忽视或者偏科,这类学生需加强英语方面的学习,其他课程继续保持即可。
第二类学生占比为15%,人数占比较小,但所有科目成绩几乎均在及格线左右, 此时就需要这类学生自我反思,是不是学习方法出现了问题,或者是上课并没有认真听讲,没有独立完成作业,教师则要加强对这类学生的监督管理, 否则可能无法达到毕业要求。
第三类学生占比为24%,这类学生的所有课程成绩都比较优秀,除了单片机原理及接口技术,其他成绩均在80 分往上, 此类学生只需稍微加强单片机方面课程的学习, 在其他方面可适当减少一些学习时间,用于参加社会实践,为踏入工作做准备,或者用于毕业升学所需要学习的课程上。
第四类学生占比为20%,此类学生大部分课程成绩属于中等偏下水平,尤其是高数和英语成绩均处在及格边缘, 可能是在前期的学习中基础打得不够扎实,需要增加在高数与英语方面的学习时间,尤其是高数,因为在后面需要学习的专业课程中大部分都需要有扎实的数学基础。
第五类学生占比为8%, 此类学生的总体成绩与第四类学生的成绩相差不大, 大多处于中等偏下水平,唯一的区别在于单片机原理及接口技术这门课程上,这门课程的成绩低于及格线十几分,是所有学生中这门课程成绩最差的一类,对于这一类学生,老师可以多加关注,给予鼓励,并建议这类学生向专业课程学习的不错的同学多多请教,改进自己在专业课上的学习方法,吸取经验。
2.4 层次聚类与k-menas 聚类对成绩影响因素的分析
本文将分别使用层次聚类方法与k-means 聚类方法对数据集进行聚类分析, 为使聚类结果有可比性,两种聚类方法都将聚类数目设置为三类。 结合图像可更直观的展示数据之间的联系,也更方便用于对比,所以本文将运用MATLAB 软件的plot 函数[9]将聚类结果使用三维图像的方式展现出来, 并用imagesc函数[10]将聚类结果的相关程度表现在二维平面上以供对比。 得到k-means 方法聚类结果如图2 所示,kmeans 聚类结果相关程度如图3 所示。

图2 k-means 方法聚类结果图
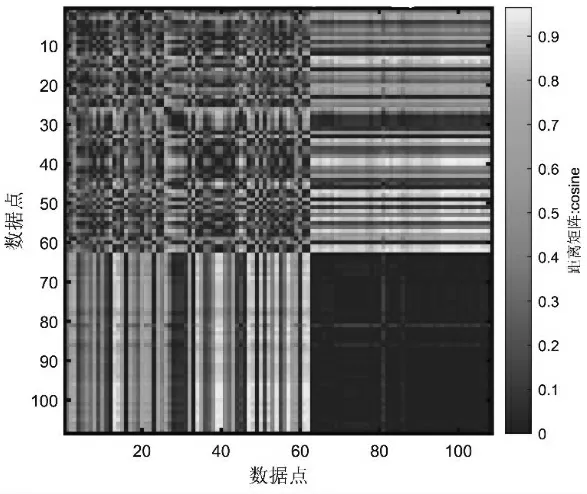
图3 k-means 聚类结果相关程度图
同理得到层次聚类方法聚类结果如图4 所示,层次聚类结果相关程度图如图5 所示,层次聚类法层次结构图如图6 所示。

图4 层次聚类方法聚类结果

图5 层次聚类结果相关程度图

图6 层次聚类法层次结构图
分析上述结果可知,两种聚类方法运行后的结果存在区别,但划分后各类内的数据点大致相同。 由于在文内给出的三维视图不能像在软件中一样自由转动,所以将绩点、学生旷课数与课程补考数投在二维平面上可以更加直观地发现内在的联系。 将绩点从4.5 开始每间隔0.5 划分一个等级,共划分出A、B、C、D、E 五个等级,然后将所有数据导入MATLAB 软件中运用plot 函数可得数据点分布如图7 所示。

图7 数据点分布图
观察图7 可知, 数据点的聚集状态与聚类三维结果图相似, 绩点高的数据点都聚集在图片左下角,这意味着挂科数目与课程旷课数目越少,相对的学生的绩点越高。 说明这三者之间确实存在一定的线性关系。 因此,校方可以从学生的旷课情况入手,进行更为严格的管理措施,同时也应让学生意识到长期逃课的代价,做到警示的作用,让学生可以将更多的时间用于学习上,以此来提高学习成绩。
两种聚类方法虽然都成功产生了聚类结果,但是对相同数据的聚类结果之间却存在差异,说明两种不同算法的聚类方法可能会对聚类结果产生不同的影响。 观察图3 可知,横纵坐标是将数据矩阵按照大小顺序排列,再把各数据点的距离大小使用不同的颜色标记出来,颜色相近的数据点就说明其比较相关。 所以理论上来说按照大小排序后的数据矩阵各段之间应该更有可能被聚为一类,但是k-means 聚类结果相关程度图中的数据点之间的距离矩阵却排列杂乱,没有规则,左上角部分尤为明显,说明聚类结果可能并不是很准确,而图5 中则没有出现这种情况,各部分间的距离矩阵数据都有规则可循,所以聚类结果比较准确。
3 结语
学生成绩是评价教学质量的重要依据,也是评价学生对所学知识掌握程度的重要标志。 目前,多数高校的师生数量都达到了几万甚至十几万的规模。 学校内部的数据库已经积累了海量的数据,然而缺乏信息知识与技术,管理者往往无法在这大量的数据中提取到有用的信息,仅能运用传统的排序及统计功能取得一些表层的信息。 在此背景下,本文采用k-means 聚类方法进行分析, 并对比了层次聚类与k-means 聚类,得出了以下结论:相比于成绩评价的传统方法,聚类算法应用于成绩分析弥补了前者的不足,可以横向对比各类学生的成绩差异,而且可以更加准确定位到每一个学生, 将不同特征的学生成绩划分聚类后,能够针对各类学生成绩的特点重新规划教学方案,为任课教师提供了改进教学策略的有利依据。 同时,其也能显著减少资源的浪费和研究人员的精力投入,因为聚类算法能直接得出样本中各类间的差异信息,不再需要人员来逐个分析每个样本数据的特征信息,极大节约了社会资源。
