浅谈中学数学教材习题配置的若干问题

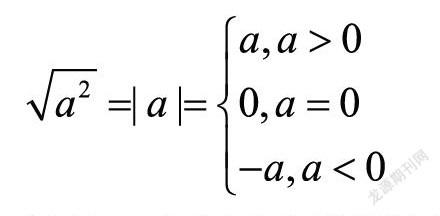
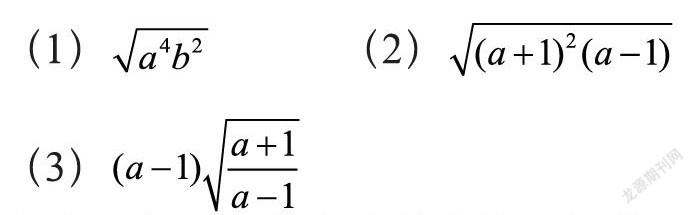
摘 要：学习数学知识离不开数学习题的练习，一本好的数学教材也必须配置高质量的数学习题。在教育制度发生重大变革的今天，数学教材习题配置问题仍旧是编写数学教材的重中之重。文章从习题的定义、习题的功能、习题的分类等多方面来阐述习题配置中的诸多问题，最后总结出习题配置的若干原则和方法。

关键词：初中数学;教材习题;配置原则;配置方法

中图分类号：G42                                  文献标识码：A                                       文章编号：2095-9192（2022）03-0091-03

引  言

加强解题训练是数学教学的重要任务。在日常教学中我们不难发现，一本优秀的数学教材，不仅要有准确的定理和概念叙述，还应有用于检测教学成果的习题。数学习题是数学教材中不可或缺的组成部分。毫不夸张地说，教师对课后习题的选择直接关系到课堂教学质量。

一、配置数学教材习题问题的提出

数学是目前基础教育学科中十分重要的学科之一，在新课程改革下的数学教学活动中，解题是衡量学生数学学习水平的最基本的检验方法。戴再平在《数学习题理论》中说道：“数学教育活动中，‘解题’是最基本的活动形式。无论是学生的数学概念的形成、数学命题的掌握、数学方法和技巧的获得，还是学生智力的培养和发展，都必须通过‘解题’来实现。同时，‘解题’也是评价学生的知识发展水平的主要手段。”[1]在传统教育观念中，解题就意味着解答习题，而在当今AI赋能高质量精选习题的情况下，每年数学教材中的习题设置都在发生变化。

习题是中学数学课本的重要组成部分。习题配备得好不好，直接影响到学生学习质量的高低。许多优秀中学教师的教学质量之所以高，一部分原因是习题选择和处理得恰当。教师在日常教学中不难发现，数学习题不仅仅是模拟性的习题，也有一些来自我们生产生活中的各种实际问题。学生在思考和解答这些问题时，也必然会促进自身数学思维能力的发展。

一本优秀的数学教材，不但要有准确的定理和概念，而且要配置高质量的课后习题。素质教育背景下，教师在日常教学中，不再一味地追求难题、偏题，而是立足教材本身，充分发挥教材习题的作用，进而提高课堂教学的效率与质量。数学习题的定义、功能、分类、选择、配置方法、配置原则是如何相互联系、相互影响的，决定着数学教材习题配置今后的发展方向。综上所述，笔者结合日常教学中的反思，对中学数学教材习题配置问题进行了探讨。

二、数学教材习题配置的特性

什么是数学习题？“习题”一词在《现代汉语词典（第7版）》中的解释是：“教学上供练习用的题目。”词典上的解释已经很好地说明了习题的作用，也让我们从侧面认识到习题对日常教学的重要性。数学习题是考查学生逻辑推理、数学计算、数学说理能力的题目，数学习题包含在习题范围内，因此习题所具有的特性它同样具有。

（一）数学习题的分类

按照题目所考查的内容，数学习题可以分为封闭题、综合题与发散题三种类型。封闭题是具有确定且唯一答案的习题，主要由选择题、填空题等组成，这类习题的特点是答案固定不变，用来考查学生对某些固定的数学知识点的掌握情况。综合题是考查知识比较全面的习题，如果一道习题涉及的知识点超出了某个单元或学科，那么这道习题就具有了综合题的特点。发散题是答案不唯一或条件不充分的习题，一般没有固定答案，可以让学生自己拓展，去寻求不唯一的答案，这类题目最大的特点在于能帮助学生提高举一反三的能力。

按功能数学习题分为课本例题、课后习题、模拟题、考试真題等。课本例题是对新知识定理、概念的实践和示范，强调培养学生学以致用的能力。课后习题是对课堂所学知识的熟悉和巩固。模拟题和考试真题用于检验学生数学学习水平，一般此类题目具有技巧性和典型性的特点，能筛选出不同水平的学生，同时让数学教师发现学生存在的问题。

（二）数学习题的功能

1.学习定理

通过数学习题，学生能系统地掌握数学定理，并熟练地运用数学定理解题，从而形成数学思维，提炼解题方法。

2.发散智力

通过数学习题的训练，学生的智力水平会得到提高，对数学基本知识和基本技能的运用能力会得到培养，同时学生的数学思维能力、解题能力也会得到提高。

3.评价成绩

学业成绩的检查与评定是整个教学过程的有机组成部分。在现行教育体制下，学生的成绩与规定时间内解题的数量和正确率息息相关，考评内容为基础知识掌握、识图水平、计算能力、说理表达等;而数学教学的考评主要侧重于计算能力和说理表达。

三、数学教材习题配置的原则

数学教材习题不应盲目进行配置，应遵循如下原则。

（一）目标性原则

在编写不同教学阶段的教材过程中，编者需要按照新课程标准和新的考试标准来精选习题，所配置的数学习题要具有明确的目标，避免盲目性，避免在同一层面上机械地重复。只有这样，才能达到预期的效果，起到锻炼和提高学生解题能力和学习能力的作用。例如，“二次根式”是初中数学对学生数域扩容的一项重要教学内容，而对二次根式的化简计算，学生应该都能记住下面的计算公式：

但是，在解决问题的过程中，学生对公式使用过程中符号的判定会出现些许问题。这就要求我们设置的习题更有目的性。比如，教师可以设置如下习题。

化简并讨论各题目中a、b的范围。

（1）            （2）

（3）

上述几个题目的难度是由浅入深的，这方面会在后面的循序渐进原则里再讲，每个题目都是针对公式中符号判断加以练习，从单个字母替换到整体思想的运用，目的在于提高学生在二次根式化简计算过程中符号判断的能力。

（二）指向性原则

教育教学需要因材施教，数学习题配置更要立足学生实际，具有指向性。习题配置应遵循精准分层，如果课后习题太简单，全部学生都可以轻松解决，就无法体现学生的个体差异，无法让部分学生获得成就感;课后习题太难同样也不可取，会使基础较差的学生产生畏难情绪，而基础较好的学生也容易忽视对基础知识和基本技能技巧的掌握，所以，我们强调难易适当。

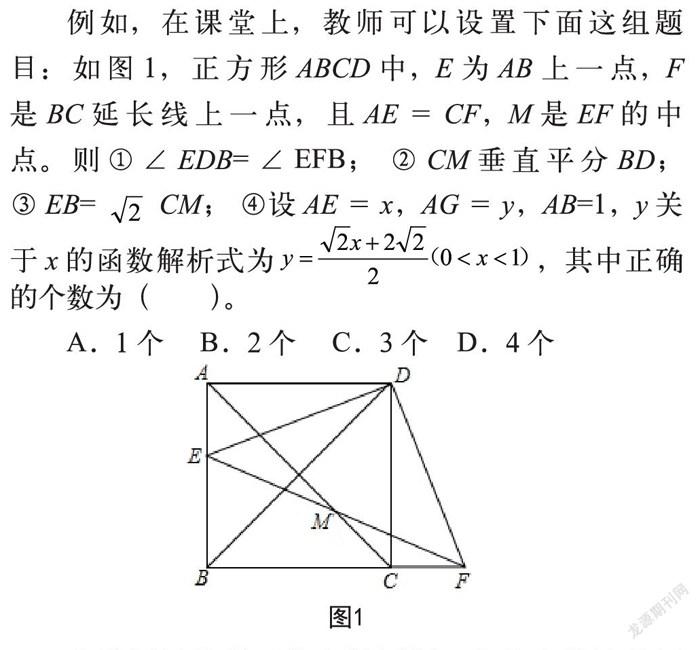
例如，在课堂上，教师可以设置下面这组题目：如图1，正方形ABCD中，E为AB上一点，F是BC延长线上一点，且AE=CF，M是EF的中点。则①∠EDB=∠EFB; ②CM垂直平分BD; ③EB=CM; ④设AE=x，AG=y，AB=1，y关于x的函数解析式为，其中正确的个数为（ ）。

A.1个     B.2个     C.3个    D.4个

这道题目体现了指向性原则，它是多结论的证明，每个结论的证明都需要用到题干里相同的条件，学生要自己判断调用哪个条件，但彼此之间又可以是递进的证明，前面的结论可以被用作后面结论证明的条件，学生可以根据自己的能力从结论①开始不断挑战，直到完成全部证明。

（三）循序渐进原则

数学不同于其他学科，中学阶段所学的数学知识就如“搭梯子”，前面的知识掌握不牢固，就好比底层的梯子没搭牢，无法越爬越高，势必会影响到后面知识的学习。因此，习题配置要始终把握循序渐进的原则，使知识点之间紧密联系，串联成线。例如，在教学“绝对值”时，教师可选用下列习题供学生练习。

①|2|-|-2|=___________

②若a=2.21，b=-4.79，則|a|+|b|=___________

③若|a|=7，则a=___________

④若a<0，则|a|=__________

⑤绝对值小于5的非正整数是___________

⑥已知|a|=5，|b|=4，求a+b的值

以上6个题按知识产生的过程，难度由浅入深。前3题可以在教学过程中让全部学生完成;第④⑤题可以只让部分学生在前3题的基础上完成;最后一题则是灵活度非常高的题目，可让学生进行分类讨论，让完成全部前5题的学生完成。这样循序渐进地提升习题难度，能让学生对绝对值的理解达到一定的高度。

（四）可操作性原则

回顾近几年的中高考数学试题，我们不难发现，与生活实际相关的数学真题呈逐年增长的趋势。这类题目不仅符合教学课程标准的要求，还充分体现了可操作性原则。这类数学题把我们的日常生活和新闻焦点结合在一起，有一定的综合性，有利于提高学生从生活中发现数学问题、解决数学问题的能力。因此，我们在数学教材习题配置中更应注重可操作性原则，将数学知识与日常生活联系起来，在解题中培养学生的数学学习能力，激发学生的学习兴趣、灵感、想象力。

例如，在教学“利用相似三角形测高”时，教师可设置实验性操作习题：在学校操场上选择合适的方法测量国旗杆的高度，并录制成小视频。

这样的习题设置能打破多年沿用的数学习题形式，使数学课从讲理论变成有趣的动手实操活动。这节课的内容本来就是学习3种利用三角形相似性测高的方法，学习之余配以这样的习题让学生走出教室，自己去获得解题需要的数据，自己寻找解题方法，自己建立数学模型图，能显著提高学生的学习能力。

（五）发展性原则

根据因材施教的教学原则，对于知识理解能力较强的学生，教师应主动为其创造发挥才能的机会和条件，使他们的数学学习能力得到充分发展，这与素质教育的要求是完全一致的。例如，在教学“等腰三角形”相关知识时，教师可以设置如下问题：

等腰三角形两腰上的高线相等吗？角平分线呢？中线呢？

几何图形应按照定义、性质定理、判定方法的顺序来学习，而几何题目也意在让学生用所学的定义、公理、定理来完成证明。上题在此基础上给学生提供了发展空间，证明高线相等不仅可以应用三角形全等知识，还可以用面积相等来证明，这样不仅用到了等腰三角形的性质，还发展了学生的思维能力。

四、数学教材习题配置的方法

中学数学教学内容不是孤立的客观存在，其内容既有独立性与特殊性，也有相互之间的关联性与普遍性。数学教学内容是一个复杂连贯且有规则的体系，而数学习题的配置必须是在难度上由浅入深，符合知识规律的。在日常教学中，教师必须先以书本习题为基础，由易到难，高质量地配置数学习题。一是由个性到共性，将数学知识同类型中个性与共性关系部分恰当结合，透过个性问题探索共性问题，通过对每道习题的分析，提炼同类型问题的解决方式，从而提升每道习题的思考价值;二是由一法到多法，充分结合教材所学内容，通过不同思维途径，利用正向逆向、具体抽象等多种解题方法，用数学语言启迪学生的发散性思维，让学生在获取知识的同时培养辩证思维能力;三是从一般到特殊，将数学解题中蕴含的发散思维发掘出来，可以设置一般方法难解、特殊方法易解的习题。

结  语

美国数学家克莱因曾说：“数学是一种理性的精神，使人类的思维得以运用到最完善的程度。”中学数学教学大纲也明确指出：“发展思维能力是培养能力的核心”“要重视学生在获取和运用知识过程中发展思维能力”。在中学教材习题配置已经日趋完善的今天，我们在实际教学过程中仍会发现，教材习题作为数学教学中不可或缺的一部分，其配置还不能完全满足不同学习水平的学生，还有值得商榷的地方。因此，持续研究教材习题配置问题，是每位一线教师不可忽视的责任。

[参考文献]

戴再平.数学习题理论[M].上海：上海教育出版社，1991.

作者简介：黄一川（1987.7-），男，河南洛阳人，任教于深圳福田外国语学校，中教一级，本科学历。