层状岩体损伤破坏特征数值模拟
2022-03-02代恒军
白 琦,代恒军
(中冶南方城市建设工程技术有限公司,武汉 430000)
1 研究背景
地质资料表明,沉积岩是最广泛分布于工程场地环境内的岩体。由于成岩年代的不同,沉积岩的最突出特征就是层状构造,因此研究层状岩体的力学特性对工程建设意义重大。
层状岩体的弹性本构关系可用横观各向同性模型来表达,层状岩体的许多本构模型研究均基于此。黄书岭等[1-2]建立了考虑多组结构面特性的层状岩体多节理本构模型,用来表述层状岩体的各向异性特性和应变硬化/软化特征。倪绍虎和肖明[3]研究了层状岩体的破坏特征,并进行了层状岩体的三维弹塑性有限元分析。梅松华[4]进行了层状岩体开挖变形机制及破坏机理的探讨,将层状岩体的破坏机理分为以下4种:张拉断裂、剪切断裂、塑性滑移和剪张断裂。
力学理论的发展大致经过3个阶段[5]:①材料力学与古典强度理论阶段,首先根据材料屈服极限、强度极限得出材料抗力,然后基于结构受力分析进行强度设计;②断裂力学阶段,首先测量材料断裂韧性与断裂阻力,然后根据含缺陷物体的力学响应和裂纹扩展准则,判断宏观裂纹是否会发生失稳扩展;③损伤力学阶段,主要研究宏观缺陷或裂纹出现前,材料和结构的性能不可逆劣化的过程,从而进行破坏预计。
自Kachanov[6]、Rabotnov[7]和Gurson[8]等提出和发展损伤力学以来,它已被广泛运用于工程力学和材料力学等领域。Lemaitre和Chaboche[9]基于连续损伤等效应变假设,在不可逆热力学框架下,推导了与广义热力学力共轭的损伤变量,建立了塑性损伤理论。Gurson[8]基于细观损伤力学,提出了有限大基体含微孔洞的体胞模型,运用体积平均化的方法从细观分析导出材料的宏观性质,描述微孔洞损伤对材料塑性变形行为的影响。Krajcinovic和Fonseka[10-11]考虑把扁平状的微裂纹用矢量描述,在不可逆热力学框架下采用热力学通量和共轭力矢量表达损伤变量演化方程,该矢量损伤理论可以引入多种相互独立的损伤。谢和平[12]提出了一个考虑裂隙岩体能量耗散和大变形的损伤因子,建立了裂隙岩体宏观损伤力学模型,并引入分形方法对裂隙岩体进行非连续变形、强度和断裂破坏的研究。
本文首先基于细观损伤力学理论,运用体积平均化的方法,推导了微裂纹对岩体弹性柔度矩阵的贡献;然后基于不可逆热力学框架,通过一定的假设,推导了微裂纹矢量损伤破坏的过程;最后建立了层状岩体的损伤破坏本构模型,并通过数值计算与室内试验结果的对照,验证了该模型的适用性。
2 微裂纹对微元体总应变的影响
细观损伤力学研究表明,有效弹性变量与微裂纹参数的函数有关。微裂纹参数(最简单的如微裂纹密度)经常在非相互作用近似(NIA)的框架内引入。目前来看这种框架或许是唯一现实的方法,因为由不均匀相互位置的统计数据所支配的相互作用效应显然不能仅由微裂纹密度解释。
在具有代表性体积V的微元中处理半径为a(m)的N条随机分布的微裂纹,微裂纹密度ρ的表达式为
(1)
如果微裂纹的取向非随机,则微裂纹密度可用二阶张量表示为[13]
(2)
式中nn是表示微裂纹方向的坐标张量。
任何给定的微裂纹取向,都可以用α的3个特征值[α1,α2,α3]来唯一表征,它们以一种整体的方式反映了控制有效弹性分配的所有细节。α是一个对称二阶张量,因此任何取向分布的微裂纹对整体弹性柔度矩阵的影响都表现为正交对称性,对称轴与α的3个主轴重叠。
对于应力场σ中有孤立空腔的某微元体,该空腔表面上某点的位移将对该微元体的总体积应变产生额外应变Δεij,其表达式为
(3)
式中:u是应力场σ引起的位移矢量;n是空腔表面的法向矢量;S是空腔表面积。
对于含有孤立微裂纹的某微元体[14],式(3)可以表示为
(4)
式中[u]表示微裂纹两侧的位移不连续矢量,[u]=u+-u-。
如果该孤立微裂纹为平面裂纹,则有
Δεij=([bi]nj+[bj]ni)S/(2V) 。
(5)
式中:[b]为平面裂纹两侧的平均不连续位移,[b]=
(6)
由于微裂纹的存在,微元体的总应变可以表示为弹性应变和额外应变之和,即
(7)

Δεij=ΔSijklσkl。
(8)
于是有
(9)
式中Sijkl指考虑了微裂纹影响的总柔度张量。
3 层状岩体的有效弹性柔度矩阵
NIA框架是将微裂纹置于各向同性的基岩微元体中,分别计算微裂纹对基岩微元体的影响,再叠加得到所有微裂纹对基岩微元体影响的一种非相互作用近似的研究方法。在NIA框架下易知任何取向的圆形或椭圆形平面微裂纹对基岩微元体的影响。
根据上文的讨论,单个平面裂纹对应力场σ的响应而生的附加应变由平均不连续位移b确定。引入一个对称的二阶裂纹柔度张量B,该张量与裂纹处的应力场均匀分解牵引力t(m)=n·σ线性相关,使得[15]
b=B·t(m)。
(10)
在坐标系(n,t)中,t是微裂纹的切线,Bnn、Btt分别表示微裂纹的法向和切向柔度。这给出了t(n)在2个方向上产生b的法向和切向分量。非对角线分量Btn=Bnt表征了法向和切向的耦合,如果矩阵是各向同性,则Btn=Bnt=0。
由于B是一个对称的二阶张量,因此微裂纹柔度张量存在3个相互正交的主方向,在这些方向中的一个方向上应用均匀牵引力t(n)不会在其他2个方向上产生b的分量。在各向同性矩阵的情况下,n是一个主方向,另外2个由位于微裂纹平面上的单位向量s和t给出。因此,我们可以得到
B=Bnnnn+Bssss+Btttt。
(11)
B=BNnn+BT(I-nn) 。
(12)
其中,BN=Bnn。
对于半径为a的球形微裂纹,有:
(13)
(14)
式中:E0为初始弹性模量;υ0为初始泊松比。
由式(5)、式(10)及t(n)=n·σ,可得任意形状微裂纹引起的附加应变表述为
(15)
式中Bjk为微裂纹的柔度张量。
于是有
(16)
对于多个扁平微裂纹,采用NIA方法,则有
(17)
假定B张量是各向同性的,即BjkkIjk,则有
(18)
式中k表示形状因子。
对于半径为a的球形微裂纹,由式(12)、式(14)可得
Bjk=BT[Ijk-(υ0/2)njnk] 。
(19)
联立式(13)、式(16)、式(19)可得
(20)
忽略β项,将α作为唯一的微裂纹密度参数。由于α是一个对称的二阶张量,它的3个特征值为[α1,α2,α3]。因此,在NIA框架下,微裂纹的任何取向分布都等价于3个互相垂直的平行微裂纹族,具有相应的标量密度ρ1=α1,ρ2=α2,ρ3=α3,这也表明微裂纹的非随机取向分布会诱导岩体显示正交各向异性。
对于各向异性的基岩微元体,微裂纹密度参数α不足以表征微裂纹对附加柔度矩阵ΔSijkl的贡献,因为这些贡献不仅取决于任意选择的参考系中的微裂纹走向,而且还取决于微裂纹法向相对于材料各向异性轴的取向(与材料的刚性方向垂直的微裂纹比与材料的柔性方向垂直的微裂纹对整体柔度降低的影响更大)。这个困难在三维条件下更加难以解决,因此经常采用将微裂纹放置于与各向异性等效的各向同性基岩微元体的背景中来求附加柔度矩阵ΔSijkl的近似办法。下面给出给定各向异性矩阵的最佳各向同性近似体的体积模量K*和剪切模量G*的表达式为:
(22)
层状岩体的弹性参数常采用横观各向同性柔度矩阵,关于该矩阵分量的表达,可参见相关文献,本文不再赘述。如果选择x3轴为对称轴,则该矩阵涵盖了初始微裂纹参数α1=α2的几个取向分布,如微裂纹平面方向都近似平行或者微裂纹法向在x1Ox2平面上的取向服从随机分布。
4 以α为损伤矢量的损伤演化方程
Krajcinovic[10]基于不可逆热力学框架,在Kachanov的损伤理论基础上发展了矢量损伤理论,该方法只要定耗散势函数F的具体形式,就可以独立建立每一个损伤变量的演化方程。
Krajcinovic定义损伤矢量ω=ωin,式中ωi表示法向矢量为n的任意横截面内的缺陷密度。又由上文的讨论可得,对于含扁平微裂纹的基岩微元体,有
ω=α。
(23)
其中,ωi=ρi=αi。因此可以以微裂纹参数α作为损伤矢量来描述损伤的演化过程。
将微裂纹的扩展和滑移看作从一种状态的映射到另一状态的映射,考虑非线性弹性理论和损伤扩展的运动学方程,则可得
(24)
式中:eijk为一置换张量;dαi=αNdΩNN。继而需要建立描述损伤演化的张量dΩNN与应变增量dεij之间的关系,这里采用损伤面的概念。
所谓损伤面,就是应变空间中的一个曲面,该面上各点对应的损伤值相等。损伤面由一个状态变量和一个内变量构成的函数f=f(ε,α,T)来描述,可由实验确定,在缺少实验数据的情况下可以假设损伤面的一般形状,可以推测:
式中:εNN、εNT分别表示局部坐标系(n,t)中垂直于和正切于扁平状微裂纹的应变,星号表示损伤面上的值。
假设损伤速率垂直于损伤面,则有
(27)
式中:G(ε,α,T)是由状态变量和内变量构成的非负的标量函数;κ为一标量因子,其定义为

(28)
由一致性条件df=0可得
联立式dαN=αNdΩNN及式(27)、式(29)可得G(ε,α,T)的表达式为
(30)
至此,便导出了以微裂纹密度二阶张量α为损伤矢量的损伤演化方程,只要知道损伤函数f的表达式,就可以独立建立α3个特征值方向的损伤演化规律。
5 编程实现
根据相关研究资料,取损伤面函数为双曲函数,联想Mohr-Coulomb准则,将表达式定为
(31)
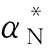
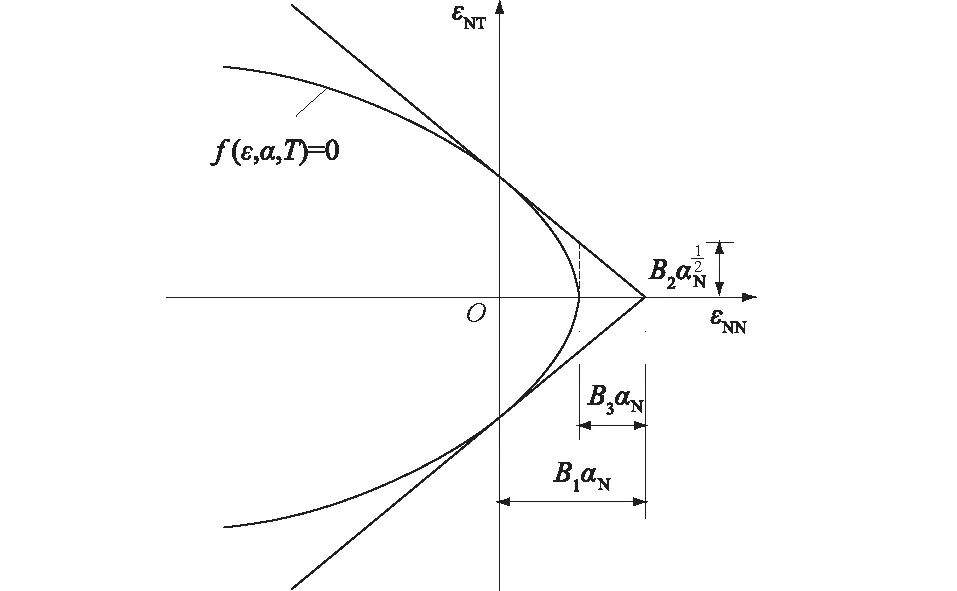
图1 应变空间中的损伤面Fig.1 Damage surface in strain space
由一致性条件可得
(32)
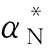
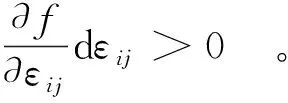
(33)
层状岩体中,假设微裂纹均为圆形裂纹。取α的3个特征值[α1,α2,α3]的方向分别与表征层状岩体产状的局部坐标系Ox′y′z′一致,假设z′轴垂直于岩层面,与α3方向一致,则对于层状岩体的初始状态,有α1=α2。于是可在局部坐标系中得出应变场改变时由3个特征值分别表达的损伤破坏方程。
借助FLAC3D平台,以C++语言进行编程,进行“层状岩体损伤破坏本构模型”的二次开发。计算流程如图2所示。
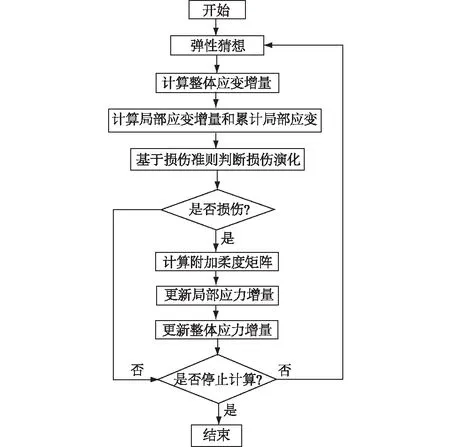
图2 数值模型计算流程Fig.2 Flowchart of numerical calculation of the model
6 试验验证
由于直接采用单轴拉伸法测量岩体的抗拉强度存在一定困难,因此目前应用最广泛的岩体抗拉强度测试方法为巴西圆盘劈裂试验。国内外许多学者采用巴西圆盘劈裂法,从室内试验和数值模拟两方面对层状岩体力学行为的各向异性进行了研究,分析比较了层状岩体在不同的岩性、产状、厚径比等条件下的力学机制及破裂渐进过程。
刘运思等[14]采用巴西圆盘劈裂法系统研究了板岩在不同产状下的破裂渐进过程,本文采用上述二次开发本构模型,对其研究的板岩试样破坏过程进行了巴西圆盘数值模拟。圆盘模型尺寸为50 cm(直径)×25 cm(厚度),共剖分10 120个单元,如图3所示。数值试验采用的物理力学参数如表1所示。
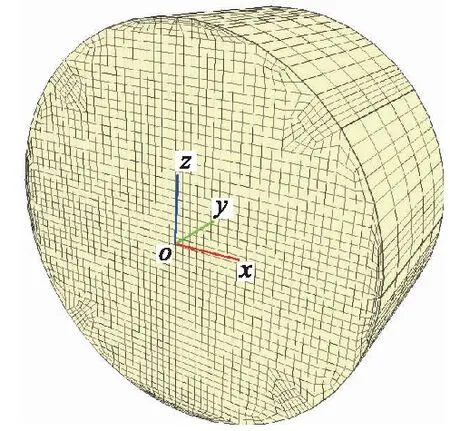
图3 数值模型Fig.3 Numerical model
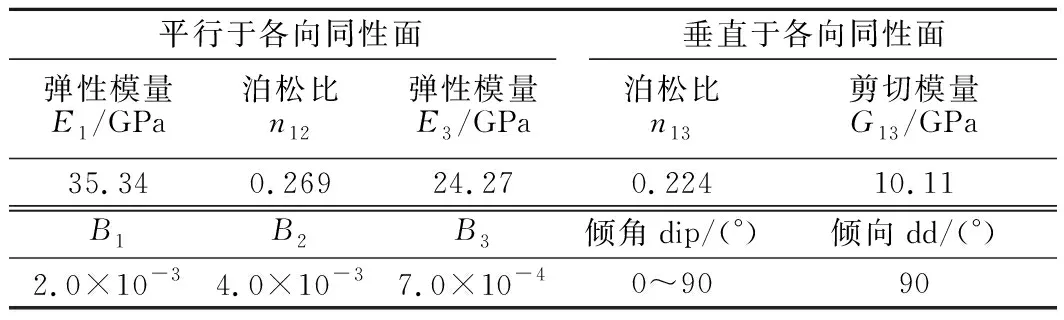
表1 板岩岩体物理力学参数Table 1 Physical and mechanical parameters of slate
本文采用损伤矢量α的模detP来量度三维损伤的累计及岩体破裂的渐进过程,表达式为
(34)
谢和平等[12]的研究表明,岩体破坏时损伤因子的值约为0.20。本文假设detP>0.20时单元损伤破坏,宏观破裂面贯通该单元。在圆盘的顶部和底部逐级施加z向荷载,直至损伤破坏单元贯穿数值模型。根据计算过程中单元损伤破坏的前后顺序,得出岩体的破裂面扩展过程。不同产状的层状岩体损伤云图及破裂面扩展计算结果如图4所示。
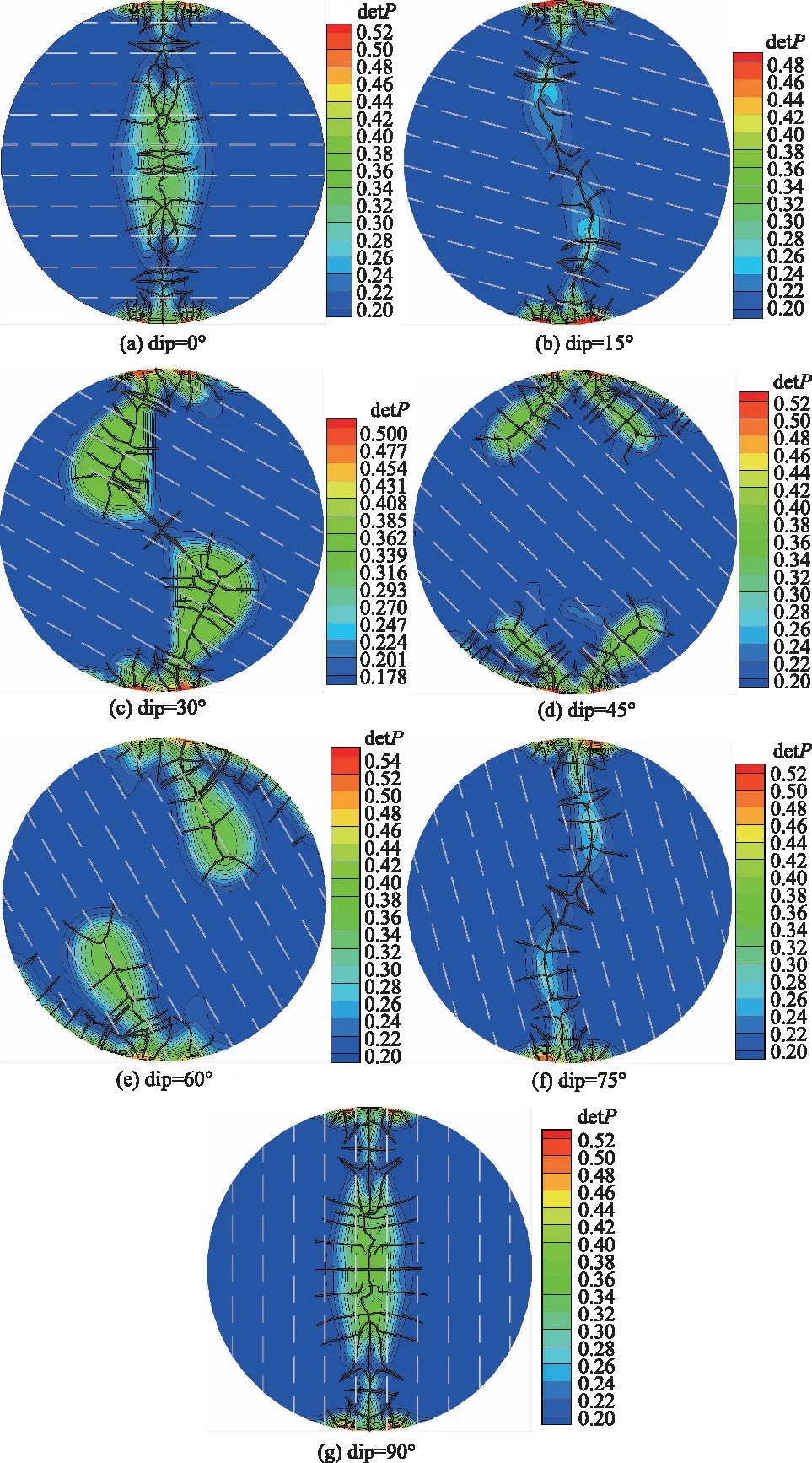
图4 不同倾角的岩体损伤云图及主破裂面扩展(dd=90°)Fig.4 Damage contours and main fracture expansion of rock mass with different dip angles
一般来说,岩体单元损伤值越大,则该单元越早出现损伤破坏,因此岩体损伤等值线的梯度下降方向表征破裂面的扩展方向。由图4可以得出,不同倾角的层状岩体在巴西圆盘劈裂试验中的起裂点及主破裂面扩展过程为:
(1)层理倾角0°时,试样主破裂面从加载点起裂,接着试样中心岩体单元发生破裂,最后主破裂面沿着垂直于层理面的方向贯通。
(2)层理倾角15°、30°时,试样主破裂面从加载点起裂,然后沿着垂直于层理面的方向扩展,最后在试样中心沿着层理面的方向贯通。
(3)层理倾角45°、60°时,试样主破裂面从加载点起裂,然后沿着层理面的方向扩展贯通。
(4)层理倾角75°时,试样主破裂面从加载点起裂,然后沿着层理面的方向扩展,最后在试样中心沿着垂直于层理面的方向贯通。
(5)层理倾角90°时,试样主破裂面从加载点起裂,接着试样中心岩体单元发生破裂,最后主破裂面沿着层理面的方向贯通。
(6)层理倾角0°、90°时,主破裂面为通过加载中心和试样中心的近似平面,满足巴西圆盘劈裂试验力学模型的假定,测出的抗拉强度符合公式计算结果;层理倾角为其他角度时,主破裂面为偏离了加载中心的曲面,此时力学模型与计算公式不一致,测出的抗拉强度不够准确。
对比文献[15-19]可知,本文数值试验得出的破裂面扩展过程与文献室内试验结果吻合较好,因此,本文二次开发的本构模型能够较好地预测层状岩体渐进破坏的各向异性特性。
7 结 论
基于细观损伤力学理论,运用体积平均化的方法,以二阶张量α作为表征微裂纹密度的参数,推导了微裂纹对岩体弹性柔度矩阵的贡献,在非相互作用近似的框架下,建立了层状岩体的有效弹性柔度矩阵。同时,基于前人的矢量损伤理论,导出了以α为损伤矢量的损伤破坏方程,假设了损伤函数f的表达式,建立了α3个特征值方向独立的损伤破坏规律。并借助FLAC3D平台,进行了“层状岩体损伤破坏本构模型”的二次开发。
采用二次开发本构模型,对层状岩体的破坏过程进行了巴西圆盘数值模拟。结果表明:在层理面不同倾角下,岩体试样的破裂面均从加载点起裂,但破裂面扩展过程随倾角改变而不同;与室内试验结果对比可知,本文二次开发的本构模型能够较好地预测层状岩体渐进破坏的各向异性特性。
本文提出的“层状岩体损伤破坏本构模型”为模拟不同产状下层状岩体的渐进破坏过程提供了一种新的方法。但是层状岩体的损伤破坏过程非常复杂,文中的本构模型是在一系列假设的基础上推导得出的,仍需在岩体中不规则形状的微裂纹扩展、考虑损伤的岩体断裂、岩体的层理面特性等方面作出更深入细致的研究,以加深对层状岩体损伤破坏的认识。
