基于Copula函数的叶尔羌河水沙丰枯遭遇研究
2022-03-02居金浩娜扎凯提托乎提卫仁娟
居金浩,彭 亮, 2,何 英, 2,娜扎凯提·托乎提,卫仁娟
(1.新疆农业大学 水利与土木工程学院,乌鲁木齐 830052; 2.新疆水利工程安全与水灾害防治重点实验室,乌鲁木齐 830052; 3.四川大学 水利水电学院 水力学与山区河流开发保护国家重点实验室,成都 610065;4.四川水利职业技术学院,成都 611230)
1 研究背景
径流与泥沙的关系涉及到水土资源规划与管理、水利基础设施建设与运行以及流域系统演化,一直以来都是水科学领域一个十分热点的题目[1-2]。联合国政府间气候变化专门委员会第五次报告指出,20世纪80年代至21世纪10年代可能是北半球上千年来气温最高的30 a。全球气候变化冲击了原本平稳的水文循环系统,导致全球范围内极端灾害(如干旱、洪水和高温热浪等)频繁发生[3],对社会经济、生态环境等造成重大影响,水文循环系统中活跃的因子径流和输沙也发生了明显改变[4-5]。诸多学者针对流域内水沙展开研究,徐金鑫等[6]分析了丹江流域径流和泥沙单一要素在空间上的分布及在时间上的发展趋势;也有学者分析了径流和输沙对气候变暖和人类活动(水库建设和土地利用类型改变等)的响应[7-8],并参照未来情景模式数据探究径流和输沙各自未来的发展状况[9-11]。以上的研究手段都将水沙割裂开来进行分析,而水沙二者之间具有一定的某种相关关系,故对年径流量和年输沙量两变量分开单独进行研究而分析所得的结论是不够客观的。
近年来, 在金融领域广泛应用的Copula理论广泛应用于水文领域。 Copula理论的优势是其不需要变量的分布严格相同, 不一致的边缘分布也可以通过Copula函数构建联合分布模型, 而在转换过程中不会造成变量中的信息失真[12]。 周念清等[13]采用洞庭湖流域水沙2个系列的数据, 构建径流量和输沙量Copula二维联合分布模型, 探究洞庭湖流域水沙丰枯遭遇概率, 研究结果显示洞庭湖流域水沙运动与水沙丰枯遭遇概率有密切的联系。 郭爱军等[14]采用滑动相关系数法与双累积曲线法相互对比得出水沙关系的突变点, 然后基于Copula函数建立水沙联合分布模型, 发现变异后时段水沙均值均减少, 但变异前后水沙丰枯同步概率一直占主导地位, 变异后时段水沙丰枯异步概率增加。 诸多研究[15-17]均显示构建Copula水沙二维联合分布模型能够较好地表达水沙二者之间的相关关系。
本文基于Copula函数建立水沙二维联合分布模型,探究叶尔羌河径流量和输沙量丰枯遭遇频率,并分析水沙两者的相互作用关系。本文研究成果可为叶尔羌河流域水沙运行调度与管理提供理论依据,并为流域的防洪减灾提供技术参考。
2 流域概况
叶尔羌河是塔里木河的重要源流之一,起源于喀喇昆仑山北坡,河源至河口全长1 078 km,流域地理位置介于74°28′E—80°54′E、34°50′N—40°31′N之间。叶尔羌河灌区处于西北干旱和半干旱气候区,排名全国第四、新疆第一大灌区。叶尔羌河卡群站实测多年平均年径流量67.10亿m3,年径流量变差系数0.18;多年平均悬移质输沙量3 028万 t,最大日含沙量698 kg/m3(1998年6月3日),多年平均最大月含沙量6.41 kg/m3(8月份)。
叶尔羌河上游地区气温较低,冰冻期较长[18],降水稀少,造成地面植被稀疏和土壤水土保持能力不足,故河道泥沙含量较高,水沙问题突出,给灌区内水生态修复和流域防洪减灾等工作造成很大影响。
3 资料来源与研究方法
3.1 资料来源
本文研究数据采用叶尔羌河流域卡群水文站1954—2015年、库鲁克栏干站1979—2015年径流量和输沙量数据,均来自喀什水文水资源勘测局。水文站具体位置见图1。
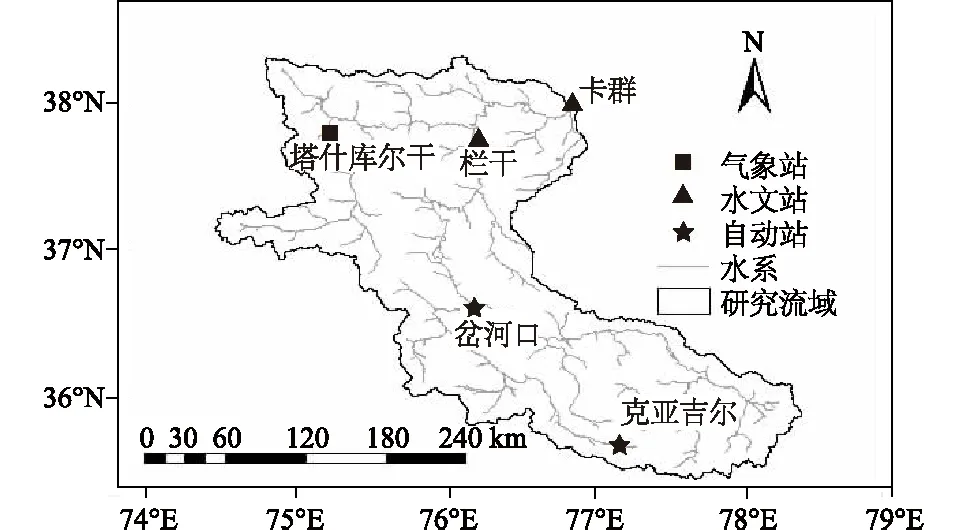
图1 叶尔羌河流域水系Fig.1 Water system in Yarkant River Basin and locations of hydrological stations
3.2 模比系数差积曲线法

(1)
(2)
(3)
3.3 滑动t检验法
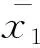
(4)
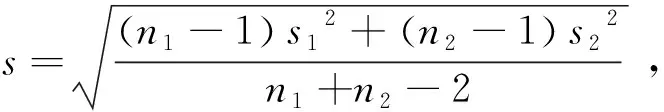
根据显著性水平α和t分布表查得临界值tα,若|ti|>tα,则判定出现了变异。
3.4 滑动相关系数法
设有径流X=(x1,x2,…,xn)和输沙Y=(y1,y2,…,yn)2个序列,确定窗口大小为m年,时间长度为1 a的滑动,首先计算第1个窗口X1=(x1,x2,…,xm)和Y1=(y1,y2,…,ym)2个子序列的Kendall相关系数r1,然后计算第2个窗口X2=(x2,x3,…,xm+1)和Y2=(y2,y3,…,ym+1)2个子序列的Kendall相关系数r2,依次得出其后子序列的Kendall值,直至得到Xn-m+1=(xn-m+1,xn-m+2,…,xn)和Yn-m+1=(Yn-m+1,yn-m+2,…,yn)2个子序列的Kendall值rn,绘制相关系数-年份曲线。Kendall相关系数是反映X和Y两个序列的相关程度,故绘制的相关系数-年份曲线能很好地体现X和Y两个序列在不同时段的相关系数。基于此,我们可以认为曲线上明显的转折点即为X和Y的变异点。
3.5 二维Copula函数
Copula理论在1959年Sklar[19]提出之后一直局限在理论创新而没有参与到各个行业的实践应用中。直到Embrechts等[20]首次将其应用于金融领域,并取得了较好结果,随后也在水文领域广泛应用。Copula是定义域在[0,1]上的多维联合分布函数,通过Copula可联接分布不一致的变量建立多元联合分布模型。以二元Copula举例:假设H为二维联合分布函数,F和G为其边缘分布,那么有Copula函数C使得
H(x,y)=Cθ(F(x),G(y)) 。
(5)
式中θ为Copula函数的参数。
3.6 Copula的参数估算与优度检验
3.6.1 Copula参数估算
本文采取非参数估计法计算Copula函数中的参数,通过θ与 Kendall 系数τ之间的关系求解。Copula参数θ和Kendall系数τ具体的对应关系(θ对应T,α对应τ)见表1。

表1 函数类型与参数Table 1 Types and parameters of functions
3.6.2 Copula优度检验
各类Copula都拥有各自的特点,因此需要选择拟合度较高的Copula函数,以期提高水沙二维联合分布模型的精确性。本文选用AIC、OLS和图形分析等方法进行Copula模型评价。
(1)AIC又称赤池信息量准则。AIC基于熵理论而建立,可以评价所估计模型的复杂度和此模型对数据拟合的情况,AIC值较大说明模型的拟合度较差。AIC可以表示为
AIC=2K-lnL。
(6)
式中:K是参数的数量;L是似然函数。
(2)OLS又称离差平方和最小准则。通过离差平方和最小准则评估Copula函数的拟合情况,选取OLS最小值作为最优Copula。计算公式为
(7)
式中Ci和Pi分别为理论累积概率和经验累积概率。
(3)Genest-Rivest图形分析法是Genest和Rivest提出的一种评价Copula函数拟合效果的方法,分别计算理论估计值Kc(t)和Ke(t),然后点绘Kc(t)和Ke(t)关系图,如果图上的点都落在45°对角线上,那么表明Kc(t)和Ke(t)完全相等,即Copula函数拟合得很好。
4 结果与分析
4.1 水沙年际变化
在气候变暖和人类活动加剧两方面影响下,流域水沙均发生显著变化[21-22]。叶尔羌河卡群站、库鲁克栏干站水沙多年丰枯交替情况见图2。对比卡群站和库鲁克栏干站水沙模比系数差积曲线,可以发现两站年径流量和年输沙量的丰枯遭遇总体上同步,均以1993年为节点,从趋于枯水(枯沙)状态转变为一个大的丰水期(丰沙期)。
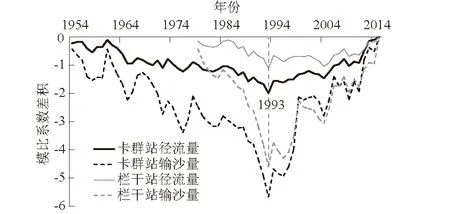
图2 模比系数差积曲线Fig.2 Curves of product of difference of modulus coefficient
卡群站1954—1992年为年径流量、年输沙量下降的枯水时段,其模比差积曲线整体呈下降趋势, 1993—2015年曲线陡升,是一个显著的丰水(丰沙)期。库鲁克栏干站1979—1992年为年径流量、年输沙量下降的枯水(枯沙)时段,其模比差积曲线整体呈下降趋势, 1993—2015年曲线陡升,是一个显著的丰水(丰沙)期。在两站的枯水(枯沙)期和丰水(丰沙)期,输沙量的变化幅度远显著于径流量的变化幅度。
为了验证模比系数差积曲线判别水沙序列突变点的精准度,运用滑动t检验法再次对两站水沙序列的突变点进行分析。采取子序列长度为8,在α=0.05的显著性水平下的分析结果见图3。由图3可见,卡群站和库鲁克栏干站水沙均在1993年发生突变,对比模比系数差积曲线分析的结果,确定1993年为两站水沙序列的变异点。
给予大剂量LPS刺激后,Kupffer细胞胞质组织蛋白酶B活性检测结果显示:分别与各自对照组(NS组)比较,WT LPS组与TLR4-/-LPS组Kupffer细胞胞质中组织蛋白酶B活性显著增加(P<0.05,图4);WT LPS组与TLR4-/-LPS组相比,Kupffer细胞胞质中组织蛋白酶B活性增加程度无明显差异(图4)。表明TLR4缺失并不影响大剂量LPS刺激下胞质中组织蛋白酶B活性的增加。
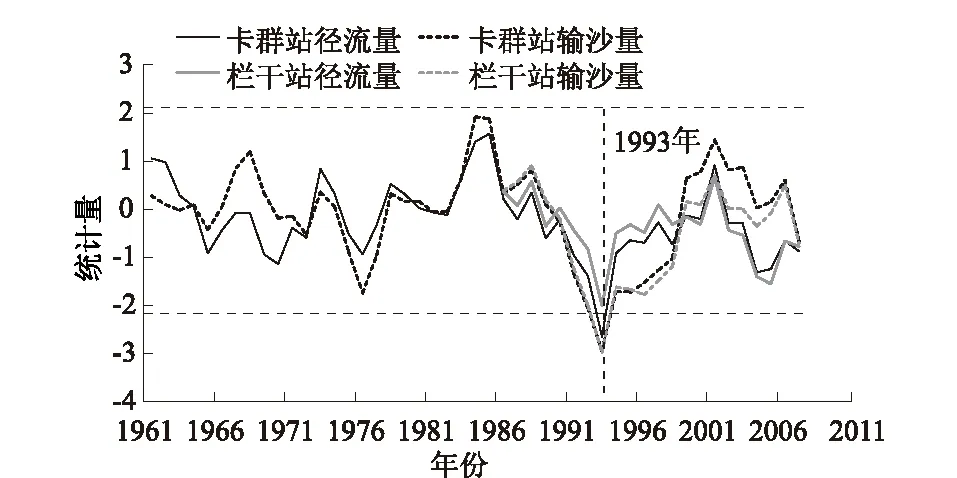
图3 滑动t检验结果Fig.3 Result of moving t-test
4.2 水沙关系变异点诊断
为确定水沙关系的突变点,采用滑动相关系数法对叶尔羌河流域卡群站的年径流量和年输沙量进行窗口大小为1 a、时间长度为4 a的滑动,削减异常年份对水沙产生的变化。图4为基于滑动相关系数法检验的叶尔羌河卡群站水沙关系突变点。由图4可知1979年、1993年是卡群站水沙相关关系较为明显的转变点。卡群站1979年之前平均滑动相关系数为0.70,1979—1993年平均滑动相关系数为0.53,1993年之后平均滑动相关系数为0.69。
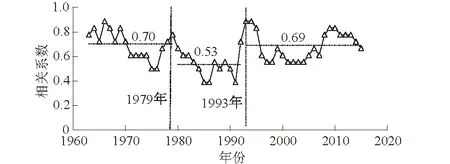
图4 基于滑动相关系数的水沙关系变异点判断Fig.4 Points of abrupt changes in the relation between water and sediment by moving correlation analysis
流域水沙序列突变是由气候和地表过程等多种因素综合作用造成的。自20世纪90年代起,研究区年降水量呈现平缓增加趋势[23],并未有突跃式的增长,且研究区降水稀少,雨雪对径流补给仅占多年平均径流量的13.4%,故降水变化对径流的突变影响较小。研究区冰川融雪对径流的补给较大,故温度变化对其水沙序列影响显著[24]。有研究[25]表明叶尔羌河流域的气温在50多年来有明显的上升趋势,气温上升均为突变产生,且研究区内多地气温突变均发生在20世纪90年代。也有学者指出1993年前后新疆地区的夏季零度层高度显著上升,雪线上移坡面产流量增加的同时冻土退化。一方面径流侵蚀能力增强,另一方面下垫面抗侵蚀能力减弱,最终造成水土流失加剧,河道泥沙量增加。
4.3 变化环境前后水沙关系特征对比分析
综合考虑滑动相关系数法、双累积曲线法的分析结论,以及人类活动加剧和气候变暖对叶尔羌河河流域水沙关系的影响,本文确定水沙关系于1993年变异,水沙序列划分为变异前(1954—1992年)与变异后(1993—2015年)2个阶段,采用线性矩法统计卡群站水沙频率分布函数的特征值,见表2。
由表2可知,年径流量在水沙关系变异前后有10%左右的增长,年输沙量变异后(1993—2015年)较变异前(1954—1992年)有更为明显的增长,变幅大约为40%;年径流量和年输沙量的离势系数Cv在变异前后均未发生明显变化,表明径流序列和输沙序列的波动在水沙关系变异前后无明显变化,输沙序列值的变化程度强于径流序列值;变异前(1954—1992年)年径流量和年输沙量的偏态系数Cs值较变异后(1993—2015年)变化幅度分别为-67.00%和-35.77%,表明变异后的年径流量和年输沙序列较变异前稳定。

表2 水沙关系变异前后年径流量和年输沙量特征值与频率分析Table 2 Characteristic values and frequencies of runoff and sediment before and after abrupt change
深入分析年径流量和年输沙量在不同频率下的特征值于变异点前后的变化。水沙关系变异后(1993—2015年)较水沙关系变异前(1954—1992年)年径流量呈现增长趋势,增长幅度大约为10%;年输沙量在1%≤P≤90%时均呈现增加趋势,且增幅较大,除P=90%外,其余特征值下增幅都达到了40%以上。
4.4 变化环境前后水沙丰枯遭遇分析
4.4.1 联合分布模型的建立
根据上文水沙关系变异前后特征值与频率分析结论,应用频率法定义9种水沙组合类型,见表3。

表3 水沙组合类型Table 3 Types of runoff and sediment combinations

图5 变异前后Kc-Ke关系Fig.5 Coherence comparisons between empirical cumulative frequency and theoretical cumulative frequency before and after variation
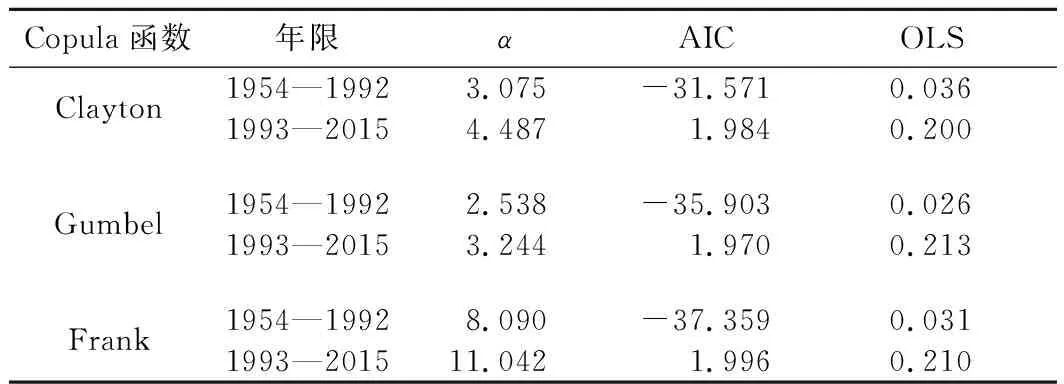
表4 Copula函数参数估计结果及拟合优度检验Table 4 Parameters of Copula functions and evaluation result of goodness of fit
由表4可知,变异前(1954—1992年)AIC检验最优的是Frank Copula,OLS检验最优的是Gumbel Copula,图形分析法检验最优的是Gumbel Copula;变异后(1993—2015年)AIC检验最优的是Gumbel Copula,OLS检验最优的是Clayton Copula,图形分析法检验最优的是Gumbel Copula。故叶尔羌河流域变异前和变异后的水沙关系耦合模型均选择Gumbel Copula函数,即
H(u,v)=exp{-[(-lnu)×2.581 2+(-lnv)×2.581 2]1/2.581 2} 。
(8)
式中u、v分别代表2个边缘函数。
4.4.2 水沙丰枯遭遇结果
叶尔羌河流域的水沙丰枯遭遇结果见表5。 由表5可以看出:①水沙关系突变前后水沙丰枯同步概率均大于丰枯异步概率,变异点后水沙的丰枯同步概率更高,且同平概率最大;②流域水沙遭遇的丰枯异步概率中的水丰沙枯与水枯沙丰、水平沙枯与水枯沙平、水丰沙平与水平沙丰遭遇概率相近。水丰沙枯和水枯沙丰遭遇概率为0,表示这2种类型遭遇的概率极低;③环境变化后(1993—2015年)水沙丰枯同步概率为82.61%,相对环境变化前增加23.64%,丰枯异步概率减小,有20.62%。变化环境前后水沙同丰组合类型所占的比例变化幅度较大,增加幅度为22.74%。变异前年不同遭遇组合发生概率变化范围为0~38.46%,变异后年不同遭遇组合发生概率变化范围为0~43.48%。

表5 变异前后水沙丰枯遭遇概率Table 5 Probabilities of the combinations of runoff and sediment before and after abrupt change
图6为流域变异前概率密度函数图和概率分布函数图,图7为流域水沙关系变异后(1993—2015年)概率密度函数图和概率分布函数图。从图中可以查出流域水沙各种遭遇组合的概率,为流域水沙治理提供决策支持。
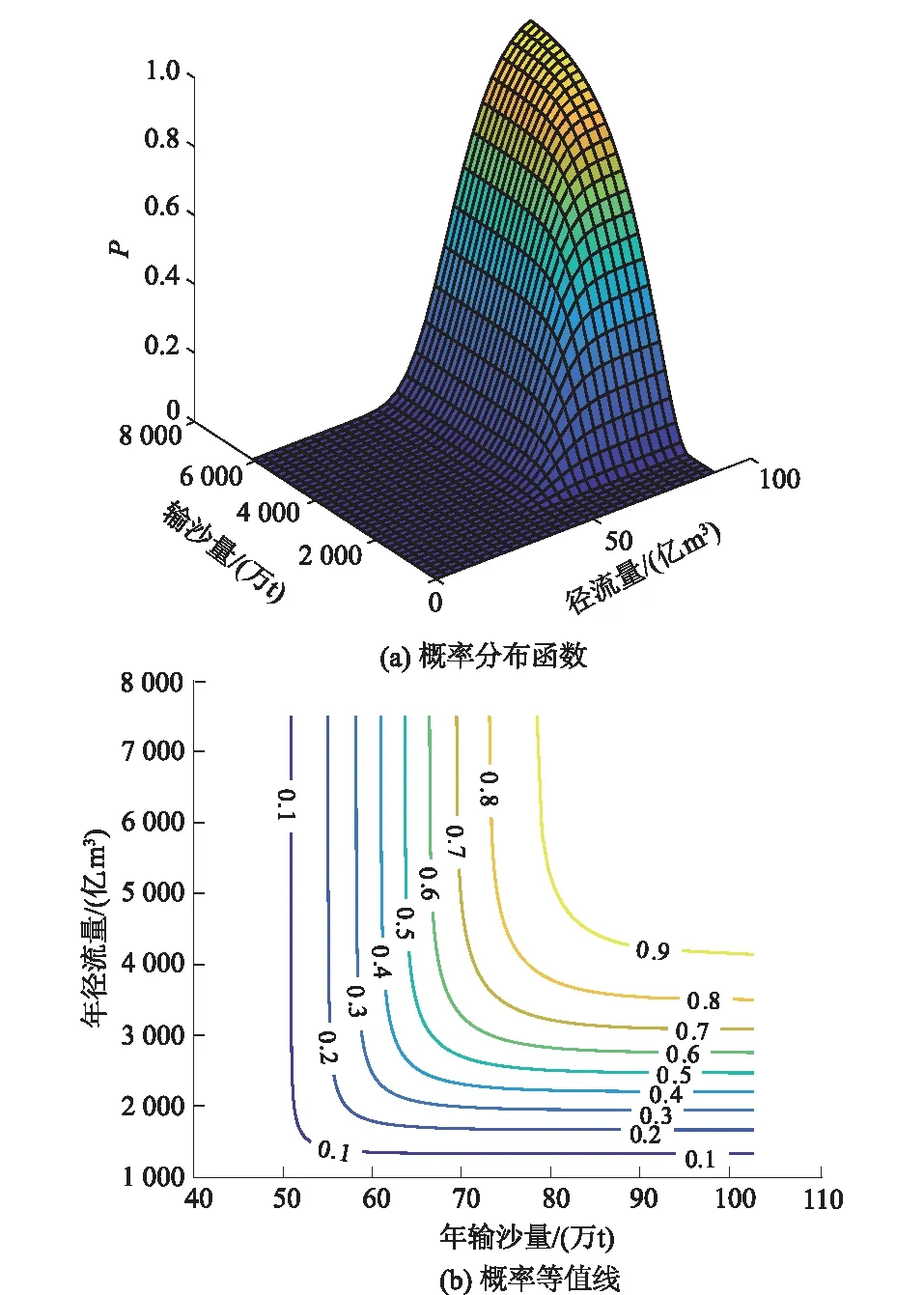
图6 1954—1992年水沙联合概率分布函数和等值线Fig.6 Joint probability distribution of runoff and sediment and the isolines during 1954-1992

图7 1993—2015年水沙联合概率分布函数和等值线Fig.7 Joint probability distribution of runoff and sediment and the isolines during 1993-2015
5 结 论
基于叶尔羌河卡群站1954—2015年、栏杆站1979—2015年径流量和年输沙量,分析叶尔羌河水沙相关程度的变化情况,进一步构建不同时段下不同类型的Copula水沙模型,分析叶尔羌河流域水沙丰枯遭遇状况,得出以下结论:
(1)叶尔羌河年径流量与年输沙量均呈现增长趋势,采用模比系数差积曲线图法和滑动t检验法均诊断出径流和输沙序列分别在1993年发生变异,尽管水沙均呈现增加趋势,但在突变点后输沙量的增加趋势远显著于径流量的增加趋势。
(2)通过滑动相关系数法判断出叶尔羌河流域水沙关系同样是在 1993年发生变异,气候变暖引起融雪量的增加可能是导致水沙序列突变的重要因素。
(3)水沙关系变异前后的水沙联合分布相差较大,设计概率下特征值变化较大,P≤90%时径流量、输沙量均增加,输沙增加趋势更为显著;P>90%时,径流量增加,输沙量减少。
(4)两时段中丰枯同步的概率都大于丰枯异步概率,“水丰沙枯”和“水枯沙丰”2种组合概率为0。变异前(1954—1992年)丰枯遭遇概率(38.46%)最高的类型是同平,水枯沙平(15.38%)次之;变异后(1993—2015年)遭遇概率(43.48%)最高的类型是同平,同丰(30.43%)次之,变异后的水沙丰枯同步概率比水沙关系变异前的丰枯同步概率高23.64%。
