一种模拟黏土心墙坝漫顶溃决的水沙耦合数学模型
2022-03-02王亚林
王 廷,王亚林
(三峡大学 水利与环境学院,湖北 宜昌 443002)
1 研究背景
黏土心墙坝具有土石坝就地取材,对地形、地质适应能力强等特点,与均质坝和斜墙坝相比,其坝坡陡,相对工程量小,基础防渗线短,抗震性能好,因此长期以来黏土心墙坝都是坝工界设计人员优先选择的一种坝型。在世界范围内黏土心墙坝数量众多,建设规模也不断突破,目前在建和已建的超高黏土心墙坝有双江口黏土心墙坝(314.0 m),努列克黏土心墙坝(300.0 m)以及两河口黏土心墙坝(295.0 m)等。这些工程在带来巨大的经济效益与社会效益的同时也存在着溃坝风险。据统计1954—2014年我国的土质心墙坝溃坝数量达到183座,造成了大量的人员伤亡和财产损失,其中漫顶导致的溃坝超过50%[1]。因此,为了提高黏土心墙坝的安全控制水平,减轻黏土心墙坝漫顶溃决损失,需要对黏土心墙坝的漫顶溃决机理、溃口发展过程、溃口洪水流量过程、洪水演进过程以及评估溃坝风险[2]进行深入研究。
国内外学者通过黏土心墙坝漫顶溃决试验发现[3-4]:随着下游坝壳逐渐被冲蚀,心墙在上游动水压力和土压力的作用下,发生滑移或倾倒破坏(如图1、图2所示,其中Fa为坝壳作用在心墙上的土压力,Fw为库水作用在心墙上的水压力,Fsb为沿破坏面底部作用的摩擦力,Fcb为沿破坏面底部的黏结力),导致溃口流量迅速增加,冲蚀加剧,直至大坝完全溃决。
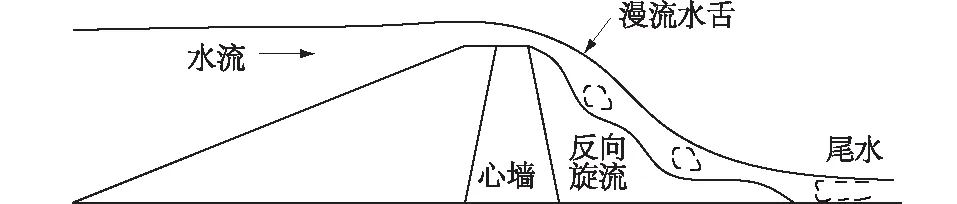
图1 水流淘刷下游坝壳示意图Fig.1 Schematic diagram of scouring and breaking of downstream dam shell
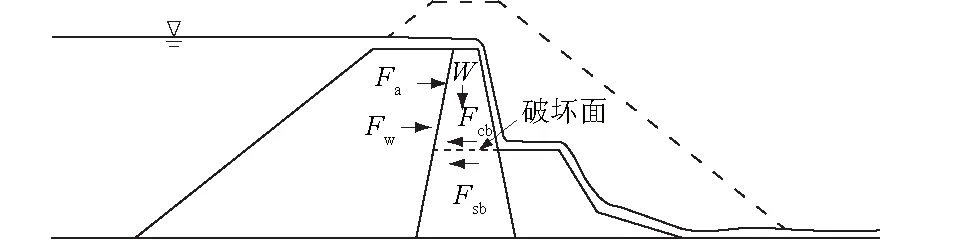
图2 黏土心墙滑动失稳坝示意图Fig.2 Schematic diagram of clay core sliding
根据这一溃决机理,任强等[5](2010)建立的数学模型能够较好地描述心墙失稳所引起的溃口间歇性增大现象。陈生水等[3](2011)提出了漫坝水流对下游坝壳料冲蚀的经验公式。钟启明等[6](2017)模拟了心墙倾倒破坏和剪切破坏。这些成果对于溃口发展的模拟研究均颇有意义,然而上述模型中水流计算采用的一维平均流速很难体现溃口水流复杂的水力特性,进而无法精确模拟下游坝壳的冲蚀过程。而下游坝壳冲蚀过程对于心墙失稳破坏具有重要影响。
为了实现对溃口复杂冲蚀过程的模拟,本文建立了黏土心墙坝漫顶溃决的动床水沙耦合数学模型。其中水流运动方程采用固液两相湍流方程,并通过PLIC-VOF法(分段线性界面重构-流体体积法)捕捉洪水自由液面的位置,精确预测洪水运动过程。对于坝壳非黏性沙输移的计算则采用了不饱和全沙输移方程。黏土心墙的破坏通过剪切力进行判断。
2 数学模型
2.1 水-沙耦合的固液两相湍流方程
水动力学模型采用了固液两相湍流方程,可以较好地反映泥沙运移与床面变形对于水流运动的影响。
连续方程:
(1)
动量方程:
(2)
悬沙对流扩散方程:
流体湍流动能k方程:
(4)
其中:
μmt=ρmCμk2/ε。
式中:t为时间;ρm为混合物密度;um,i为混合物在xi方向上的流速;um,j为混合物在xj方向上的流速;αp为泥沙体积分数;δj3为重力方向Kronecker delta符号;ω为泥沙沉降速度;μm为混合流体黏性系数;p为动水压强;νmt为湍涡黏度;σp为临界正应力;Cμ和σk均为系数,取Cμ=0.09,σk=1.0;ε为动能耗散率。
流体湍流动能耗散率ε方程:
式中:C1、C2、σε均为系数,C1=1.44,C2=1.92,σε=1.3。
考虑含沙量变化的混合流体黏性系数为
(6)
式中:αs为泥沙体积分数;αcr为临界底沙体积分数;αco为给定的常数;μf为清水有效黏性系数。
2.2 自由面处理
自由面重构采用PLIC-VOF法,F为流体体积函数,满足输运方程,即
(7)
PLIC-VOF法采用斜线段来模拟单个网格内的交界面。该方法主要涉及两方面的问题[7]:
(1)已知网格体积分数F值条件下,计算自由表面的法向矢量n,从而精确重构自由表面。
(2)相邻网格内的对流体积计算。
2.3 泥沙侵蚀
泥沙剪应力τb为
(8)
式中:τbo,i,j为编号网格剪应力值;τbo,i±1,j为i方向相邻网格剪应力值;τbo,i,j±1为j方向相邻网格剪应力值;|xn|、|zn|分别为底沙表面的单位法向向量在x、z方向的投影。
单个网格的剪应力为
(9)
其中:
(10)
μtot=μm+μmt。
(11)
泥沙减少量Cremoved为
Cremoved=αcrρsLtot。
(12)
式中:ρs为泥沙密度;Ltot为泥沙通量。Ltot可通过下式计算,即
(13)
式中:Δt为时间步长;τc为临界剪应力。τc可表述为
τc=θcgi(ρs-ρf)d50。
(14)
式中:gi为重力加速度;d50为中值粒径;ρf为流体密度;θc为校正斜率。
θc可以表述为
式中:η为休止角;ξ为河床坡度;θc,0为斜率初始值。
2.4 心墙滑移
流体计算过程中,黏土心墙作为固壁边界,采用基于离散力的浸入边界法来模拟。垂直边界的速度满足对流方程[8]为
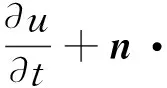
(16)
式中u为垂直边界速度。
完成每一步的流体计算,需进行心墙结构受力计算。心墙的破坏面位于坝壳垂向下切深度的水平面,计算破坏面上每个节点的法相应力σ和剪切应力τ,通过沿破坏面积分计算出整个破坏面上总的滑动力和抗滑力,心墙发生滑移破坏[9]时,作用在心墙上的力满足式(17),即
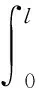
(17)
式中:c为黏土心墙的内聚力;φ为黏土心墙的内摩擦角;τxy为滑移面剪应力。
数值计算采用结构网格和控制体积法对计算区域进行离散,详细计算过程可以参看文献[10]。
3 数值模拟
数值计算的模型尺寸,材料参数与开展的室内验证试验一致,坝高0.6 m,顶宽0.1 m,上下游坝坡坡比1∶2,心墙顶宽0.06 m,心墙坡比1∶0.2。坝壳堆石体含水量2.7%,特征粒径d50=6.5 mm,干重度20.7 kN/m3,无黏聚力,内摩擦角47.8°;心墙含砾黏土含水量6.1%,d50=0.9 mm,干重度19.5 kN/m3,黏聚力36 kPa,内摩擦角24.9°。初始水头0.05 m,试验水流流量0.01 m3/s。
数值模型由160 000个单元网格组成,其中单元尺寸为2 cm×2 cm×4 cm。前、后边界及底面边界均为壁边界,顶面为对称边界。左、右边界分别为流量边界和出流边界。
3.1 数值模拟溃口发展过程
整个溃坝过程可分为以下2个阶段。
(1)逐渐冲蚀阶段。在这一阶段中,一方面水流结构,与下游坝壳的床面形态息息相关,而下游坝壳的床面形态又随着水流结构的变化而不断改变。另一方面随着下游坝壳被冲蚀,心墙下游侧临空面逐渐加大,当心墙发生滑移破坏,将导致下泄流量突增。如图3所示,由于局部扰动引起近壁层流层波动,下游坝坡形成沙纹,沙纹尺度较小,此时坝面起伏幅度不大(图3(a)、图3(b))。随着水流冲蚀,坝面形成与水面波同相位的沙浪形态,这时的坝面沙浪与水面波浪之间有强烈的相互干涉作用(图3(c)—图3(g))。此后,水流在迎水面产生局部水跃,背水面则产生水跌,致使水面波动超过坝面的起伏,形成“陡坎”(图3(h)—图3(l))。“陡坎”逐渐发展,使得坝顶下缘位置心墙临空面逐渐加大,当土压力和水压力的共同作用超过心墙的极限抗剪强度,心墙发生第一次滑移破坏。

图3 溃坝过程逐渐冲蚀阶段Fig.3 Gradual erosion stage
(2)剧烈溃决阶段。如图4所示,心墙发生第一次滑移破坏之后,泄流流量突增,漩涡水流向内剧烈淘刷,引起第二次心墙滑移破坏,流量进一步增大,在达到峰值之后又快速减小,直至溃决结束。
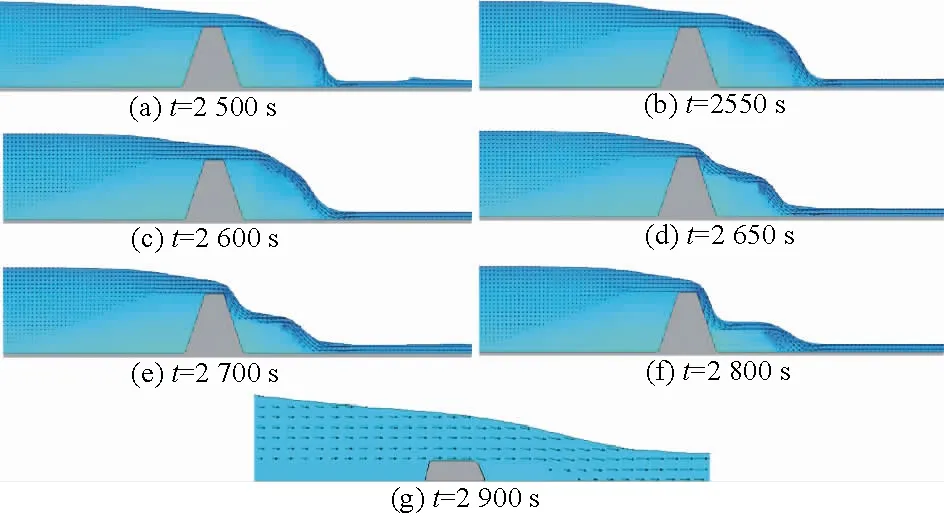
图4 溃坝过程剧烈冲蚀阶段Fig.4 Violent outburst stage
3.2 数值模拟与室内试验溃口流量结果对比
为了验证模拟的精度,开展了室内漫顶溃坝试验。对于正态模型,非黏性土在满足砂砾雷诺数Re*>70的前提下,符合式(18)、式(19),即可满足模型的水流流态相似[11]。
λd=λh=λL,
(18)
λρs=λρ=1 。
(19)
式中:λL为几何比尺;λd为砂粒粒径比尺;λρs为砂粒密度比尺;λh为水深比尺;λρ为水密度比尺。
试验系统工作原理如图5所示,试验系统平面布置示意图如图6所示。试验中使用高清摄像机对溃口发展过程进行记录。粒子图像测速系统采集平均流速,并结合断面形态可以得到溃坝流量。全自动水位激光观测仪,进行水位变化的监测。初始水头为0.05 m,试验水流流量为0.01 m3/s。
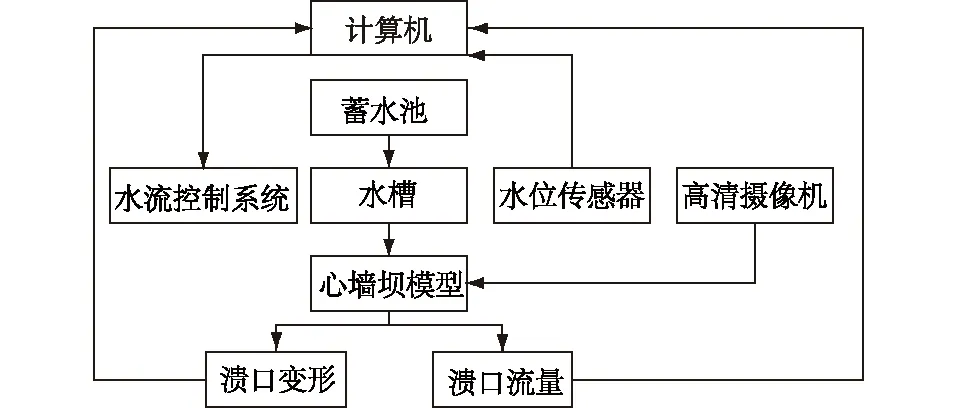
图5 试验系统工作原理Fig.5 Working principle diagram of test system
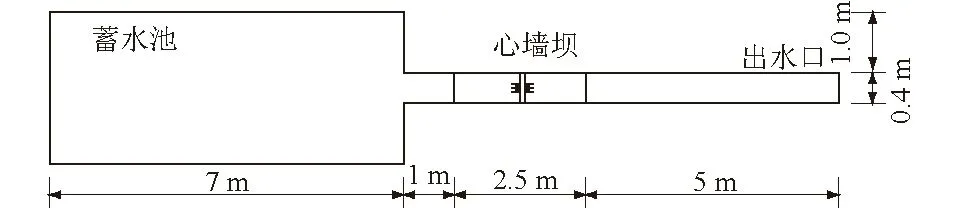
图6 试验系统平面布置示意图Fig.6 Plane layout diagram of test system
根据图7可知,计算与试验中的流量过程线较为接近。第一次心墙滑移导致流量迅速增大的时间点计算值比试验提前42 s,模拟的心墙滑移面较试验高0.03 m。第二次心墙滑移导致流量迅速增大的时间点计算值比试验滞后27 s,模拟的心墙滑移面较试验值低0.05 m。计算值与试验值的溃口峰值流量分别为0.142、0.149 m3/s,数值模拟中峰值流量出现的时间点较试验值推后58 s。
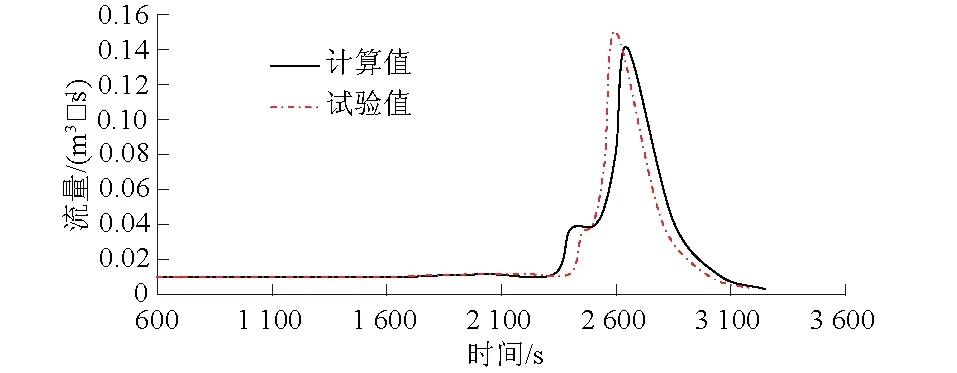
图7 溃口流量过程对比曲线Fig.7 Computed and test discharge curves at the breach
4 结 论
(1)黏土心墙坝在漫顶溃决过程中,溃坝水流冲刷坝壳,坝壳发生变形又反过来影响水流波动。下游坝壳的变化过程为沙纹、沙浪、陡坎3种形态,直到黏土心墙发生失稳滑移破坏,导致溃坝水流突增,大坝进入剧烈溃决阶段。
(2)基于黏土心墙坝的漫顶溃决机理,建立的黏土心墙坝溃坝水沙耦合模型,能够在一定程度上模拟整个黏土心墙坝漫顶溃决过程,经室内水槽试验检验,预测的溃口流量过程与实测值也较为吻合,为研究黏土心墙坝漫顶溃口发展过程提供一种可选工具。
