System identification with binary-valued observations under both denial-of-service attacks and data tampering attacks:the optimality of attack strategy

Jin Guo·Xuebin Wang·Yanling Zhang·Wenchao Xue·Yanlong Zhao

Abstract With the development of wireless communication technology, cyber physical systems are applied in various fields such as industrial production and infrastructure,where lots of information exchange brings cyber security threats to the systems.From the perspective of system identification with binary-valued observations,we study the optimal attack problem when the system is subject to both denial of service attacks and data tampering attacks.The packet loss rate and the data tampering rate caused by the attack is given, and the estimation error is derived. Then the optimal attack strategy to maximize the identification error with the least energy is described as a min–max optimization problem with constraints.The explicit expression of the optimal attack strategy is obtained.Simulation examples are presented to verify the effectiveness of the main conclusions.

Keywords System identification·Binary-valued observations·Denial-of-service attacks·Data tampering attacks

1 Introduction

With the development of embedded technology, computer technology,and network communication technology,as well

This work was supported by the National Key Research and

Development Program of China(2018YFA0703801)and the National Natural Science Foundation of China(62173030,62033010).as the improvement of hardware system performance and data processing capabilities,cyber physical systems(CPSs)come into being to optimize system resource allocation and improve system production efficiency [1–4]. Through the communication network,CPSs exchange data between sensors and computing devices, and send the decision-making information of the computing devices to the actuators for doing the remote operation.The heavy reliance on communication networks brings new security challenges to CPSs[5–7].

In terms of the hit effect,network attacks against the Internet fall into two main categories: denial-of-service (DoS)attacks and data tampering attacks(e.g.,false data injection attacks,and data replay attacks)[8,9].DoS attacks cause data packet loss by blocking normal network services. The data tampering attack is to change system data through data modification,data injection,and data replay,thereby use wrong data to deceive the system. Therefore, when the system is subject to DoS attacks and data tampering attacks, the loss and error of data will result in a significant degradation on the accuracy of estimation and identification.

Random packet loss and periodic DoS attacks were modeled to investigate the output feedback control for CPS based on observer[10].The problem of event-triggered control was concerned for CPS under DoS attacks[11].The problem of resilient control of constrained continuous-time CPS subject to bounded disturbances and DoS attacks was studied[12].The research on data tampering attacks mainly focuses on replay attacks and data injection attacks. According to different communication frameworks [13], the data compression and compensation algorithms were proposed, and they attained the expected performance of the distributed Kalman fusion estimator (DKFE) and provided the conditions for ensuring the DKFE security under replay attacks.A periodic watermarking strategy was proposed to reduce the control cost based on creating a one-time attack duration model [14]. A dynamic attack model was proposed to characterize the typical data injection attack[15].About the problem of network security for distributed filtering under false data injection attacks, a protector was designed based on the online innovation information[16].Based on concepts originating from graph signal processing,a detection scheme was proposed for data injection attacks[17].

System with quantized observations has also been studied extensively in recent years. Guo et al. [18] introduced asymptotically efficient identification algorithms for finite impulse response systems under quantized output observations and general quantized inputs. Diao et al. [19] gave a compensation method for the packet loss deviation in system identification with event-triggered binary-valued observations. To resolve the problem of saturation-constrainted observations in the drag-free control technology, Tan et al.[20]proposed an approach of designing the adaptive control law based on set-valued identification algorithms.Risuleo et al. [21] considered the identification of linear models from quantized output data and developed a variational approximation of the likelihood function. Pouliquen et al. [22]studied the identification of infinite impulse response (IIR)systems with binary-valued measurements,where the key to our approach was to recast the initial identification problem into an identification problem in the set-membership framework. Li et al. [23] gave a novel recursive learning identification approach estimate the parameters of the Wiener systems with quantized output.

From the perspective of system identification with binaryvalued observations, this paper studies the optimal attack problem when the system is subject to both Dos attacks and data tampering attacks. Since the attack strategy is subject to energy constraints on DoS attacks,energy constraints on data tampering attacks, and constraints on the total energy,the coupling and mutual influence among these constraints significantly increase the difficulty of the optimal attack strategy problem. The packet loss rate and the data tampering rate caused by the attack is given, and the estimation error is derived. Then the optimal attack strategy to maximize the identification error with the least energy is described as a min–max optimization problem with constraints. It is interesting that the explicit expression of the optimal attack strategy is obtained.

The rest of this paper is arranged as follows. Section 2 describes the problem of system identification under DoS attacks and data tampering attacks using binary observations. Section 3 gives the min–max optimization problem of attack strategy.Section 4 establishes the optimal solution of attack strategy.Numerical examples are presented in Sect.5 to demonstrate the main results of this paper.In Sect.6,the main results of this paper are summarized and possible future research directions are briefly discussed.

2 Problem formulation

Consider a single-input single-output discrete-time system:yk= G(uk;θ)+dk,wheredkis the system noise;θis the unknown parameter;ukis the system input;ykis the system output that measured by a binary sensor with the thresholdC,which can be expressed by the following indicator function:

The system configuration is shown in Fig.1,whereskis transmittedtotheestimationcenterthroughacommunication network, but it is subject to combined attacks of DoS and data tampering.If the DoS attack occurs,the transmitted data will be lost,which can be expressed as a Bernoulli random variable:

Fig.1 System configuration

We assumeuk≡1. For other multi-parameter systems(such as linear finite impulse response systems and nonlinear Wiener systems),one can design periodic inputs to decouple themintoaseriesofgainsystemsforprocessing(moredetails see[24]).

If the estimation center does not detect the network attacks,then the optimal algorithm(in the sense of Cramér–Rao lower bound)under no attack is used to estimateθ:

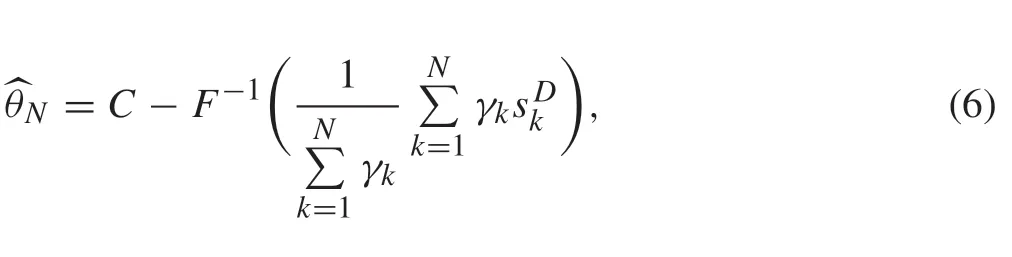
Assumption 1The system noise{dk}is a sequence of i.i.d(independent identically distributed)Gaussian random variables,and the distribution function is denoted as F(·).

3 Min-max optimization of the attack strategy

Theorem 1Consider the system(5)under the binary measurement(1)and the joint attack(p0,p1,q0,q1)of(2)–(4).If Assumptions 1 and 2 hold,then the data packet loss rate isAccording to Theorem 1,it can be seen that the total attack energy consumptionλis a function ofp0,p1,q0,q1.To show this relationship,we also writeλasλ(p0,p1,q0,q1).

Theorem 2Under the conditions of Theorem 1, the algorithm(6)under the joint attack (p0,p1,q0,q1) strongly converges to C-F-1(η),which is

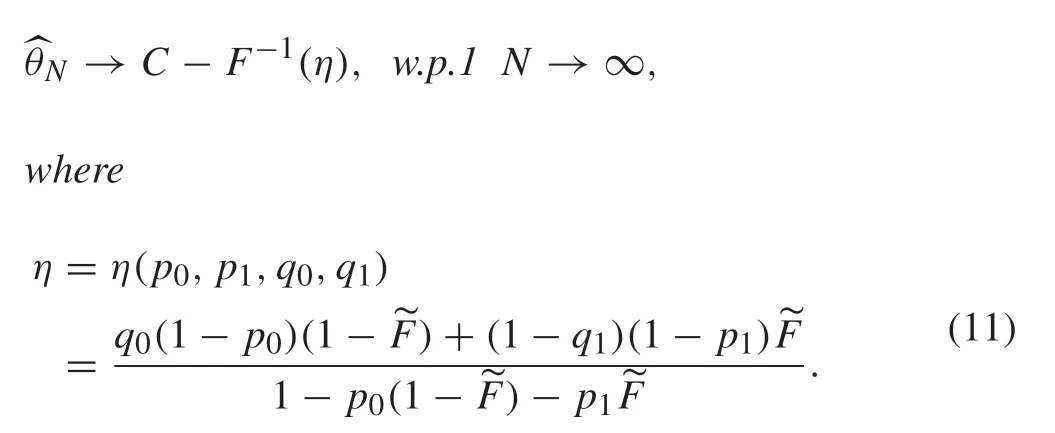
ProofBy Assumption 2 and (9),we know that{γk}is i.i.d.Thus,from the law of large numbers,one can get

4 The optimality of attack strategy

In view of Assumption 1, we know that the distribution functionF(·)increases monotonically on(-∞,+∞).Therefore,F-1(·)increases monotonically on(0,1), andζ(η)decreases monotonically on(0,1)with respect toη.According to (14), we know thatζ(η)must take the maximum or minimum value ofηwhenJ(p0,p1,q0,q1)takes

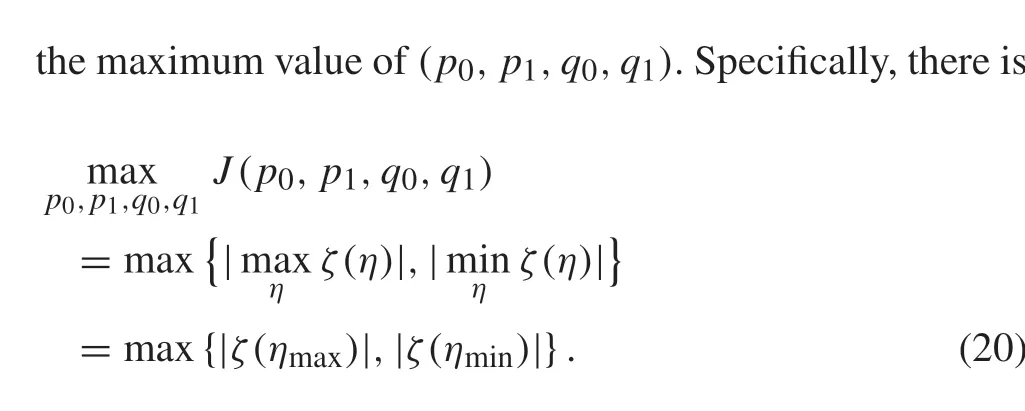
As a consequence,(20)enlightens us to seek out the minimum and maximum ofηfor solving(15)–(19).For this,some lemmas are introduced(their proofs are given in Appendix)to discuss the minimum and maximum ofη,where the following symbols are defined

Remark 2Theorem 4 illustrates what is the optimal attack strategy for different system parameters.This indicates that the optimal attack strategy depends on the system parameter.Intuitively, this makes sense. Only with a full understanding of the system,the attacker can apply the optimal attack to achieve the maximum hit effect. If the attacker does not know the system parameter,it can design an algorithm to estimate the parameter.Then the attack strategy can be adjusted according to the estimated value of the system parameter.As the parameter estimation converges to the true value,the attack strategy will converge to the optimal one as well.

5 Numerical simulation

Consider the system

Take three sets of attack strategies:two sets of non-optimal attack strategies are(0,0.2,0.1,0.1)and(0.3,0.1,0,0.1),and the other set takes the optimal attack strategy. According to the given system parameters,we have(μ1,μ2,～F,p,

In view of Figs.2 and 3,we can see that the data packet loss rate caused by the DoS attack converges to(9),and the data tampering rate caused by the data tampering attack converges to (10) under the joint attacks. Algorithm (6) converges toC-F-1(η)under the joint attacks in Fig.4.As can be seen from the Fig.5,the estimation error is largest by the optimal attack strategy under the joint attacks. These are consistent with the results in Theorems 1,2 and 4.

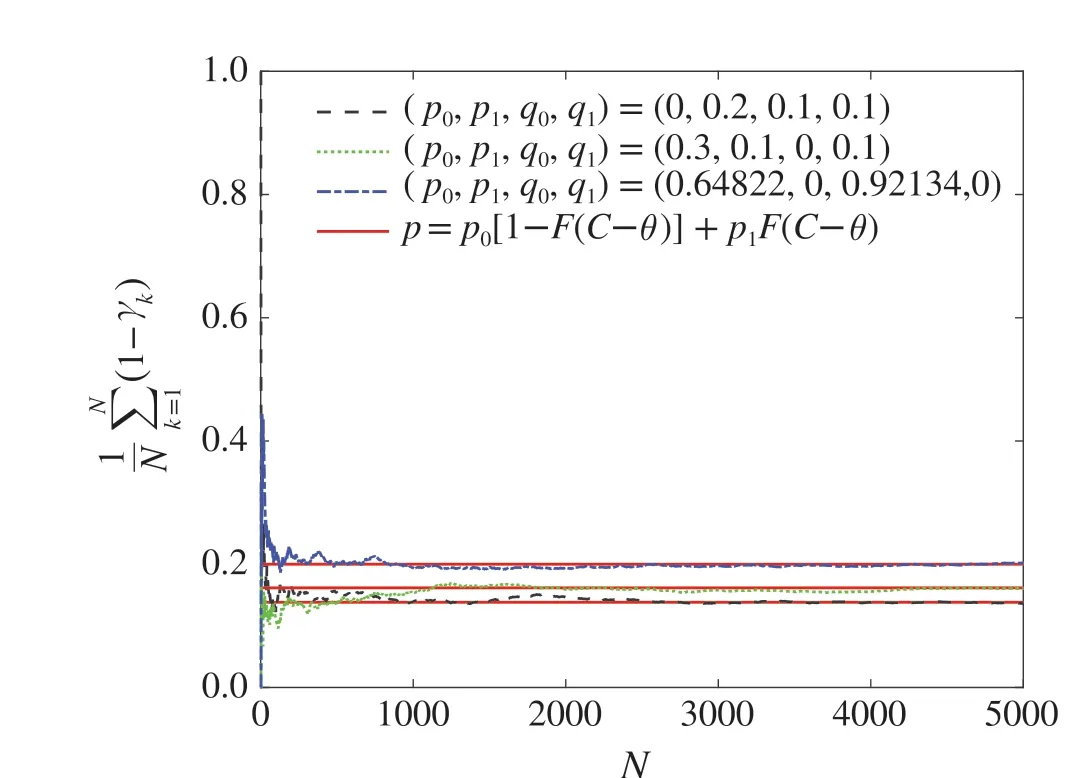
Fig.2 The convergence of data packet loss rate

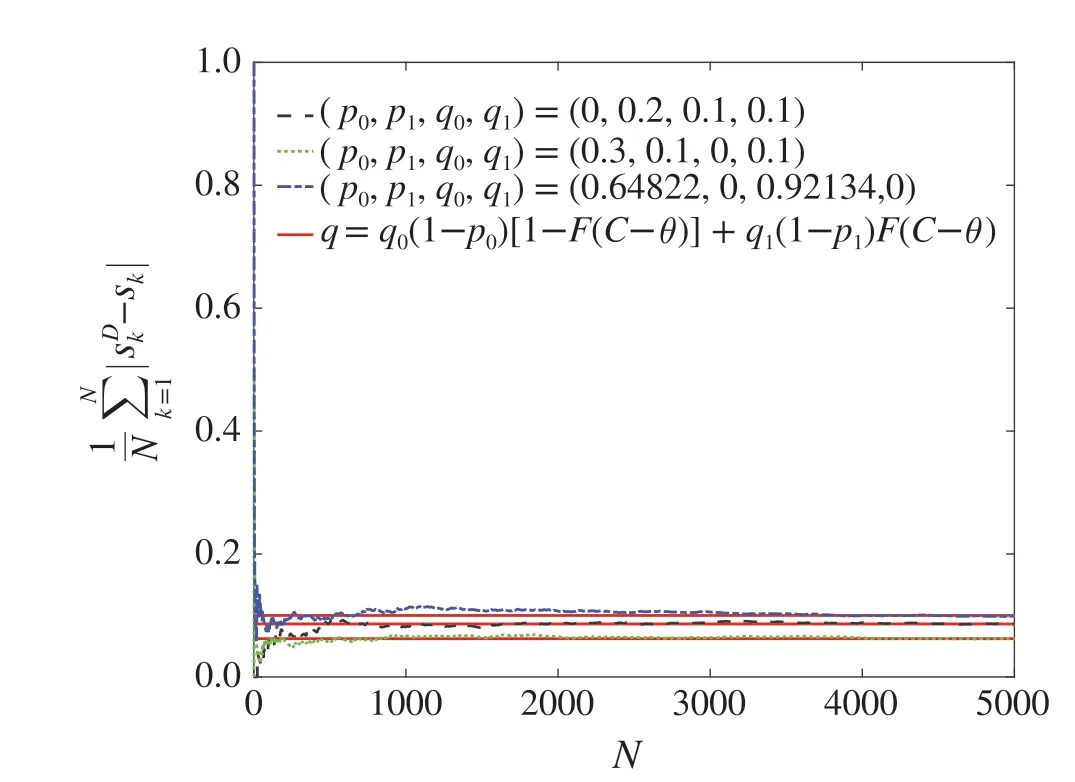
Fig.3 The convergence of data tampering rate

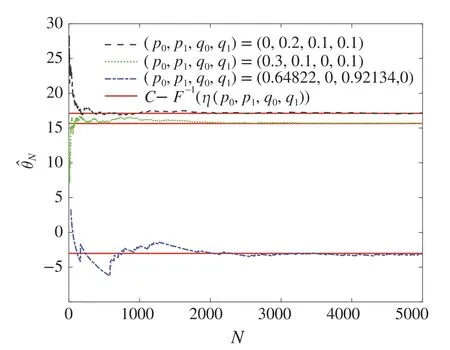
Fig.4 The convergence of Algorithm 6 under joint attacks

Fig.5 The estimated error under joint attacks

6 Concluding remarks

In this paper, we study system security issues when DoS attacks and data tampering attacks coexist from the perspective of system identification with binary-valued observations.Based on the probabilistic attack model, the optimal joint attack strategy is given in the sense of absolute estimation error subject to energy constraints.According to difference attack energies, the complete attack and incomplete attack are discussed.

Infutureresearch,theresultsofthispapercanbeexpanded to different system structures,attack models,and noise types.In addition,the defense method against the joint attack is an important and interesting research topic.

Appendix:Proof of Lemmas

Based on the above,Lemma 4 is proved.■