Suppression of high order disturbances and tracking for nonchaotic systems:a time-delayed state feedback approach

Zahed Dastan·Mahsan Tavakoli-Kakhki

Abstract Time-delayed state feedback is an easy realizable control method that generates control force by differencing the current and the delayed versions of the system states.In this paper,a new form of the time-delayed state feedback structure is introduced.Based on the proposed time-delayed state feedback method,a new robust tracking system is designed.This tracking system improves the conventional state feedback with integral action disturbance rejection characteristics in the presence of the disturbance signals imposed on the system dynamics or on the sensors that measure the system states. Also, the proposed tracking system tracks the ramp-shaped reference input signal,which is not achievable through conventional state feedback.Moreover, since the proposed method adds delays to the closed-loop system dynamics, the ordinary differential equation of the system changes to a delay differential equation with an infinite number of characteristic roots. Thus, conventional pole placement techniques cannot be used to design the time-delayed state feedback controller parameters.In this paper,the simulated annealing algorithm is used to determine the proposed control system parameters and move the unstable roots of the delay differential equation to the left half-plane.Finally,the efficiency of the proposed reference input tracker is demonstrated by presenting two numerical examples.

Keywords Time-delayed state feedback·Integral control·Disturbance rejection·Robust tracking

1 Introduction

1.1 Background

In recent years,the effects of time delays on the performance of different systems such as biological[1],economic[2,3],social[4],and engineering[5]have been widely taken into consideration. A widely accepted point of view in control engineering is that the existence of delay is always detrimental, and it undermines the stability characteristic of the system.It might be asked whether it is possible to use delays to stabilize or improve a system’s performance or not. A successful response to this question is time-delay control(TDC). This method has been primarily proposed to overcome model uncertainties[6];however,its applications can be found in other areas as well [7–9]. Furthermore, time delays can be used as time-delay filters[10]and time-delay observers[11,12].

Time-delayed feedback or time-delay auto-synchronization is another control method that incorporates delays in its structure. The main idea of using the time-delayed feedback was proposed by Pyragas to stabilize unstable oscillations in chaotic systems[13].Thereafter,this method has been extensively applied to systems with chaotic behavior,which appear in different areas such as engineering[14,15],chemistry [16,17], and medicine [18]. More detailed information about the time-delayed feedback control originally proposed by Pyragas can be found in[19].

1.2 Motivation and challenges

The vast applications of the time-delayed feedback in controlling chaotic systems have caused scientists to seek its utilityinnonchaoticsystemsaswell.Hence,thetime-delayed feedback approach has been extended to other areas. For instance, it is used as an approximation of derivative feedback and phase synchronizer[20,21].It has been shown that the time-delayed feedback can be more effective compared to the derivative feedback,since obtaining reliable measurements of the pure derivative feedback in a noisy environment is difficult [22]. In addition, a time-delayed feedback control structure can stabilize fixed points and the system steady states as well as periodic orbits[23].

Designing effective and robust tracking systems has always been an interesting area among all control systems practitioners.Accordingly,Khan et al.[24]investigated the effect of adding delays in the tracking systems.It considers tracking error as a performance criterion and shows that the existence of a delay in a feedback loop decreases the steadystate tracking error for certain types of systems. This work initiates the idea of using the time-delayed feedback,which effectively incorporates delays in its structure, to design a tracking system and investigate the resulting system properties.

Even though delays can be used in control systems effectively, by emerging delay terms in the system equations,it is laborious to find the appropriate values of the controller parameters to stabilize an unstable system. Several methods have been proposed in the literature to stabilize systems that involve delays in their equations.These methods would be classified into frequency domain tests such as matrix pencil [25] or time-domain techniques that utilize Lyapunov’s direct method[26].Interested readers may refer to [27] for a detailed discussion about these methods.In[28],a delay-dependent LMI method has been proposed to examine the stability of a delayed system.Although this method determines a delay interval in which the system can be stabilized,in most cases,designing the controller parameters through similar methods could give rise to a nonlinear matrix inequality,which obviously requires a lot of effort to solve.Frequency domain techniques mostly set a bound on the delay values for which the system is stable. However,these techniques normally do not present a direct procedure to determine the controller parameters [27]. Consequently,it would be of great importance to present a time-delayed feedback-basedcontrolmethodwhichintroducesaneffective way to find the appropriate values for the controller parameters.

1.3 Main works and contributions

The contribution of this paper is to use time-delayed feedback characteristics to improve the tracking and disturbance rejection properties of a tracking system. In this paper, a new time-delayed feedback structure is proposed to design a robust tracking system based on an integral action [29].It is proved that the proposed control structure stabilizes an unstable system and enables it to track a step/ramp reference input. Most of the proposed methods in the context of the disturbance rejection benefit from disturbance observers to eliminate the disturbance effects on the control system output[30–35].Whereas,due to the specific form of the proposed time-delayed feedback in this paper,the closed-loop system rejects higher order disturbances on the system states’measurements without employing observers effectively.Besides,it is demonstrated that the noninvasive feature of the timedelayed feedback allows it to reject ramp disturbances on the plant dynamics and track ramp reference inputs precisely.Finally,since the existing delays in the control system structure hinder the analytical solution to the design problem,it is proposed to use the simulated annealing algorithm to determine the time-delayed feedback controller parameters.This paper is organized as follows: In Sect. 2, the conventional tracking system based on state feedback with integral action is presented. The proposed tracking system is designed in Sect.3.Section4isdevotedtothemainresults.Thesimulated annealing algorithm is introduced to design the proposed system parameters in Sect.5.Section 6 demonstrates numerical examples of the proposed system, and the paper ends with conclusions drawn in Sect.7.

2 Preliminaries

State feedback with integral action is an ordinary reference tracking approach. This tracking approach eliminates the effects of the step-type disturbances on the system output,and it is almost robust against the changes in the system parameters. This tracking method has been fully described in[29].

Consider the state-space model of a controllable system as follows:

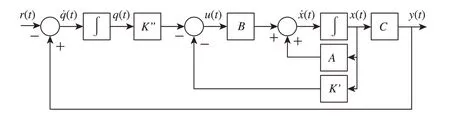
Fig.1 Block diagram of the conventional state feedback with integral action

Such a control system rejects the effect of the step-type disturbances on the system output.The block diagram of an integral control system is depicted in Fig.1.

3 Time-delayed state feedback with integral action

In this section,a tracking system is designed,benefiting from a time-delayed state feedback control structure. Using the noninvasivefeatureofthetime-delayedfeedback,theintegral stateq(t)is modified,and a condition is presented through a theorem that guarantees to track a ramp reference input by the closed-loop system.

To this end,in the conventional tracking system presented in Sect.2,consider the control signalu(t)∈Rr×1as

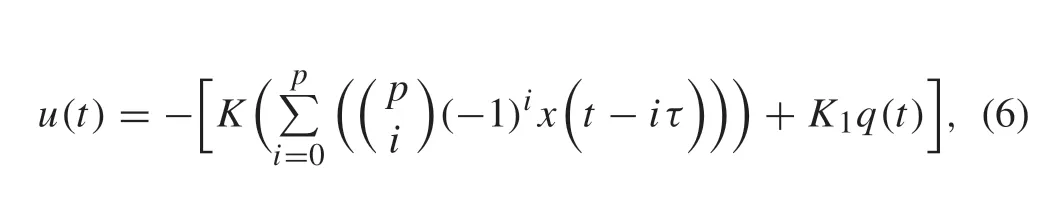
whereK∈Rr×n,K1∈Rr×mand the delayτ ＞0 is a scaler.From(3)and(6),the state-space model of the delayed augmented system is obtained as

Note that the proposed form ofu(t)in (6) preserves the noninvasive feature of the time-delayed feedback in terms of the system states.That is,whilex(t)tends to a steady state,the first term ofu(t)which directly depends on the system states vanishes.

3.1 Modification of the integral state for tracking higher order reference inputs

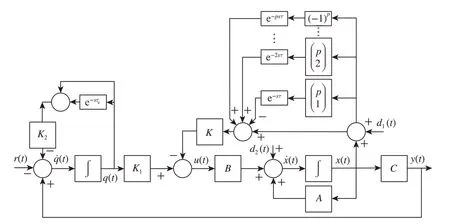
Fig.2 Block diagram of the proposed time-delayed feedback tracker with the modified form of the integral state

Accordingly, to stabilize the closed-loop system (9), the control parametersK,K1,K2,τ,τqmust be chosen,such that all of the characteristic roots of(11)lie in the left half-plane.This issue will be discussed in Sect.5 of the paper.

4 Main results

In this section, the main results of the paper are presented.First, the effect of proposed time-delayed feedback on the tracking characteristic of the closed-loop system is investigated.

4.1 Tracking properties of the proposed method

Thefollowingtheoremshowshowthetime-delayedfeedback improves the tracking properties.

Theorem 1The closed-loop system(9)tracks the step reference input.The closed-loop system(9)also tracks the ramp reference input if the equality

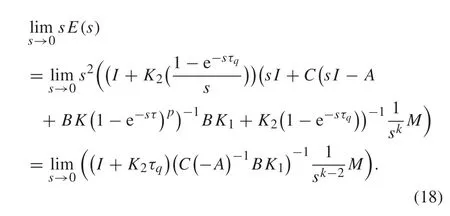
Fork= 1 (i.e., the step reference input), the tracking error vanishes asttends to infinity.Moreover,if the condition presented in(13)is fulfilled,the tracking error goes to zero fork=2(i.e.,the ramp reference input),and this completes the proof.■

Remark 1For step reference input tracking, it is not necessary to fulfill the condition presented in(13).Therefore,for the sake of design simplicity,the control parameterK2can be set to zero.

4.2 Disturbance rejection of the proposed time-delayed feedback structure

In this section, the effects of two additive external disturbancesd1(t)andd2(t)depicted in Fig.1 are discussed thoroughly.

4.2.1 Rejection of the external disturbanced1(t)

The proposed method can rejectd1(t)under the condition presented below.

Theorem 2Suppose that the closed-loop system(9)is stable for a set of the control parameters K,K1,K2,τ,τq and r(t)is a ramp/step signal.The external disturbance d1(t)affects the system states as

Theorem 3Suppose that the closed-loop system(31)is stable for a set of the control parameters K,K1,K2,τ,τq and r(t) is a ramp/step signal. Then, for d2(t)=tlV,l= 0,the tracking error goes to zero, and for l= 1, the disturbance d2(t)is rejected by the closed-loop system(31)if(20)is satisfied.

ProofTo prove this theorem, similar to the proof of Theorem 2,it is just necessary to show thatx(t)comes to zero ford2(t)/=0 andr(t)=0.

According to(31),the Laplace transform ofx(t)is given by

From (34), the steady-state value ofx(t)equals zero,which means that the ramp type disturbanced2(t)is rejected if(20)is fulfilled.It is straightforward to show that forl=0,(34)goes to zero without any condition.■

Remark 3Theorems 2 and 3 indicate that the proposed timedelayed feedback control structure proposed in this paper rejects the disturbance signald1(t)on the system states from any order.Moreover,it is robust against the step/ramp type disturbance signald2(t)on the plant dynamics. As a result,the proposed control system improves the disturbance rejection characteristic of the conventional state feedback by applying a simple time-delayed feedback method.

5 Designing procedure for the controller parameters(K,K1,K2,τ,τq)

The problem of analyzing the stability of a linear timedelayed system has been well addressed in the literature[27,37,38]. In the current case, the stabilizing problem of the closed-loop system (9) boils down to the design of the parameters of the time-delayed feedback controller for which the characteristic roots of(11)lie in the left half-plane.

Although it seems straightforward to find a set of controller parameters to place the characteristic roots of (11)in the left half-plane, to the best knowledge of the authors,there are no explicit solutions to this problem.This is because(11)is a transcendental equation with an infinite number of roots, which necessitates numerical techniques to solve the stability problem. Among the proposed numerical methods in [37,39,40] to analyze the stability of time-delayed systems, the approach presented in [39] is useful, since it has directly addressed a similar problem.The proposed method calculates the sensitivity of the m number of rightmost roots of the characteristic equation with respect to the variations of the controller parameters and continuously moves these roots to the left half-plane by applying small perturbations to the controller parameters. However, there is no theoretical proof to guarantee a global minimum or even achieving the left half-plane using this method[41].This approach was unsuccessful in stabilizing(11),possibly resulting from the fact that it got stuck in a local extremum without locating the rightmost roots in the left half-plane.

Based on [39], it is proposed to utilize an approach that moves the rightmost roots of the characteristic equation to the left half-plane.Besides,in the stabilization problem,an exact global minimum for the rightmost roots is not required.Therefore,it is sufficient to approximate the global minimum for the rightmost roots in a relatively large search space(i.e.,systems with several controller parameters).In light of these requirements, it is proposed to use the simulated annealing(SA)technique which possesses these features to tackle this problem.

The SA algorithm introduced by Kirkpatrick [42] is a probabilistic technique to approximate a global optimum of a function. This algorithm was first inspired by statistical mechanics and has been applied to several optimization problems such as the traveling salesman problem [43]. The SA algorithm has been widely discussed and used for a variety of applications [44,45]. Accordingly, the assumptions and mathematical details of the algorithm will not be discussed herein,and it is directly utilized to design the time-delayed feedback controller parameters.

To apply the SA algorithm to the current problem, an energy functionE(W)must be defined, which shows the energy of the system at the stateW. In this case,E(W)indicates the rightmost root of the characteristic (11) and the stateWis the set of the controller parameters orW≜(K,K1,K2,τ,τq). Another important element in the SA algorithm is the temperatureTwhich should be initialized appropriately for different optimization problems. Finally,the probability of accepting a state change is determined by the Boltzmann distribution of the energy difference of the two states as follows:

By these definitions,the following SA algorithm is introduced for determining the time-delayed feedback controller parametersWfor which the closed-loop system(9)is stable.

Algorithm 1 The SA algorithm for determining the proposed time-delayed feedback controller parameters.

Step 1Initializing the controller parametersWby random values.

Step 2InitializingTwith a large value.

Step 3Repeat:

1. Repeat

a. Applying random perturbation to the controller parameters asW=W+ΔW.

b. ComputingΔE=E(W+ΔW)-E(W):ifΔE ＜0,keep the new set of the controller parametersW; else, accept the new set of the controller parameters with the probabilityP= e-ΔE/Tuntil the number of the accepted changes is less than a specific threshold level.

2. SetT=T-ΔT.

This step is repeated untilTbecomes close enough to zero,orE(W)reaches the desired value,which is determined by the designer.

In this algorithm,E(W)or the rightmost root of(11)can be calculated effectively using the MATLAB package DDEBIFTOOL [46]. Notice that in each iteration,ΔWmust be chosen according to the physical constraints on the values of the controller parameter,i.e.,the delay values must be kept positive during the algorithm.Moreover,in[47],it has been shown that ifTis decreased,such that

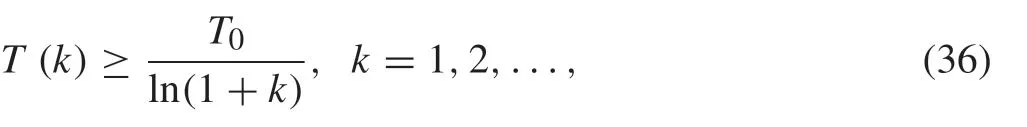
wherekindicates the iteration number andT0is a sufficiently largeinitialtemperature;theSAalgorithmwillfindtheglobal optimum with probability value one.

The design flowchart of the proposed approach is presented in Fig.3.

6 Simulation results

In this section,at first,two numerical examples are provided to show the efficiency of the proposed control approach in reference tracking and disturbance rejection.Then,the proposed approach is compared to a robust H∞controller.

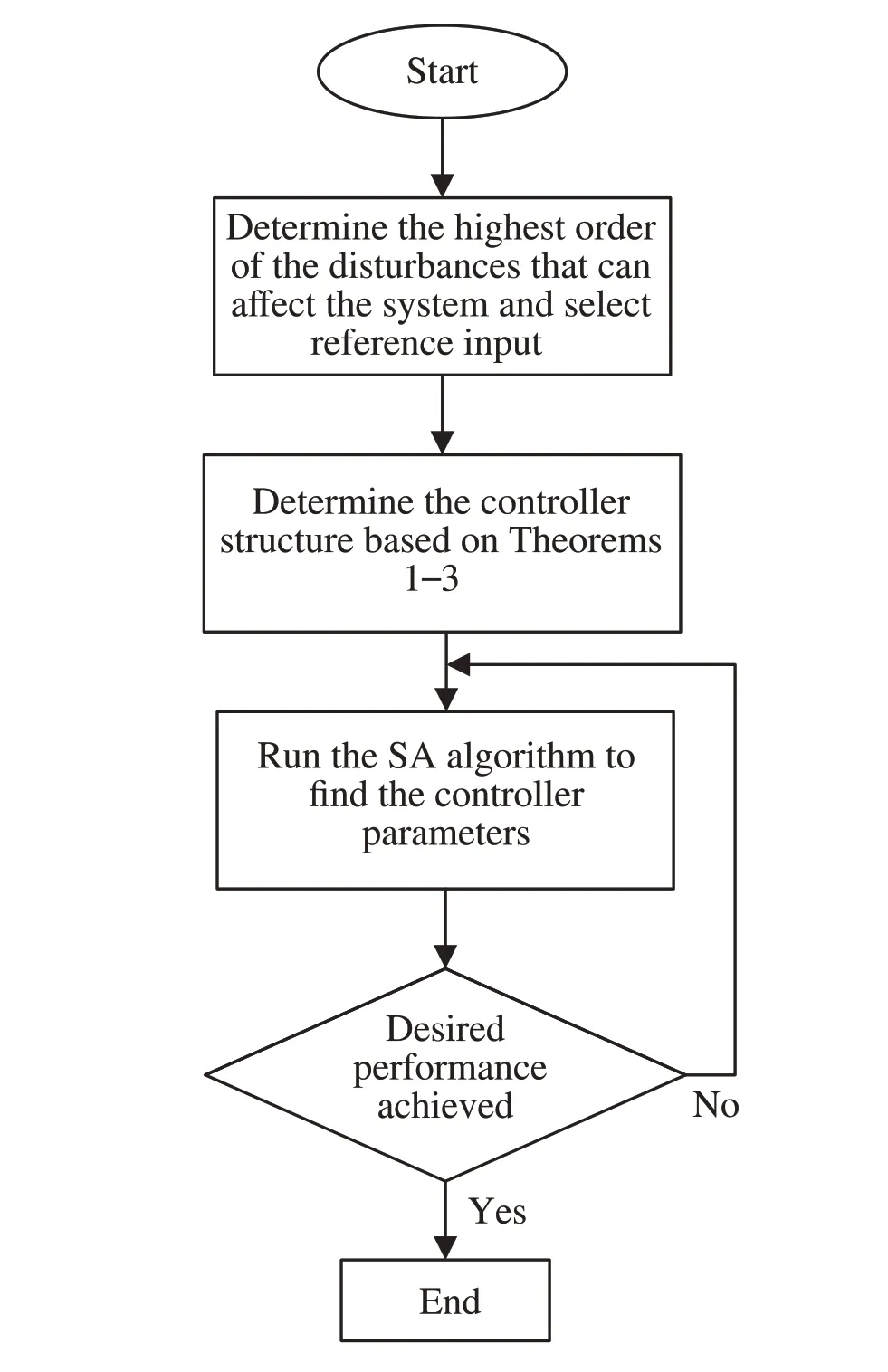
Fig.3 Design flowchart for the proposed time-delayed feedback tracking system

6.1 Case studies

Consideringu(t)in(6)forp=1 and the integral state as(8)forτq=0,theSAalgorithmisusedtofindtheappropriate values of the controller parametersK=[k1k2],K1=k11andτin (6). Figure4a indicates the time-delayed feedback controller parameters with respect to the iteration number of the SA algorithm. Furthermore, Fig.4b shows the real part of the rightmost root of the characteristic (11) with respect to the iteration number in the SA algorithm.

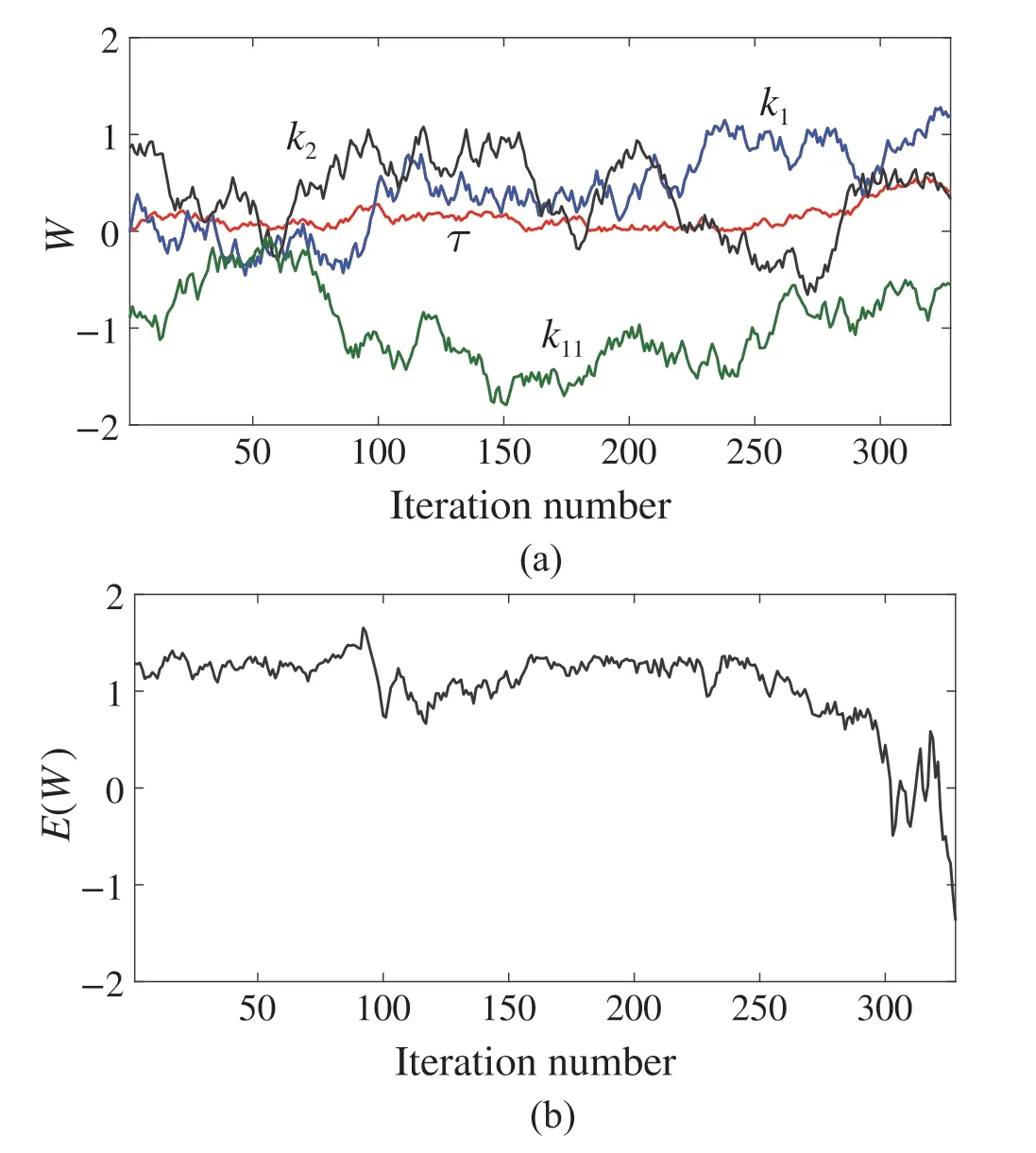
Fig.4 Designing the time-delayed feedback controller parameters with the SA algorithm for Example 1. a Time-delayed feedback controller parameters K =[k1 k2], K1 =k11,and τ with respect to the iteration number of the SA algorithm for p = 1 and τq = 0.b The real part of the rightmost root of the characteristic equation(11)with respect to the iteration number of the SA algorithm for p =1 and τq =0

whereH(·)is the unit step function.This signal is demonstrated in Fig.5a.

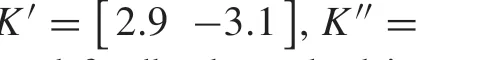
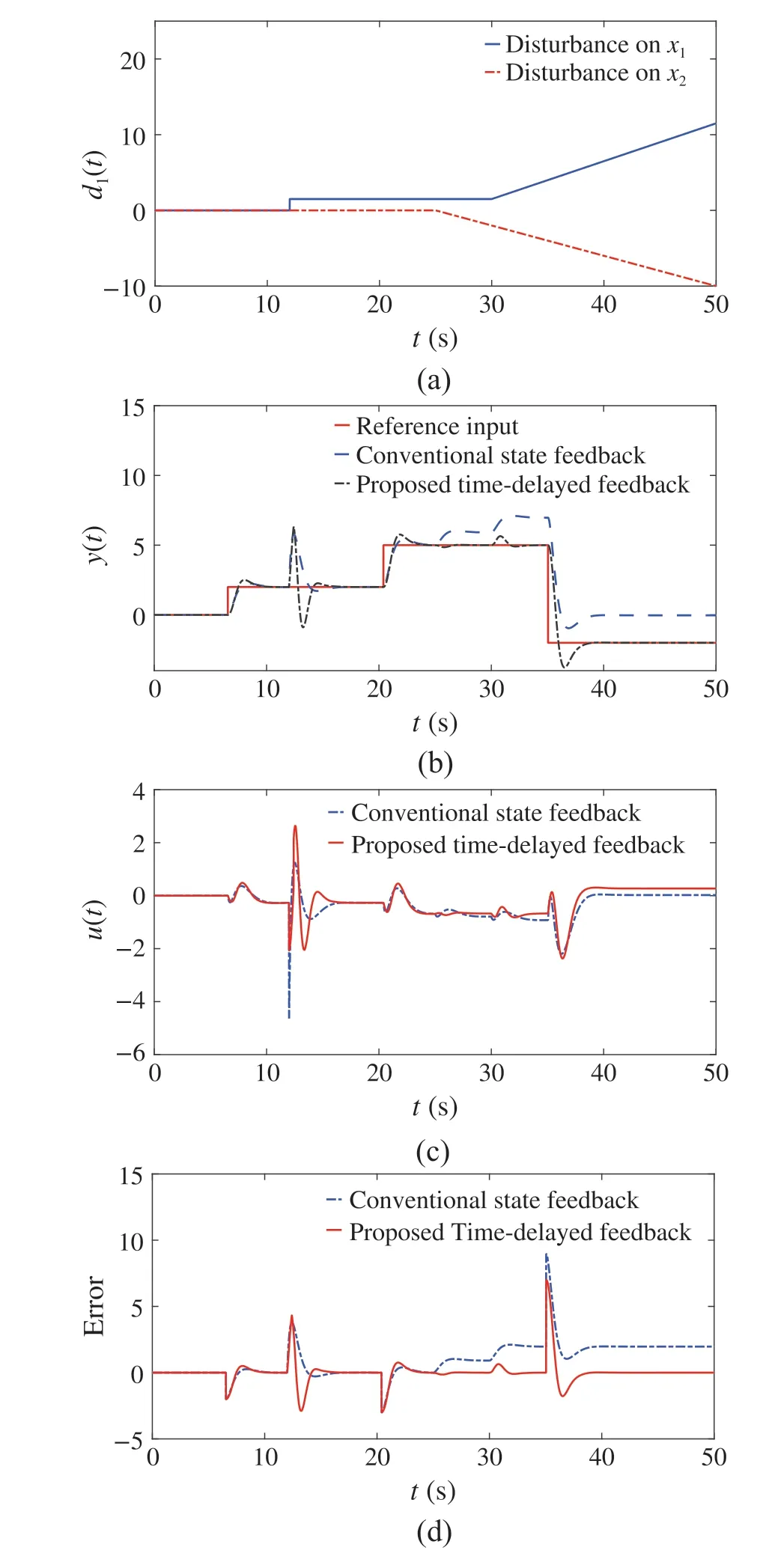
Fig.5 The corresponding signals of the proposed time-delayed feedback with p = 1 and τq = 0 and the conventional state feedback with the step reference input.a Disturbance signal d1(t)imposed on the system states x1(t) and x2(t). b Comparison of the closed-loop system outputs by applying the conventional state feedback and the proposed time-delayed feedback method in the presence of the disturbance signal d1(t) in Fig.5a. c Control signal u(t) corresponding to Fig.5b. d Tracking error signals corresponding to Fig.5b

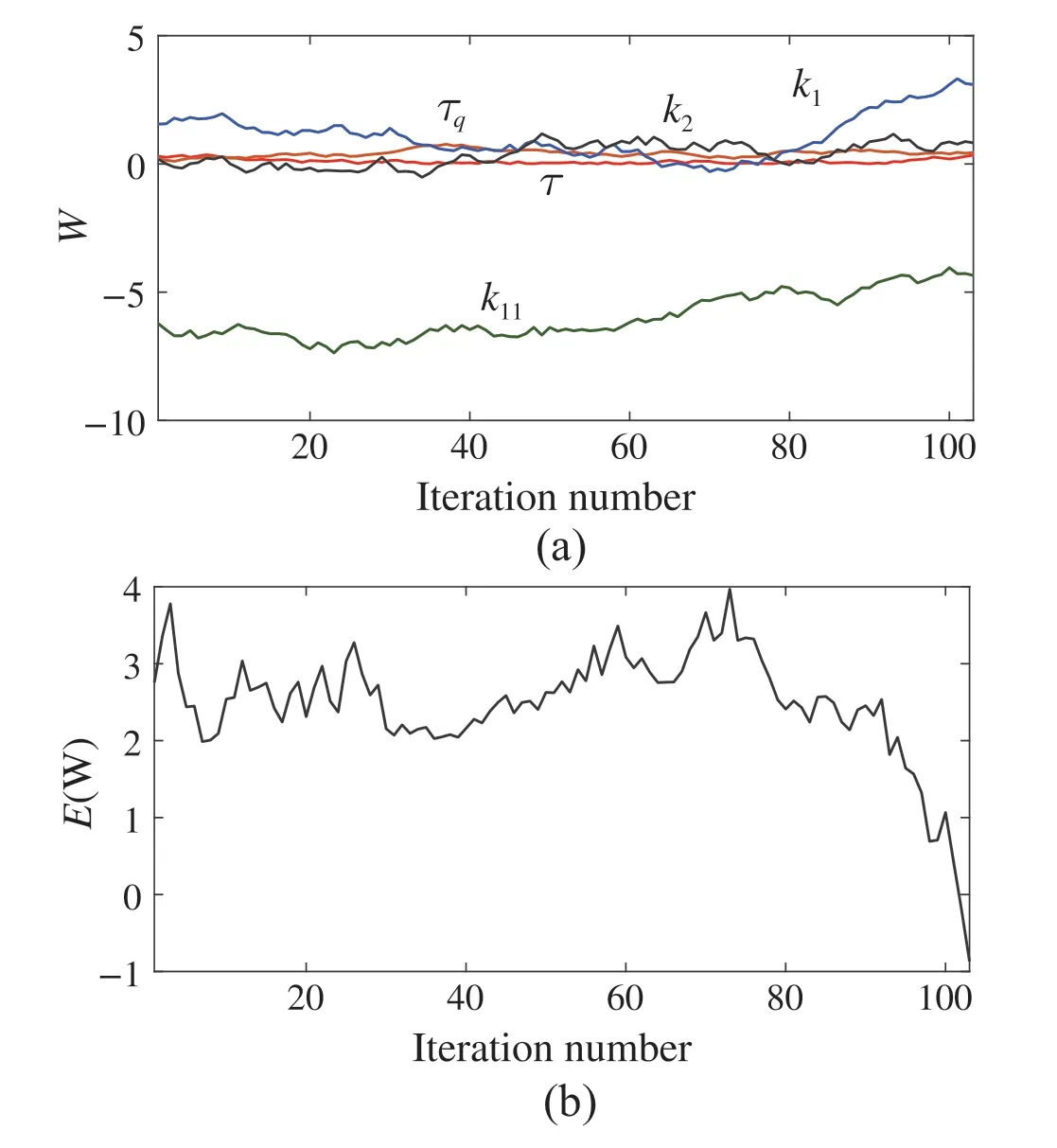
Fig.6 Designing the time-delayed feedback controller parameters with the SA algorithm.a Time-delayed feedback controller parameters K =[[k1 k2], K1 = k11, τ and τq with respect to the iteration number of the SA algorithm for p = 1 and τq /= 0. b The rightmost root of the characteristic equation(11)with respect to the iteration number of the SA algorithm for p =1 and τq /=0

Based on Theorem 2 and Theorem 3, these configurations should permit the closed-loop system to rejectd1(t)=tl1V,l1= 0,1,2, andd2(t)=tl2V,l2= 0,1. Hence,d2is selected to be a time-shifted version of(37),andd1(t)is given by

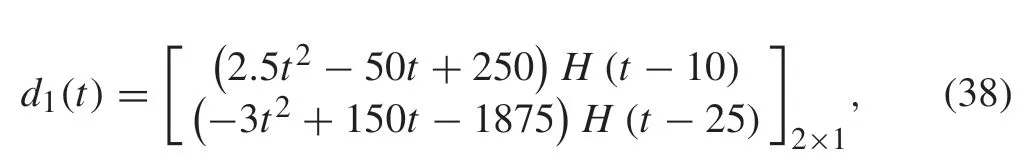
which is a combination of parabolic,ramp,and step signals.Figure7a,billustratesthedisturbancesignalsd1(t)andd2(t),respectively.

The closed-loop system output by applying the proposed time-delayed feedback method in the presence of the simultaneous disturbance signalsd1(t)andd2(t)is represented in Fig.8a.In addition,Fig.8b implies that under these circumstances,the control signalu(t)of the proposed time-delayed feedback remains bounded.

Also,the tracking error of the proposed control system in this condition is depicted in Fig.8c. As seen, the proposed time-delayed feedback control system tracks the reference input signal and rejects both disturbances in the steady state withoutanyerror,whichconfirmtheresultsofTheorem2and Theorem3.Moreover,Fig.8dillustratesthattheconventional state feedback method is unable to track the reference input in the presence of the same disturbance signals. Therefore,the other corresponding signals have not been compared in this case.

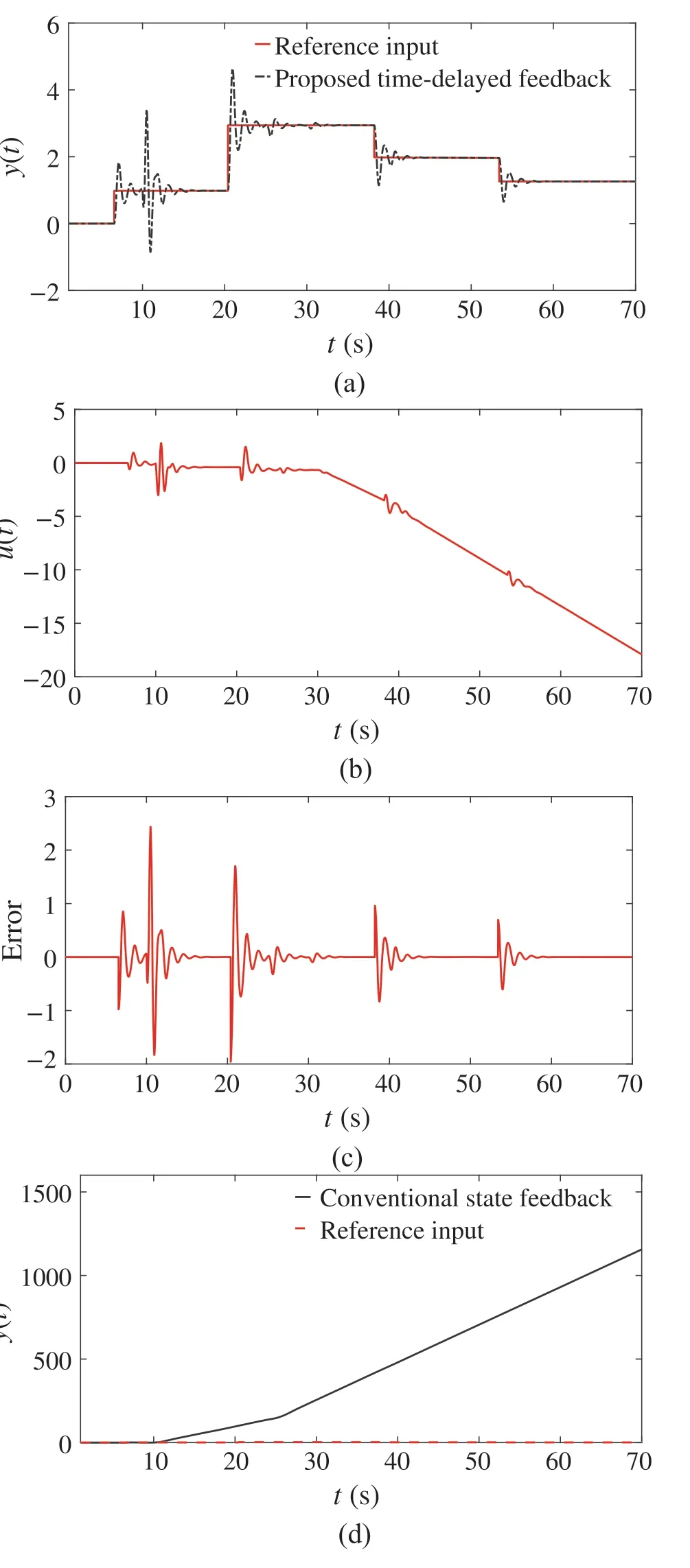
Fig.8 The corresponding signals of the proposed time-delayed feedback with p = 1 and τq /= 0 and the conventional state feedback output with the step reference input.a Closed-loop system output with the proposed time-delayed feedback in the presence of the simultaneous disturbance signals d1(t)in Fig.7a and d2(t)in Fig.7b.b Control signal u(t)corresponding to Fig.8a.c The tracking error signal corresponding to Fig.8a.d Closed-loop system output with the conventional state feedback in the presence of the simultaneous disturbance signals d1(t)in Fig.7a and d2(t)in Fig.7b

To check Theorem 1 results, a combination of step and ramp reference inputs along with disturbancesd1(t)andd2(t)illustrated in Fig.7a and b are imposed on the system. Figure9a shows the reference input tracking of the designed control system under these circumstances. Likewise,As seen from Fig.9b,the control signalu(t)is bounded.Also, the tracking error under these circumstances is presented in Fig.9c. As it has been described in Sect. 4 and it is shown in Fig.9a–c, this complex combination of the reference inputs and the external disturbances can also be effectively handled by the design control system based on the time-delayed feedback method.Moreover,Fig.9d shows that these circumstances cannot be handled by the conventional state feedback method.

Example 2The longitudinal short mode of an aircraft in the first operating point can be described by a third-order linear system[48]

whereNzrepresents the normal acceleration,qis the pitch rate,andδerepresents the elevator angle.Three eigenvalues are -3.0686,1.2278,-30, which means that the system is unstable.

Similar to Example 1,the time-delayed feedback control signalu(t)in (6) is considered withp= 1,τq/= 0. Furthermore, by assumingK2= -1/τq, the conditions given in (13) and (20) are fulfilled. The SA algorithm is used to obtain the controller parameters.Figure10a,b demonstrates thecontrollerparametersandtherightmostrootofthecharacteristic(11)versus the iteration number of the SA algorithm,respectively.

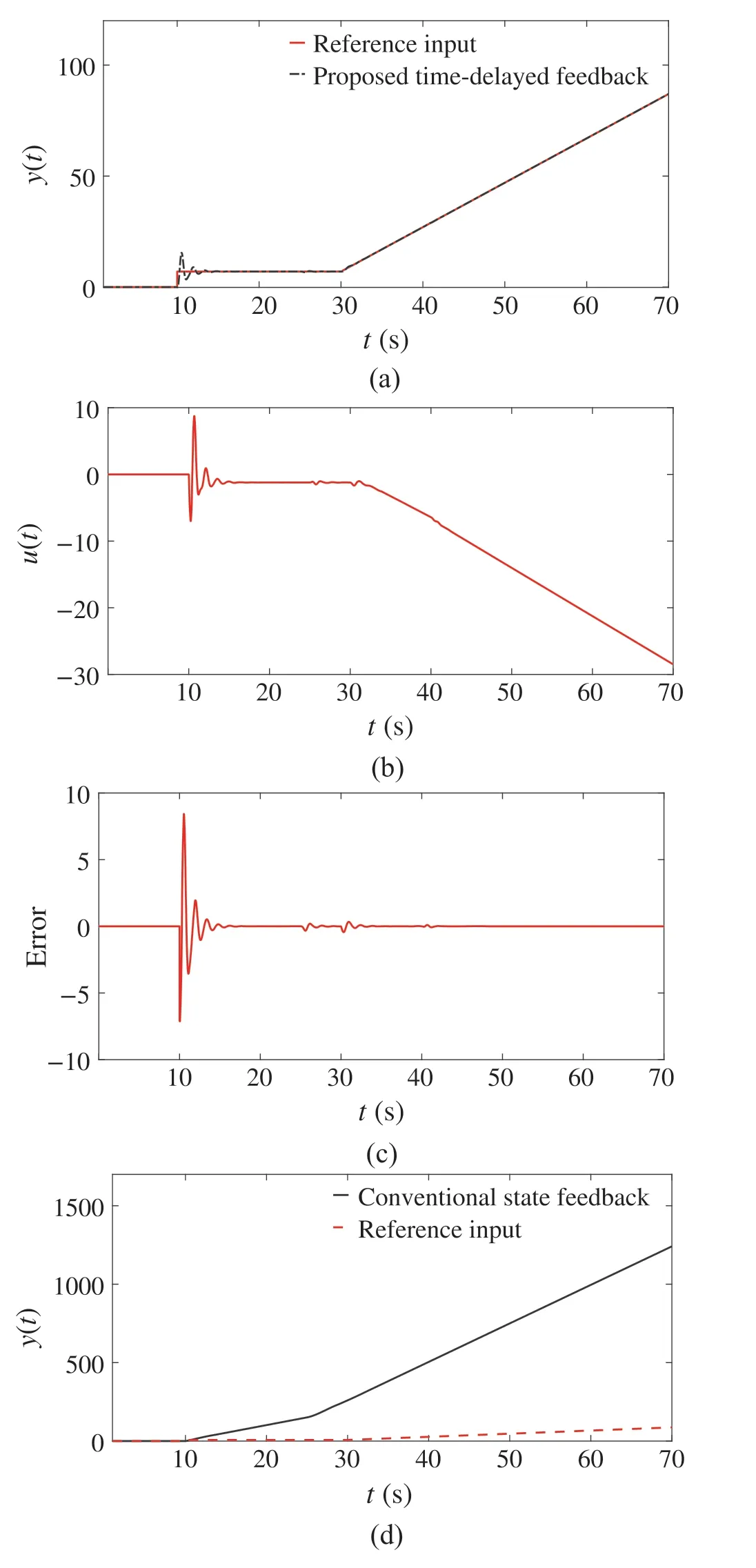
Fig.9 The corresponding signals of the proposed time-delayed feedback with p =1 and τq /=0 and the conventional state feedback output with a combination of ramp and step reference input a closed-loop system output with the proposed time-delayed feedback by applying step and ramp reference inputs and in the presence of the simultaneous disturbance signals d1(t)in Fig.7a and d2(t)in Fig.7b.b Control signal u(t)corresponding to Fig.9a.c The tracking error signal corresponding to Fig.9a.d Closed-loop system output with the conventional state feedback by applying step and ramp reference inputs and in the presence of the simultaneous external disturbances d1(t)in Fig.7a and d2(t)in Fig.7b

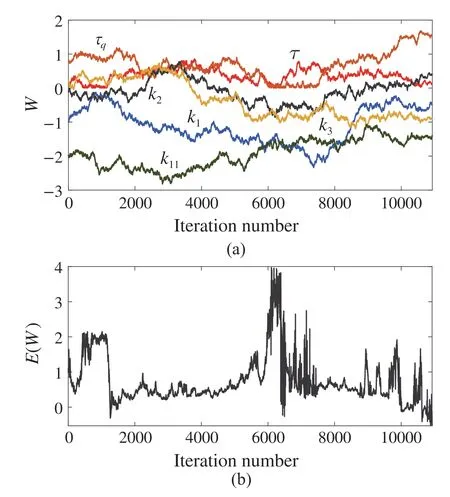
Fig. 10 Designing the time-delayed feedback controller parameters with the SA algorithm for Example 2.a Time-delayed feedback parameters K =[k1 k2 k3],K1 =k11,τ and τq with respect to the iteration number of the SA algorithm for p = 1 and τq /= 0.b The real part of the rightmost root of the characteristic equation(11)with respect to the iteration number of the SA algorithm for p =1 and τq /=0

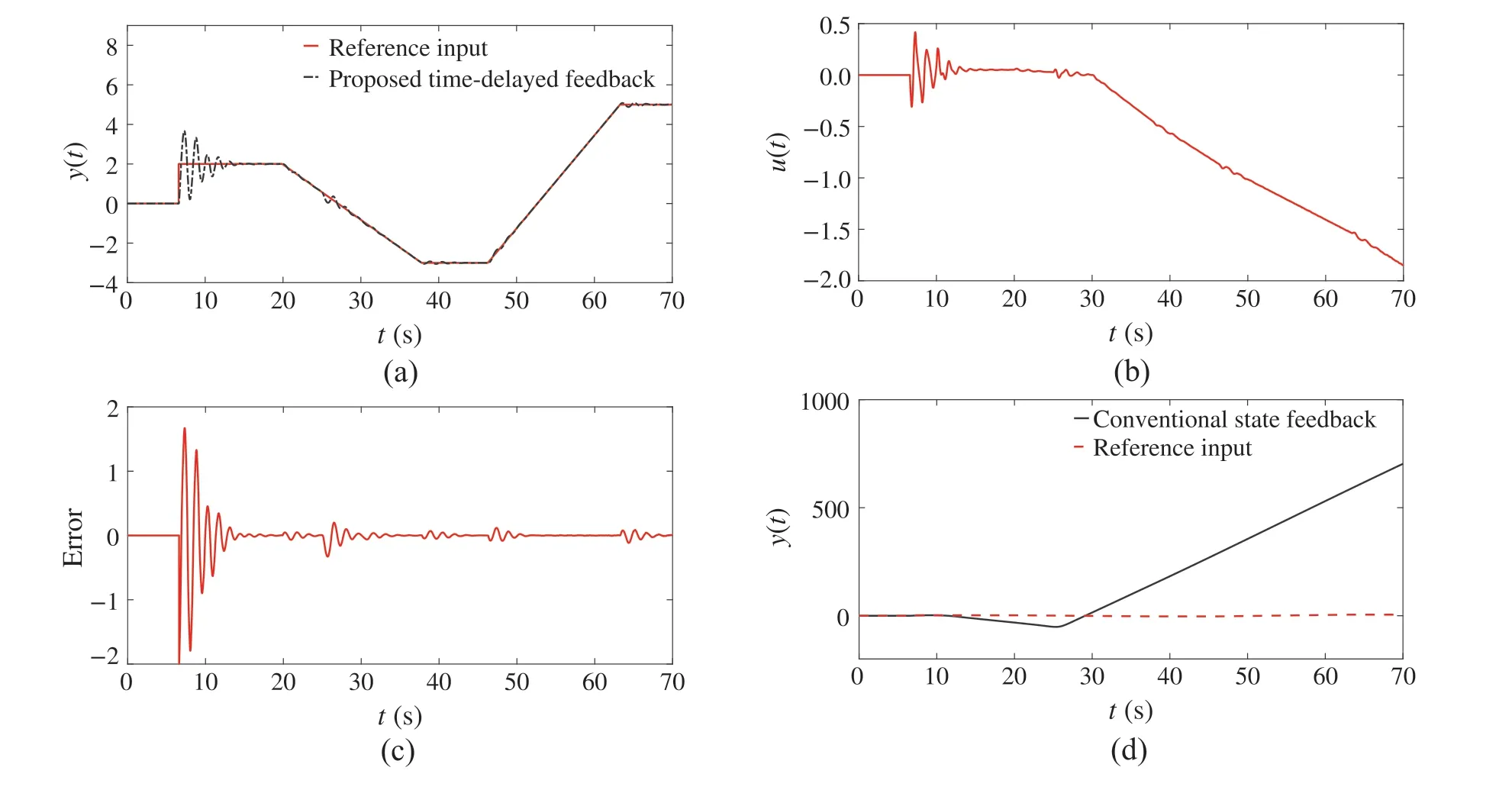
Fig.11 The corresponding signals of the proposed time-delayed feedback for Example 2 with p =1 and τq /=0 and the conventional state feedback output with a combination of ramp and step reference input a closed-loop system output with the proposed time-delayed feedback by applying step and ramp reference inputs and in the presence of the simultaneous disturbance signals d1(t)in Fig.7a and d2(t)in Fig.7b.b control signal u(t)corresponding to Fig.11a.c the tracking error corresponding to Fig.11a.d closed-loop system output with the conventional state feedback by applying step and ramp reference inputs and in the presence of the simultaneous disturbance signals d1(t) in Fig.7a and d2(t)in Fig.7b

For the sake of brevity, a combination of step and ramp signals is considered as an input signal.Moreover,the external disturbancesd1(t)andd2(t)indicated by Fig.7a and b are applied. Figure11a demonstrates the proposed control system output for the input reference signal and confirms the closed-loop system’s ability to track this signal without any error.This fact is shown in Fig.11c,which implies that the steady-state tracking error goes to zero. It is helpful to assess the control input amplitude during the system operation.Figure11bshowsthatthecontrolinputremainsbounded throughout the time,which signifies the proposed method’s efficacy.Finally,Fig.11dindicatesthatunderthesamecondition,the conventional method is unable to track the reference input.

6.2 Comparing performance with robust H∞controller

It is instructive to compare the proposed time-delayed feedback tracking system with one of the most common forms of feedback,namely,the PID controller.Figure12 illustrates the block diagram of the tracking system using a PID controller.In this section,we tune the PID controller parameters to minimize the effect of disturbances on the tracking error using the MATLAB Robust Control Toolbox.To achieve this,we first convert the block diagram shown in Fig.12 to the standard configuration illustrated by Fig.13.In this figure,the exoge-

Fig.12 Block diagram of the tracking system based on the robust H∞controller C(s)in(40)

Fig.13 Standard configuration for robust H∞controller design

Figure14a shows the robust H∞controllerC(s)in (40)and proposed method outputs under the influence ofd2(t)shown in Fig.7b.It can be seen that the robust H∞controller has less oscillations in the beginning.However,the tracking error in Fig.14b reveals that the robust H∞controller tracks the reference input with a steady-state error, whereas the proposed time-delayed feedback tracks the reference input precisely.

In summary, Table 1 shows how the proposed timedelayed feedback improves the tracking and disturbance rejection properties of the conventional state feedback tracking system.

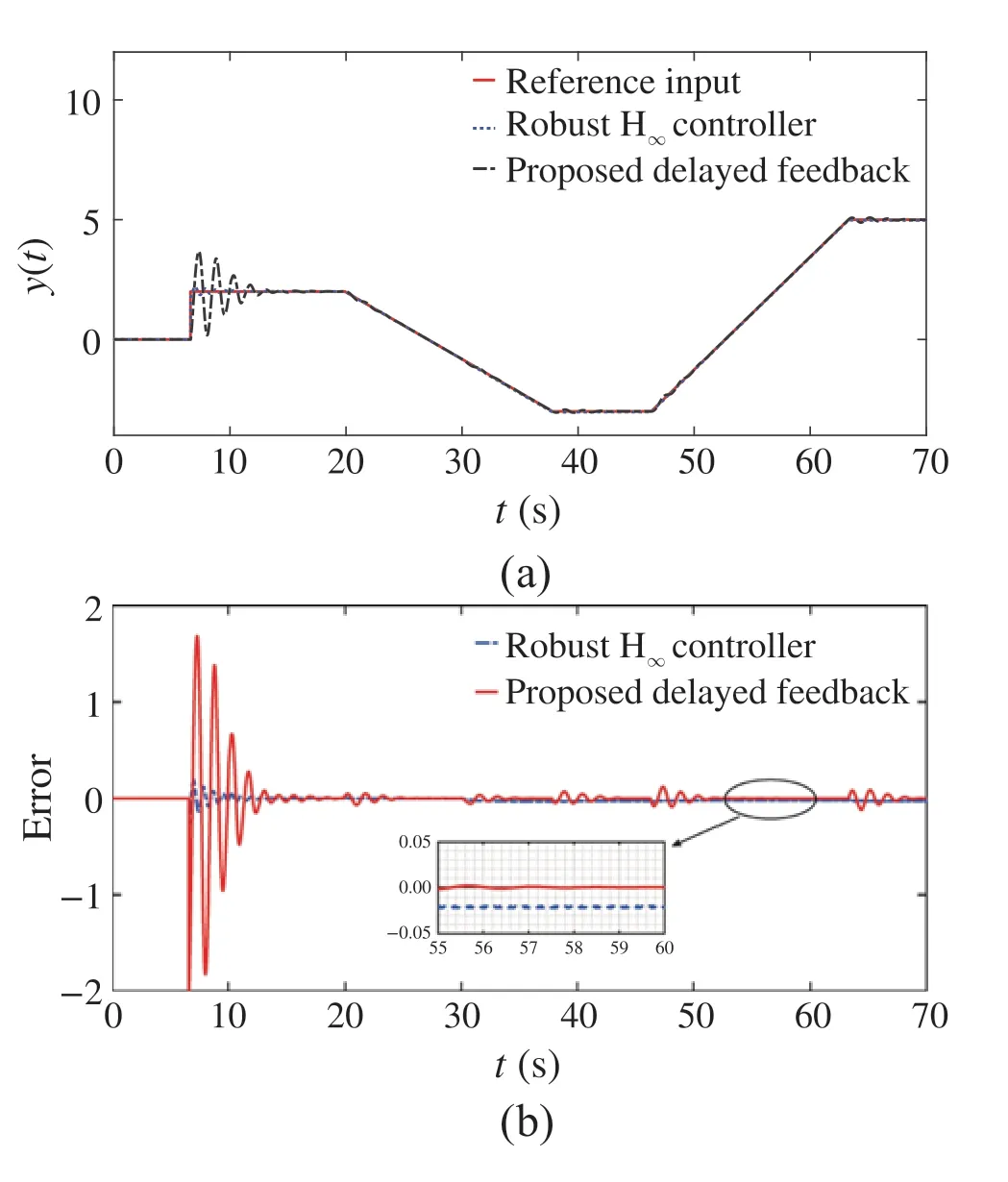
Fig.14 The corresponding signals of the proposed time-delayed feedback for Example 2 with p =1 and τq /=0 and the robust H∞controller output with a combination of ramp and step reference input a comparison of the closed-loop system outputs by applying step and ramp reference inputs in the presence of disturbance signal d2(t)in Fig.7b.b The tracking error corresponding to Fig.14a

7 Conclusions

In this study, the conventional integral action tracking method has been improved by the time-delayed feedback control scheme. The proposed method stabilizes the conventional integral action tracking system using the timedelayed feedback. Hence, it integrates the time-delayedfeedback features with the conventional tracking system structure.Because of the time-delayed feedback characteristics,the proposed method rejects higher order disturbances.Besides, based on the noninvasive feature of the timedelayed feedback, a new term is added to the integral state, which increases the closed-loop system disturbance rejection property by one order. Moreover, by satisfying a simple condition,this new term will enable the closed-loop system to track step/ramp reference input signals.The proposed system possesses a convenient implementation feature which makes it a suitable choice for most practical applications.

Table 1 Comparison between the tracking error of the proposed time-delayed feedback(eD(t))and the conventional state feedback(eS(t))tracking methods for different types of external disturbances d1(t),d2(t)and the reference input r(t)